同構法在解題中的應用淺析
?安徽省滁州中學 葉建友?廣西南寧市銀海三雅學校 林日官
1 引言
近幾年高考和各類模擬題中頻頻出現“同構”的身影,即通過構造相同的形式,根據相同的格式“脫掉”復雜形式的外殼,露出問題的本質,或是萬象歸一,化歸為更統一的規律,體現數學的對稱美,具有一定的美學價值.
2 函數與導數中的同構方法
核心素養下的數學教育更注重數學的內在美與本質的體現,在學習的過程中學生既能夠明白相關的數學原理與應用,還能體會到數學中的美,新高考更是在這個方面下足了功夫.我們來看下面幾道高考題.
2.1 利用同構獲取變元的大小關系
例1(2020年全國Ⅱ卷文理)若2x-2y<3-x-3-y,則( ).
A.ln(y-x+1)>0 B.ln(y-x+1)<0
C.ln|x-y|>0 D.ln|x-y|<0
分析:題目中給出的條件為關于兩個變元x,y的不等式,直接獲得關于y-x的式子并不容易,所以可以考慮構造相同的形式,即由2x-2y<3-x-3-y,得2x-3-x<2y-3-y,不等號兩端的形式完全一致,只是對應的變量不同而已,達成了同構.構造函數f(t)=2t-3-t,易知該函數為R上的增函數,由增函數的特點可知x
規律總結:數學中有許多形式對稱優美的式子,它們遍布在數學的各種定義和性質當中,猶如數學中的瑰寶,給人美不勝收的感覺.在上面的問題中,我們構造函數,知曉了該函數的單調性,從而根據單調性的特點解決了問題.所以這類問題的理論依據是函數的單調性的特點,根據單調性和函數值的大小得到了自變量的大小關系,相當于脫掉了函數對應關系的外殼,直接獲得兩個變量的大小關系,從而能夠更簡潔地還原問題本質,簡單地解決問題.
熟練應用:
例2(2020全國Ⅰ卷理)若2a+log2a=4b+2log4b,則( ).
A.a>2bB.a<2b
C.a>b2D.a 分析:根據題意可將已知條件整理為2a+log2a=4b+2log4b=22b+log2(2b)-1的形式,則可構造函數f(x)=2x+log2x,易知f(x)為區間(0,+∞)上的增函數,而f(a)=f(2b)-1 在我們遇到的問題當中,有時不一定一眼就能看出要構造的函數的形式,而是需要通過變形整理再找到要構造的函數,這樣的問題對我們知識的掌握要求較高,更能體現我們對一些數學問題理解的深度,所以構造才是數學魅力的地方之一,有時可以借助于同構獲取變元的關系來解決一些取值或不等式的相關問題. 例3解不等式log2(x12+3x10+5x8+3x6+1)>1+log2(x4+1). 例4已知實數x1,x2滿足x1ex1=e3,x2(lnx2-2)=e5,則x1x2的值為________. 分析:本題中涉及兩個變量,各自滿足一個對應的方程,涉及到指數與對數的運算,所以一個角度是采用換元的方式.由于方程首先需要有意義,所以有x1>0,x2>e2.令lnx2-2=t>0,x2=et+2,則第二個方程化為tet=e3.構造函數f(x)=xex(x>0),f′(x)=(x+1)ex>0(x>0),則知f(x)在區間(0,+∞)上單調遞增.而f(x1)=f(t)=e3,則x1=t=lnx2-2,所以x1x2=x2(lnx2-2)=e5. 另一個角度就是化同構,對第一個方程x1ex1=e3兩邊取自然對數,得lnx1+x1=3. 對第二個方程x2(lnx2-2)=e5兩邊取自然對數,得lnx2+ln(lnx2-2)=5. 為使兩式結構相同,將上式進一步變形為(lnx2-2)+ln(lnx2-2)=3. 構造f(x)=lnx+x,易知f(x)在區間(0,+∞)上單調遞增,則f(x)=3的解只有一個.所以x1=lnx2-2,因此x1x2=(lnx2-2)x2=e5. 除了能夠根據同構直接獲得變元的大小關系外,有時也可以利用同構間接地解決恒成立、參數范圍等問題,應用比較廣泛. 合并前,兩館都使用《中國圖書館分類法》,但在各自的分編工作中,兩館的分類規則有差別,導致索書號不同,南館圖書使用的索書號是用著者號排序,北館則使用種次號排序。這兩種不同的排序法會造成讀者從北館借閱的書還到南館后上不了架。由于索書號的取號法、館藏標記符號等方面存在差異,如何將讀者所借的北館上萬冊圖書歸入南館分類排架系統中,是合并后圖書館所面臨的一個迫切任務。 該題將題中復雜的條件同構處理后相當于知道所構造函數的單調性,再利用導數值取值情況來獲取參數的范圍. 例6(2020山東新高考)已知函數f(x)=aex-1-lnx+lna.若f(x)≥1,求a的取值范圍. 分析:本題若直接帶參討論,即使用常規處理方法會比較麻煩,而考慮同構處理則會大大簡化解題流程,提高效率.由題意知aex-1-lnx+lna≥1,即ex+lna-1+lna-1≥lnx,亦即ex+lna-1+x+lna-1≥x+lnx=lnx+elnx.構造新函數g(x)=x+ex,易知該函數在R上單調遞增,則有x+lna-1≥lnx,即lna≥-x+1+lnx.令h(x)=-x+1+lnx,可知其最大值為h(1)=0,所以有lna≥0,因此a≥1. 下面給出同構的一些經典方案: (1)基本型: (3)和差型:ea±a>b±lnb. ①可變形為ea±a>elnb±lnb,構造函數f(x)=ex±x; ②也可變形為ea±lnea>b±lnb,構造函數f(x)=x±lnx. (4)積型:aea≤blnb. ①變形為ealnea≤blnb,構造函數f(x)=xlnx,即有f(ea)≤f(b); ②變形為aea≤(lnb)elnb,構造函數f(x)=xex,即有f(a)≤f(lnb); ③兩邊取對數:a+lna≤lnb+ln(lnb),構造函數f(x)=x+lnx,即有f(a)≤f(lnb). ③兩邊取對數變形為a-lna≤lnb-ln(lnb),構造函數f(x)=x-lnx,即有f(a)≤f(lnb). 同步練習: 練習3:已知對于任意的實數m,n,不等式kmen-1-2n+1+(2n-2m+1)e2n-m≥0恒成立,則實數k的取值范圍為________. 數學核心素養的培養與落實往往需要很多具體的材料與媒介,同構的思想就是較好的媒介之一.學生對同構的認知與應用體現了對數學相關概念與思想的理解深度,這也是同構相關的試題越來越多的原因之一.學生需要具有相關的學科視角和對應的學科思想,這是我們當前教育的主旋律,也就是更需要學生能夠從整體上認識與把握相關學科,進而在細節的完善中成為一個發展完整的人,才能達成我們的教育目標.函數中的同構聯結了其形式與內在的統一,自變量與函數值的依存關系通過同構的轉化體現得淋漓盡致,不僅有數學思想的深刻性,也給人以美的感受,是更高的科學追求.當然,同構的思想在其他領域,如解析幾何的相關運算中也有很多應用,亟待我們繼續發掘和探索.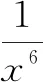
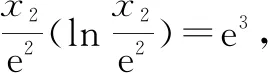
2.2 利用同構求參數的取值范圍
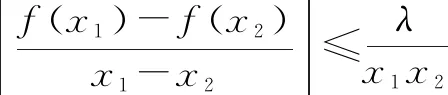
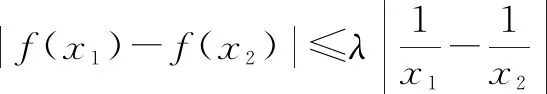
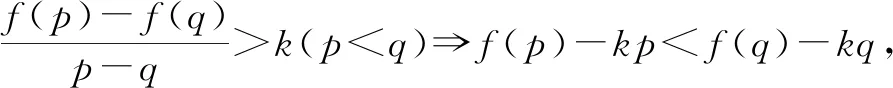

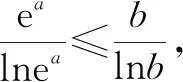
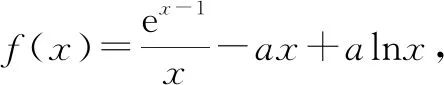
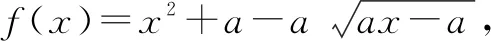
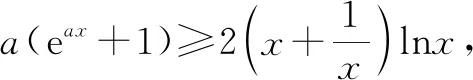
3 結束語

