例談解析幾何中的定值問題
?福建省莆田第六中學 蘇雪晶
1 引言
定值問題和定點問題是解析幾何高考題中的熱點題型.本研究重點探究定值問題中如何轉化,優化運算,提高解題效率等問題.定值問題一般涉及與曲線上的動點、線系等有關的定值問題以及與圓錐曲線有關的弦長、面積、橫(縱)坐標、長度比值,掌握了定值求值規律和技巧,會更好地解決這一類問題,做到由此及彼、觸類旁通.
2 定值問題題型分析
解題過程中,要總結解題方法,理解解題策略,通過有效的方法來分析,達到掌握通性通法,面對相關問題都可以輕松應對.在解題時要引入核心變量,將所求表達式用核心變量表示,通過推理、計算,消去變量,從而得到定值.定值的確定是解題的根本,也是解題的最終目標.當然實踐是檢驗真理的唯一標準,我們要深入掌握這類題型的解題方法,必須勤加練習,積累解題經驗,優化解題過程,不斷調整解題策略,下面讓我們通過幾個典型例題來小試牛刀.
2.1 題型一:斜率定值問題
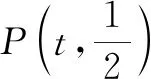
(1)求拋物線C的方程;
(2)拋物線C上一點A的縱坐標為1,過點Q(3,-1)的直線與拋物線C交于M,N兩個不同的點(均與點A不重合),設直線AM,AN的斜率分別為k1,k2,求證:k1k2為定值.
解析:(1)拋物線C的方程為y2=x.(過程略)
(2)因為點A在拋物線C上,且縱坐標yA=1,所以A(1,1).
設過點Q(3,-1)的直線方程為x-3=m(y+1),即x=my+m+3.
①
式①代入y2=x,得y2-my-m-3=0.
設M(x1,y1),N(x2,y2),由韋達定理得
y1+y2=m,y1y2=-m-3.
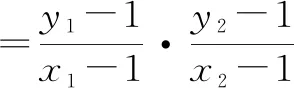
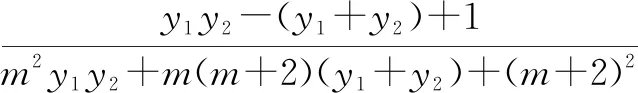
因此,k1k2為定值.
反思:解答時要明確解答的思路,這點并不困難,難點在于聯立方程后結合條件化簡運算.在解題時,不僅要明確題目中的已知數據和要求,還要掌握聯立方程后結合韋達定理進行化簡運算,提高計算能力,掌握計算技巧.
2.2 題型二:面積定值問題
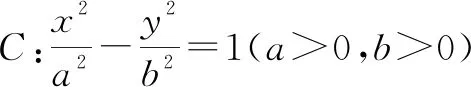
(1)求雙曲線C的方程;
(2)直線l與x軸正半軸相交于一點D,與雙曲線C右支相切(切點不為右頂點),且l分別交雙曲線C的兩條漸近線于M,N兩點,證明:△OMN的面積為定值,并求出該定值.
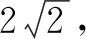
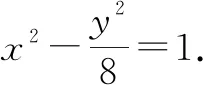
(2)因為直線l與雙曲線C右支相切(切點不為右頂點),所以直線l的斜率存在且不為0.
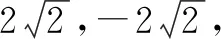
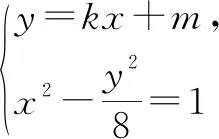
(8-k2)x2-2kmx-m2-8=0.
由直線與雙曲線右支相切得,Δ=4k2m2-4(8-k2)(-m2-8)=0,即8-k2=-m2.

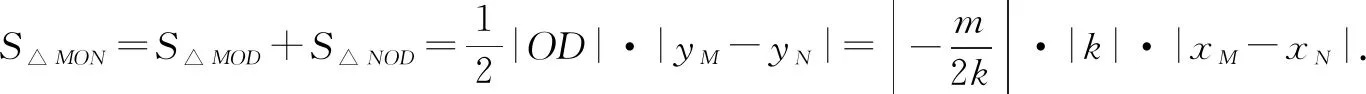

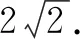
反思:本題考查了雙曲線方程的求解以及直線和雙曲線(或其漸近線)相交時產生的相關面積定值問題.解答時要注意結合圖形的幾何特征合理使用公式.本題需要選擇表示三角形面積的最佳路徑,從而將面積轉化為坐標關系繼而解答,化簡整理時,運算比較繁雜,要十分細心.
2.3 題型三:相關比值定值問題
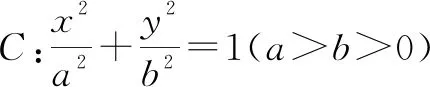
(1)求橢圓C的方程;
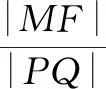
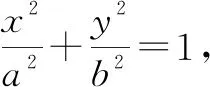
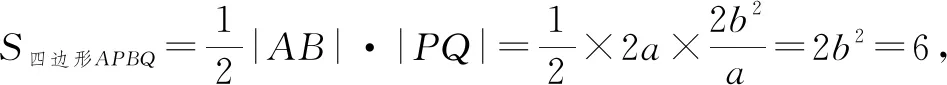
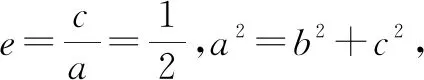
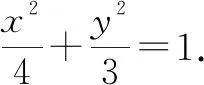
(2)證明:由題意可知,F(1,0),直線l的方程為y=k(x-1).
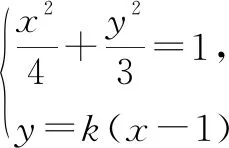
(4k2+3)x2-8k2x+4k2-12=0.
設P(x1,y1),Q(x2,y2),則
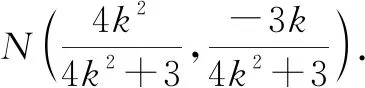
于是直線MN的方程為

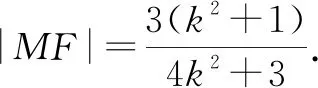

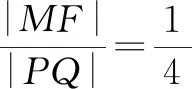
反思:解題過程中要明確解題方法和其中包含的數學思想.
認真審題,分析解題用到的數學思想方法,學會借助韋達定理來表示每一條線段長.當解題思路明晰時,會發現線段長都用核心變量表示出來后就能求出定值.分析時要尋找題目中已經給出來的已知信息,判斷不同數據之間的邏輯關系,在推理中把握聯系,形成客觀性認識,明確思路,快速解題.
3 總結
以上幾種思維策略是高中數學中常用方法,對于較為復雜的問題,可先采用特殊位置(如直線斜率不存在或為0)或者對稱關系求出定值,進而給后面一般情形指明方向;運算中盡量利用變量之間關系(如點的坐標符合曲線方程等)做到整體代入,設而不求,簡化運算.要想在高考中運用自如,需要在平常的解題過程中多加實踐,不斷理清思路,積累經驗,提升邏輯思維能力和運算能力,最終達到對此類題型熟能生巧、胸有成竹.

