知識巧交匯 數列妙應用
?安徽省阜陽市紅旗中學 王茂快
1 引言
在“知識網絡交匯點處設計試題”是高考數學大綱的明確要求與高考數學命題的指導思想之一,作為高中數學的主干知識之一的數列,更是多知識交匯與綜合的重要場所,是創新應用與創新意識的更深層次體現,在高考中的地位將越來越重要,是每年高考數學中的熱點與亮點之一.數列的交匯綜合問題,以數列的相關知識為背景或串聯點,把相關的數學知識加以合理創新與交匯,類型多樣,變化多端,倍受關注.
2 數列與新信息的交匯綜合
含“新信息”情境背景的數列交匯綜合問題,經常以圖表遷移、新運算、新概念、新情境等形式出現.此類問題與新信息相關,變化形式多樣,要運用的相關知識隱藏比較深,破解的關鍵是找到解題的方向,借助數列的相關知識來分析與處理.
例1如圖1,是某省從1月21日至2月24日的新冠肺炎每日新增確診病例變化曲線圖.
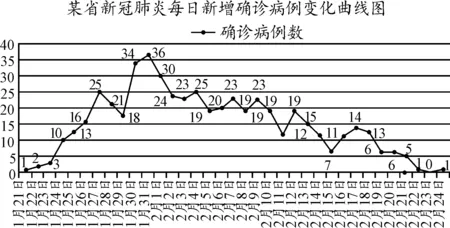
圖1
若該省從1月21日至2月24日的新冠肺炎每日新增確診病例數按日期順序排列構成數列{an},{an}的前n項和為Sn,則下列說法中正確的是( ).
A.數列{an}是遞增數列
B.數列{Sn}是遞增數列
C.數列{an}的最大項是a11
D.數列{Sn}的最大項是S11
解析:因為1月28日的新增確診病例數小于1月27日的新增確診病例數,即a7>a8,所以{an}不是遞增數列,所以選項A錯誤;
因為2月23日新增確診病例數為0,所以S33=S34,所以數列{Sn}不是遞增數列,所以選項B錯誤;
因為1月31日新增確診病例數最多,從1月21日算起,1月31日是第11天,所以數列{an}的最大項是a11,所以選項C正確;
數列{Sn}的最大項是S35,所以選項D錯誤.
故選擇答案:C.
點評:以新情境為問題背景,結合數列的變化曲線圖,利用圖表遷移,數形結合,根據具體的數據建立相應的數列,并結合通項、求和、數列性質等來分析相應的說法的正確性問題.
3 數列與函數的交匯綜合
數列與函數的交匯綜合問題主要包括:(1)借助函數條件來解決數列問題,一般利用函數的圖象與性質來研究數列問題;(2)借助數列條件來解決函數問題,一般利用數列的取值范圍、公式、求和方法,結合式子進行化簡變形來研究函數問題.
例2(多選題)定義在(-∞,0)∪(0,+∞)上的函數f(x),如果對任意給定的等比數列{an},{f(an)}仍是等比數列,那么稱函數f(x)為“保等比數列函數”.現有定義在(-∞,0)∪(0,+∞)上的如下函數,其中是“保等比數列函數”的為( ).
A.f(x)=x3B.f(x)=ex
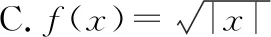
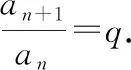
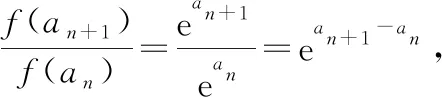
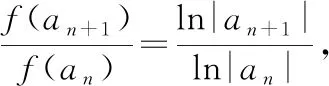
故選擇答案:AC.
點評:以創新函數定義為問題背景,結合數列與函數的交匯綜合來設置問題,借助函數的解析式,通過等比數列的定義與性質,對比創新定義逐一剖析,進而判定是否滿足對應的創新定義問題.
4 數列與不等式的交匯綜合
數列與不等式的交匯綜合問題主要包括:(1)研究數列中項或前n項和的最值,一般利用數列的單調性來解決;(2)研究數列與不等式的交匯融合,一般通過分解、轉化為數列與不等式單獨的問題,各自利用相關知識點來解決.
例3已知Sn是等差數列{an}的前n項和,設bn=anan+1an+2,若S7 A.6 B.7 C.8 D.9 解析:由S7 設等差數列{an}的公差為d. 由于a8+a9+a10>0,即3(a1+8d)>0,可得a9>0.又a9+a10<0,則知a10<0,所以d<0. 所以等差數列{an}是遞減數列,且a7>0,a8>0,a9>0,a10<0. 所以b1>0,b2>0,……,b7>0,b8<0,b9>0,b10<0,b11<0,…… 由于b9+b8=a9a10(a11+a8),a11+a8=a9+a10<0,a10<0,a9>0,所以b9+b8>0,即當Tn取得最大值時,n=9. 故選擇答案:D. 點評:以等差數列的前n項和對應的不等關系式為問題背景,通過求和公式的轉化建立相應的不等式組,通過不等關系式的變形與轉化,確定數列的單調性與最值,進而確定數列的項數問題. 數列與解析幾何的交匯綜合,經常借助解析幾何曲線上點的坐標關系等來探究數列的遞推關系式問題.破解的步驟是:①分析曲線上點的坐標滿足的條件;②探究數列的遞推關系式,并進行檢驗. 圖2 解析:當r1=1時,圓C1:x2+(y-a1)2=1. 將圓C1的方程與y=x2聯立,消去x,得y2-(2a1-1)y+a12-1=0. 由圖可知當n≥2時,an=an-1+rn-1+rn. ① 將x2+(y-an)2=rn2與y=x2聯立,消去x,得 y2-(2an-1)y+an2-rn2=0. ② 點評:以平面解析幾何為問題背景,通過曲線與圓的相切,結合函數與方程思維的應用,代入消參,建立對應的方程,并利用判別式的建立與轉化來確定數列的遞推關系式,進而結合數列的相關知識來分析與處理. 數列與平面向量的交匯綜合問題往往是把數列的項或前n項和滲透在平面向量的線性運算或坐標運算中,利用向量滿足的條件轉化得到數列的遞推關系式,進一步解決數列的相關問題. A.31 B.33 C.63 D.65 解析:如圖3所示,連接BD,設AC與BD交于點O,過點B作BE⊥AC于點E,過點D作DF⊥AC于點F.因為△ACD的面積是△ABC的面積的2倍,所以DF=2BE. 圖3 所以 an+1-3=2(an-2), 即 an+1-1=2(an-1). 因此,數列{an-1}是首項為a1-1=2,公比為2的等比數列,an-1=2×2n-1=2n,則an=2n+1,從而a5=25+1=33. 故選擇答案:B. 點評:以平面幾何圖形為問題背景,結合平面幾何的相關知識、平面向量的線性運算等加以分解與展開,巧妙轉化并確定平面向量的相關參數,建立數列的遞推關系式,為數列的進一步分析與求解提供條件. 數列與其他知識的交匯綜合問題,一直都是歷年高考數學中的重點所在與熟悉面孔,巧妙通過數與形的結合,溝通不同數學知識之間的關聯,增加數學之間的交匯與綜合,提升問題的趣味性與拓展性,增強創新意識與創新應用,提升數學能力,提高數學品質,培養數學核心素養.5 數列與解析幾何的交匯綜合
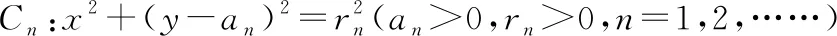
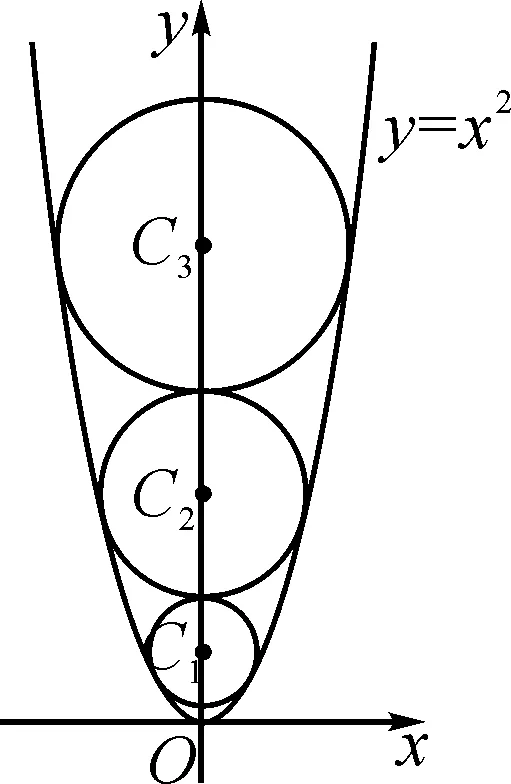
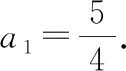
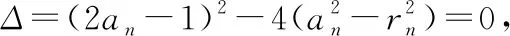
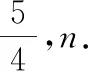
6 數列與平面向量的交匯綜合
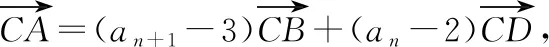
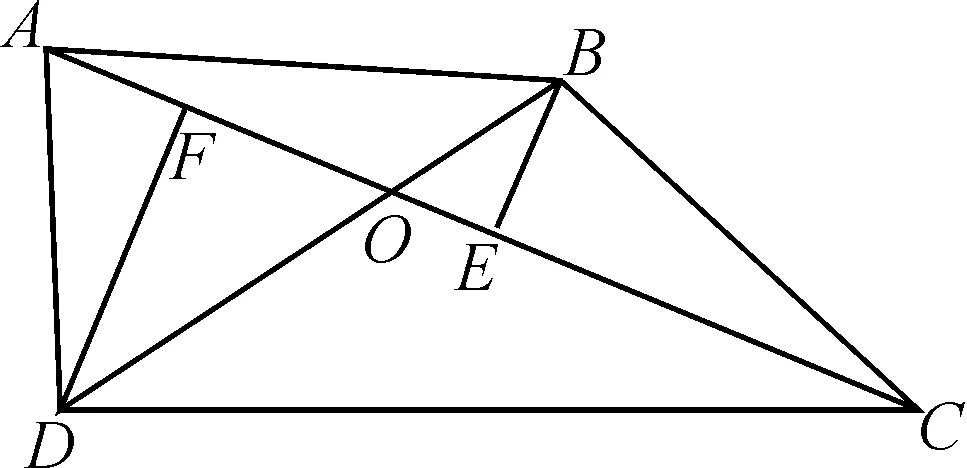

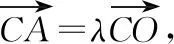
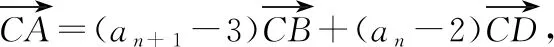
7 結束語

