水驅油田動態相對滲透率計算方法適用性研究

劉新光，李南，張金慶，張利軍，鄭偉

1.中國海洋石油國際有限公司海外技術支持中心，北京102200 2.中海油研究總院有限公司勘探開發研究院，北京102200

油水相對滲透率曲線(以下簡稱相滲曲線)是油田開發最為關鍵的基礎參數，是水驅油田含水上升規律、產量遞減規律和采收率的決定因素[1,2]。實際油田開發過程中，由于巖心取樣數量和試驗費用的制約，往往僅對部分層位、井區開展相滲曲線試驗。隨開發時間的增長，相滲曲線會發生變化[3,4]，可能與早期試驗測試的相對滲透率相差較大。動態相滲曲線是通過生產井的實際油水產量反求得到的油水相滲曲線，既反映了實際巖石和流體特性，也包括了真實油藏的非均質性[5]。在方法合理的情況下，動態相滲的代表性較強，對油田開發后續預測更具指導作用。由于反函數的求解具備一定的多解性，一些文獻中使用多次迭代[6,7]或者遺傳算法[8]來尋找最優解的方式確定相滲的關鍵參數，但需要編程計算，方法求解難度較大，多次迭代也增加了不可控性，很多算例難以得到合理的結果。文獻[9.10]采用相對滲透率的指數表達式，直接利用含水率與水油比的關系來計算相滲曲線，簡化了曲線求解的過程。文獻[11]采用相滲曲線指數表達式推導了張型近似理論水驅曲線，通過生產數據擬合水驅曲線求解待定參數來確定相滲關鍵參數，得到動態相滲。

在實際應用中發現，不同方法計算結果存在較大的差異，需要科學對比確定合理的計算方法，明確方法的適用油藏類型，以便對后續應用進行指導。通過數值模擬計算的油水產量數據，使用不同方法計算動態相滲曲線，對比動態相滲與數值模擬輸入相滲及動態相滲計算的無量綱采油采液指數和模型中輸出的產量、壓差數據計算的無量綱采油采液指數[12]來綜合判斷動態相滲計算方法的合理性，并驗證方法對油藏類型的適用性。

1 數值模型的建立

采用Eclipse軟件建立數值模擬模型。

注水油藏直井開發模型(見圖1(a))：網格數為21×21×20，網格步長為20m×20m×1m，地層傾角為0°，無天然水體，孔隙度30%，滲透率1500mD，原油黏度μo=50mPa·s，地層水黏度μw=0.5mPa·s，模型輸入相滲為渤海遼東灣地區某油田實驗室測定的相滲曲線(如圖2所示)。該類油藏常采用直井規則井網開發，取五點注水井網的1/4模型(1注1采)，注采井間距594m，模型厚度20m，生產控制條件為定油限液限流壓生產，生產井日產油量目標300m3，最大日產液量1000m3，最低井底流壓4MPa；注水井最高注入量1000m3/d，注采平衡，最高井底流壓14MPa，生產時間20年。

邊水油藏水平井開發模型(見圖1(b))：網格數15×30×10，網格步長20m×20m×1m，地層傾角3°，水體倍數20倍。該類油藏適合采用水平井天然能量開發，以促進水線均勻推進，設計水平井長度280m，水平井距內含油邊界400m，其他條件同注水油藏直井開發模型。

底水油藏水平井開發模型(見圖1(c))：網格數21×21×20，網格步長20m×20m×1m，地層傾角0°，水體倍數20倍，該類油藏適合采用水平井天然能量開發，盡量緩解底水錐進速度。設計水平井長度280m，避射高度20m，其他條件同注水油藏直井開發模型。

圖1 不同油藏類型開發模型示意圖

2 動態相滲求解方法的驗證

采用注水油藏直井開發模型計算結果，對應用較廣的水油比法和張型近似理論水驅曲線法進行驗證。

2.1 水油比法合理性驗證

相滲的指數式表達式：

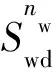
(1)

Kro=Kro(Swi)(1-Swd)no

(2)

根據平面徑向流公式：

(3)

(4)

式中：Kro、Krw分別為油相相對滲透率、水相相對滲透率，1；Krw(Sor)為殘余油飽和度下的水相相對滲透率，1；Kro(Swi)為束縛水飽和度下的油相相對滲透率，1；Swd為歸一化的含水飽和度，1；no、nw分別為相滲的指數式表達式中的油相指數、水相指數，1；Qo、Qw分別為產油量、產水量，m3/d；K為有效滲透率，mD；h為油層厚度，m；Δp為生產壓差，MPa；μo、μw分別為地層原油黏度、地層水黏度，mPa·s；Bo、Bw分別為油相體積系數、水相體積系數，m3/m3；re、rw分別為泄油半徑、井筒半徑，m。

假設油水相生產壓差相等、供液半徑相同，并將式(1)、式(2)代入式(3)、式(4)，可得到水油產量比為：

(5)

根據定義，Swd可表示為可動油儲量采出程度Rf，即:

(6)

對式(5)兩邊取對數并將式(6)代入可得到二元一次方程形式：

(7)

其中:

(8)

式中：Np為某一時刻累計產油量，m3；NR為含水率到達100%時的累計采油量，m3；M為水油流度比與油水體積系數比的乘積，1。

使用甲型水驅曲線擬合數值模擬結果中產油、產液量數據，得到NR=30.4×104m3，之后擬合式(7)，多元回歸得到M=71.3，nw=2.43，no=1.34。根據式(8)得到Krw(Sor)=0.713，之后根據式(1)繪制出相滲曲線，如圖2所示。對比可見，水油比法計算的動態相滲曲線明顯高于數模相滲，兩者存在著較大差異。

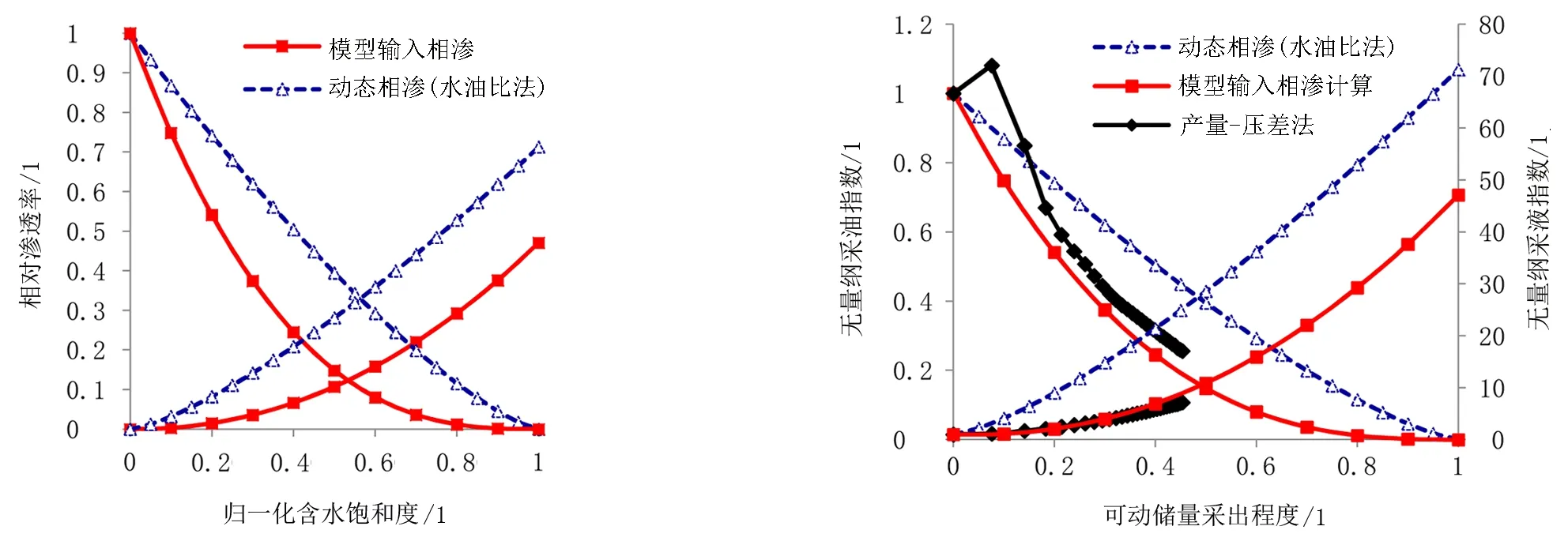
圖2 水油比法動態相滲與模型輸入相滲比較 圖3 水油比法動態相滲與模型輸入相滲和產量-壓差計算無量綱采油采液指數比較

無量綱采油、采液指數為某一時刻下的采油、采液指數與初始狀況下的采油、采液指數的比值，其定義為式(9)。圖3中黑色實線為模型中產油、產液和生產壓差數據計算得到的無量綱采油、采液指數曲線。

(9)

根據文獻[11]，無量綱采油、采液指數可使用相滲參數表示為式(10)，可分別繪制出水油比法動態相滲和模型輸入相滲對應的無量綱采油采液指數曲線，如圖3中的藍色虛線和紅色實線。

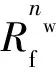
(10)

式中：Jdo、Jdl分別為無量綱采油指數、無量綱采液指數，1；Jo、Jl分別為某一時刻下的采油指數、采液指數，m3/(MPa·d)；Joi、Jli分別為無水采油期的采油指數、采液指數，m3/(MPa·d)；Rf為可采儲量采出程度，1。

模型中每個網格均按照輸入相滲進行計算，若動態相滲計算方法正確，回歸得到的動態相滲應與模型的輸入相滲接近；使用動態相滲計算的無量綱采油采液指數應該與模型給出的壓差-流量計算的無量綱采油采液指數接近，這種情況下采用動態相滲才具有其對實際生產的預測和指導意義。通過對比可見，由水油比法繪制的無量綱采油采液指數高于數模輸入相滲和根據產量-壓差計算得到的無量綱采油采液指數。這說明水油比法計算的動態相滲誤差過大，不能代表實際相滲，由此計算的無量綱采油采液指數也不能用于現場預測。水油比法假設油相、水相的壓差和泄油半徑相同，其過程類似于穩態法油水相滲試驗過程[13，14]，即在油藏或巖心的一端注入一定比例的油和水，在另一端產出相同比例的油和水。而實際油田的開發類似于非穩態法相滲試驗過程，即在油藏或巖心的一端注入水，在另一端產出油和水，生產過程中油相和水相的壓差、飽和度都在不斷變化，不能近似為相等，式(5)不能成立。

2.2 張型近似理論水驅曲線法合理性驗證

文獻[11]根據相滲的指數式表達式推導出了近似理論水驅曲線，建立了水驅曲線的回歸參數與相滲關鍵參數之間的關系式，具體過程如下。

根據相滲的指數表達式及分流量方程，在忽略重力和毛細管壓力時，可得到:

(11)

由于:

(12)

則:

(13)

式(13)無法積分，但在被積函數的分子上加上一項高階小項后可近似得到：

(14)

式(14)可積分得到原函數，即:

(15)

整理可得到張型近似理論水驅曲線：

(16)

其中，p、q、a的表達式如下：

(17)

式中：Wp為累計產水量,m3；p、q、a為張型近似理論水驅曲線法待定系數，1。

因此，通過生產參數回歸張型近似理論水驅曲線，得到待定系數p、q、a后，可以計算相滲的關鍵參數nw、no、M及Krw(Sor)，從而得到動態相滲。由于該水驅曲線存在p、q、a、NR四個未知數，很難同時求解，具體操作過程中，建議首先假設p=2，即張型廣適水驅曲線擬合得到q，再將p在2的基礎上微調以使反算的Wp、fw擬合程度更高(圖4(a))，再獲得p、a(圖4(b)中斜率的負數)、NR(圖4(b)中的截距)3個參數。使用注水油藏模型輸出結果擬合式(14)，如圖4所示，求得的a=2.5342，q=0.75，NR=29.824×104m3，M=26.92，nw=1.65，no=2.34。

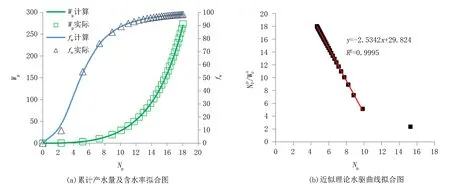
圖4 張型近似理論水驅曲線擬合曲線

根據相滲參數，繪制動態相滲與模型輸入相滲對比圖(見圖5)，可見張型近似理論水驅曲線法計算的動態相滲與模型輸入相滲之間有一定的差異，但較水油比法差異明顯減小。繪制不同方法的無量綱采油采液指數曲線圖(見圖6)，可見由張型近似理論水驅曲線法計算的無量綱采油采液指數與根據產量-壓差計算得到的結果幾乎完全重合，其精度高于根據模型輸入相滲計算結果。可見，根據張型近似理論水驅曲線法計算的動態相滲能夠綜合考慮油田生產過程中相滲曲線、壓力變化、平衡控制等一系列因素，雖然與模型輸入相滲略有差異，但更能夠代表油田總體情況，據此做出的預測也更加精確。

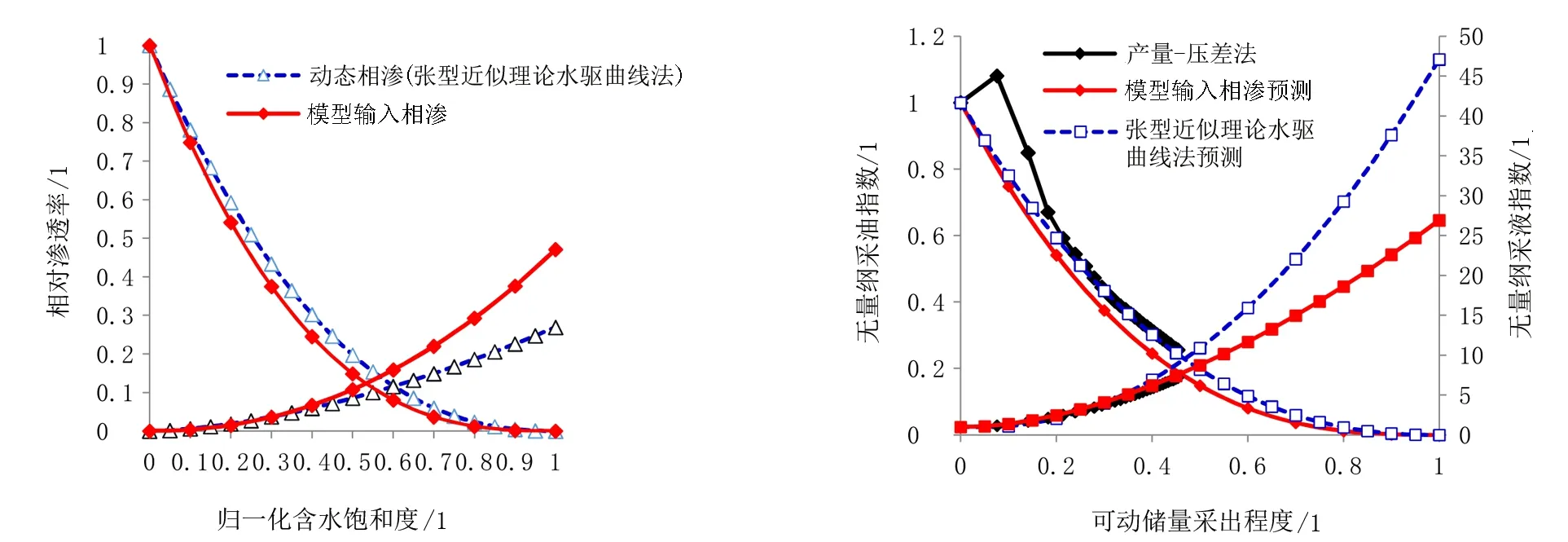
圖5 張型近似理論水驅曲線法動態相滲產量-壓差法計算無量綱采油采液指數比較圖 圖6 張型近似理論水驅曲線法、模型輸入相滲和與模型輸入相滲比較圖

3 不同油藏類型驗證

采用張型近似理論水驅曲線法，進行邊水驅和底水驅油藏動態相滲的計算，并繪制無量綱采油采液指數對比曲線，結果如圖7所示。對比可見，天然水驅邊水油藏的動態相滲與模型輸入相滲基本相同，根據相滲參數計算的無量綱采油采液指數曲線幾乎完全重合，但兩者與數模模型中根據產量-壓差計算的采油采液指數略有差異；底水驅油藏的動態相滲與輸入相滲差異較大，根據相滲參數計算的無量綱采油采液指數與模型中根據流量-壓差計算的無量綱采油采液指數的差異也較大。由此可見，張型近似理論水驅曲線法計算的動態相滲對于傾角較小的注水開發油藏和天然邊水驅動油藏的適應性較好，能夠進行后續產量、提液時機等因素的預測[15]，但對于底水驅動油藏，由于公式(9)推導過程忽略了重力的影響，其誤差較大。

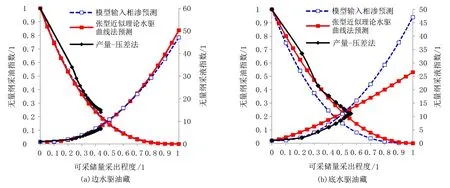
圖7 天然水驅油藏水平井開發無量綱采油采液指數比較圖

4 應用實例

SZ油田為典型海上注水開發油藏，以該油田處于油藏內部且開發歷史較長、生產較為連續的D02井為例，其生產曲線如圖8所示。采用張型近似理論水驅曲線法計算得到no=2.3，nw=1.7，M=31.5。該油田同一層位17條相滲曲線歸一化后得到的no=2.19，nw=1.81，M=32.3。2種方法得到的相滲曲線對比圖如圖9所示(動態相滲無法計算束縛水飽和度與殘余油飽和度，借用試驗相滲Swi=0.31,Sor=0.25)。可見張型近似理論水驅曲線法計算的動態相滲與試驗相滲曲線一致性高。因此，對于無試驗相滲的已開發油田、區塊或特殊的層位，可使用動態相滲作為參考。

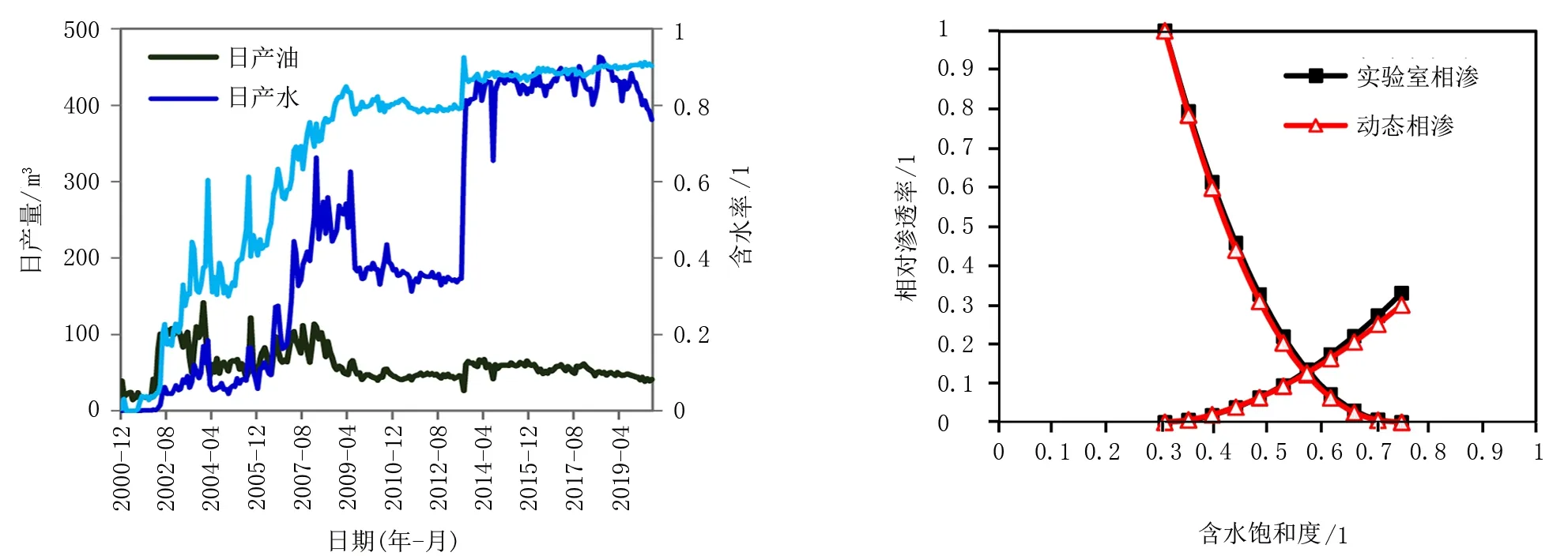
圖8 SZ-D02井生產動態曲線 圖9 實驗室相滲與動態相滲對比圖

5 結論

1)通過數值模擬機理模型中輸入相滲和產量-壓差法計算無量綱采油采液指數的對比表明，張型近似理論水驅曲線法的計算精度遠高于水油比法；水油比法的物理意義基于穩態法相滲試驗測定方法，其基本假設不適用于水驅油田開發過程。

2)地層傾角較小的注水開發油田和邊水驅動油田中，張型近似理論水驅曲線法計算動態相滲預測精度較高，底水驅動油田的預測精度較低。

3)典型案例計算表明，張型近似理論水驅曲線法預測的動態相滲形態與實驗室巖心相滲歸一化結果較為接近，可以作為無實驗相滲的油田、區塊或層位的參考。