基于優化算法的軸流風機數值模擬及實驗研究

高 宇

(1.貴州航天林泉電機有限公司，貴州 貴陽 550081；2.國家精密微特電機工程技術研究中心，貴州 貴陽 550081)

0 引言

風機系統基本工作原理如下：控制器接收上層系統指令并驅動電機帶動葉輪旋轉，葉輪旋轉后產生一定的風壓、風量，為設備散熱提供通風。由于目前軸流風機工作范圍窄、效率低，與工業效率高、能耗低的需求背道而馳。因此，如何利用CFD技術與優化理論相結合，是開發軸流風機產品的關鍵問題之一。

Holland提出的遺傳算法，根據“適者生存”法則，模仿生物進化過程中的遺傳機制。Lee等人[1]將CFD技術與遺傳算法相結合并應用在二維翼型優化設計之中。Hwang等人[2]研究葉輪機幾何參數與效率之間的相關性，數值優化后效率提高25%。

O.Lotf等人[3]應用遺傳算法對二維翼型進行優化，降低總壓損失系數的同時提升了效率。Benini[4]對多種翼型進行設計優化，驗證了遺傳算法應用在翼型優化上的可行性。安志強等人[5]將流場正問題與遺傳算法相結合，建立葉型優化模型，結果顯示全壓和流量分布提高1.1%和6.5%。Lian等人[6-7]利用超立方實驗設計，配合響應面近似模型對三種型式葉輪機械葉片展開了優化設計，結果顯示單級和多級軸流泵的揚程分別提升1.2%和0.5%。

1 數值模擬研究

1.1 湍流模型可靠性驗證

為了確保數值計算結果更加真實可靠，在此之前必須進行湍流模型驗證。但是在高雷諾數下，目前要直接求解全N-S方程異常困難，于是雷諾時均方程法(RANS)常用于求解N-S方程。

RANS用時均值和脈動值之和表示紊流瞬時量，用可以確定的低階量來表示未知的高階量，進而封閉N-S方程組。由雷諾應力不同確定方式，將該方法分為湍流粘性系數法和雷諾應力法，其中湍流粘性系數法廣泛應用于工程之中。因為SSTk-ω湍流模型適用范圍廣、精度高，本文應用SSTk-ω模型作為計算模型。

1.2 計算網格及邊界條件

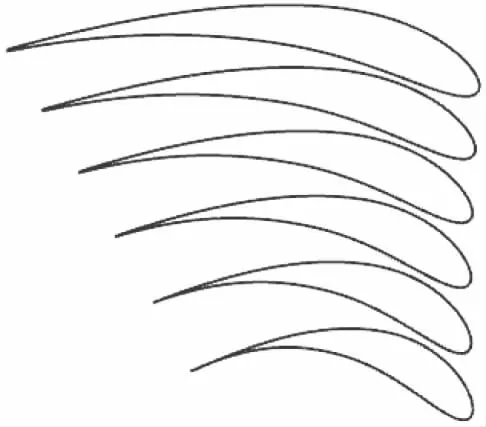
圖1 翼型

翼型如圖1所示，旋轉區域采用六面體全結構化網格，靜止區域采用六面體與四面體混合網格，壁面采用棱柱網格，圖2為動葉和導葉表面網格。利用SSTk-ω湍流模型對風機流場進行數值模擬，研究風機扇葉和涵道流場的相互作用關系，對流項采用二階高階精度迎風格式，進口為質量流量進口，出口為大氣壓力。

圖2 葉片表面結構化網格

1.3 扇葉、涵道主要關鍵參數敏感度分析

通過最優拉丁超立方方法取樣本點均勻分布在設計空間，通過EE方法對樣本點進行分析得到各設計變量對性能及效率的影響大小如圖3和圖4，由圖3看出，葉片中部的弦長和安放角對靜壓的影響最大，高達24.19%和20.16%，靜壓對掠角和涵道收縮角敏感度最低；由圖4看出，葉片中部的弦長和掠角對效率的影響最大，可達到17.8%和18.81%，效率對彎角和葉片中部的安放角敏感度最低。在優化過程中，應該抓住對靜壓和效率影響較大的優化變量，忽略對靜壓和效率影響較小的參數以減少優化變量，提高優化效率，從而節約計算資源和時間。

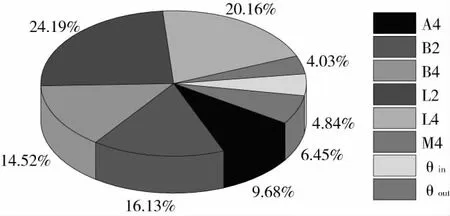
圖3 優化變量對靜壓的影響比例

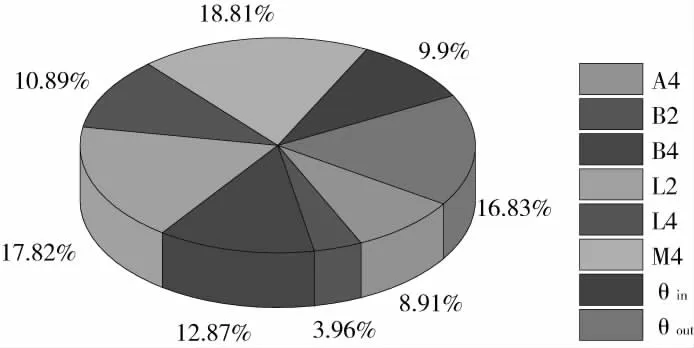
圖4 優化變量對效率的影響比例

由上可知，應該把弦長、安放角、掠角三個參數作為優化變量，在提高優化效率的同時，獲得較好的優化效果。

1.4 優化后扇葉-涵道流場作用關系

1)關鍵技術分析

風壓和風量、噪聲、效率等關鍵氣動性能技術指標受到風機轉速、葉片幾何參數、扇葉和涵道一體化耦合作用等多因素影響，設計要求轉速為15000 rpm條件下，風壓風量要大于400 Pa、70 CFM，同時噪聲在(67 Pa，13.6 CFM)、(18.3 CFM，115 Pa)工況下分別小于47.5 dB、55 dB，技術指標要求極高，采用傳統的設計方法無法滿足設計要求，擬采用優化設計。

2)流體優化方案

①風機氣動優化策略

由于風機整機尺寸受到軸向和徑向尺寸的限制；加工工藝對扇葉形狀的約束；無普遍適用的彎掠角設計方法等因素制約，無法采用傳統的二元設計方法，因此采用優化設計的方法，同時優化扇葉、涵道和導葉，優化變量太多，時間成本和優化矩陣樣本過大，時間成本不經濟，所以采用逐一優化的策略。

②扇葉優化設計

在NACA翼型數據庫中搜索葉片基本形狀，首先將涵道定義為直管，進出口無收縮、擴張段，采用代理模型法將安放角、弦長、掠角為優化變量，靜壓為目標函數；其次在前兩個最高點進行局部優化，將不同圓柱面上的翼型安放角、弦長、彎角作為優化變量，利用代理模型的優化方法進行優化。優化后的空間示意和葉片如圖5所示。扇葉優化設計基于代理模型的全局優化方法，采用最優拉丁超立方正交實驗設計，代理模型采用Kriging方法，利用遺傳算法進行優化。

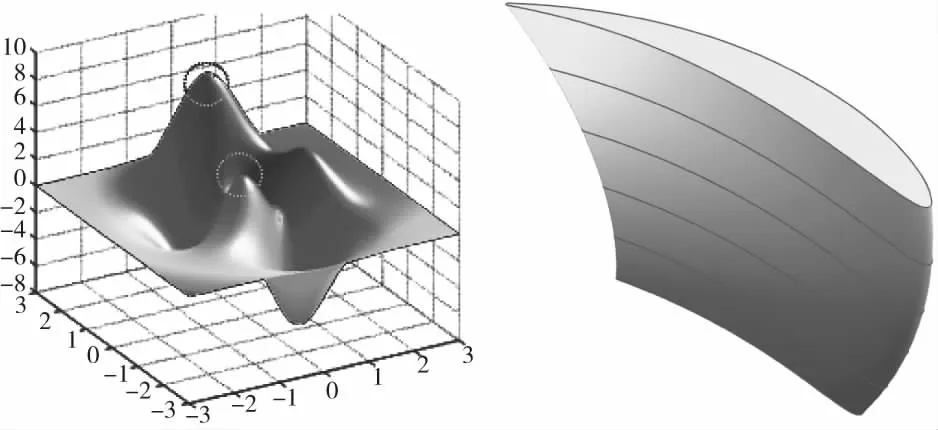
圖5 局部優化空間示意圖和優化后的葉片

③涵道、導葉優化設計

利用代理模型法將涵道的進口收縮角、出口擴散角、導葉安放角和彎角為優化變量，靜壓為目標函數進行優化，將優化后的結果與扇葉耦合，進行扇葉-涵道耦合一體化設計，優化后的涵道和導葉如圖6所示，最終將設計出來的風機進行CFD數值計算并進行實驗驗證。

④CFD數值計算

圖6 涵道、導葉優化變量

利用CFX軟件進行數值模擬，采用SSTk-ω湍流模型，保證葉片、導葉第1層網格高度為0.002 mm，葉片吸力面、壓力面最高y+<1，葉頂最高y+<10，邊界條件為總壓進口，質量流量出口，對流項為高階離散格式，計算模型及網格劃分如圖7、圖8所示。

圖7 數值計算模型

圖8 葉片表面網格和y+分布

風機在設計點下不同葉高截面的壓力云圖如圖9所示。在葉片根部附近(即10%葉高截面)吸力面尾緣未出現大面積的低壓區，未出現附面層分離，壓力沿著吸力面前緣到尾緣逐漸增加，壓力面與吸力面壓差增大，從而形成較大環量。沿著葉高方向，逐漸減小翼型安放角與來流沖角之間的角度，降低葉片分離現象達到改善流動的效果。根據以上分析，通道內壓力分布合理，從而有效降低了翼型的流動分離，使效率得到提高。

風機全三維流線圖如圖10所示，由圖10可知風機內流線分布合理，沒有特別大的漩渦區，可以大大降低損失進而提高風機效率。風機在工作點下沿葉高方向的速度流線圖和湍動能云圖如圖11和圖12所示。風機在壓力面中部弦長出現附面層分離，但是在葉片尾緣處流體又重新附著在葉片表面，吸力面的流動分離現象不明顯。

圖9 不同葉高截面壓力云圖

圖10 優化后風機三維流線圖

圖11 不同葉高截面速度流線圖

圖12 不同葉高截面湍動能云圖

葉片靜壓沿著葉高方向變化如圖13所示，由圖13可知，沿著高度方向葉片表面靜壓逐漸增大，吸力面的靜壓在不同葉高方向比較接近，葉片從前緣到尾緣壓力梯度不斷降低，在葉片前緣附近沿著葉片高度方向壓力梯度逐漸增加，靜壓在葉片吸力面前緣變化更為劇烈，在10%和50%葉高范圍內葉片通道逆壓力梯度大，附面層很容易分離，葉片90%葉高周圍由于葉片厚度較薄，因此分離區范圍和靜壓變化更大。

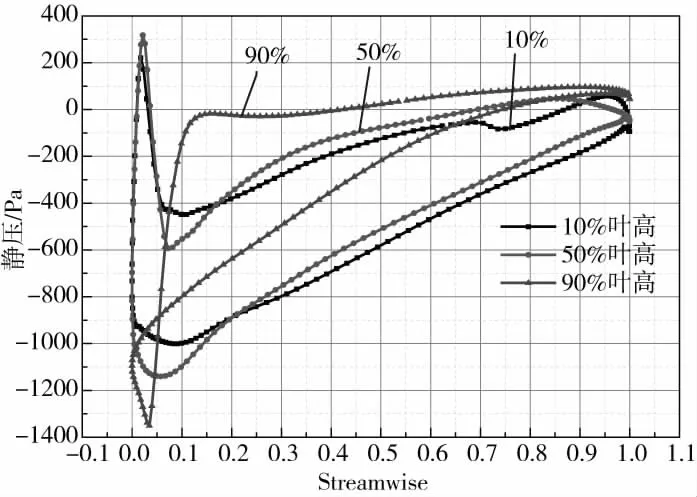
圖13 不同葉高葉片表面靜壓分布

流道總壓沿著軸向變化如圖14所示，總壓表示單位流體所能攜帶能量的多少，可用其表征流體在運動過程中流體的流動損失。如圖14所示，在進口區域總壓基本維持不變，在葉輪區域由于葉輪的旋轉做功導致總壓快速增大，在導葉區域稍微有所下降。大約在葉片前1/5部位總壓上升梯度明顯高于葉片后部；總壓在導葉區域下降較小，下降大小約為50 Pa，總的來說流體流經導葉之后總壓變化不明顯。

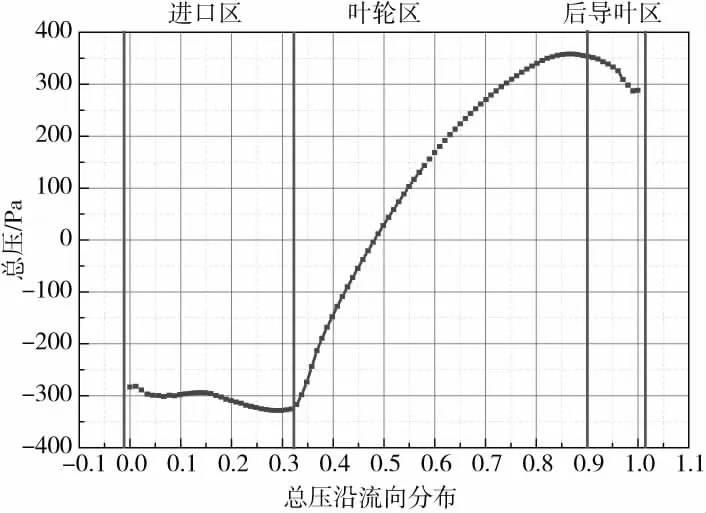
圖14 總壓沿流向分布

圖15為通過數值模擬得到的風機的性能曲線。由圖15可見：所設計的風機性能達到了預定的設計參數，效率最優位置在設計點附近，效率最高點達到81%，隨著流量的增加，效率先增加達到最大然后降低；風機的性能應能夠滿足風機的使用要求(70 CFM下406 Pa)，小流量點設計要求中所給的參數遠低于所設計風機的性能。

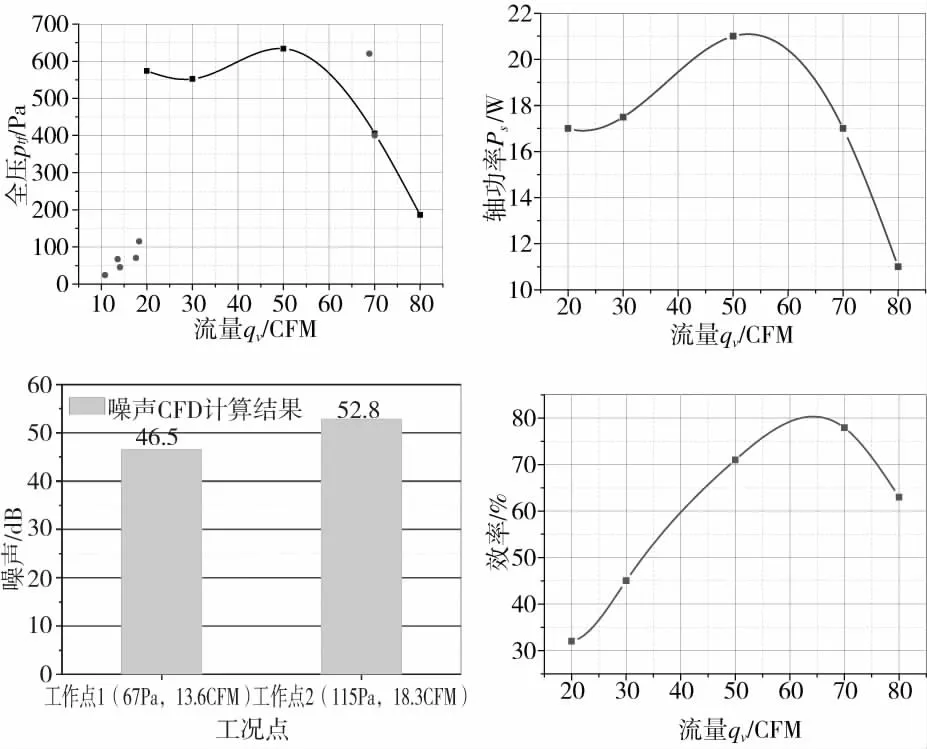
圖15 風機性能曲線

2 實驗研究

2.1 實驗系統介紹

圖16是風機動葉面和靜葉面的三維實物圖，風機一共由葉框、葉輪、控制器、電機幾個部分組成，控制器接收上層系統指定并驅動電機帶動葉輪旋轉，葉輪旋轉后產生一定的風壓、風量，為設備散熱提供通風。圖17為實驗系統圖，用于測量風機的風壓、風量以及噪聲。

圖16 風機實物圖

圖17 風壓、風量和噪聲實驗系統圖

2.2 實驗結果分析

由圖18可知，工作點附近實驗結果和數值計算很接近，但是在其他流量點兩者相差較大，因此風機盡量工作在工作點附近，隨著流量增加靜壓不斷降低，當流量達到70 CFM時，靜壓超過了400 Pa，而數值模擬結果為406 Pa，實驗和數值模擬結果相差1.5%(部分由幾何模型差異引起)，驗證了數值計算的可靠性，最大風量可以達到123 CFM，最大靜壓達到930 Pa。

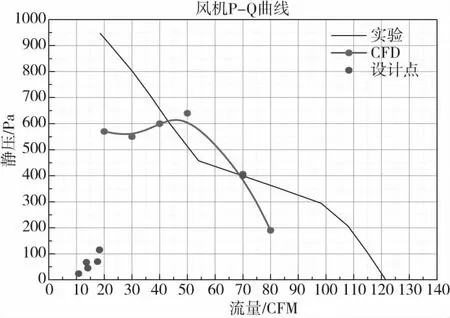
圖18 風機P-Q曲線

圖19為風機噪音在不同工況下實驗和數值模擬比較，由圖19可知，風機在(13.6 CFM，67 Pa)、(18.3 CFM，115 Pa)兩個工況點下，實驗的噪聲結果偏高，可能是由于環境噪聲和機械噪聲引起。

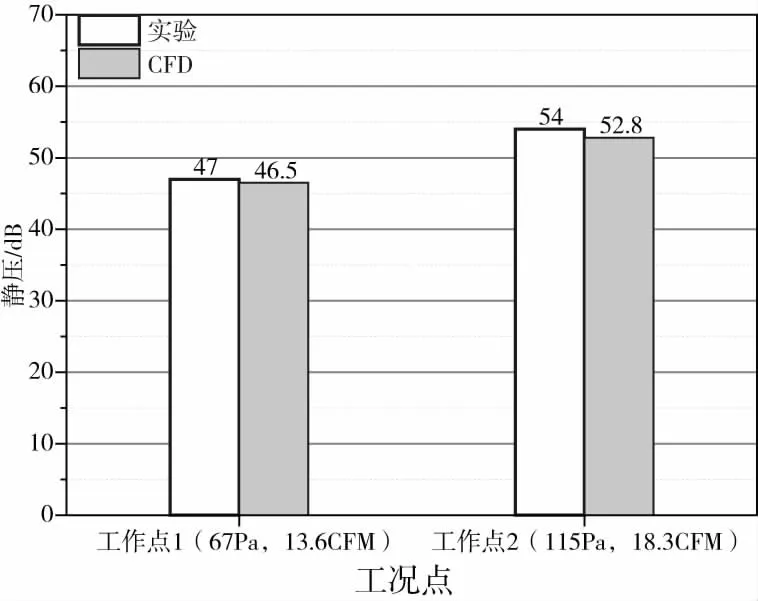
圖19 噪聲在不同工況下實驗和CFD計算結果對比

表1為風機性能參數實驗結果與數值模擬結果比較。由表1可知，靜壓和效率與數值計算結果相比偏低，噪聲偏高，但是最大誤差都在正負5%以內，證明了所采用的優化策略的可行性和數值模擬方法的準確性。

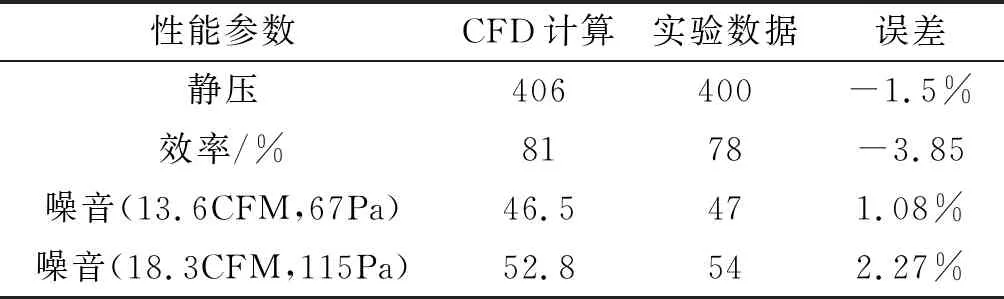
表1 實驗數據與CFD計算結果比較

3 總結

本文討論了軸流風機流動特性和風壓、風量、效率和噪音與風機幾何參數之間的關系，通過數值模擬和實驗研究，得到如下結論：

1)通過DOE實驗設計，利用拉丁超立方形成優化變量矩陣，結合CFD計算結果建立相似模型，采用遺傳算法尋優能夠大大提高風機的氣動性能；

2)通過實驗研究，驗證了數值模擬方法的準確性，優化后風機最大流量可達123 CFM，最大靜壓達到930 Pa；

3)優化后風機的最大效率得到改善，最大效率為81%，氣動噪音變低，數值計算和實驗結果最大誤差不超過5%，驗證了數值模擬結果的準確性。