基于3DCS的換電站充電倉尺寸分析應用

付紅圣，隆 橋，羅鈞鼎

(上海蔚來汽車有限公司，上海 201800)

0 引言

隨著電動汽車產量和保有量不斷增加，電動汽車補能成了業內的難題。電動汽車的能源供給形式主要包含2類：充電模式和換電模式。相對于傳統的充電模式，換電模式可以使電動汽車不必搭載太多電量的電池，甚至允許用戶只購買車殼，大大降低了用戶的購買成本。此外換電模式還具有更高效、更快捷等優點[1]。截止2020年11月，全國已建成535座換電站，并預計在2025年全國建成超過9000座換電站[2]。充電倉作為換電站的核心組件，是電池充電、存貯、轉運的重要場所。廠家和消費者對充電倉的關注點主要集中在安全、換電時間、容量(同時充電數)、自動化無人值守等方面。充電倉作為一個高度機械化的部件，當出現尺寸類問題，例如電池尺寸超標導致卡滯，會造成顧客等待時間長甚至換電站停用等風險，對安全、自動化無人值守也帶來了非常大的不穩定因素。因此在換電站設計前期，結合空間布置，存取方式，零部件定位策略，電池的互換性、功能需求等方面，進行系統化的尺寸分析和設計，可提前有效規避和降低換電站尺寸問題的發生，提高換電站的經濟價值和服務質量。

1 充電倉裝配性校核意義

傳統的汽車功能件裝配性校核覆蓋產品設計、工藝設計、零部件制造、質量保證和裝配的全過程，根據性能目標和計算結果延伸并影響到零件的模具設計、夾具設計、檢具設計和測量設計等[3]。換電站充電倉的裝配性分析與之大體相同，但也有部分差異：一般汽車零部件彼此之間的配合為一次，而換電站卻要求電池適配不同的換電站，換電站也要能兼容所有適用的電池，即對零部件互換性有更高的要求。充電倉的關鍵尺寸功能主要有兩點：第一是不同的電池是否都能進入不同的充電倉位，不發生卡滯，滿足互換性要求；第二是電池進入充電倉位后，既定的定位策略和容差結構能否讓冷卻液插頭和電插頭(下文簡稱水電插頭)準確插入電池上對應的插座上。本文主要基于這兩點進行尺寸分析應用介紹。

2 換電站充電倉定位策略

尺寸分析的基礎是先確定分析對象的定位策略。換電站充電倉定位策略基于多個維度進行制定，如換電站整體空間、電池倉容量、零部件的精度水平、容差機構及容差大小、可接受失效率、成本等。尤其是空間、電池容量大小對定位策略的制動起了決定性的作用。現基于某換電站的相關輸入：

1.空間：底面積為兩個標準車位，高度與標準集裝箱等高；

2.電池容量：1X塊；

3.容差結構的容差量：+/-X mm；

4.可接受失效率：0.0X%；

5.成本：XX萬；

……

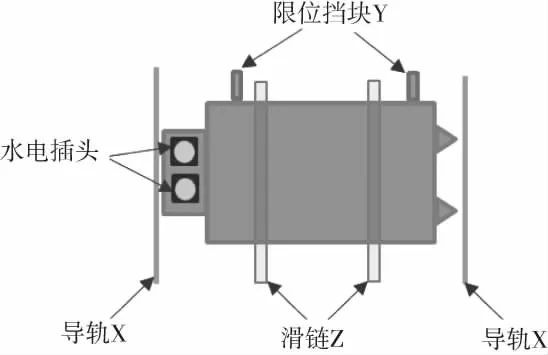
圖1 充電倉電池定位策略

上述輸入制定后，最考驗的是空間布置，需要在較小的空間下布置1X塊電池，對空間結構的要求非常苛刻，經過綜合評估和判斷，確定了導軌定位的策略，如圖1所示：電池通過電池下方的兩條電動滑鏈(定位Z向，限制3個自由度)傳動進入充電倉位(兩個的導軌共同定位X向，限制2個自由度)，內側的兩個限位塊進行橫向限位(定位Y向，限制1個自由度)。之后電插頭和冷卻水插頭落下進行充電和冷卻液恒溫，水電插頭圓圈代表充電倉內電插頭和冷卻液插頭位置，方圈代表電池上對應的插座位置。

基于確認的定位策略，下一步需要分析容差結構、零件公差、水電插頭裝配等是否能滿足上述充電倉的關鍵尺寸功能。

3 分析電池進倉卡滯風險

電池進入充電倉如圖2所示，此時的關鍵尺寸就是電池長度尺寸和充電倉導軌間距尺寸，如果電池長度大于導軌間距，即會發生電池卡滯落不到位的問題。但也不能將電池導軌間距設計得過長，否則電池在倉內旋轉，影響水電插頭與電池匹配，故需要保證進倉的前提下，盡量收縮小電池和倉配合的間隙。

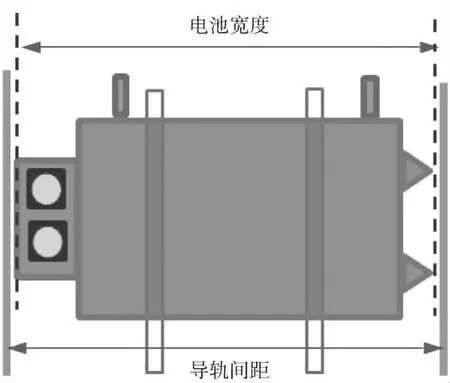
圖2 電池進倉示意

現有電池的初始長度公差2XX3+/-4 mm(公差值已做替換，非公司原始值，下同)，導軌間距的初始設計值是2XX6+/-1 mm，我們需要知道初始設計狀態是否存在電池干涉問題，如果有，概率是多少，以便進行風險評估和優化措施制定。此類計算主要有以下兩種方法。

3.1 概率分布函數法(一維尺寸鏈)

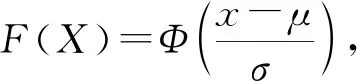
x0.000.010.020.030.040.050.060.070.080.092.10.98210.98260.98300.98340.98380.98420.98460.98500.98540.9857

為了簡化計算操作、提高效率和可視化，絕大部分汽車主機廠會采用一維尺寸鏈計算表進行快速計算(如圖4)。

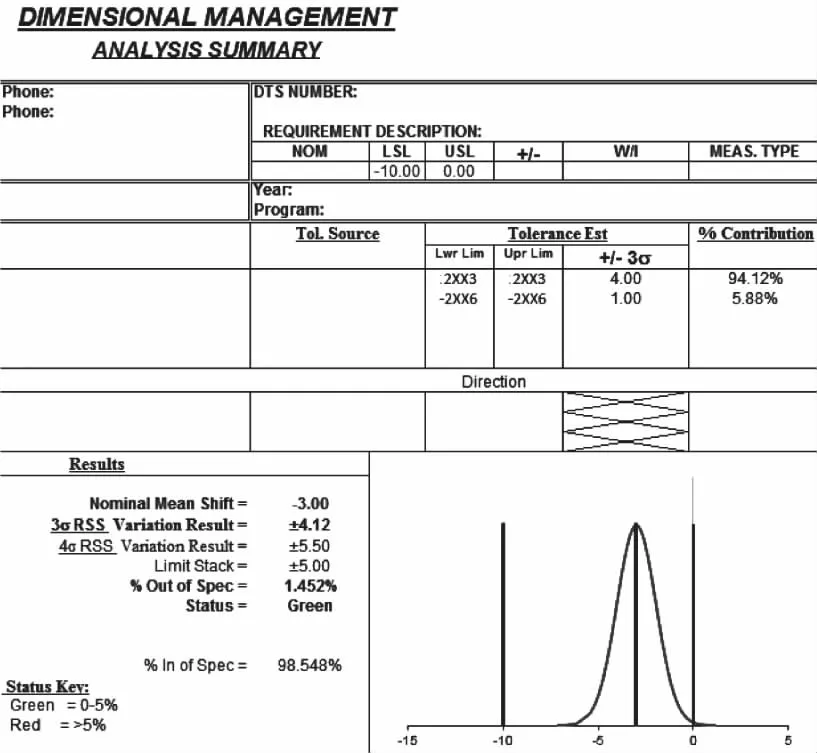
圖4 一維尺寸鏈計算表

該表主要運用了Excel函數NORMDIST等命令返回標準正態分布，繼而得到計算結果和正態分布可視化圖形。根據上段定義電池長度X小于導軌Y的概率為X-Y<0，將電池長度上下極限代入電池Nominal值2XX3，+/-3σ帶+/-4，導軌間距上下極限帶負數2XX6，+/-3σ帶+/-1，公差目標下極限為閾值-10，上極限為0，填入表格后可快速計算出合格率為98.548%，與采用查表結果基本一致，但效率更高，計算結果也更便于保存。

3.2 3DCS三維模型建模法

3DCS是基于蒙特卡洛(Monte Carlo)算法進行公差模擬分析，采用隨機模擬和統計試驗的方法求解，用該方法得到的結果比較符合實際生產情況[5]。

利用3DCS計算此干涉風險的步驟是：

第一步：在3D數模中將電池和導軌的定位點創建2×4個虛擬點(如圖5)，虛擬點pt1～pt4代表電池的匹配點，pt1′～pt4′代表導軌對應的點；

第二步：根據圖紙的公差定義，對上一步建立的8個虛擬點進行公差賦值；

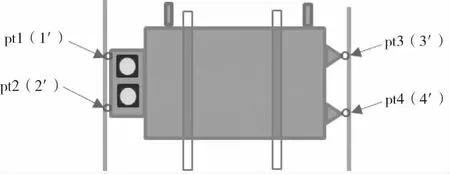
圖5 電池、導軌建點方式

第三步：創建測量，首先創建4個基礎測量，分別是電池后部外側端點至前部端面的長度，再采用軟件中的User DLL模塊“dcsMeasEq”，自定義對基礎測量項進行相應的數學計算，最后統計導軌外側和內側不能同時大于電池對應長度的概率即為超差概率，運行10000次，結果如圖6所示，超差率為1.82%。

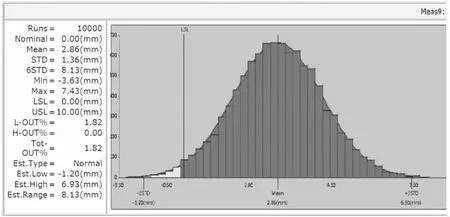
圖6 3DCS進倉干涉仿真結果

根據3DCS的計算結果，存在1.82%的電池尺寸大于充電倉的概率，根據換電站每天滿負荷上百次的換電次數，顯然此種狀態是不能接受的，根據團隊頭腦風暴，選擇了將電池長度和導軌間距公差分別優化至2XX2+/-2和2XX4.5+/-0.5，將優化后的公差用同樣方法帶入3DCS驗算得到的超差概率降低至圖7所示的0.02%，風險可控。

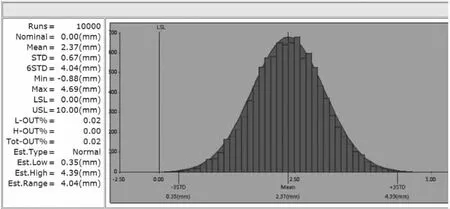
圖7 結果優化后

3.3 兩種方法對比小結

第一種概率分布函數法將電池尺寸和導軌尺寸在計算前已做最大最小處理，各當作一個參數進行線性計算，是一種簡化處理方式，采用基于此方法的一維尺寸鏈計算表易上手，在需要快速定性判斷問題時，推薦采用此方法。

第二種3DCS軟件分析方法，仿真程度最強，采用蒙特卡洛算法的偏差運算更接近實物狀態，結果更加可信。電池倉考慮到旋轉、平移及多目標，采用三維建模更加可靠。但由于需要較長的模型搭建時間，且對建模人員有較高的技術要求，故推薦在預測有一定風險或需要進行方案驗證時采用。

4 水電插頭裝配性分析

電池進入充電倉位后，還需要進行充電，在進行充電操作前，必須保證水電插頭能正常插入到電池對應的插座上，如圖8所示，尺寸偏差太大，容差系統不足，會造成系統報錯、無法充電的問題，將直接影響換電站的運行效率，故需要提前進行此功能區域的裝配性分析。

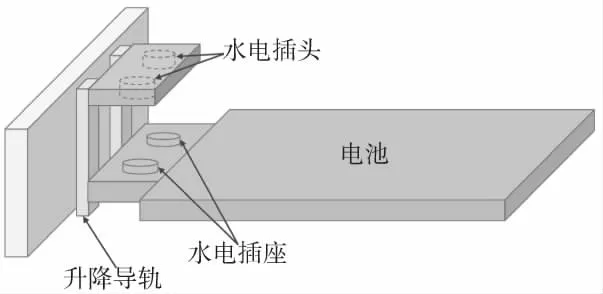
圖8 電池水電插頭插座示意

圖9 充電倉內實際位置示意

基于既定的定位策略及現場調研，我們確認了電池在倉內的位置為圖9所示兩種。

CASE1和CASE2兩種狀態分別代表電池在倉內真實存在的順時針和逆時針旋轉下的姿態，兩種姿態下會分別跟前部、后部的Y向限位塊接觸。接下來就需要基于3DCS對兩種姿態下的水電插頭裝配性進行分析。

第一步：根據定位策略與測量要求在對應的零件上建立DCS點，并賦公差；

第二步：新建兩個緊貼導軌虛擬夾具，此夾具的作用是讓電池在倉內可以均勻旋轉，虛擬夾具為4個裝配點，分別是單側電池和導軌匹配點的位置；

第三步：創建Move。

1)用six plane命令(如圖10)，將電池裝配至滑鏈、一側的導軌夾具和限位塊上；

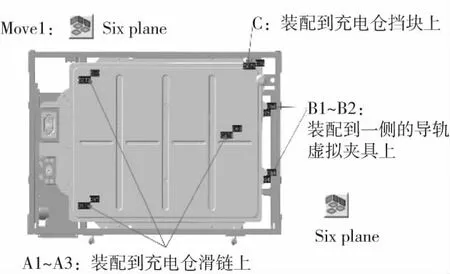
圖10 six plane move示意圖

2)用iteration命令中的旋轉迭代功能，將電池以O點為圓心進行順時針旋轉，停止條件是電池A點與左側導軌接觸(模型輸入間隙值≤0.01 mm)；

3)用iteration命令中的平移迭代功能，將電池包向下進行整體平移，停止條件是電池B點與限位塊間隙接觸(模型輸入間隙值≤0.01 mm)；操作以上Move，即可實現電池包的CASE1狀態的模擬，CASE2狀態的搭接操作對稱即可；

第四步：建模測量，包含迭代Move需要的過程測量和最終需要的水電插頭裝配性測量，其公差值取決于水電插頭部件的容差吸收量，既定的為+/-X mm。

以上步驟完成后，進行10000次虛擬裝配，得到以下仿真測量結果(圖11)。

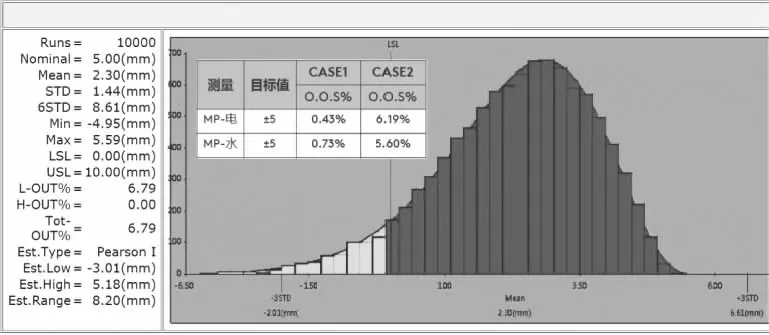
圖11 水電插頭裝配性計算結果

通過仿真結果可以看到，6.79%的超差率對于換電站的0.0X%的可接受失效率要求來說是不能接受的。針對存在的風險，經過團隊頭腦風暴討論優化方案。

方案一：將充電座進行多方向的隨型裝配，X向與電池前部的面進行貼合靠攏，Y向將電池左右側進行對中，虛擬驗證得到超差率為0.00%，見圖12。

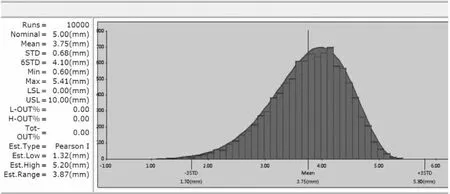
圖12 方案一：XY隨型機構計算結果

方案二：倉內的水電支架增加Y向對中機構，吸收電池旋轉導致的電池水電插座的位置偏差。帶入模型進行驗證，超差率為0.37%，見圖13。

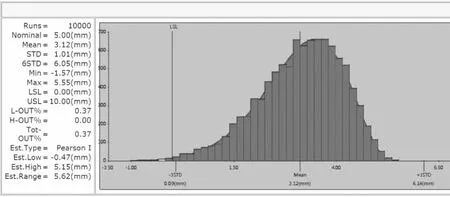
圖13 方案二：Y向對中結構計算結果

方案三：在不大幅增加成本的情況下增加水電插頭的容差吸收能力，從+/-X到+/-(X+1)mm。帶入模型進行驗證，結果如圖14，超差率2.38%。

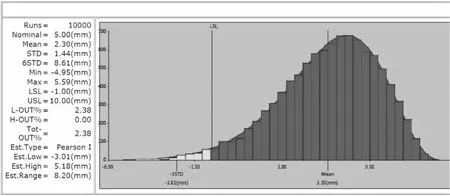
圖14 方案三：增加容差吸收能力計算結果

方案四：結合方案二和方案三，倉內的水電支架增加Y向對中機構，并適當增加容差量。帶入模型進行驗證，結果如圖15，超差率0.02%。

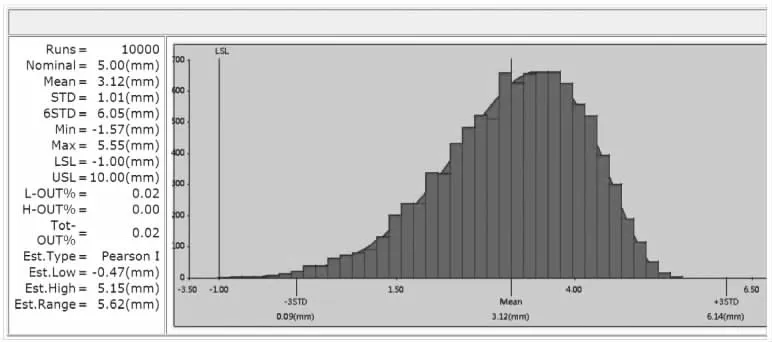
圖15 方案四：對中結構和增加容差結果

綜合評估四個方案：

方案一能夠100%滿足裝配要求，原理是降低尺寸鏈數量，采用局部裝配，對電池在倉內的姿態要求極低，可以減少電池與導軌公差，是一種最優的尺寸優化手段。但此方案需要較大的空間布置，對設備的結構要求很高，容易產生其他的失效模式，并將大幅提高換電站成本，綜合評估，暫不推薦。

方案二是簡化版的方案一，對機構的要求降低，且基本可以滿足現有空間的布置，但超差率為0.37%，不滿足0.0X%的可接受失效率。

方案三單純增加容差吸收能力，也是一種尺寸控制手段，但超差率為2.38%，不滿足0.0X%的可接受失效率。

方案四是方案二和方案三的結合，超差率為0.02%，滿足0.0X%的可接受失效率。

綜合對比評估后，方案四對于換電站充電倉的綜合收益更大，更值得采用。

5 結語

本文結合正態分布、3DCS等尺寸偏差分析工具，對電池包在換電站充電倉進倉過程、進倉后姿態進行準確的分析和有效的優化整改，其潛在風險點在換電站設計前期得以規避解決，更高效、更精準地推動換電站充電倉的設計。

隨著智能電動汽車的普及，各大傳統主機廠和新勢力公司對換電的需求越來越大，換電站的推廣和穩定運營離不開基本的尺寸理念和思考。