花崗巖殘積土邊坡強降雨入滲特性研究

張鑫

[摘? 要]：花崗巖殘積土邊坡在強降雨條件下，容易發生淺層土體溜坍、垮塌等水毀災害，而邊坡淺層土體降雨入滲特性對其產生機理及過程、規模起著關鍵性作用。文章建立了坡角為50°的三維邊坡流-固耦合數值模型，完成了暴雨條件下的飽和-非飽和滲流分析，得出了強降雨入滲特征及基于此的邊坡穩定特性。結果表明：隨降雨歷時的變化曲線上突變點。

[關鍵詞]：花崗巖殘積土邊坡; 強降雨入滲; 飽和-非飽和滲流 FLAC3D

TU45A

1 研究背景

我國華南地區分布有較廣泛的花崗巖殘積土邊坡，花崗巖殘積土顆粒間氧化物較易溶解，在降雨入滲過程中，其抗剪強度大幅降低。2020年8月中旬的強降雨導致我國多地遭遇50年一遇的洪水，造成多地地質災害。大量研究表明，降雨入滲是引發邊坡失穩的常見因素之一，隨著地表暫態飽和區的出現，土體自重增加，坡體穩定性降低。

鑒于FLAC3D平臺具有強大的內置FISH語言，為了充分發揮FLAC3D軟件在巖土工程分析的優勢，近年來關于基于FLAC3D模擬飽和-非飽和入滲的研究如火如荼。蔣中明等[1]通過自編FISH語言嘗試了基于FLAC3D平臺的飽和-非飽和滲流分析;劉杰等[2]基于有限元計算模型，觀察在不同初始表層基質吸力條件下，邊坡地下水位抬升過程。

本文基于有限差分滲流理論，研究強降雨條件下邊坡淺層土體的入滲特性，對花崗巖殘積土邊坡在強降雨條件下進行穩定性評價。

2 數值模型構建原理

2.1 花崗巖殘積土邊坡入滲模型

Lumb[3]在對香港地區花崗巖殘積土邊坡失穩的研究中首次提出濕潤鋒的定義，認為在強降雨（此處特指降雨強度大于土體飽和滲透系數）條件下，自坡表部位最早出現濕潤鋒，而后濕潤鋒逐漸向坡體內擴展。

2.2 水力曲線模型

針對土-水特征曲線，許多學者已經提出了多種計算模型，如：Van Genucheten模型[4]、Fendlund和Xing模型[5]。采用被廣泛應用的Fendlund和Xing模型對本文中花崗巖殘積土的土-水特征曲線進行模擬，即

θ=θslne+（φanm（1）

式中：θ為實時體積含水量; θs為飽和體積含水量;φ為孔隙水壓力;a、m、n為曲線擬合參數。

2.3 非飽和滲流實現原理

降雨入滲過程，遵循達西定律和質量守恒定律，達西流動方程如式（2）所示。

qi=-ksijwkrwxj（Pw-ρWxkgk）（2）

式中：qi為單位流量向量，ρw為流體密度，ks及kr分別為飽和及相對滲透系數。

在FLAC3D平臺中，認為飽和度變化計算的依據是流體體積微觀改變量的積累值，而這與飽和度的定義相一致，使得基于FLAC3D平臺開展滲流分析具備理論基礎。

在飽和滲流計算中，FLAC3D將節點上的飽和度內置為1，滲透系數強制置為飽和滲透系數，下一計算時刻孔隙水壓力：

1Mpt=-qi，i+qv-αεt（3）

式中：M和p分別表示比奧模量Pa和孔隙水壓力（Pa）; qi，i表示液體通量強度（1/s）; qv表示流體體積源強度; ε表示體積應變量; 在不考慮土顆粒的壓縮時，α取1。

基于FLAC3D平臺進行非飽和滲流計算中，將飽和度小于1的節點處的孔隙水壓力強置為0，飽和度s的更新公式為：

snpt=1s-qi，i+qv-αεt（4）

式中：n為孔隙率，其它符號意義同前。

2.4 降雨入滲邊界條件設置

本文預設的降雨條件下，滲流計算過程中需要實時監測入滲區表層單元的孔隙水壓力是否大于0，如果小于0（該土體單元未飽和） ，修改入滲邊界為流量已知邊界，流量輸入值為該單元的飽和滲透系數值，如果大于0（該土體單元達到飽和），修改入滲單元孔隙壓力為0。

3 算例

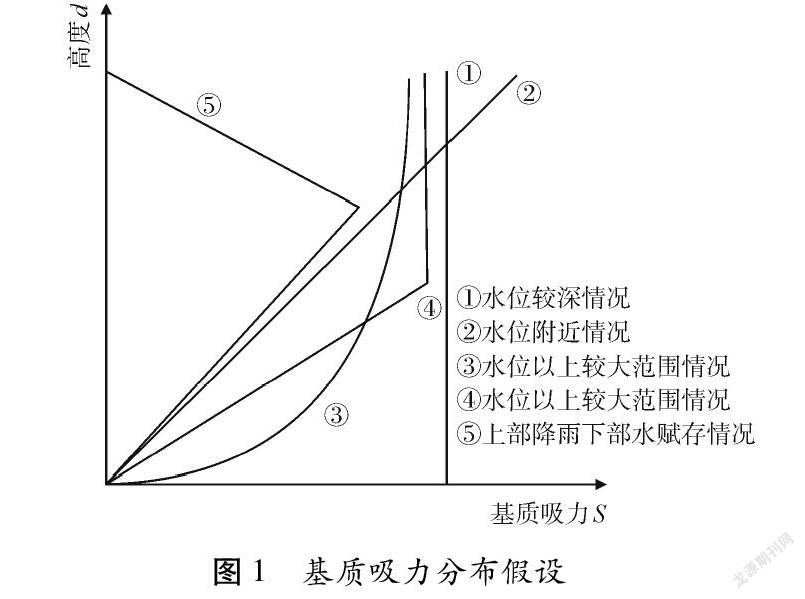
吳俊杰等[6]提出了關于初始狀態基質吸力分布的5種假設，如圖1所示，其中高度d為地下水面以上的豎向高度。

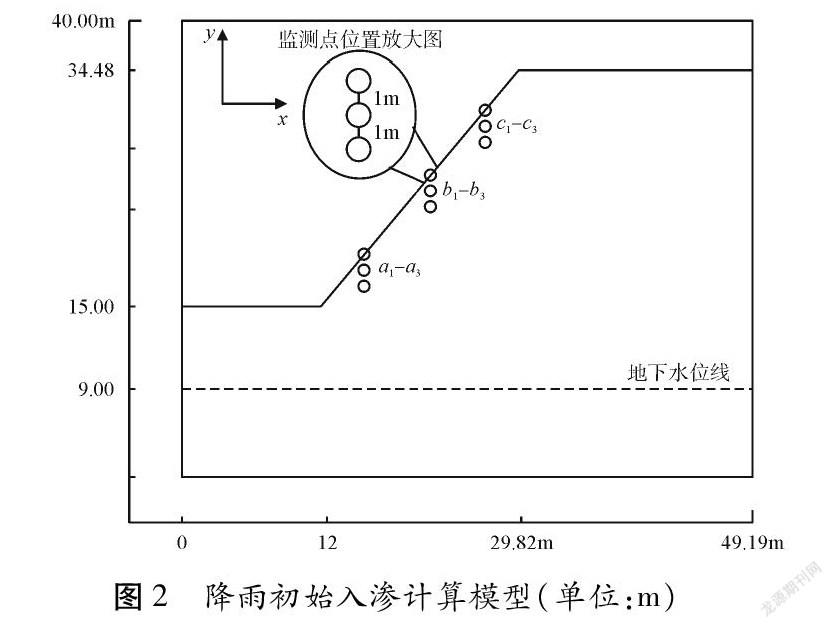
本文所建立的邊坡入滲物理模型如圖2所示，考慮到邊坡表面以及邊坡頂部區域是降雨入滲的集中作用位置，加之雨水沖刷、侵蝕邊坡的破壞作用是研究邊坡在降雨條件下穩定性的重要工作內容，基于此，在坡面設置a1、b1、c1 3個監測點，地表監測點下2 m范圍內設置等間距的2個監測點，邊坡共設置9個監測點。將坡面、坡腳及坡頂設置為入滲邊界，其他邊界均為不透水邊界。

所建立孔壓場的基質吸力先呈現線性變化而后達到一定高度后保持不變，符合曲線④表征長期為降雨邊坡基質吸力分布情況。初始滲流場分布如圖3所示。

初始滲流場建立后，首先進行彈性本構模型定義下的初始應力場計算，將位移和速度清零后，將其本構模型修改為Mohr-Coulomb模型后進行力學計算。在降雨過程中，對邊坡進行進行滲流計算及力學計算開具體降雨工況設置為0.012 8 m·h-1，連續降雨48 h。

參考文獻[7]相關數據，本文所采用花崗巖殘積土及土-水特征模型相關參數設置如表1所示。

3.1 滲流場變化分析

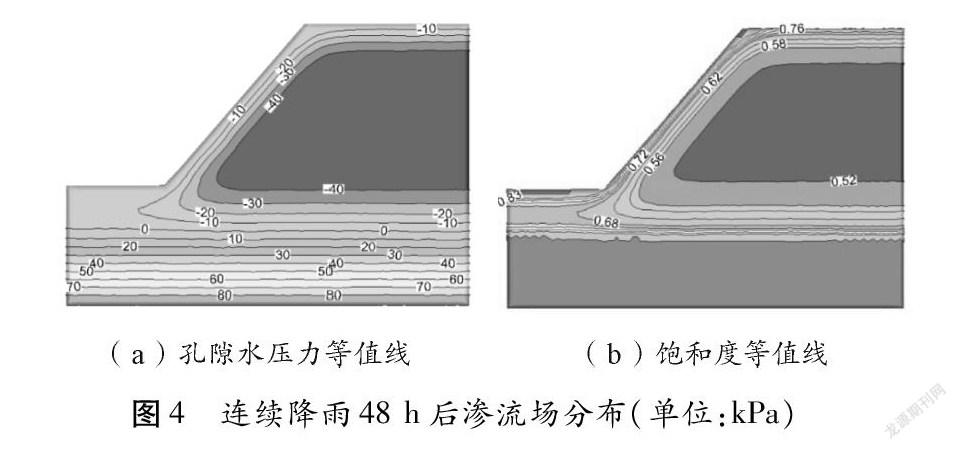
降雨結束的滲流場分布如圖4所示，可以發現，在降雨入滲過程中，邊坡上的暫態飽和區最初會發生在表層附近的土體中，暫態飽和區范圍逐漸向向內部擴展，且最終導致坡腳處的暫態飽和區范圍相比邊坡其他位置更大。邊坡預設監測點孔隙水壓力隨降雨歷時變化如圖5所示，由圖可知，邊坡坡面頂部、中部、底部各監測點負孔隙水壓力均逐漸呈消散趨勢，不同位置的特征點負孔壓對于降雨的響應也是不同的。坡腳處特征點孔壓變化較劇烈，坡面中部次之，坡頂處變化最慢。

3.2 穩定系數變化分析

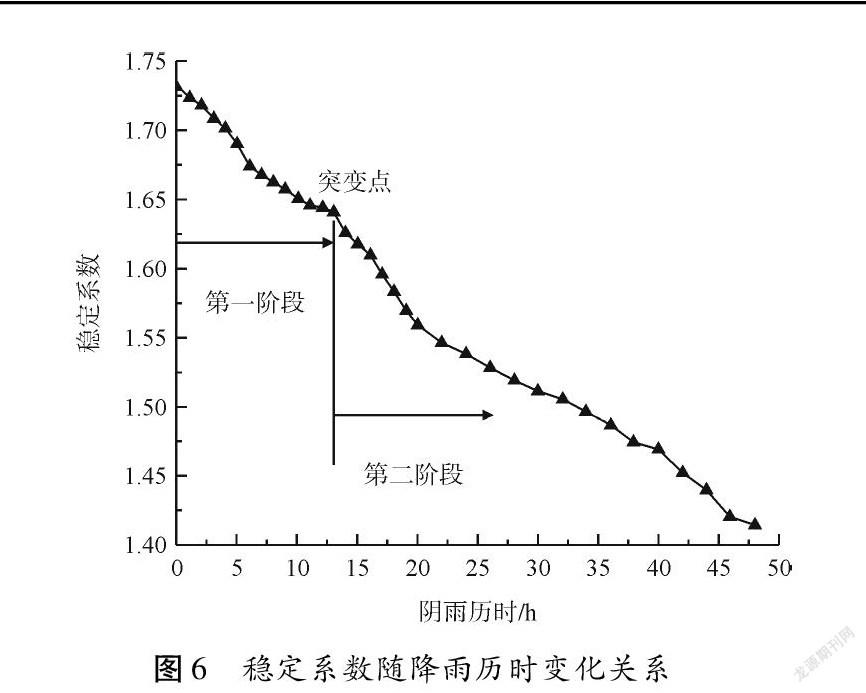
穩定系數隨降雨歷時變化如圖6所示，可以發現在降雨后，邊坡穩定系數均由初始條件的1.731下降到1.414，下降幅度為0.317，在降雨結束后邊坡已經處于相對不穩定的狀態。邊坡穩定系數變化過程呈現變化先快后慢的趨勢，隨后變化較平緩，在13 h處發生突變，再次開始快速降低，邊坡平緩階段持續時間較短，這也印證了邊坡降雨失穩階段主要發生在降雨后期，這一結論與文獻[8]結論相同。

3.3 位移場變化分析

前文對降雨作用下的邊坡滲流場變化進行了詳細分析，隨著土體孔隙壓力及飽和度的變化，土體力學特性也隨之改變。降雨結束的位移場分布如圖7所示，坡腳處水平位移及豎直位移都較為密集，意味著在此處已經發生了明顯的滑移，坡面中部沉降量更大，在邊坡防護工作中，應做好坡腳處排水設施的日常維護工作。

4 結論

（1）邊坡上各監測點孔隙壓力變化呈現的相似的入滲規律，坡腳處監測點孔壓變化的加速最為劇烈。

（2）在降雨入滲過程，穩定系數呈現降低趨勢;降低趨勢呈現先快后慢趨于平緩再迅速降低的特點，出現突變點的時

間在13 h附近。

（3）在實際工程支護設計工作中，應注意坡腳的排水處理設施的日常維護工作。

本文對花崗巖殘積土邊坡的降雨入滲過程進行模擬，對花崗巖殘積土降雨特性進行的研究為今后該方向研究和工程實踐提供參考依據。

參考文獻

[1] 蔣中明， 熊小虎， 曾鈴 基于FLAC～（3D）平臺的邊坡非飽和降雨入滲分析[J]. 巖土力學， 2014.35（3）：855-861.

[2] 劉杰， 曾鈴， 付宏淵， 等. 土質邊坡降雨入滲深度及飽和區變化規律[J].中南大學學報： 自然科學版， 2019， 50（2）：452-459.

[3] LUMB P. Effect of rain storms on slope stability [C]/ /Proceedings of the Symposium on Hong Kong Soils. Hong Kong， 1962： 537-552

[4] VANAPALLI S K， FREDLUND D G， PUFAHL D E， et al. Model for the prediction of shear strength with respect to soil suction[J]. Canadian Geotechnical Journal， 1996， 33（3）：379-392.

[5] FREDLUND D G， XING. A Equations for the soil-water characteristic curve[J]. Canadian Geotechnical Journal， 1994， 31（4）：521-532.

[6] 吳俊杰， 王成華， 李廣信. 非飽和土基質吸力對邊坡穩定的影響[J]. 巖土力學， 2004， 25（5）：732-736.

[7] ZHANG L L， ZHANG L M， TANG W H. Rainfall-induced slope failure considering variability of soil properties[J]. Géotechnique， 2015， 55（2）：183-188.

[8] 楊惺. 降雨條件下梅州花崗巖殘積土邊坡滲流及穩定性分析[D]. 廣州： 華南理工大學. 2019.