標準直齒圓柱齒輪輪齒任意點K 的齒厚計算

羅嘯峰

（四川職業技術學院 智能制造學院，四川 遂寧 629000）

引言

齒輪傳動是機械傳動各種類型中最重要的傳動形式[1]，應用非常廣泛。齒輪傳動的傳動精確度高，適應性廣，易于加工制造。與其他傳動形式相比，齒輪傳動具有的主要優點有：第一，傳遞功率、速度的范圍大。圓周速度可達300m/s，轉速可達105r/min，傳遞功率可從小于1W 到106W，齒輪直徑可由1mm 到150m 左右，能適應絕大多數工作場合下對傳動速度及傳動功率的不同要求；第二，傳動比準確，傳動精度高。齒輪傳動的傳動比無論是平均值還是瞬時值，理論上能保持恒定不變，這也是齒輪傳動獲得廣泛應用的原因之一，傳動過程中不存在彈性滑動或打滑，工作可靠性高；第三，傳動效率高，使用壽命長，能適應復雜工作條件的要求；第四，可傳遞空間任意夾角兩軸間的運動和動力，占用空間小，結構緊湊，可實現轉向改變和多級、多種傳動比的靈活變化；第五，制造和安裝精度要求較高[2],與帶傳動、鏈傳動相比，齒輪的制造及安裝精度要求高，價格較貴；第六，不適宜用于兩軸間距離較大的傳動。如圖1 所示。

圖1 齒輪傳動示意圖

1 齒輪傳動的基本要求

1.1 傳動比要求

傳動比恒定是對齒輪傳動的一個重要要求。齒輪傳動要求瞬時傳動比必須保持恒定不變[3]，否則，當主動輪等角速度回轉時，從動輪變速轉動，從而產生慣性力。這種慣性力會引起機器的振動和噪聲，影響其工作精度和使用壽命長。而齒輪齒廓線采用漸開線，保證了傳動比的恒定不變。如圖2 所示，外嚙合傳動中，O1、O2分別為兩齒輪的轉動中心，某瞬時兩齒廓在K 點處嚙合，兩齒輪運動時，必須滿足過嚙合點的公法線n—n上的分速度相等，否則將出現干涉或分離而不能傳動[4]。

圖2 外齒傳動嚙合點

上式表明，欲使齒輪保持恒定的傳動比，無論兩齒廓在任何位置接觸，過接觸點處的齒廓公法線都必須與連心線交于一固定點，根據漸開線的性質，漸開線上任意點的發生線，必與基圓相切，而該發生線為齒廓在該點處漸開線的法線。因此，當兩齒輪安裝位置確定后，兩齒輪齒廓無論在何處嚙合，過嚙合點的公法線必與兩齒輪基圓相切，即任意點嚙合時的公法線是唯一的，與兩齒輪的連心線交于固定的點P。因此，齒輪傳動能保證傳動比為恒定值。

1.2 傳動能力要求

在機械設施設備上，齒輪主要擔負著傳遞運動和動力的重要使命。因此，對齒輪的另一個重要要求，就是其傳動能力。齒輪的傳動能力，主要取決于齒輪的輪齒大小，即直接與齒輪的模數息息相關。在齒輪的承載能力設計時，齒輪的輪齒受載情況相當于一個懸臂梁，其齒根處的彎矩最大，所以必須要能夠準確計算其齒根厚度。

對齒輪的結構及應用的研究，一直以來都是非常廣泛而且深入的。齒輪的輪齒是齒輪傳動中直接承受載荷的主體，其形狀與尺寸決定著齒輪的承載能力、強度計算和加工制造。在齒輪設計過程中，準確計算齒輪任意位置齒厚，具有重要意義。在機械類專業高職教育教學過程中，有關齒輪基本尺寸計算，基本尺寸的最終結果化公式運算，而這些公式的計算推導過程比較欠缺，為了使同學們懂得計算公式的來龍去脈，公式的推導過程還是很有必要的。因此，本文從基本原理上，重點講解標準直齒圓柱齒輪任意位置齒厚的計算推導過程。

2 齒輪各部分名稱和基本參數

2.1 漸開線直齒圓柱齒輪各部分名稱

如圖3 所示，齒輪齒頂所在的圓周，稱為齒頂圓；齒根所在的圓周，稱為齒根圓；齒輪上具有標準模數和壓力角的位置所在的圓周，稱為分度圓，分度圓上的齒輪參數，是設計和計算齒輪基本尺寸的重要依據；齒輪上形成齒輪漸開線的圓周，稱為齒輪的基圓；分度圓到齒頂圓之間的徑向距離，稱為齒頂高；分度圓到齒根圓之間的徑向距離，稱為齒根高。

圖3 齒輪結構示意圖

2.2 漸開線直齒圓柱齒輪的基本參數

在齒輪的圓周上，輪齒的數量稱為齒輪的齒數，用字母符號z表示；為了計算的方便，將齒輪的齒距π等分并規定為簡單的有理數，稱為齒輪的模數，用字母符號m表示；齒輪分度圓上，法向壓力的方向與該點運動速度方向之間的夾角，稱為壓力角，用符號α表示，我國規定標準壓力角α= 20°。

由此，齒輪分度圓直徑d=mz，基圓直徑db=mzcosα，可見，當齒輪的m、z、α都確定時，齒輪的基圓直徑和漸開線形狀才確定下來，所以通常稱齒輪的模數、齒數和壓力角為齒輪的三大主參數。

工業生產中，齒輪的模數已形成標準系列，分第一系列和第二系列，選用時一般優先選用第一系列。齒輪模數如表1 所示。

表1 漸開線標準圓柱齒輪模數

3 基圓齒厚的推導計算

對于標準直齒圓柱齒輪，相鄰兩齒同側齒廓在分度圓上的圓弧線長度，稱為齒輪分度圓齒距，簡稱齒輪齒距，用P 表示。當直齒圓柱齒輪的齒數為Z 時，在分度圓周上，就有Z 個齒距P，即有：

在標準直齒圓柱齒輪上，分度圓齒距P 等于分度圓齒厚S 加上齒槽寬e，而分度圓上的齒厚S等于齒槽寬e，因此有：

對于同一個齒輪，齒輪輪齒不同部位的齒距是不同的，齒頂圓上的齒距最大，齒根圓上的齒距最小，從齒輪的齒頂圓到齒根圓，齒距大小逐漸減小；從齒輪的齒頂圓到齒根圓，齒厚由小逐漸增大，而齒槽寬由大逐漸減小，在分度圓上齒厚等于齒槽寬。

如圖4 所示，取齒輪的一個完整齒形，分度圓與輪齒左右齒廓交于B、G 兩點，D 為分度圓弧BG 的中點，基圓與左側齒廓漸開線交于點C，輪齒對稱線交基園于點E，B 點漸開線的法向壓力作用線與基圓相切于A 點。根據漸開線性質∠BOA=α=20°,圓弧BD 對應的圓心角設為γ，基圓弧AE 對應圓心角設為β，輪齒左側漸開線D 點處的展角為θ，設齒輪的模數為m,齒數為z，分度圓壓力角為α。分度圓齒厚即為BG 兩點間分度圓弧長，根據齒輪基本尺寸計算公式：

圖4 齒形結構

由漸開線的形成及特性可知，發生線沿基圓滾過的長度，等于該基圓上被滾過的弧長[6]。

輪齒左側漸開線與基圓交點為C，BD 段圓弧對應的圓心角為γ，圓弧AE 對應的圓心角為β，分度圓B 點的展角為θ。

4 漸開線函數

在（1）式中，tanα-α 與分度圓上漸開線的展角θ 有關。

在半徑為rb的基圓上，發生線繞基圓作純滾動，其切點由A 滾動到B 點時，發生線上與A 點相切的點，從A 點展開到K 點，如圖5 所示。設半徑為rb的基圓上漸開線任意點K 的展開角為θk，根據漸開線形成的基本性質，發生線BK 的直線長度等于基圓上被滾過的弧長AB，即：

圖5 基圖漸開線

由此可得分度圓展角方程為：

將展角方程代入（1）式，可得：

5 漸開線齒廓任意點K 處齒厚

對于標準直齒圓柱齒輪，由分度圓齒厚可推出基圓齒厚，在已知基圓齒厚的基礎上，又可以推導出漸開線任意圓周上齒厚的計算公式。

如圖6 所示，漸開線上任意點K 所在圓周與齒廓交于K、D 兩點，K 點壓力角為αk，半徑為RK,K 點展角為:

圖6 漸形線上任意K 點

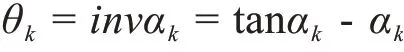
基圓齒厚所對應的圓心角假設為γ（弧度）

標準直齒圓柱齒輪漸開線任意點K 處的齒厚SK為：

6 齒根圓上齒厚分析

在標準直齒圓柱齒輪上，齒根圓直徑為：

而齒輪基圓直徑為：

設分度圓到基圓之間的徑向距離為hb，命名為齒基高，則：

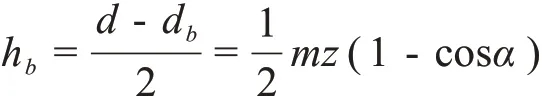
由上式可見，在標準直齒圓柱齒輪的模數一定時，齒基高與齒輪的齒數和標準壓力角有關，取標準直齒圓柱齒輪分度圓壓力角為標準值20°時，可求解出齒基高大于等于齒根高時齒輪的齒數為：

所以，當齒輪的齒數取42 個齒以上時，齒基高大于齒根高，即基圓直徑小于齒根圓直徑，此時，齒輪齒廓全齒高齒廓線皆為漸開線，齒根圓上的齒厚是可以計算的。

如圖7 所示，虛擬漸開線齒廓由基圓上B 點開始展開到齒根圓上A 點，齒根圓上A 點的漸開線發生線為AN，等于基圓上被滾過的弧長BN，設標準直齒圓柱齒輪齒根圓上的壓力角為αf，則角∠AON=αf，設齒根圓對應圓心角的一半為β，基圓對應的圓心角為γ，漸開線A 點的展角為θK，首先推導出齒根圓上的展角方程，即：

圖7 虛擬漸開線齒廓

所以，齒根圓上的展角方程為：

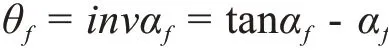
齒根圓對應的圓心角可計算如下：

由前述推導可知：

在標準直齒圓柱齒輪上，齒根圓的齒厚設為Sf，則有：

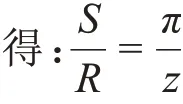
所以，齒根圓上齒厚計算公式為：

由圖6 可知：

在直齒圓柱齒輪齒根彎曲強度計算時，彎曲強度取決于齒根處的齒厚。在設計計算時，一對嚙合的齒輪，由于小齒輪的應力循環次數較多，齒根部位相對強度較弱，通常小齒輪在材料及熱處理方法選擇時，取齒面硬度比大齒輪高30～50HB，為了便于加工和裝配，小齒輪齒寬比大齒輪大5～10mm。由漸開線的性質可知，基園以內無漸開線。而對于齒數較少的直齒圓柱齒輪，齒根小于基圓，因此，在齒輪的基與齒根之間的齒廓線，不是漸開線，是由切削刀具頂端切出的過渡曲線，在齒輪嚙合傳動時，該段過渡曲線基本不參與嚙合，而是形成頂隙，起到防止齒頂卡住和儲存潤滑油的作用[7]。在一般的齒輪傳動設計中，小齒輪的齒數通常小于40 個齒，所以，靠近齒根處的齒廓線一般不是標準漸開線，其齒根處齒厚不易準確確定。鑒于此，當齒輪直徑較小時，其危險截面位置通常采用拋物線法和30°切線法確定，從而推導出了其成熟的計算公式。

7 輪齒不同位置齒厚比較

根據本文前述推導公式，可計算標準直齒圓柱齒輪不同位置齒厚，以比較其變化關系和作為設計計算的參考。下面以齒輪模數為3，標準壓力角為20°時，取不同齒數計算各位置處的齒厚，如表2 所示。

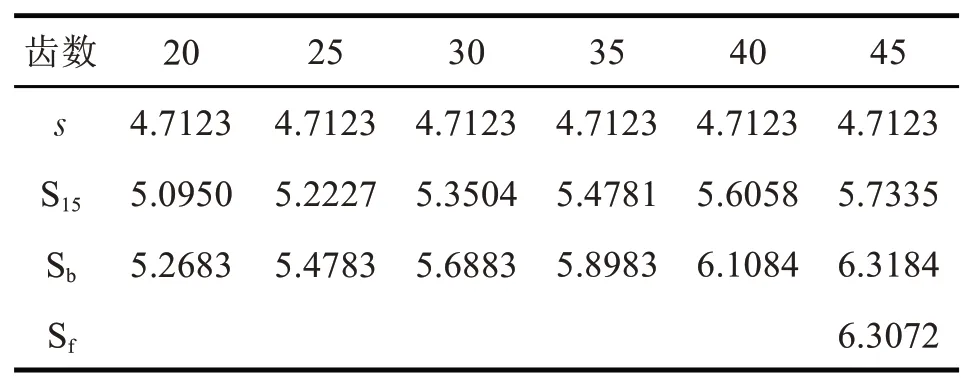
表2 m=3 時，各位置齒厚的對照表

由對照表可分析出，對于分度圓上同一模數和標準壓力角而不同齒數的齒輪，在同一位置處（分度圓除外），其齒厚隨齒數的增加而增大；對同一模數和齒數的齒輪，其不同位置齒厚，由齒頂向齒根方向逐漸增大[8]。

8 結語

在機械類專業高職教育教學過程中，有關齒輪基本尺寸計算，主要講解了分度圓齒厚的計算公式，而在例如公法線長度計算公式中，又涉及到了基圓齒厚，如下式，K 為跨齒數。

當跨過K 個齒測量時，公法線長度為K-1 個基圓齒距加上一個基圓齒厚。同時，針對齒厚的計算，也是齒輪承載能力設計計算的參考依據。因此，對標準直齒圓柱齒輪任意點的齒厚計算式的推導，以及進一步的把握和應用，具有重要意義。