基于曲線比較傳遞法推算水位精度分析

趙春城，于桂菊，汪連賀，張 岳，奉定平

(天津海事測繪中心，天津300220)

0 引言

JT/T 954-2014《沿海港口航道測量技術要求》[1]對利用歷史同步驗潮數據推算海中定點站潮位有如下規定：在相鄰兩水位站潮汐曲線相似性較強(即潮型數、日不等、漲落潮歷時等基本相同)的測區，可采用曲線比較傳遞法用于水位推算或缺測數據插補，并應符合下列要求。

數學傳遞模型如下：

Hx(t)=aHZ(t+b)+C

(1)

式中，Hx(t)為推算站的水位；HZ為基準站的實測水位；a為兩站的潮差比；b為兩水位站的潮時差；C為兩水位站的基面偏差。

確定關系值a、b、c可采用最小二乘法求解，通過離散格式的潮位值，對給定的初始a、b、c進行線性化，得到改正數矩陣，最終解算出關系值a、b、c的最優值，從而推算出推算站潮位[2]。

基準站與推算同步站同步水位數據時間長度不應少于7 d，參數計算使用水位數據時間長度不應少于3 d，符合精度檢測使用的水位數據時間長度不應少于3 d，符合精度觀測值與推算值之差的絕對值應滿足10 cm以內占總數的80%以上，20 cm以內占總數的95%以上，3020 cm以內占總數的100%的規定。文章嘗試利用上述原理采用青島港歷史同步驗潮數據推算海中定點站2021年潮位數據；因2011年和2016年均有實測潮位數據，2016年實測潮位能夠進行驗證2011年推算2016年潮位精度，從而能夠得到利用歷史數據推算2021年潮位的精度。

1 技術要求中的概念解釋

1.1 曲線相似性

若AB兩站在時間段N1，N2內進行同步觀測，兩站的水位采樣值分別為與時間相關的序列，X1，X2，X3，…，XN和Y1，Y2，Y3，…，YN，從離散數學原理可知，兩曲線的相似程度是由一定采樣值的相關系數決定；相關系數R公式為：

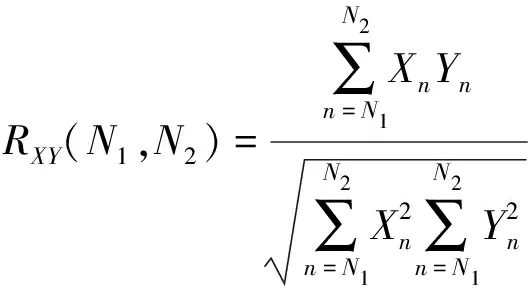
(2)

當R越接近1時，兩曲線越相似；當R接近0時，兩曲線不相似，所以R是兩曲線相似程度的度量。

1.2 潮型數

每個驗潮站調和分析出的2個全日分潮(K1、O1)和一個半日分潮(M2)的振幅有如下關系：

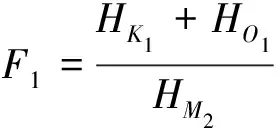
(3)

式中，F1為分潮平均振幅的比值；K1、O1為半日分潮；M2為全日分潮。根據式(3)將潮汐類型分為4類，當04.0為正規日潮。根據計算的潮型數值判斷潮汐性質，根據潮型數判斷潮型是否相近。

1.3 日不等

1 d中兩次高潮或低潮潮高不等現象，稱為日不等。日不等現象主要由月球赤緯變化產生，當月球在最北或最南附近時，所產生的日潮不等最大，此時潮汐稱為回歸潮。當月球在赤道附近，兩高潮潮高約相等，這時的潮汐稱為分點潮，此時月球大約處在春秋分點附近而得名。

在《沿海港口航道測量技術要求》中，根據潮型數和日不等及漲落潮歷時是否基本相同和曲線相似性的相關系數確定兩歷史潮位曲線能否用于潮位推算。

2 算例分析

文章的算例數據為青島港某港區2011年和2016年至今的部分長期驗潮站和海中定點站數據，該項目共涉及岸上潮位站1處取名為djk長期站，海上定點站2處，分別取名為hdz和hdw站。djk長期站和hdz站直線距離為18 km，hdz站和hdw站直線距離為13 km，3站均為歷史站點，2011年3站曾進行同步觀測，觀測日期為2011-04-29—2011-05-26，共28 d，3站潮汐性質相同，潮汐曲線相似性較強(即潮型數、日不等、漲落潮歷時等基本相同)，此次計算各站深度基準面確定值和潮型數統計出了28 d的潮型數，djk長期站為0.35，hdz站為0.36，hdw站潮型數為0.38，可見3站潮型數基本相同。

文章統計了2011-05-18—2011-05-20(低潮部分)3站日不等數據，18日djk站為85，而hdz站為87，hdw站為93；19日djk站為98，而hdz站為99，hdw站為99；20日djk站為86，而hdz站為87，hdw站為84；統計表明3站日不等基本相同。

經過對3站同步驗潮數據的計算和分析可知，3站潮型數基本相似，都是正規半日潮，日不等潮不等基本一致，3站漲落潮歷時都在6 h左右；對2011-05-18—2011-05-21的潮汐曲線進行相似性計算，得到海中兩定點推算站和djk長期站的相關系數，djk長期站與hdz站的相似系數為0.9，999，763，573，669，djk長期站與hdw站的相似系數為0.9，998，868，725，009，由潮型數、日不等、漲落潮歷時等基本相同可判斷出3站潮汐曲線相似性較強；因此能夠采用曲線比較傳遞法進行水位推算，即采用djk長期站推算海中定點站hdz和hdw站，本工程采用的同步數據為2011-05-18T00：00—2011-05-21T00：00，djk站與hdz站3 d的同步數據，分別計算潮汐曲線相似性相關系數，應用上述原理使用djk站的潮位根據曲線比較傳遞法推算相應hdz站同時間的潮位。

3 潮位推算精度驗證

為驗證潮汐模型推算潮位的可靠性，曾于2016-05-04—2016-05-17在海上定點站hdz站實拋水位儀，獲得13 d共1868個實測潮位數據，用以驗證推算潮位精度。此次驗證依然采用2011-05-18T00：00—2011-05-21T00：00 djk站和hdz站的同步數據，利用模型輸入djk站2016-05-07T00：00—2016-05-17T00：00分潮位，推算hdz站2016-05-07T00：00—2016-05-16T00：00分潮位，與hdz實測潮位進行比較。共比較1440個潮位數據，比較結果如表1所示。

表1 基于曲線比較傳遞法推算值與實測值差值統計

《沿海港口航道測量技術要求》對推算精度要求為：≤10 cm所占區間為≥80%；≤20 cm所占區間為≥95%；≤30 cm所占區間為≥100%。

經表1的統計比對可以看出，推算值與實測值差值≤10 cm的占比較樣本總數的100%，推算數值精度遠遠高于規范規定精度要求，表明采用2011年3站同步數據推算2016年海中定點站潮位是滿足精度要求的，因此利用2016年3站同步潮位推算2021年海中定點潮位是可行的。

由于hdz站的歷史潮位由djk長期站為基準經天文潮位加余水位的方式計算所得，因此也驗證了hdz站天文潮位加余水位推算潮位和實際觀測驗證推算的準確性，由djk站天文潮位加余水位的方式推算hdz站和實際觀測的2016-05-07—2016-05-16的1440個潮位比對如表2所示。可見基于曲線比較傳遞法推算hdz站精度在10 cm，精度較高；通過采用djk站采用曲線比較傳遞法推算hdz站經過對兩站抽樣進行精度驗證，完全能夠符合規范要求，證明該種方法推算潮位可以進行水深改正。

表2 基于余水位推算法推算潮位與實測潮位比對精度

4 結束語

文章利用2011-05-03的同步驗潮數據對2016年5月的海中定點潮位站進行了水位推算，經與實測潮位比較差值在10 cm之內，驗潮站最遠距離在50 km之內，推算時間間隔為5 a，嚴格按照技術要求操作的情況下推算潮位用于水深改正是能夠滿足精度要求的，因此可利用2016年潮位同步資料以岸上djk長期站推算海中定點站hdz站和hdw站2021年的潮位資料，5 a間隔精度能夠滿足測繪精度要求。同步曲線推算日期的選取與所推算的月份日期是否應該相同，歷史同步曲線與推算日期間隔是否有限定要求，用于推算水位精度驗證的時間較短能否得到普遍性的結論，這些問題仍需大量數據的驗證支持。