基于小波分析的月售電量預測方法

王梓屹，王越涵

(國網撫順供電公司，遼寧 撫順 113008)

1 概述

2020年，國家發展改革委、國家能源局聯合修訂印發《電力中長期交易基本規則》(發改能源規〔2020〕889號)。售電公司作為零售市場的主體，擔任著從市場購買電能，并出售給用戶的中間商角色。在電力交易過程中，售電公司面臨著市場價格和用戶側負荷雙重波動的風險。利用精確的月售電量預測結果制定合理的購售電策略來提高效益，是售電公司面臨的關鍵問題。因此，提高月售電量預測精度的研究具有重要意義[1-3]。

綜合國內外月售電量預測方法發現，售電公司普遍使用相對成熟可靠的時間序列法。但是模型本身存在缺點，時間序列適用于變化平穩、變化趨勢明顯的月售電量序列，如果直接對不平穩的月售電量時間序列進行預測，達不到預想的精度[4-13]。

本文在上述研究的基礎上提出了基于小波分析的灰色和自回歸移動平均(auto regressive integrated moving average，ARIMA)預測方法。

小波分析是一種變換方法，能夠通過小波變換提取出被分析量時域和頻域的信息用來分析，先將月售電量序列的逐月增長特性與隨機波動特性分解成2種子序列，此時非平穩的待預測月售電量序列就被分為增長特性子序列和平穩波動子序列這2種子序列。經過上述分解之后再針對這2種子序列的特點分別選取最適合的預測模型進行預測。通過對這2種子序列的預測結果進行小波重構，最后得到最終的預測結果。本文預測策略結構如圖1所示。

圖1 本文預測策略結構

2 小波分析在月售電量預測中的應用

2.1 小波分析概述

小波分析可以從數學角度和應用角度2個角度來看。小波分析既是包括函數空間、廣義函數、傅里葉分析、抽象調和分析這些的總結，又是工程應用上的突破。本文研究的月售電量序列可看成一種信號，這種信號既有時域部分又有頻域部分，所以使用小波分析勢在必行[9-13]。

2.2 小波分解與重構

基于Mallat得出的結論，其分解及重構思想：設Hjf為信號S在分辨率2j下的近似分量，那么Hjf就可以進一步分解為f在分辨率2j-1下的近似分量Hj-1f和位于分辨率2j-1與2j之間的細節分量Dj-1f，分解過程如圖2所示。

圖2 信號不同頻帶分解過程

由于每一次分解都經歷一次降采樣，而月售電量序列總長度不變，所以每次分解時候得到的近似序列和細節序列都要減小為原來的一半。

2.3 幾種常見的小波

表1介紹了幾種常見的小波。

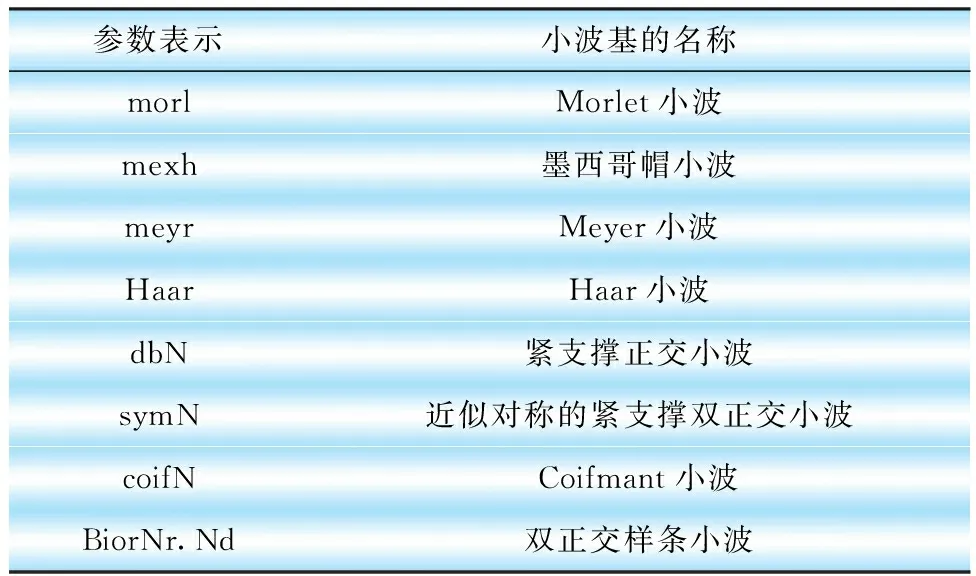
表1 MATLAB對應的小波函數

3 灰色與時間序列預測理論

3.1 灰色系統理論概述

1982年，中國學者鄧聚龍創造出了一種新的預測方法——灰理論。由于灰理論特別適用于數據特別少而且還不足夠明確的情況，所以適合月售電量的預測。灰色系統理論使用灰色模型(grey model，GM)進行預測，記GM(m,n)，表示對n個變量建立m階微分方程，可用于數列、災變、拓撲、系統預測等方面[4]。

3.2 時間序列理論概述

時間序列就是指數據按照時間順序排列的序列，是按照一定的時間間隔來排列的。月售電量就是一個典型的時間序列。1927年，G.U.Yule提出了自回歸(auto regressive，AR)模型，幾年后G.T.

Walker提出了移動平均(moving average，MA)模型和自回歸移動平均(auto regressive moving average，ARMA)模型。1970年，Box和Jenkin共同提出了整合ARIMA模型。ARMA模型是在AR模型和MA模型的基礎上增加了一個判斷模型的算式，但是局限于處理平穩數據；ARMA模型加入差分算法后得到ARIMA模型，能夠將非平穩序列變平穩，從而進行預測[4-16]。

4 案例仿真分析

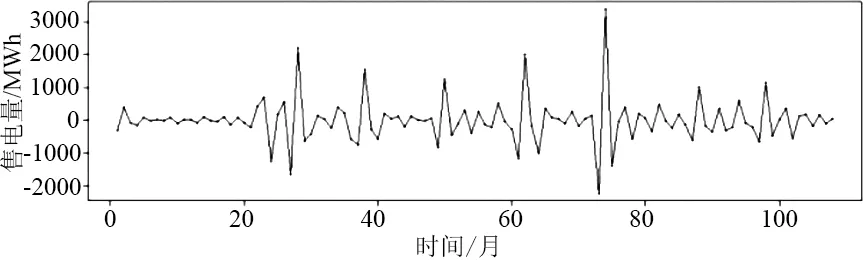
對實際案例進行分析預測，基于某市10年共120個月度月售電量數據，如圖3所示，以前108個月數據作為樣本，預測出12個月的數據，并提取出后12個月數據進行對比，得出模型的誤差進行分析探討。

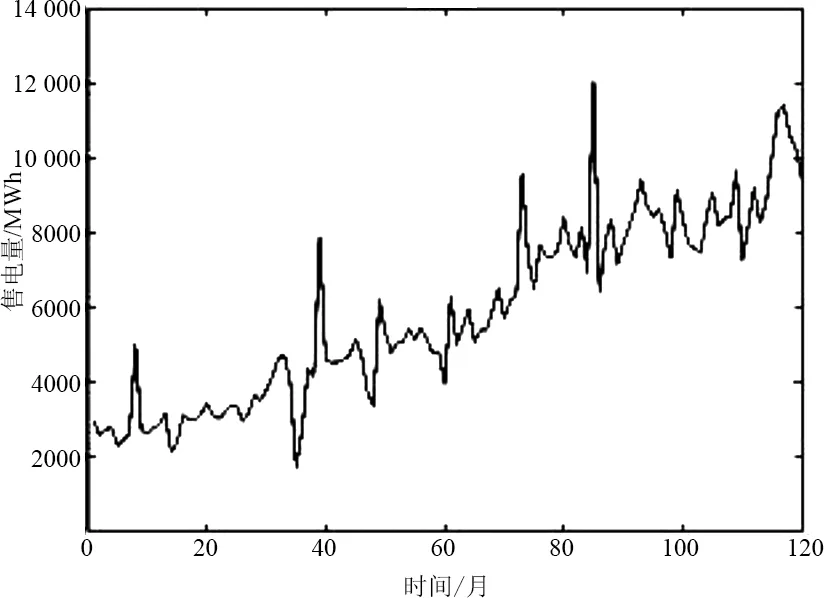
圖3 原月售電量曲線

預測誤差的大小是判斷預測方法優劣的根本依據，這里介紹4種常用的方法。

a.相對誤差

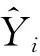
b.平均相對誤差

c.均方誤差

d.均方根誤差

本文將通過計算預測結果的相對誤差、平均相對誤差和均方根誤差來判斷預測模型的精度[8,11-13]。

4.1 小波分解

首先要確定小波基函數和需要分解的尺度，表2為各小波基特性比較，文獻[10-11]指出對于電力系統月售電量序列的增長和波動特性，采用近似對稱、光滑的緊支撐雙正交小波Daubechies作為小波基是合適的。

表2 小波基特性比較

表3為不同小波基分解的最大尺度，根據文獻[12]使用MATLAB自帶的Wmaxlev函數來確定最大分解尺度。

表3 分解的最大尺度

經過大量運算之后本文選取了db3作為小波基，并對月售電量序列進行3尺度分解。

圖4為分解流程，對某市120個月售電量數據進行上述小波分解，結果如圖5所示，得到6個細節分量和近似分量。由于ca2和cd2來自于ca1，而ca3和cd3來自于ca2，所以只需要預測出cd1、cd2、cd3和ca3即可。

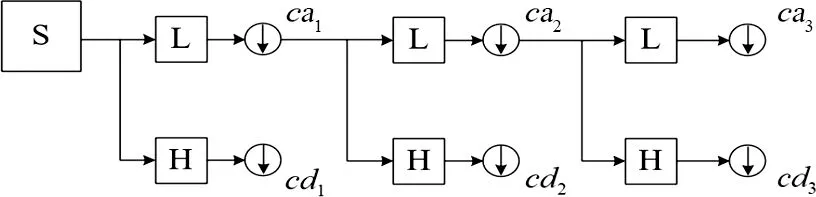
圖4 小波分解流程

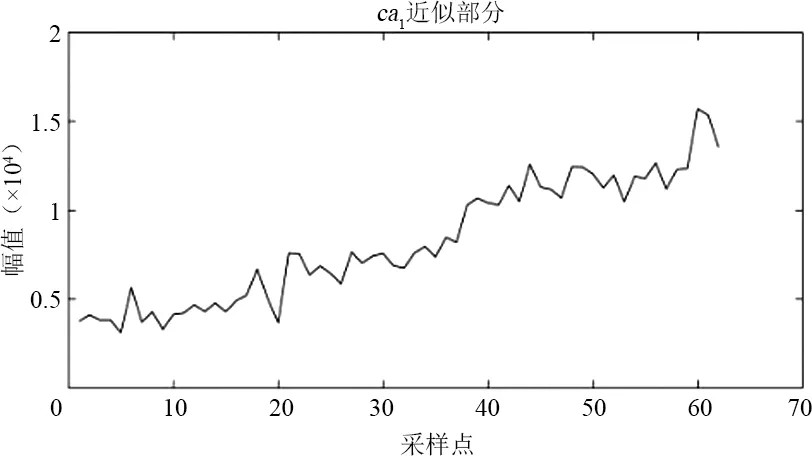
(a)

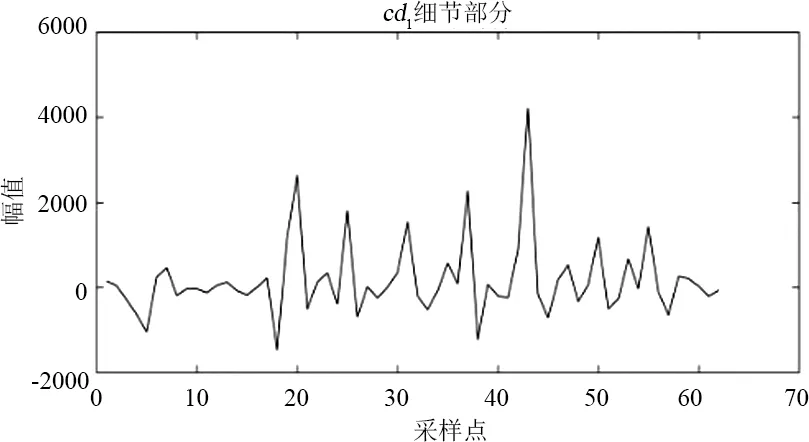
(b)

(c)

(d)

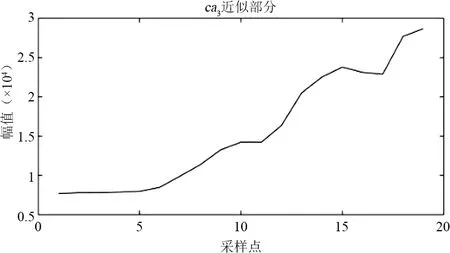
(e)

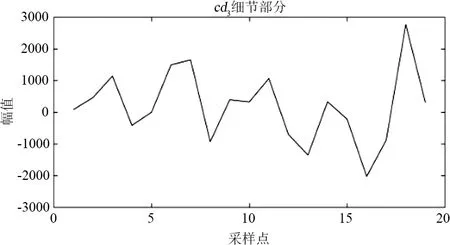
(f)圖5 小波分解結果

小波逆變換也叫做小波重構，正好與分解相反，首先進行升采樣，即為隔點插零。小波分解和重構的全過程如圖6所示。重構后4個分量直接相加可得總預測結果見式(1)。

S=d1+d2+d3+a3

(1)

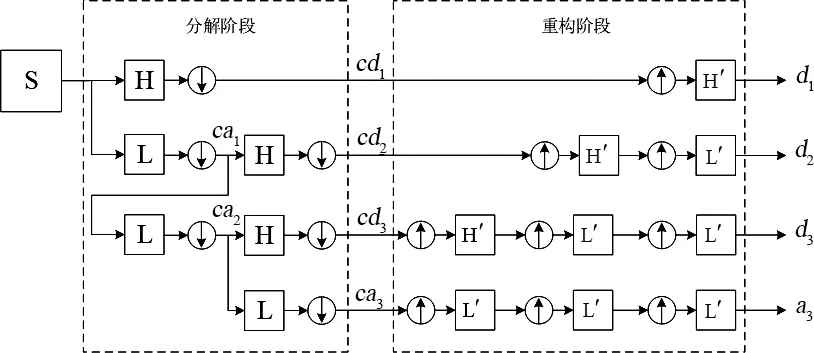
圖6 小波分解重構全過程

小波重構結果如圖7所示，從圖7可以看出，a3是近似分量也就是增長分量，代表著月售電量的增長特性，d1、d2和d3則為細節分量，也稱為波動分量，代表著月售電量的隨機波動特性。針對分解出的2組子序列的特點選擇了2種適合的預測模型。下面對a3進行灰色模型預測，對d1、d3和d3使用ARIMA模型進行預測。

(a)

(b)

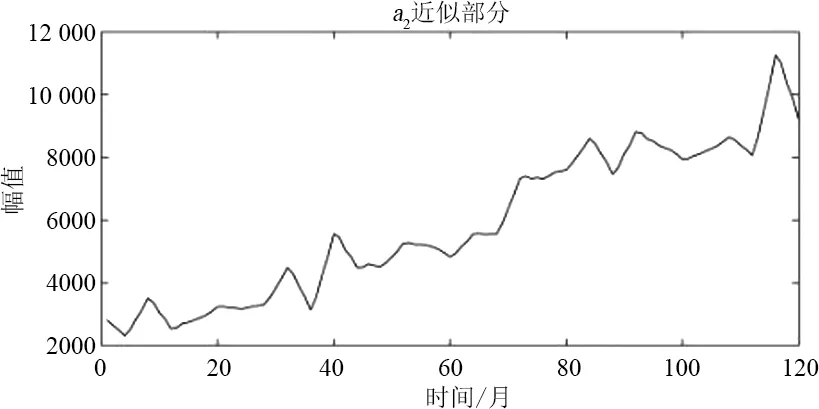
(c)

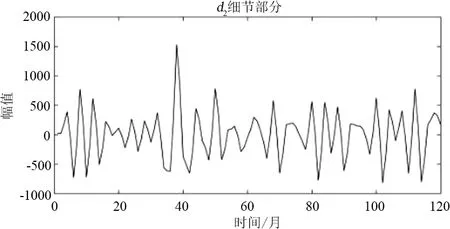
(d)

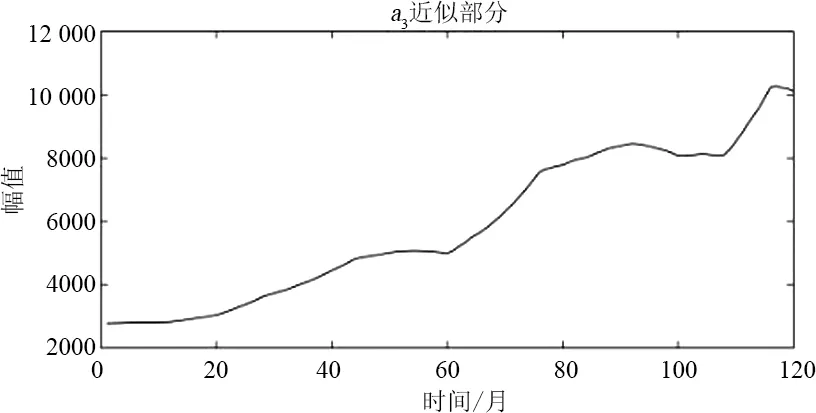
(e)

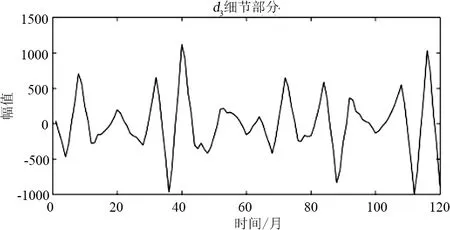
(f)圖7 小波重構后恢復原始長度的各分量

4.2 灰色預測

從a3中提取出108個數據作為輸入去進行預測，后12個作為結果進行預測分析，該灰色預測程序使用MATLAB來實現。預測結果如表4所示，結果比較如圖8所示。

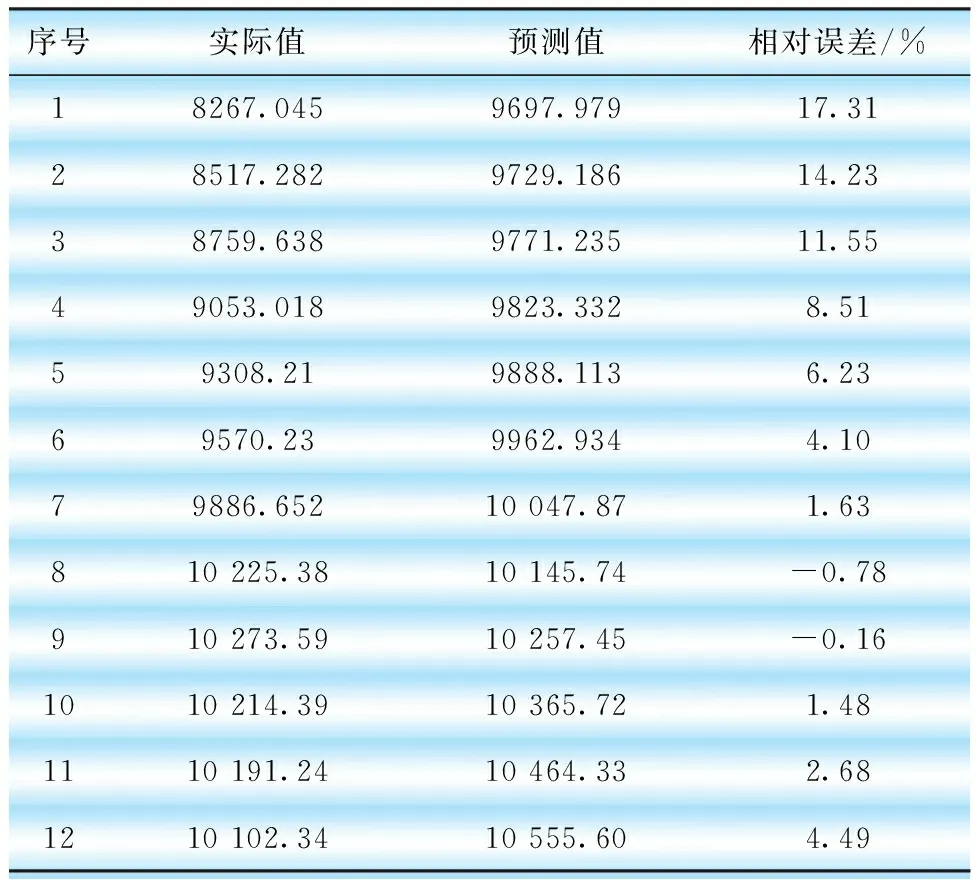
表4 近似分量a3預測結果

圖8 近似分量a3預測結果與實際月售電量的比較

4.3 ARIMA預測

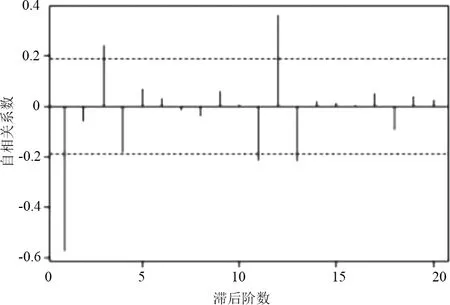
對細節分量d1、d2、d3進行ARIMA模型的預測，通過R語言軟件實現預測模型的編程。針對這3個分量，使用3個不同的ARIMA(p,d,q)模型進行預測，并分別進行比較，使用tsdisplay(x)函數生成圖像，結果如圖9—圖11所示。

從圖9中可以看出有許多滿足條件的模型，根據上文的介紹，通過計算AIC值，選擇這個值最小的1個模型用來預測。使用auto.arima(x,trace=T)命令自動計算AIC值并進行比較，結果顯示ARIMA(5,0,0)是最佳模型，AIC=1601.1。

(a)

(b)

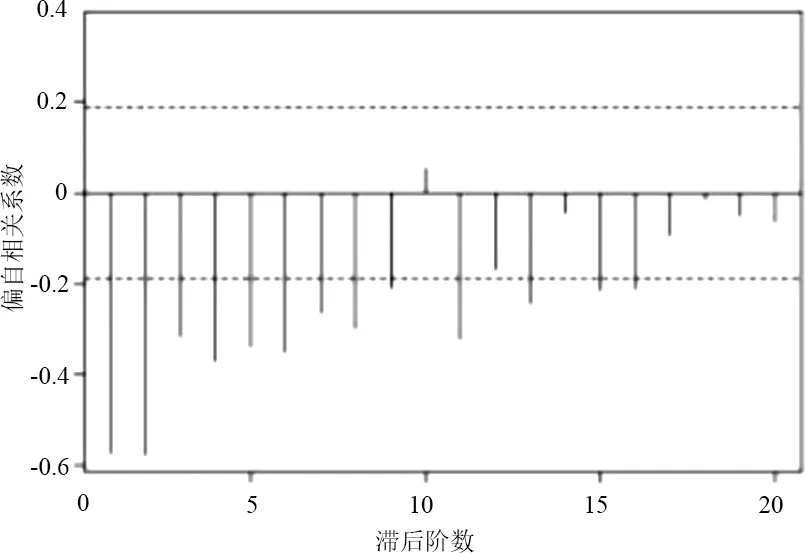
(c)圖9 d1的ACF與PACF圖

使用auto.arima(x,trace=T)命令自動計算AIC值并進行比較，圖10結果顯示ARIMA(4,0,0)是最佳模型，AIC=1445.92。

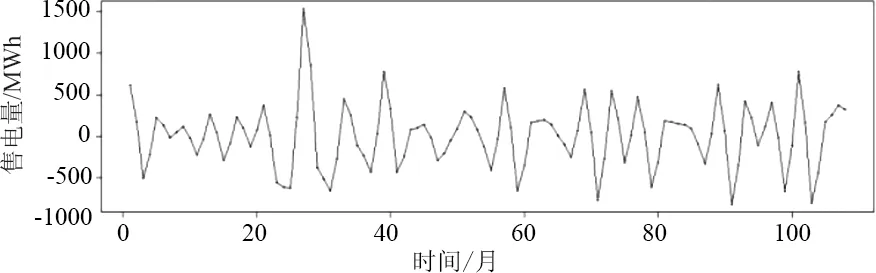
(a)

(b)

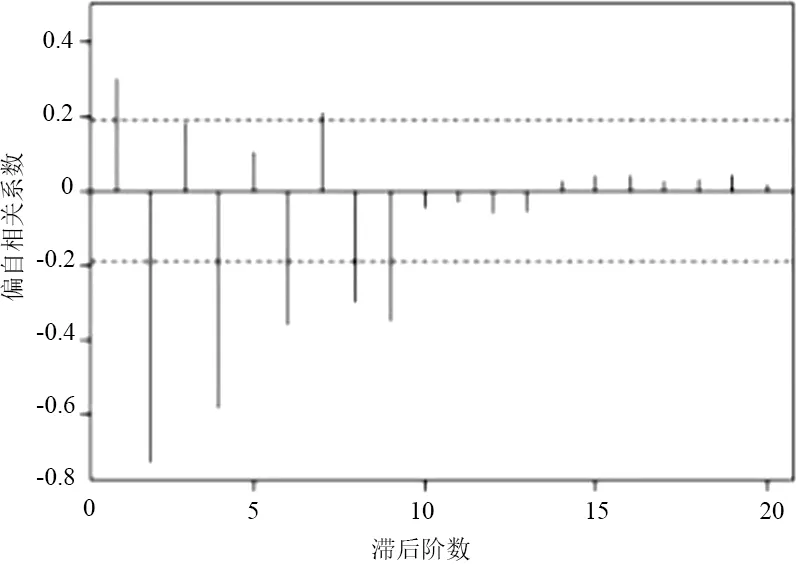
(c)圖10 d2的ACF與PACF圖

使用auto.arima(x,trace=T)命令自動計算AIC值并進行比較，圖11結果顯示ARIMA(5,0,0)是最佳模型，AIC=1370.07。

(a)

(b)

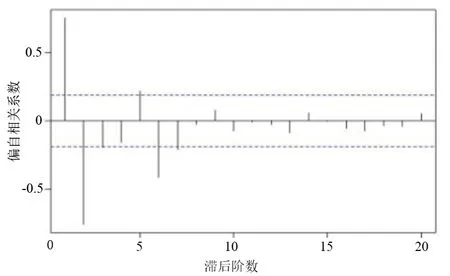
(c)圖11 d3的ACF與PACF圖

模型確定之后進行預測。為保證準確性，本文用1～108個月的月售電量去預測第109個月的月售電量，用2～109個月的月售電量去預測第110個月的月售電量。依此類推，每一個子序列進行12次計算得到下邊的結果。預測的結果如表5—表7、圖12—圖14所示。

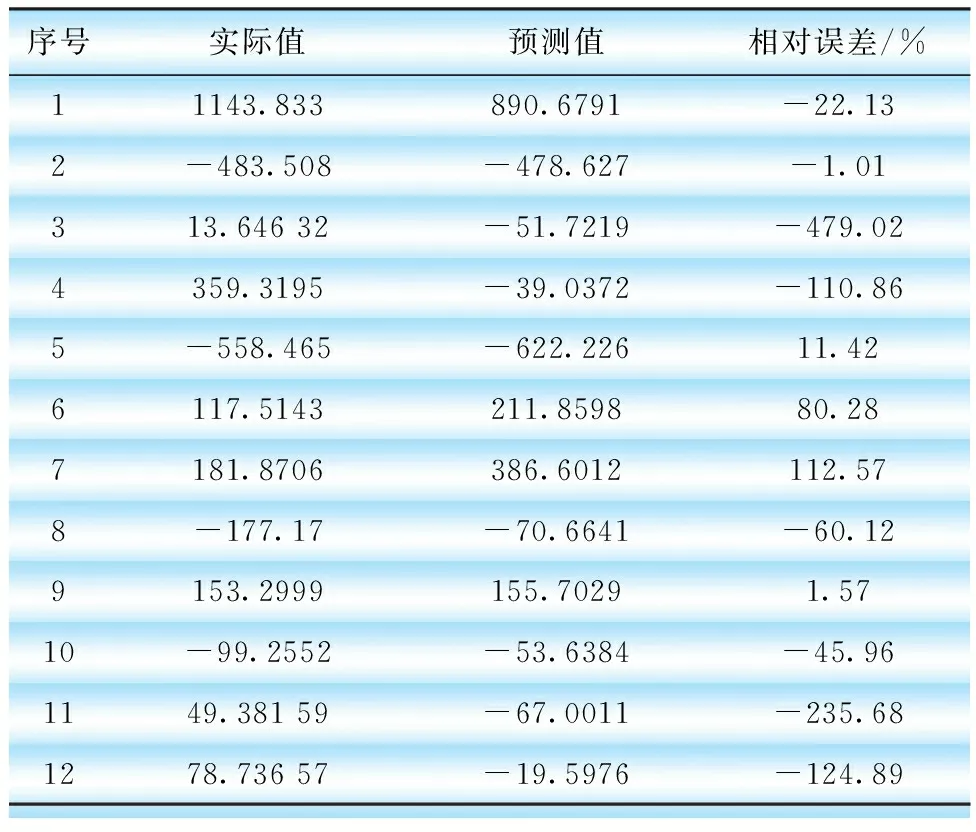
表5 細節分量d1預測結果ARIMA(5,0,0)

表6 細節分量d2預測結果ARIMA(4,0,0)

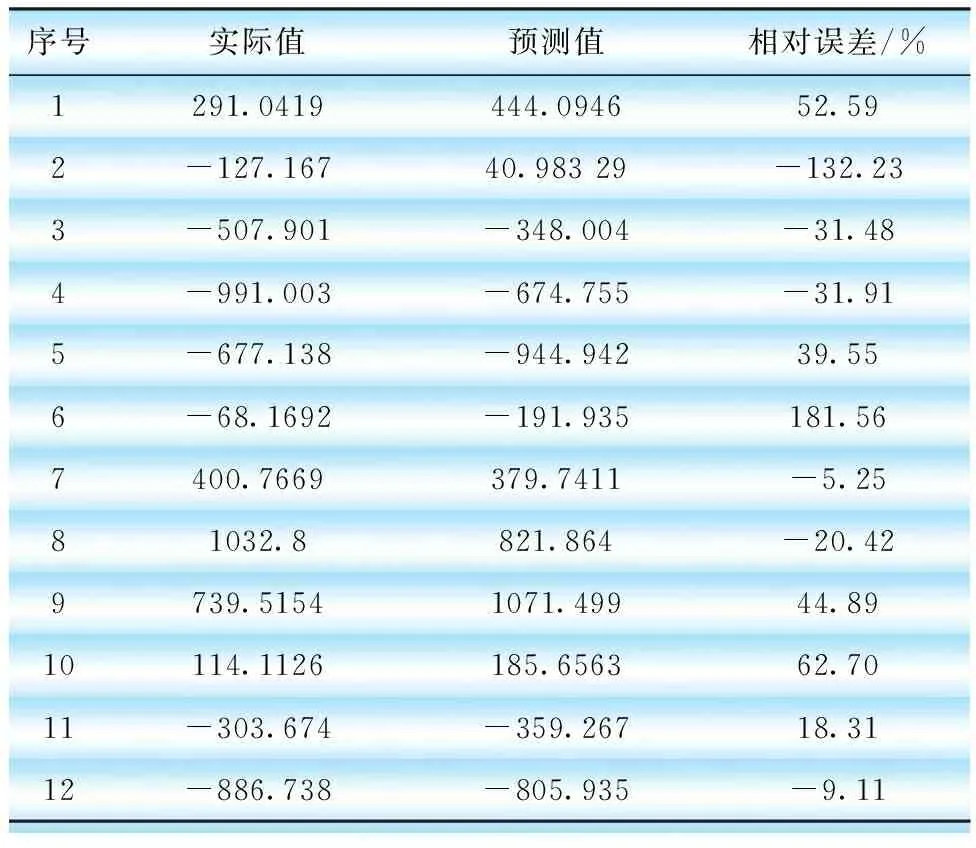
表7 細節分量d3預測結果ARIMA(5,0,0)

圖12 細節分量d1預測結果與實際月售電量的比較

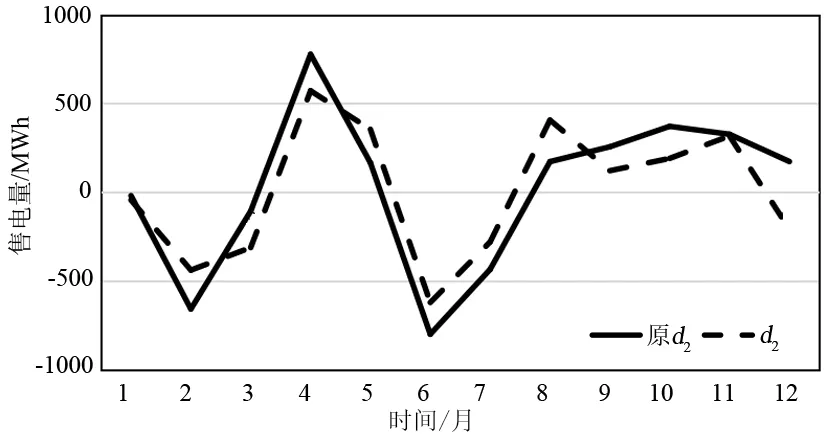
圖13 細節分量d2預測結果與實際月售電量的比較

圖14 細節分量d3預測結果與實際月售電量的比較

4.4 小波重構及誤差分析

根據小波分解與重構，由式(1)可知，將預測出的4個結果直接進行相加運算就能得到最終預測結果，結果如圖15、圖16、表8—表10所示。

圖15 負荷預測結果

圖16 各個預測模型結果比較

表8 預測結果

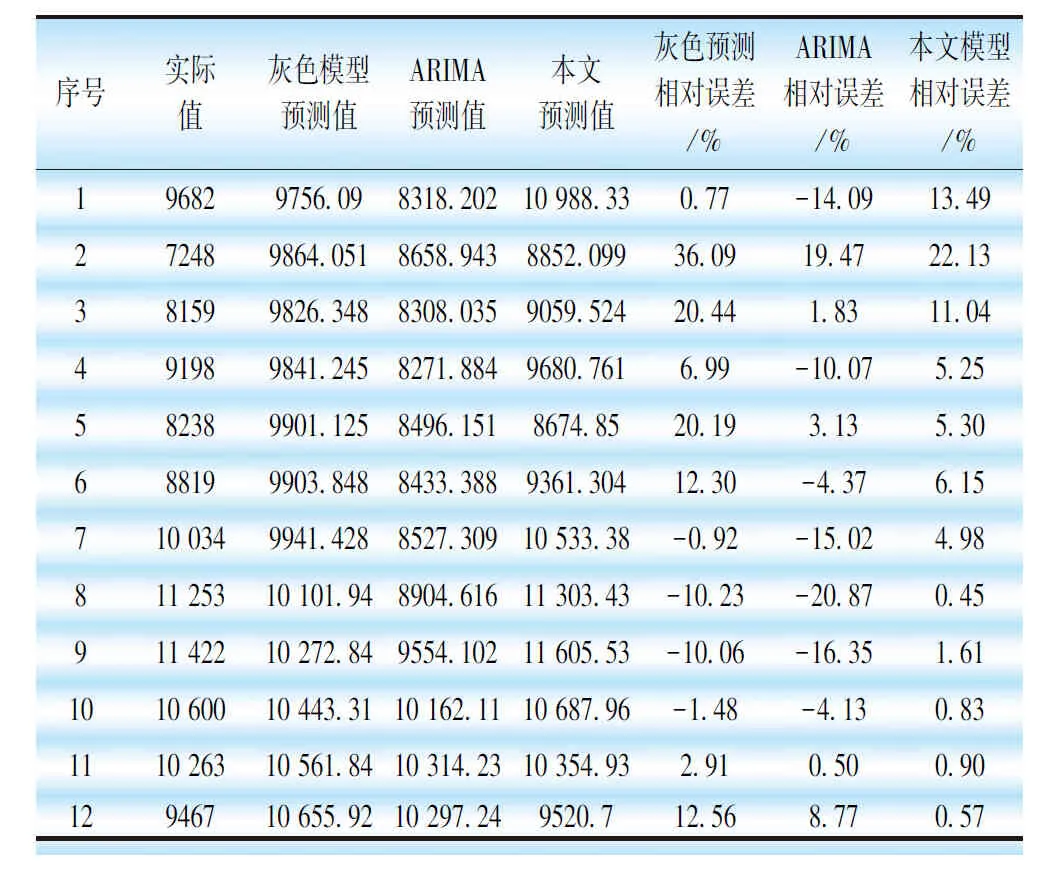
表9 本文方法與灰色或ARIMA單獨預測比較

表10 本文方法與灰色或ARIMA單獨預測比較

為了驗證本文構建模型的精度，進行了實例仿真分析，通過前108個月售電量數據預測后12個月的月售電量，預測結果見表8，繪出預測結果曲線見圖15。計算12個相對誤差和平均相對誤差見表9。誤差分析結果顯示，最大誤差出現在2月，為22.13%，最小誤差出現在8月，為0.45%，而平均相對誤差為6.06%，低于10%，誤差很小。為了進一步驗證進行小波分析的有效性，使用灰色預測模型和ARIMA模型各自進行單獨預測，并與本文模型進行比較，比較結果見表10和圖16，結果顯示灰色預測和ARIMA的最大誤差分別為36.09%、-20.87%。最小誤差分別為0.77%、0.50%，平均相對誤差分別為11.24%、9.88%。

通過以上比較表明了本文提出的小波分析能夠有效提高預測精度，并支撐售電公司制定合理的購售電策略，提高經濟效益。

5 結語

本文首先介紹了月售電量預測的特點，重點介紹了國內外現有月售電量預測方法和研究現狀，并分析探討了這些方法的優缺點以及使用條件，在此基礎上提出了一種基于小波分析的月售電量預測方法。小波分析并不是一種直接預測，而是一種分解重構思路，月售電量序列中同時具有逐月增長特征和隨機波動特征，直接進行預測無法獲得準確結果。通過小波分析將這2種特征分成具有單獨的逐月增長特征子序列和隨機波動特征子序列，然后再選取模型進行預測，最后將結果相加就會得到最終的預測結果。

本文成功編寫出MATLAB小波分解與重構程序，能夠對月售電量序列進行分解與重構；對增長特征子序列選取了灰色預測模型，通過編寫MATLAB灰色預測程序，能夠對增長特性的子序列進行預測；對隨機波動特征子序列選取了時間序列-ARIMA預測模型，編寫出R語言時間序列-ARIMA預測模型，能夠對平穩波動子序列進行預測。

最后通過仿真并對其進行誤差分析發現：對小波分解之后的預測結果與不進行小波分解而直接用這2種預測方法進行預測的結果比較，結果顯示采用了小波分解這一過程之后預測的結果更為準確，誤差更小，精度更高，表明了對月售電量序列進行小波分解之后再預測能有效提高預測精度，能夠解決售電公司預測精度的問題。