宗地面積量算中圓弧線段數據轉換處理方法
王俊
(合肥市測繪設計研究院,安徽 合肥 230000)
1 引 言
宗地面積量算工作中所得到的面積數據是土地調查、權籍發證、合理分配土地、收取土地出讓租費的依據,同時也是土地利用規劃、土地地類調查及土地整理等重要數據,面積量算經登記后具有法律效力,因此土地面積量算的正確性十分重要[1]。
建設用地四址邊界由規劃部門依據路網規劃設計確定,而路網規劃設計中存在大量圓曲線設計,這導致規劃用地測繪時許多地塊界線為圓弧線,辦理權籍登記時需要宗地勘界測繪,因規劃地塊邊界有圓曲線無法進入土地登記權籍數據庫,在出具宗地勘界圖時必須進行圓弧線段折線化方能權籍登記。此外,城市地籍測量權屬發證面積采用界址點坐標法計算,不能簡單地按圓弧線計算,兩種不同計算方法必然導致面積差異致使面積不準確[2]。
如圖1,規劃批準的A地塊西界規劃道路紅線為圓曲線,而權籍登記是按《土地勘測定界規程》依據界址點坐標計算面積,需對該圓弧段進行分段處理、即圓弧折線化;圖1中地塊A規劃設計階段面積按扇形計算、土地權籍勘測按三角形計算面積,由于計算方法的不同使得兩次面積計算有偏差[3]。本文從合肥市測繪設計研究院土地權籍測量工作實踐,運用解析幾何方法建立圓弧線折線化的計算模型,綜合考慮規劃設計和土地面積勘界均主要使用AutoCAD現狀,使用AutoLISP語言二次開發,實現快速、有效宗地面積計算,確保權籍勘界面積計算精度的符合性。

圖1 某帶圓弧線審批的地塊圖
2 折線化處理方法
2.1 面積偏差分析
規劃設計地塊面積按扇形計算、土地勘界按三角形計算面積,兩次面積計算有偏差[4],偏差部分如圖2所示,誤差面積為△,由圖可知,曲線上加密分段點越多就越接近圓曲線,三角形累計面積則越接近實際圓弧面積。

圖2 面積誤差分析圖
2.2 折線化數學模型建立
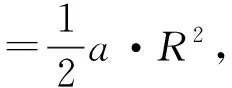

圖3 面積計算模型圖

(1)
當弧段分割成三角形越多(見圖2),偏差的面積越小;設圓弧平均分割n段,則得到:
(2)

(3)
(3)式可轉化成當n趨向∞時,求該式的極限。因
可得到:
(4)

(5)
有式(5)可知在無限分割圓弧段時,在界址點無限多時按宗地界址點計算的面積與按圓弧計算的設計圖形面積相等。顯然AutoCAD計算面積時是無法做到無限分割的,n越大圓弧折線界址點越多,則按界址點計算面積偏差越少,但不利于編制宗地圖和界址點坐標表;有必要確定合理的n值,使得n·△在允許的偏差范圍內,進而在滿足面積誤差精度要求下確定合理的折線化點位數。
2.3 模型中分段數n解算
城市建設開發建設中宗地權籍勘測均采用數字化測繪,界址點坐標單位采用米保留三位小數,地塊面積單位采用平方米保留兩位小數。以宗地圖內凸圓弧為例,由圖2可知整個扇形面積:
S扇=n·S△+n·△
(6)
式中S扇為規劃批準面積、n·△為缺失面積,該S扇為按圓曲線計算得到的圖形面積,計算時按照四舍五入法則對S扇面積小數位第三位取舍或進位,從而達到面積保留兩位小數的精度。
對式(6)解算n時,n·S△為精確面積,分析S扇圖形面積和進位對數學精度的影響,設面積S扇=××××.abc平方米:
當c≥5(c=5、6、7、8、9)時,n·△≤c-5
(7)
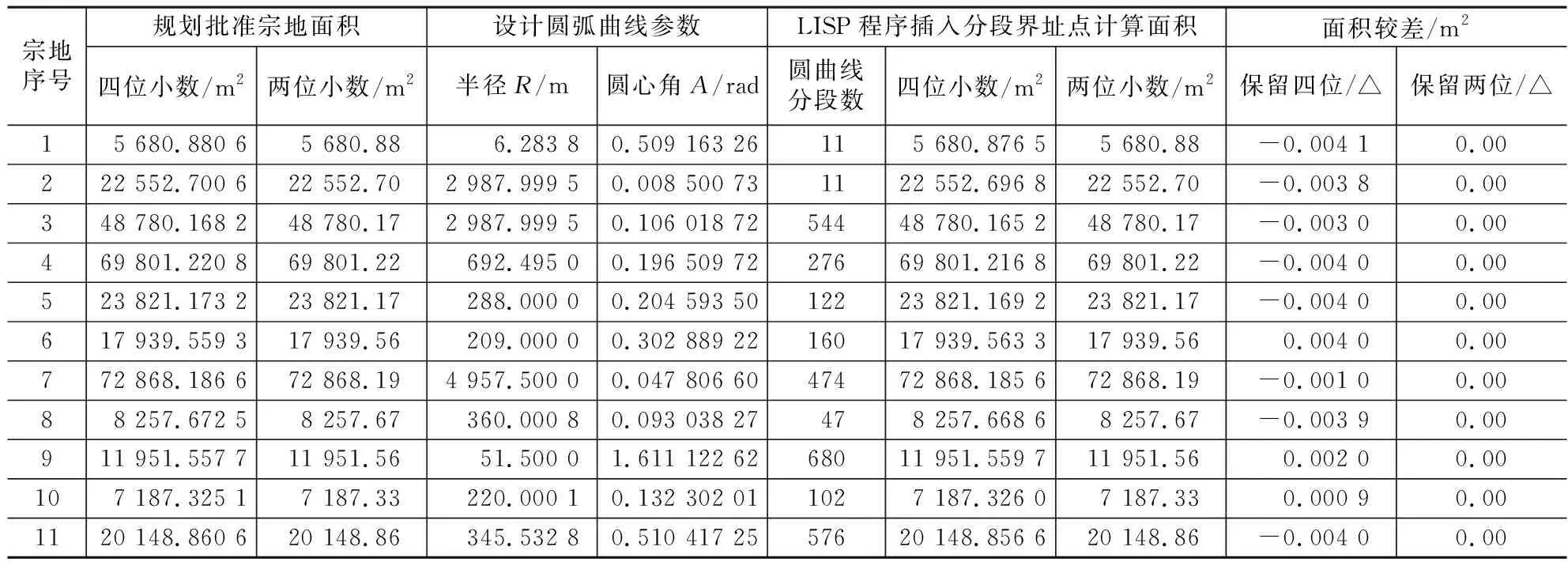
當c<5(c=0、1、2、3、4)時,n·△ (8) 在宗地圖內圓曲線為凹圓弧時,式(6)中n·△為增加面積。解算n時,n·S△為精確面積,分析S扇圖形面積和進位對數學精度的影響,設面積S扇=××××.abc平方米: 當c≥5(c=5、6、7、8、9)時,n·△≤14-c (9) 當c<5(c=0、1、2、3、4)時,n·△<5-c (10) 綜上所述當c≥5時,聯立不等式(7)、式(9)成立解得: n·△≤c-5,c≥5(c=5、6、7、8、9) (11) 聯立不等式(8)、式(10)成立解得: n·△<5-c,c<5(c=0、1、2、3、4) (12) 依據式(11)、式(12),為了解得最優等分段數n,建立不等式: (13) 式(13)中c為折線化前宗地面積有效小數位數的下一位數。規劃批準的設計地塊,其面積、圓弧半徑、圓心角及面積精度都是確定的,按該式解算出n、并據此設定折線段界址點計算的面積與S扇面積數學精度一致,該不等式可采用程序循環趨近法計算出滿足式(13)的n值,得到的整數n即為圓曲線折線化最優分段數,如果采用泰勒級數展開式計算n,則該分段數為n=[n]+1。 解算出弧線折線化最優分段數n后,利用設計圖形中弧線圓心坐標、弧段圓心角A、弧長及半徑R作為輸入數據,分別計算起始方位角aoB及各折線段轉角β,按下式得出圓弧各分段界址點坐標。起始方位角aoB可通過圖形圓心坐標和圓弧起點(按順時針法則確定)坐標解算,起始坐標方位角計算參照《大地測量學基礎》[5]。 xn=x0+Rcos(aoB+n·β) (14) yn=y0+Rsin(aoB+n·β) (15) 利用坐標法計算面積S公式為: (16) 利用AutoCAD內嵌的LISP人工智能編程語言進行程序設計,它的Visual LISP提供了一個完整的集成開發環境,具有編譯、調試等功能,方便地進行交互設計。VisualLISP還具有強大的圖形處理功能,二次開發程序可以便捷讀取當前AutoCAD圖形的圖元數據,以及實現圖形數據庫的修改[6]。 由于規劃設計、土地勘界和宗地權籍測繪等各種成果圖件均采用AutoCAD軟件,其成果格式為dwg、dxf等格式,故本數據處理方法的實現采用Visual LISP語言進行程序設計,程序結構流程圖如圖4所示。 圖4 程序設計流程圖 LISP程序調試完成后可以加載進AutoCAD啟動組里,于命令行鍵入“yhfd”即可調用程序執行宗地圓弧折線化及展繪坐標;也可以在Visual LISP編輯器里面進行編譯,做成擴展菜單可實現單個及批量圓弧折線化功能。該程序避免了傳統借助AutoCAD輔助分割宗地圓弧曲線的隨意性和不確定性,提升了數據質量和工作效率。 筆者從合肥市測繪設計研究院近幾年所完成的宗地權籍測繪中抽取了若干項目,均采用該模型程序進行圓曲線折線化處理制作宗地圖、計算其土地面積,與對應規劃批準的設計地塊數據對比,結果如表1所示。 折線化轉換面積驗算對比表 表1 從該表可以看出保留4位小數的面積較差中宗地含凸圓弧曲線時界址點計算面積偏小,含凹圓弧曲線時面積偏大,這說明弧線折線化后所得面積缺失或增加與前述數學推導的n·△偏差保持一致;而保留兩位小數的面積較差,各折線化地塊面積與規劃面積較差△=0.00 m2,說明折線化處理模型按界址點計算的面積其數學精度與規劃批準的面積保持一致,且兩者面積小數第3位較差不大于0.004符合不等式(13)的要求。 宗地圓弧曲線折線化是滿足《地籍測繪規范》和《土地勘測定界規程》的要求,也是國土資源部門宗地入庫、確權發證的需要。同時,城市規劃設計中大量存在的圓曲線也是空間規劃的現實需求,隨著物權法普及、兩證合一不動產權籍測繪的大規模開展,這種圓弧曲線折線化的工作必然非常多。數字測繪技術進步和社會經濟的快速發展,宗地界址點數量的控制已不再是重點,對宗地面積數學精度要求則越來越高。因此以這種分析方法為基礎,通過建立的圓曲線折線化算法模型以及LISP程序實現,我單位測量人員做到精準、高效服務合肥市國土資源規劃測繪,本宗地權籍測繪中圓曲線折線化數據處理方法展現出如下特點: (1)以圖形面積數學精度作為出發點而非規范中的面積量算誤差,建立了完整的數學誤差計算模型,系統性解決了圓弧曲線折線化問題;該數學模型還可以解決更高精度要求的面積問題,且圓弧分段均勻圖形變形小、滿足數據入庫的需要。 (2)程序操作簡單便捷,測量人員易學易用,避免了手動AutoCAD輔助弧線分段時人工干預多,分段界址點連線后還要通過折線偏移湊面積的粗略做法,該做法偶然性強使得產生界址點個數不確定,由于存在偏移使得折線段不夠精確;使用本算法和程序顯著提高作業效率、成果質量得到保證且不存在分段界址點偏移情況,降低了測量人員的工作強度,宗地圖編制更加規范高效。 (3)本圓曲線折線化處理方法在確定的數學精度下折點數是唯一確定的、分布均勻,幾乎可以做到面積無損失且界址點數最優;當前高速發展的城鎮建設、土地資源愈加昂貴,程序只要稍加擴展就可以大批量實現一個區域的圓曲線折線化,且面積偏差易于控制完全滿足土地面積量算對誤差的要求。2.4 折點坐標推算及面積量算
3 VisualLISP程序設計與工程案例驗證
3.1 程序設計流程圖
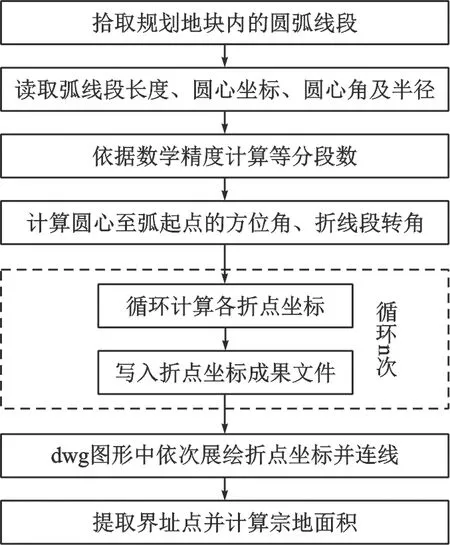
3.2 工程實例數據驗證與分析

4 結 語

