抗差Helmert估計在BDS/GPS組合定位權比分配中的應用

許 政 萬勝來 郭 強 王 闖 馮思宇

1 中航機載系統共性技術有限公司, 江蘇省揚州市沙灣中路9號, 225000

隨著全球導航衛星系統(global navigation satellite system，GNSS)的快速發展，多系統組合定位成為必然趨勢。相比于其他衛星導航系統，BDS與GPS有更好的兼容性[1-3]，且雙系統組合可顯著增加可見衛星數量，改善衛星的幾何分布，從而提高定位精度及可靠性。

但由于實際解算中觀測值來自于2個不同的系統，其觀測噪聲與隨機誤差各不相同，傳統等權模型將雙系統觀測值籠統地歸為一類，反而會降低組合定位的精度[4]。因此，獲取能表征觀測值隨機噪聲水平的方差-協方差陣[5]，構建精確的隨機模型，進而準確地給出兩類觀測值的權比，實現組合定位精度的提升，是近年來國內外學者廣泛關注的熱點問題[6-9]。

為解決這一問題，本文提出一種利用抗差Helmert方差分量估計定權的BDS/GPS組合定位算法。首先，構建Helmert方差分量估計組合定位模型；然后，引入基于IGGⅢ方案的等價權函數，改進權函數調節因子，解決由粗差導致的方差分量估計模型失真的問題；最后，通過BDS/GPS雙系統實測數據對所提算法的有效性和優越性進行仿真驗證。

1 抗差Helmert方差分量估計算法設計

1.1 Helmert方差分量估計

假定BDS和GPS觀測陣LB和LG相互獨立，由參數平差模型構成的誤差方程為：

(1)

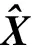
根據最小二乘法代價函數最小理論，誤差方程為：

(2)

根據二次型期望公式推導出嚴密Helmert方差分量估計為：

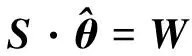
(3)

式中，

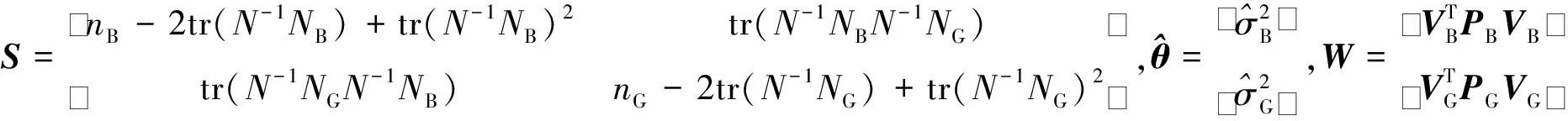
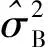
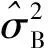
(4)

1.2 基于IGGⅢ方案的抗差估計權函數設計

Helmert方差分量估計不具備抗差性，當系統觀測值中存在粗差時，粗差產生的影響可能會轉移到隨機模型中，造成模型失真。引入抗差估計權函數，生成等價權矩陣對可疑數據進行降權處理，削減粗差的影響，提升系統的抗干擾能力和可靠性。

按照抗差估計理論，建立目標函數：

(5)

式中，i表示觀測類型，j表示某類觀測值數量，ρ(·)為連續凸函數，(Pj)i為權函數，(Vj)i為殘差函數。

基于等價權原理，可得抗差估計：

(6)

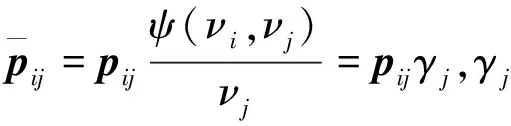
通過選取合適的權函數，確定等價權矩陣，可實現抗差估計，因此權函數的選取至關重要。本文選用基于IGGⅢ方案的抗差估計權函數：

(7)

式中，常數k1一般取值為1.5～2.0，常數k2一般取值為3.0～8.5，σ為ν的中誤差，σ=median(|νj|)/0.674 5。

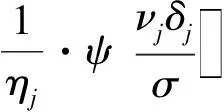
(8)

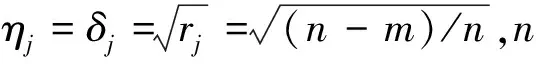
(9)

1.3 抗差Helmert方差分量估計算法流程

1) 將BDS與GPS兩系統之間的初始權比設為PB=PG=1，同一系統內部根據高度角模型進行定權：

Pij=sin(Ej)

式中，Pij為權值，Ej為第j顆衛星的高度角。

2) 按式(1)進行預平差計算，獲取BDS與GPS系統的觀測值殘差信息VB和VG；

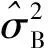
4) 按式(4)重新調整兩系統間的權陣；

5) 根據抗差估計理論，按式(9)計算自適應抗差因子，降低含粗差觀測值的權重；

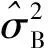
2 實驗驗證

使用接收機實際采集到的BDS/GPS組合系統觀測數據與導航電文，對本文所提抗差組合定位算法(robust Helmert算法，簡稱RH算法)的性能進行仿真驗證。接收機的真實空間直角坐標為[-2 364 332.717 2 m,4 870 286.103 8 m,-3 360 810.227 0 m]，采樣周期為30 s，采樣時間為24 h，共計2 880個歷元，抗差估計權函數參數設為k1=1.5、k2=3.0。

為驗證本文算法的正確性和有效性，選用基于高度角模型的最小二乘least squares組合定位算法(LS算法)和經典Helmert方差分量估計組合定位算法進行對比實驗。分別利用3種算法對實際采集到的BDS/GPS組合系統觀測數據進行定位解算，通過表征輸出定位結果聚合度的極差和均方根誤差(RMS)指標來評價各算法的定位性能。

無粗差情況下的仿真結果如圖1和表1所示，可以看出，Helmert算法和RH算法在觀測歷元內的誤差曲線穩定，未出現大幅波動，而LS算法的誤差曲線波動略大，甚至在個別時刻出現了較大跳躍。

圖1 未添加粗差的定位誤差序列Fig.1 Positioning error diagram without gross error injection

表1 未添加粗差的定位結果對比

從表1定位結果可以看出，由Helmert算法和RH算法得到的E、N、U方向上的定位極差和RMS結果均優于LS算法。

Helmert算法和RH算法在2 880個歷元內GPS與BDS系統間權比的均值分別為3.86和3.41，雙系統間重新定權后，性能優于僅通過高度角定權的LS算法。

為驗證本文RH算法的組合定位性能，人為給GPS系統內一顆隨機衛星的偽距觀測值添加75 m的粗差，結果如圖2和表2所示。可以看出，LS算法受粗差影響，定位誤差波動較大，與表1相比定位性能急劇下降；Helmert算法在2 880個歷元內GPS與BDS系統間權比的均值為0.02，雖通過實時調整GPS系統權值盡可能降低了粗差帶來的影響，但從E、N、U方向上部分歷元的誤差曲線出現階躍可以看出，影響未被完全消除，定位性能有所下降；RH算法在2 880個歷元內GPS與BDS系統間權比的均值為4.45，與未添加粗差時的權比接近，誤差曲線穩定，未出現大幅波動。表2中的定位性能指標數據與表1相似，可見具有抗差模型的RH算法不僅可合理地定權，同時能夠較好地抑制粗差帶來的影響。

圖2 單系統添加粗差的定位誤差序列Fig.2 Single system positioning error diagram with gross error injection

表2 單系統添加粗差的定位結果對比

為進一步驗證RH算法的組合定位性能，在每一歷元分別給GPS和BDS系統內一顆隨機衛星的偽距觀測值添加75 m的粗差，結果如圖3和表3所示。可以看出，因雙系統內增加了一顆含偽距粗差的衛星，LS算法在E、N、U方向上的極差和RMS受到影響，誤差進一步累加，證明僅通過高度角定權的LS算法完全無法抵御粗差；Helmert算法在2 880個歷元內GPS與BDS系統間權比的均值為6.25，雙系統均出現含粗差的衛星，導致算法無法通過實時調整權值降低粗差帶來的影響，且從E、N、U方向上的誤差曲線及定位性能指標數據可以看出，整體性能降幅較大，部分歷元定位結果偏差甚至大于高度角定權的LS算法，可見粗差已經導致Helmert算法模型收斂失真；RH算法在2 880個歷元內GPS與BDS系統間權比的均值為5.24，通過抗差模型消減含粗差衛星的權值，降低粗差的影響，使得系統間權比與前2次仿真結果接近且較為穩定。表3中定位性能指標數據與表2相比略有下降，從圖3可以看出，E、N、U方向上的誤差曲線在個別歷元出現波動，對數據進行分析發現，添加粗差后部分正常衛星偽距觀測值被“污染”，殘差增幅達到抗差模型的臨界狀態，使得抗差效果有所降低。總體來說，RH算法能夠較好地抑制粗差帶來的影響，性能符合預期。

圖3 雙系統添加粗差的定位誤差序列Fig.3 Dual system positioning error diagram with gross error injection

表3 雙系統添加粗差的定位結果對比

3 結 語

本文針對組合定位中系統間權比分配的問題，提出一種抗差Helmert方差分量估計組合定位方法，引入并優化基于IGGⅢ方案的抗差估計模型，通過自適應抗差因子動態消減可疑觀測，抵御粗差，改善經典Helmert算法估計模型收斂失真的問題。通過仿真對比實驗證明，當BDS與GPS兩系統的偽距觀測值均存在粗差時，本文算法可有效抑制組合系統粗差觀測值的影響，合理確定兩類觀測值的權比，提高組合定位的精度與可靠性。