一種基于BDS-3四頻數據的周跳探測與修復方法

呂 震 王振杰 聶志喜 徐曉飛 張遠帆

1 中國石油大學(華東)海洋與空間信息學院，青島市長江西路66號, 266580

載波相位觀測是GNSS高精度定位及應用的關鍵[1]。由于接收機自身原因或GNSS信號受物理遮蔽等因素的影響，載波相位觀測可能發生周跳，因此當載波相位觀測量參與GNSS高精度定位及相關應用時，需要進行有效的周跳探測和修復[2]。目前常用的GNSS雙頻觀測值周跳探測方法有TurboEdit方法、卡爾曼濾波法、多普勒積分法等，其中TurboEdit方法具有探測精度高、程序容易實現等優點，應用最為廣泛[3]。隨著三頻GNSS的發展，相關學者針對三頻周跳探測與修復的特性及方法展開了大量研究[4-6]。

如今中國北斗三號全球衛星導航系統BDS-3和歐盟Galileo系統已經可以播發4個頻率的信號[7-8]，四頻周跳處理方法相較于GNSS雙頻和三頻具有更廣闊的應用前景[9]，而目前針對GNSS四頻周跳探測與修復特性及方法的研究較少。限于篇幅，本文僅利用BDS-3提供的四頻信號研究周跳探測與修復的新方法，選用B1C、B1I、B2a、B3I四個頻率信號，根據電離層延遲最小和組合觀測值噪聲最小原則對組合系數進行優選，聯合四頻無幾何相位組合和四頻無幾何無電離層組合兩種方法進行周跳探測，然后基于最小二乘法估計周跳浮點解，最后利用MGEX提供的BDS-3四頻數據驗證本文算法的有效性和可靠性。

1 四頻組合觀測值系數選擇

1.1 四頻無幾何相位組合觀測值特性分析

GNSS原始偽距和載波相位觀測值的觀測方程可以寫為[9]：

Pi=ρ+c(dtr-dts)+T+ηiI1+εPi

(1)

λiφi=ρ+c(dtr-dts)+T-ηiI1+λiNi+λiεφi

(2)

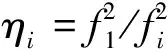
對式(2)進行組合[10]，可以得到四頻無幾何GF相位組合：

φGF=αλ1φ1+βλ2φ2+γλ3φ3+δλ4φ4=

-ηGFI1+NGF+εGF

(3)

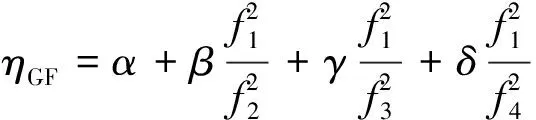
為滿足無幾何條件[10]，提高周跳探測的靈敏度，令

(4)

對相鄰歷元的GF組合觀測值進行歷間差分可得：

ΔNGF=NGF(k)-NGF(k-1)=

ΔφGF-ηGFΔI1+ΔεGF

(5)

式中，ΔφGF為相鄰歷元差分后的GF相位組合，ΔNGF為GF相位組合周跳探測量，k和k-1為當前歷元和前一歷元。

由式(5)可知，ΔNGF會受到ηGFΔI1和ΔεGF的影響，因此在選擇組合系數時應盡量選擇ηGFΔI1和ΔεGF較小的組合。在高采樣率條件下，ΔI1的值極小，當ηGF也極小時，ηGFΔI1可忽略不計。根據誤差傳播定律，ΔNGF的標準差可表示為式(6)，此處σφ取0.01周：

σΔNGF=

(6)

以4倍周跳探測量標準差(對應正態分布假設下99.9%的置信水平)作為周跳探測閾值，GF相位組合探測出周跳的條件為：

|ΔNGF|≥4σΔNGF

(7)

上述公式中的4個頻點分別對應BDS-3的B1C(1 575.420 mHz)、B1I(1 561.098 mHz)、B2a(1 176.450 mHz)和B3I(1 268.520 mHz)。在[-10,10]范圍內BDS-3較優的GF相位組合系數及10周以內不敏感周跳個數如表1所示，由表可見，對于任一GF相位組合均存在不敏感周跳，但不同組合的不敏感周跳是不同的。為此，從表1中選取3個GF相位組合同時進行周跳探測，以減少不敏感周跳的組合數并提高周跳探測的靈敏度。以式(4)作為組合系數選擇條件，同時保證聯合使用3個GF相位組合時不存在10周以內的不敏感周跳。通過篩選，BDS-3組合[1,-1,0,0]、[0,1,0,-1]和[0,0,-1,1]滿足條件，因此本文選擇上述3個GF相位組合作為設定條件下的最優組合。由于四頻GF相位組合中的任意4個都是線性相關的，因此無論使用多少個GF相位組合，總存在不敏感周跳。為解決這一問題，本文選擇四頻無幾何無電離層GIF組合聯合四頻GF相位組合進行周跳探測。

1.2 四頻無幾何無電離層組合系數選擇

根據式(1)和式(2)可知，四頻GIF組合可以表示為：

φGIF=iφ1+jφ2+kφ3+lφ4-

iN1+jN2+kN3+lN4+εGIF

(8)

式中，i、j、k、l為GIF組合載波相位組合觀測值系數，a、b、c、d為GIF組合偽距組合觀測值系數，λGIF=c/(if1+jf2+kf3+lf4)為組合波長，iN1+jN2+kN3+lN4=NGIF為組合模糊度，組合觀測噪聲為εGIF=iεφ1+jεφ2+kεφ3+lεφ4-(aεp1+bεp2+cεp3+dεp4)/λGIF。

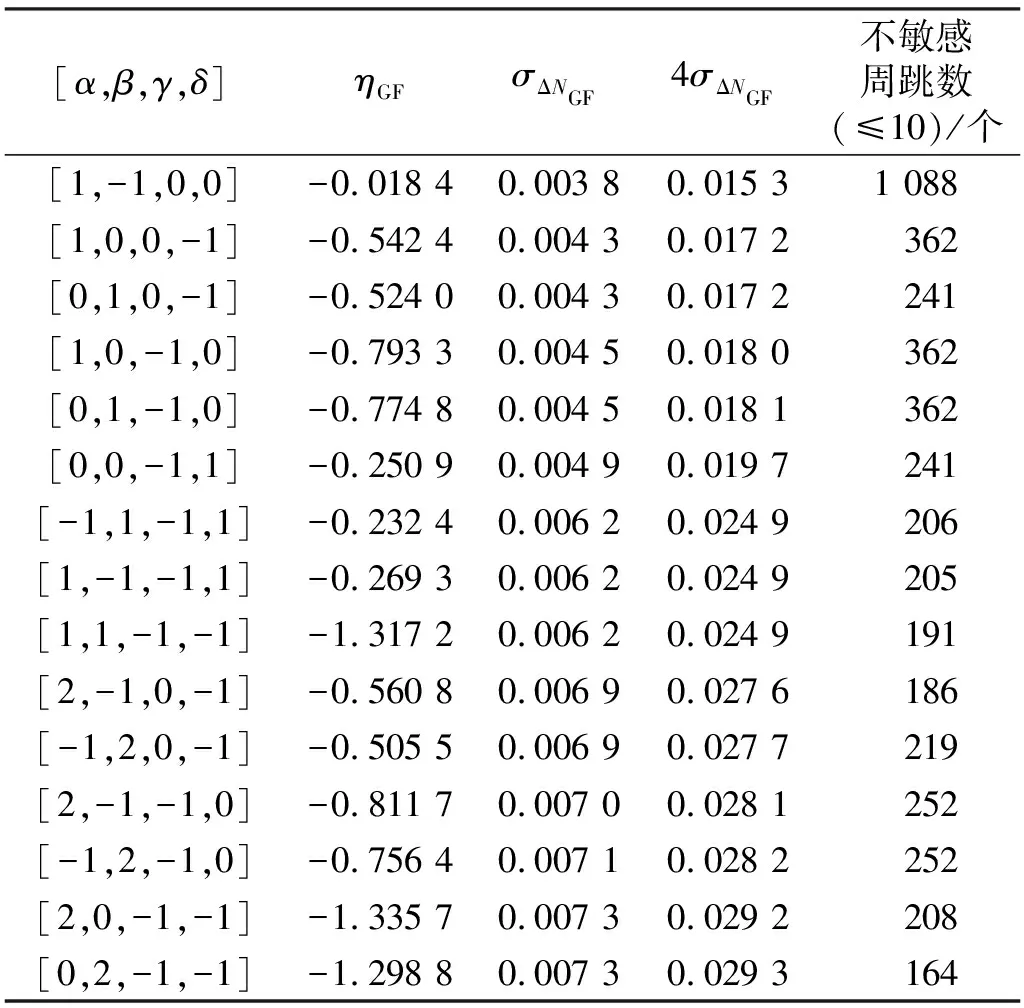
表1 BDS-3四頻無幾何相位組合及不敏感周跳個數

為消除幾何誤差項和電離層誤差一階項，盡可能降低偽距噪聲的影響[4]，需滿足：

(9)

當發生周跳時，通過歷元間差分可構造周跳探測方程：

ΔNGIF=NGIF(k)-NGIF(k-1)=ΔφGIF+ΔεGIF

(10)

式中，ΔφGIF為相鄰歷元差分后的GIF組合，ΔNGIF為GIF組合周跳探測量，k和k-1為當前歷元和前一歷元。

根據誤差傳播定律，ΔNGIF的標準差可表示為式(11)，此處σφ取0.01周，σP取0.1 m：

σΔNGIF=

(11)

同樣以4倍周跳探測量標準差作為周跳探測閾值，GIF組合探測出周跳的條件為：

|ΔNGIF|≥4σΔNGIF

(12)

在GIF組合系數篩選過程中，首先要確定載波相位組合系數[i,j,k,l]，然后在滿足式(9)前兩式的條件下在[-1,1]范圍內對偽距組合系數a、b、c、d進行搜索，最后將滿足a2+b2+c2+d2=min的偽距組合系數a、b、c、d及對應的載波相位組合系數[i,j,k,l]作為該設定條件下的最優GIF組合。通過篩選，BDS-3四頻較優的GIF組合如表2所示，由表可知，觀測噪聲σΔNGIF越小，周跳探測靈敏度越高，因此為了減小σΔNGIF，應選擇λGIF更長的超寬巷或寬巷組合。以4σΔNGIF作為探測閾值時，周跳探測組合均可實現對1周小周跳的探測，為了表達簡便，以載波相位組合系數[i,j,k,l]表示GIF組合。當BDS-3組合[1,-1,0,0]具有較長的波長時，觀測噪聲達到最小，且周跳探測閾值均不超過0.1周，因此選擇組合[1,-1,0,0]作為BDS-3四頻GIF組合的周跳探測組合。針對3個GF相位組合中存在不敏感周跳的問題，采用一個GIF組合構成4個線性無關的組合，可以保證無公共不敏感周跳組合，從而實現對各類周跳的探測。

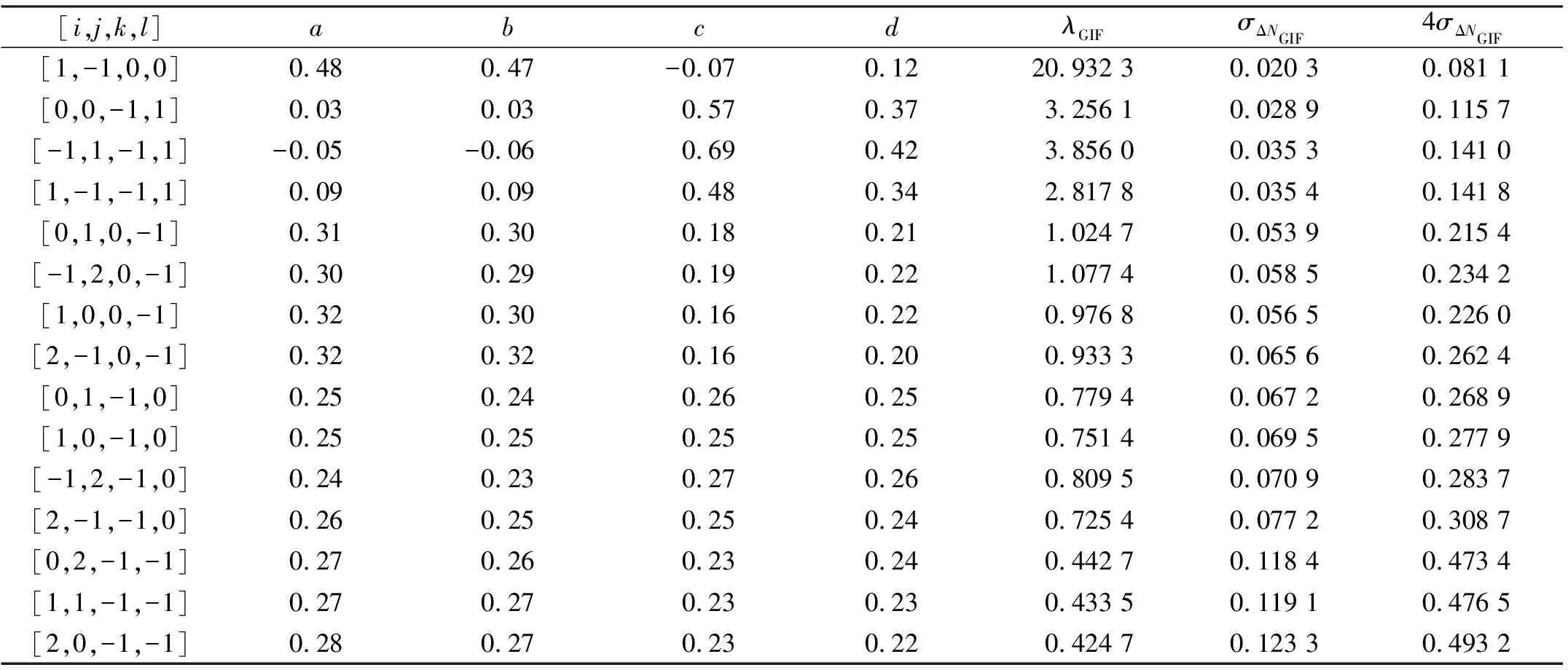
表2 BDS-3四頻無幾何無電離層組合

2 四頻數據的周跳探測與修復

本文采用3個四頻GF相位組合和1個四頻GIF組合構造4個線性無關的周跳探測組合，以4倍周跳探測量標準差作為周跳探測閾值。當滿足周跳探測量大于探測閾值時，表明相應歷元發生了周跳。通過對GF相位組合系數和GIF組合系數進行優選，得到3個GF相位組合和1個GIF組合，其中BDS-3組合系數對應[1,-1,0,0]、[0,1,0,-1]、[0,0,-1,1]和[1,-1,0,0]，周跳探測閾值分別為0.015 3、0.017 2、0.019 7和0.081 1。

當載波相位觀測值中的周跳被成功探測后，需要對周跳進行修復。在每個歷元下，通過聯立3個GF相位組合觀測值和1個GIF組合觀測值得到組合觀測值L，這里L表示為[LGF1,LGF2,LGF3,LGIF]T，其中LGF1、LGF2、LGF3為3個不同的GF相位組合觀測值，LGIF為GIF組合觀測值；然后在相鄰歷元間對L進行求差，可得歷元間差分后的組合觀測值ΔL。當ΔL探測出周跳后，根據式(13)即可得到單個頻點上的待估周跳值ΔX：

AΔX+ε=ΔL

(13)

式中，ε為觀測噪聲，ΔX=[ΔN1,ΔN2,ΔN3,ΔN4]T為4個不同頻點上的待估周跳浮點解，A為其系數矩陣，此處表示為：

(14)

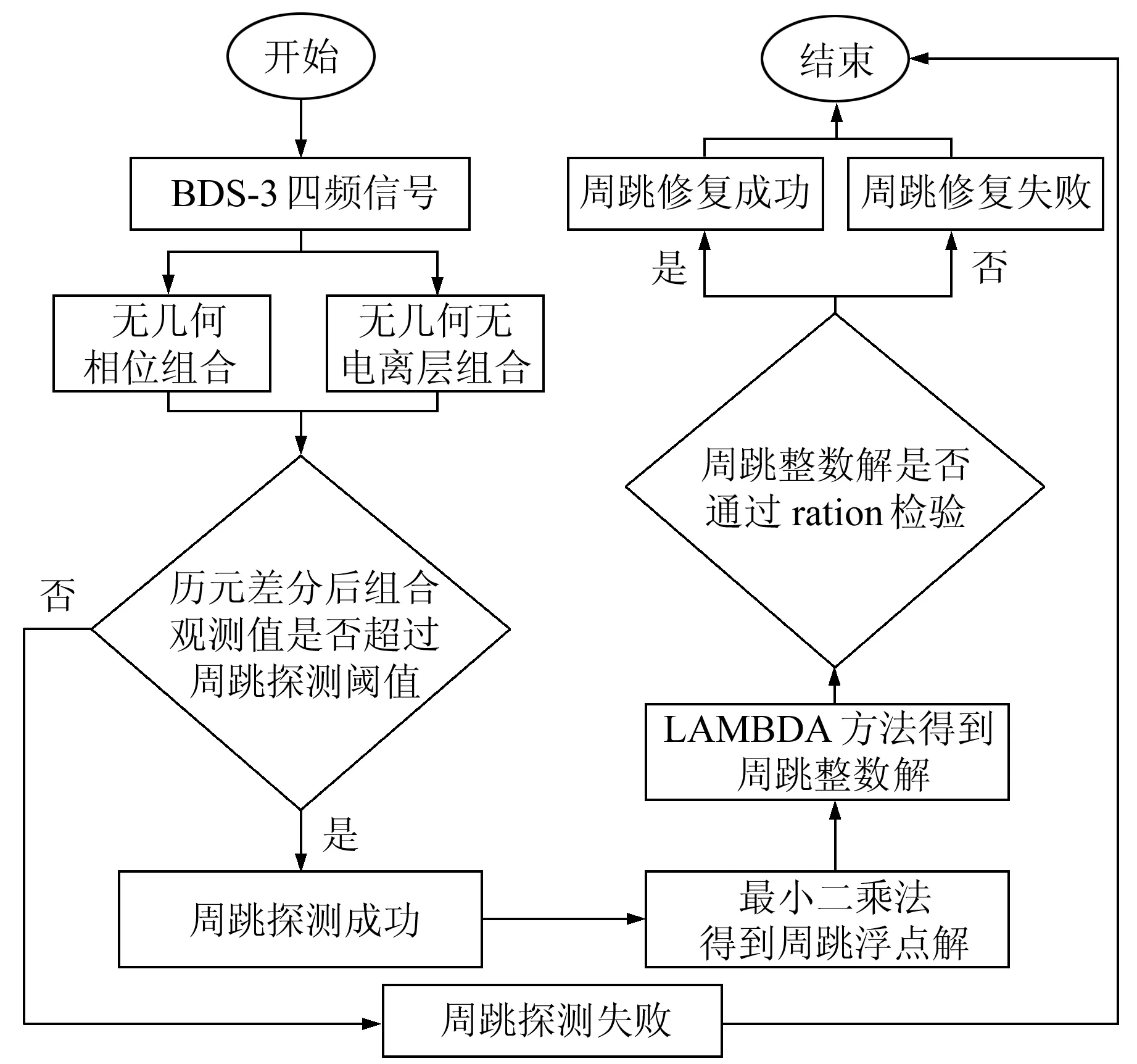
圖1 BDS-3四頻周跳探測與修復算法流程Fig.1 Procedure of quad-frequency cycle-slip detection and repair algorithm for BDS-3

3 實驗分析

選取MGEX提供的WUH2測站(30.53°N，114.36°E)2020-10-26的觀測數據，采樣間隔為1 s，衛星截止高度角為10°。其中，BDS-3系統選擇C39和C40兩顆衛星，每顆衛星選擇連續500個沒有周跳和粗差的歷元作為本次實驗的觀測時間序列。

由圖2可見，3個GF載波相位組合探測量的波動均保持在[-0.02,0.02]范圍內，而GIF組合周跳探測量在[-0.1,0.1]范圍內。由此可知，相較于GIF組合，GF相位組合的周跳探測能力更高，這是因為GF相位組合比GIF組合受到的噪聲影響更小。

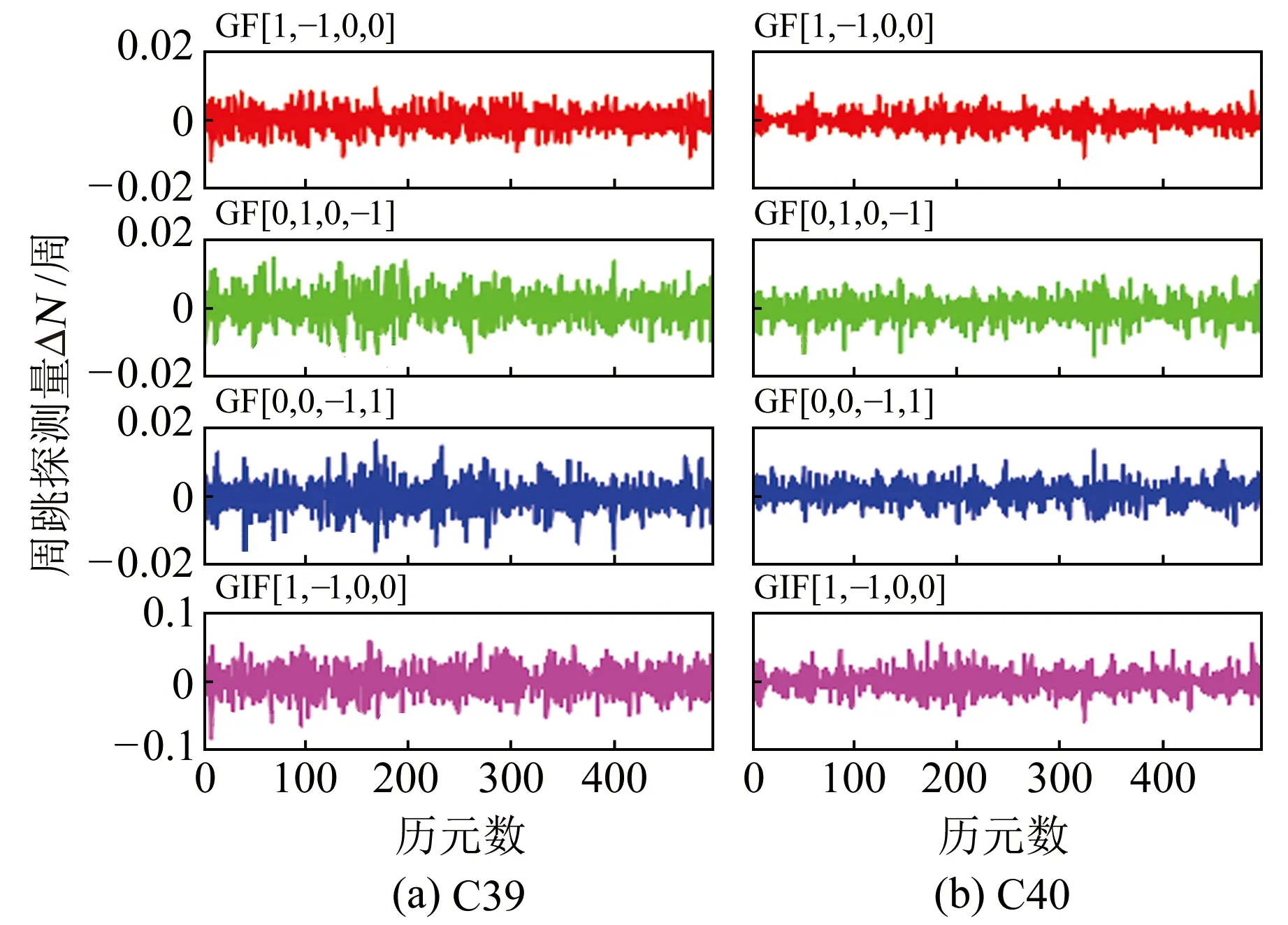
圖2 BDS-3無周跳組合探測值Fig.2 Combination detection values without cycle-slip for BDS-3

由于原始測站非差觀測值中無周跳，因此本文在不同歷元時刻加入一般周跳和特殊周跳(一般周跳指4個組合均可以探測出的1～10周的周跳，特殊周跳指單個頻率上發生1～2周的小周跳或者在不同頻率發生相同跳變的小周跳)，以驗證本文所選線性組合的周跳探測能力及修復效果。

3.1 一般周跳的探測與修復

分別在BDS-3 C39和C40衛星每隔100個歷元加入不同的10周以內一般小周跳(3,1,2,1)、(6,7,4,3)、(1,4,3,2)、(5,7,4,7)，探測結果如圖3所示。由圖可見，4個組合均可同時檢測到一般周跳，BDS-3具體周跳探測與修復結果列于表3。由表可知，所有一般周跳的ratio值均大于閾值，同時利用LAMBDA算法得到的周跳計算值與周跳模擬值均保持一致，從而驗證了采用LAMBDA算法對一般周跳進行修復的正確性。

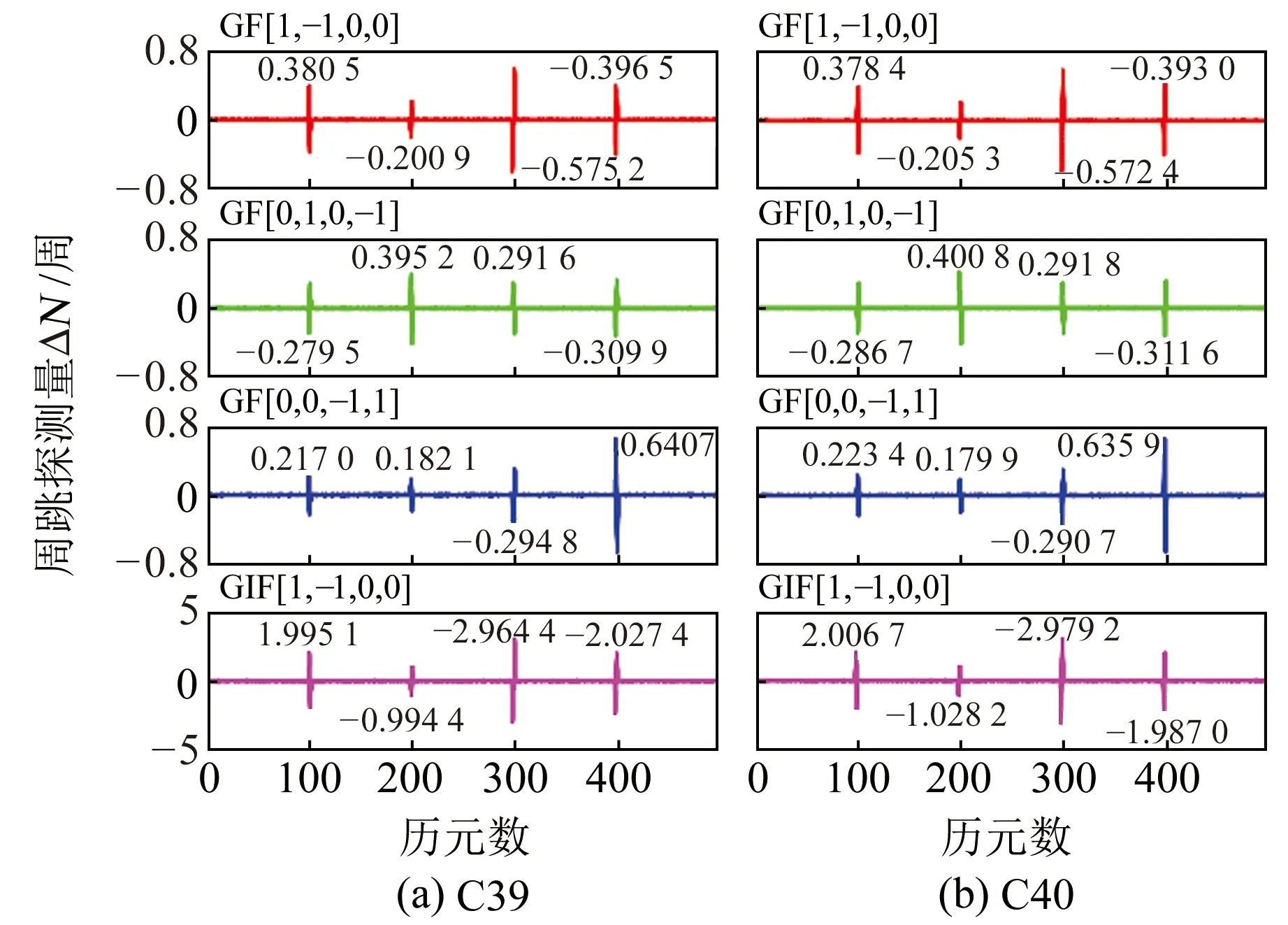
圖3 BDS-3一般周跳組合探測值Fig.3 Normal cycle-slip combination detection values for BDS-3

表3 BDS-3一般周跳的周跳探測與修復結果

3.2 特殊周跳的探測與修復

為進一步驗證本文方法的周跳探測與修復效果，分別在BDS-3 C39和C40衛星不同歷元時刻加入特殊周跳，探測結果如圖4所示。

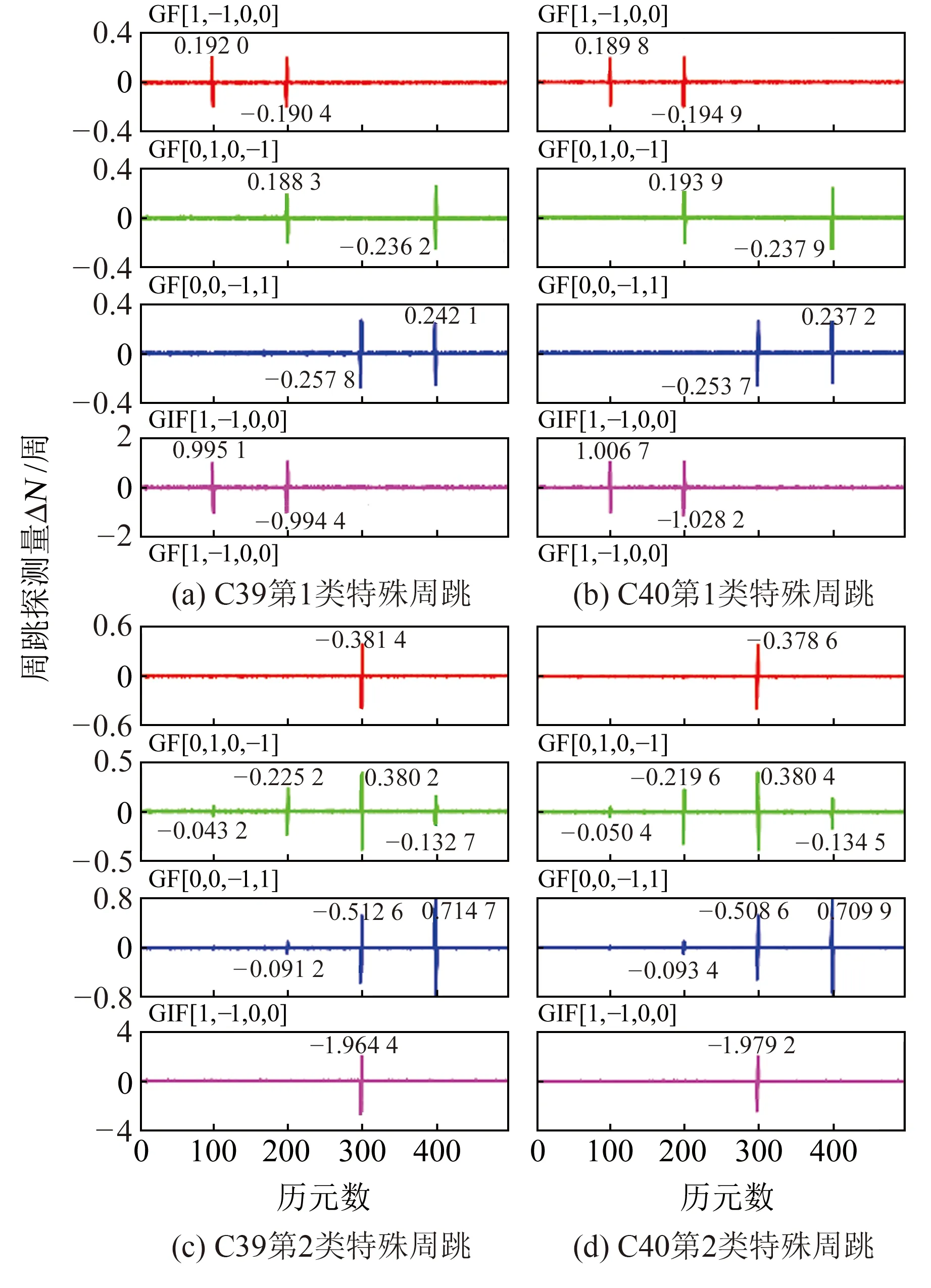
圖4 BDS-3特殊周跳組合探測值Fig.4 Particular cycle-slip combination detection values for BDS-3

首先考慮當4個頻率信號中某一單獨頻點發生周跳的情況，分別在第100、200、300、400歷元中加入周跳(1,0,0,0)、(0,1,0,0)、(0,0,1,0)、(0,0,0,1)。由圖4(a)和4(b)可見，GF相位組合[1,-1,0,0]和GIF組合均可探測出周跳(1,0,0,0)；對于周跳(0,1,0,0)，僅有GF相位組合[0,0,1,-1]對其不敏感；采用GF相位組合[0,0,-1,1]可探測出周跳(0,0,1,0)和(0,0,0,1)。考慮其他特殊的不敏感周跳，在第100和200歷元加入4個頻點發生相同周跳的周跳組合(1,1,1,1)和(5,5,5,5)，在第300歷元加入頻點2和頻點3發生相同周跳的周跳組合(0,2,2,0)，在第400歷元加入頻點1、頻點3、頻點4同時發生相同周跳的周跳組合(3,3,0,3)。由圖4(c)和4(d)可見，對于周跳組合(1,1,1,1)，C39和C40衛星的GF相位組合[0,1,0,-1]的探測量均超過探測閾值；對于周跳(5,5,5,5)、(0,2,2,0)和(3,3,0,3)，C39和C40衛星的GF相位組合[0,1,0,-1]和[0,0,-1,1]均可將其探測出。

通過分析可知，特殊的不敏感周跳可能對部分探測組合不敏感，但4個組合聯合后均能很好地探測出周跳，極大地減少了探測盲區。BDS-3四個組合特殊周跳的周跳探測及修復具體信息列于表4，由表可知，所有特殊周跳的ratio值均大于閾值，且計算值均與模擬值相同，表明采用LAMBDA方法同樣可以對特殊周跳進行準確修復。

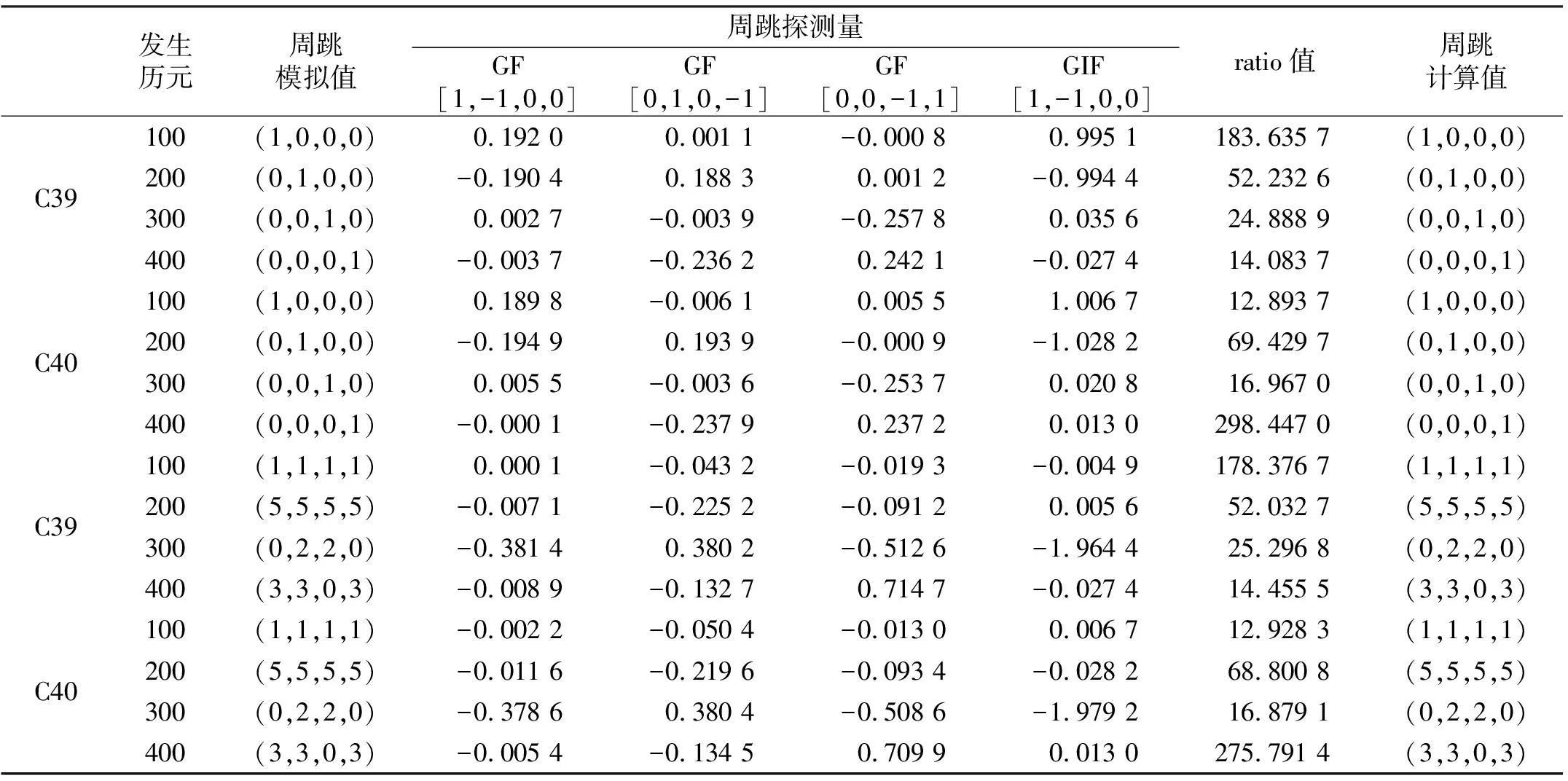
表4 BDS-3特殊周跳的周跳探測與修復結果

4 結 語

本文對BDS-3四頻數據的周跳探測與修復方法進行研究，首先基于無幾何條件下的觀測噪聲最小準則優選出3個GF相位組合，再基于無幾何無電離層條件下的觀測噪聲最小準則優選出1個GIF組合，并聯合4個組合觀測值進行周跳探測。在探測出周跳后，將4個周跳探測組合進行方程組聯立，采用最小二乘法確定周跳浮點解，基于LAMBDA降相關搜索法獲得周跳整數解，并采用ratio檢驗進一步對周跳整數解進行驗證。最后采用MGEX提供的BDS-3四頻觀測數據進行實驗驗證，結果表明，本文提出的方法可以實現對單站非差觀測值中各類周跳的準確探測及快速高效修復。值得說明的是，本文提出的方法同樣可以用于Galileo四頻數據的周跳探測與修復，限于篇幅，本文不進行具體介紹。