一個捕食者染病、食餌具有階段結構的生態-流行病模型的穩定性
張 梅, 王玲書, 賈美枝
(河北經貿大學數學與統計學學院,石家莊 050061)
0 引言
近年來,許多學者研究了傳染病對種群模型的影響,即生態-流行病模型的穩定性[1–11]。由于傳染病可以在種群內部或種群之間相互傳播,從而使得這些模型有著豐富的研究內容。文獻[7]研究了下列生態-流行病模型
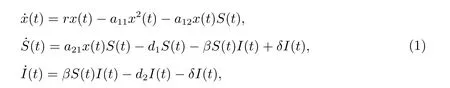
其中x(t)、S(t)和I(t)分別表示食餌、易感捕食者和染病捕食者種群在時刻t的密度。參數r> 0 表示食餌種群的內稟增長率;a11> 0 為食餌種群的種內競爭率;d1> 0 和d2>0 分別表示易感捕食者和染病捕食者的死亡率;a12>0 表示捕食者捕食食餌的捕獲率,捕食者的生育轉化率為a21/a12;β>0 為疾病的傳染率;染病捕食者的治愈率為δ>0。
由于時滯微分方程相對于不含時滯的傳統的常微分方程能夠更準確地描述種群的變化規律。為此,在生態系統研究中,采用具有時間滯后的微分方程來建立數學模型變得越來越普遍[9–13]。文獻[11]在模型(1)的基礎上考慮了下列具有時滯的微分系統
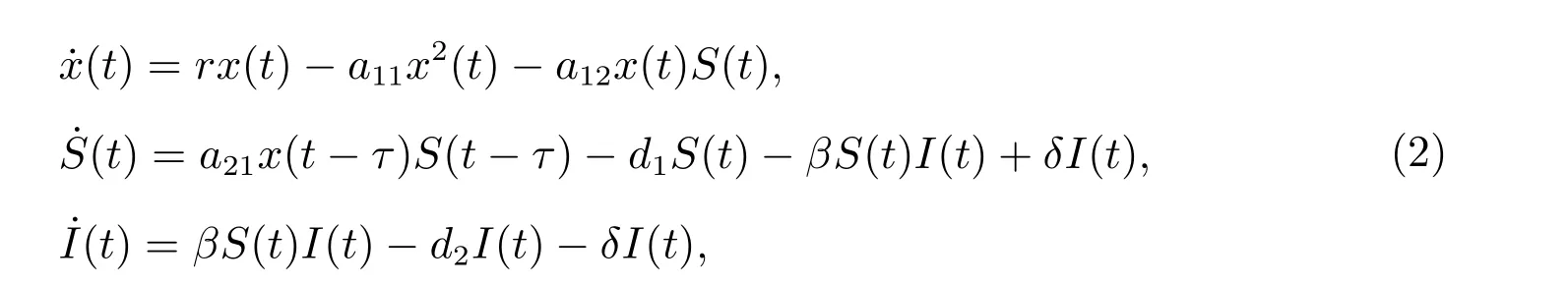
其中τ ≥0 表示捕食者種群的妊娠期所引起的時滯。文獻[11]討論了模型(2)的非負平衡點的穩定性,得到了正平衡點處存在Hopf 分支的充分條件。
本文在模型(1)和(2)的基礎上,研究一個食餌具有階段結構,捕食者具有Holling-II 型功能性反應的捕食者—食餌模型。為此,考慮下列生態—流行病模型
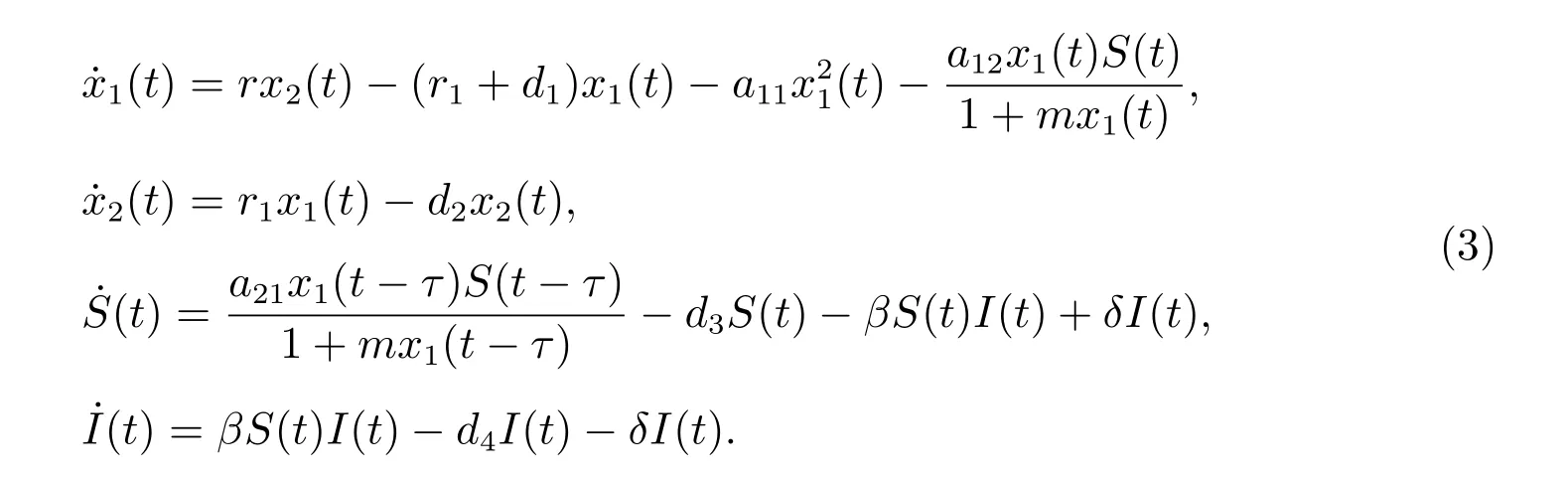
在模型(3)中,食餌種群分為幼年和成年兩個階段,它們在時刻t的密度為x1(t)和x2(t)。參數r1> 0 表示幼年食餌向成年食餌的轉化率,di> 0(i= 1,2,3,4)分別表示幼年食餌、成年食餌、易感捕食者和染病捕食者的死亡率;p(x) =x/(1+mx)表示捕食者對食餌的Holling-II 型功能性反應函數;模型(3)假設易感捕食者僅捕食幼年食餌。
模型(3)滿足的初始條件為
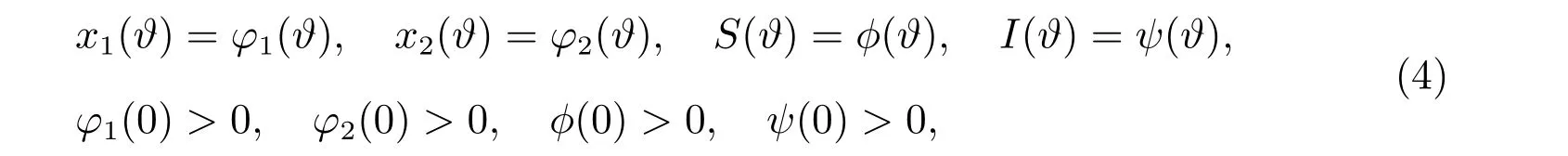
其中φ1(?)和?(?)為[?τ,0]上的非負連續函數。由文獻[14]可知,模型(3)和(4)存在唯一的正解。
1 平衡點的局部穩定性
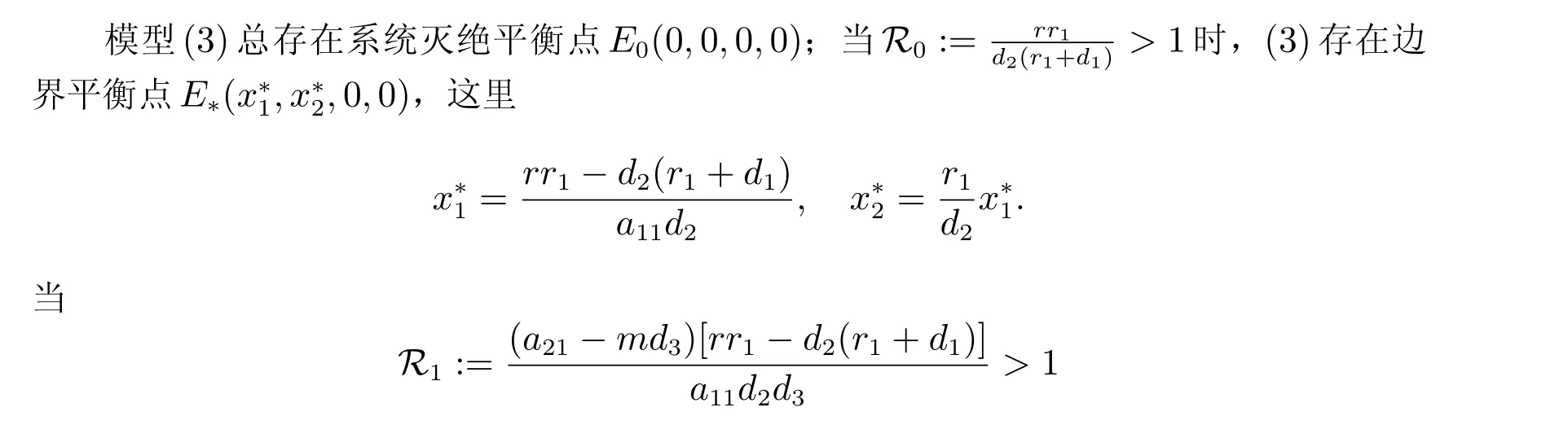
時,模型(3)存在無病平衡點E′(x′1,x′2,S′,0),這里

1.1 正平衡點的局部穩定性及其Hopf 分支
假設R2>1 成立,則模型(3)在點E+處的特征方程有下面形式
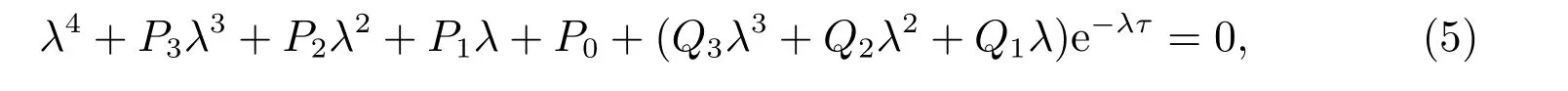
這里
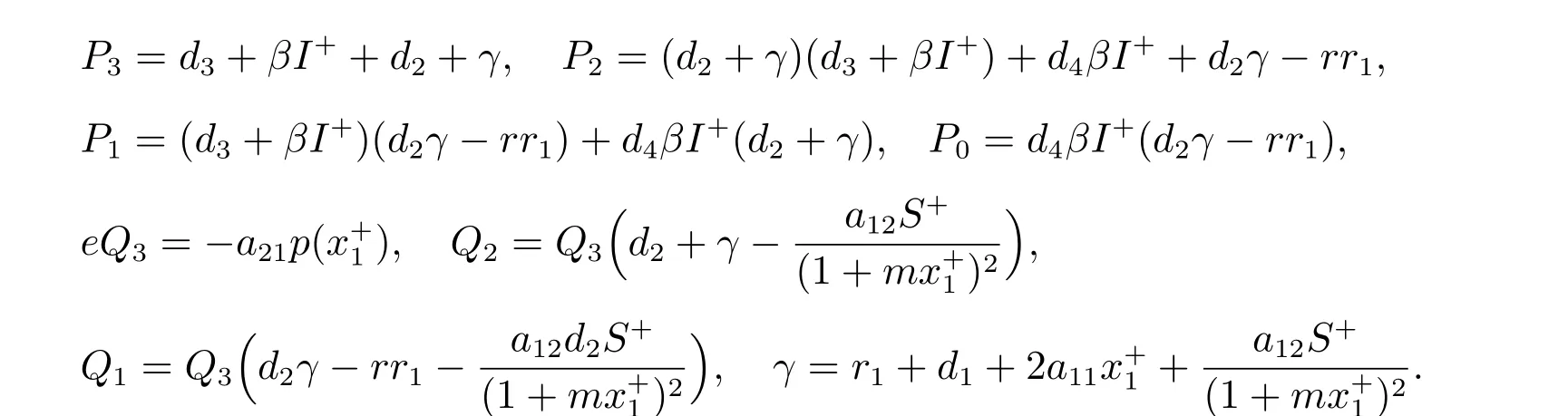
如果τ=0,由(5)式可得

假設d2γ>rr1,則下面不等式成立+
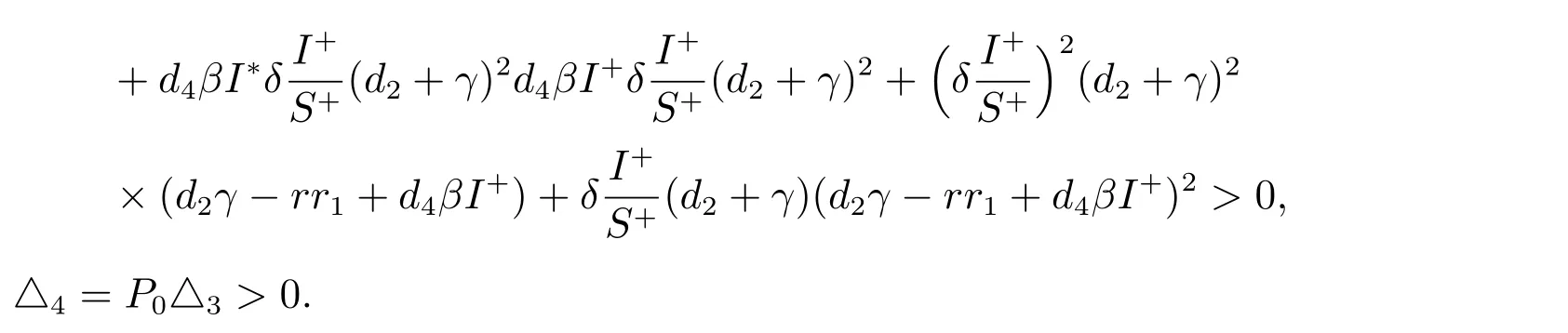
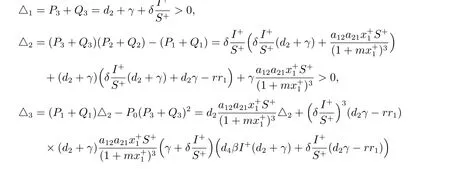
由Routh-Hurwitz 準則[15],此時,E+局部漸近穩定。
如果λ=±iν(ν>0)是方程(5)的根,將λ=iν代入(5),有下面方程
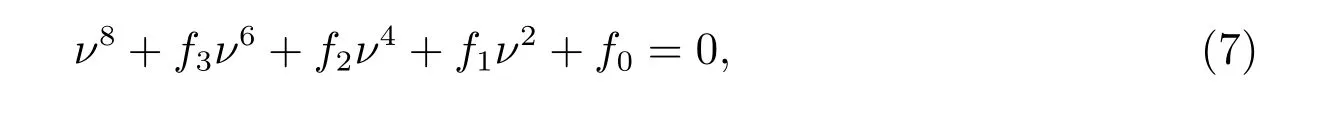
其中
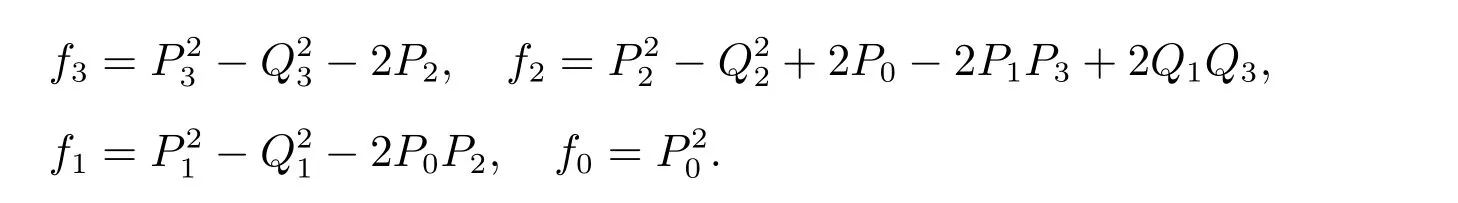
設y=ν2,由方程(7)可得

1.2 邊界平衡點的局部穩定性
由特征值理論易證,當R0< 1 時,系統滅絕平衡點E0局部漸近穩定;當R0>1 時,E0不穩定。假設R0>1 成立,直接計算可得,模型(3)在E?處有下面特征方程

顯然,方程(10)有一個實根λ=βS′?d4?δ。若R2<1,則λ<0。現在考慮下面方程

如果τ=0,則有

由(12)式可得
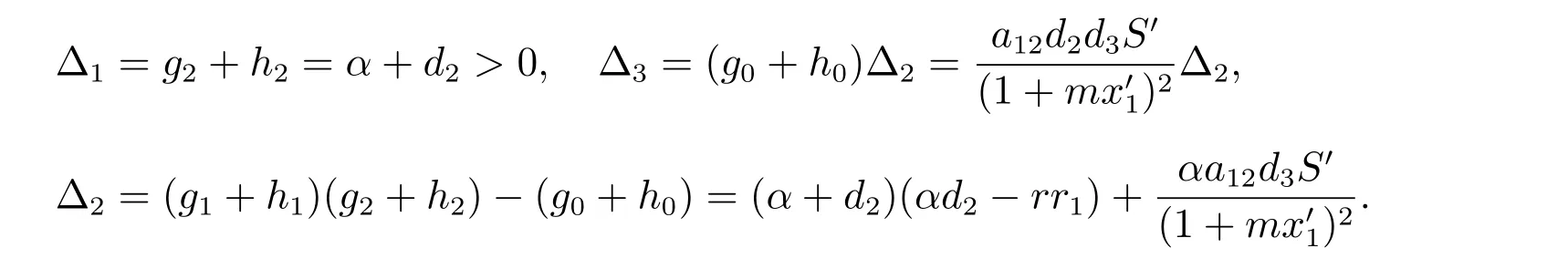
若αd2>rr1,則有?2>0 且?3>0。類似于定理1 的討論,可知E′局部漸近穩定。
綜合上面的分析,可以得到下面定理。
定理2 對于模型(3),有:
(i) 當R0<1 時,E0局部漸近穩定;當R0>1 時,E0不穩定;
(ii) 假設R0>1 成立,則當R1<1 時,E?局部漸近穩定;當R1>1 時,E?不穩定;
(iii) 假設R1> 1 且αd2>rr1成立,則當R2< 1 時,E′局部漸近穩定,當R2>1 時,E′不穩定。
2 平衡點的全局穩定性
本節我們討論模型(3)的永久持續生存和滅絕問題,即模型(3)的各個平衡點的全局穩定性。
2.1 正平衡點的全局穩定性
引理1 對充分大的t,存在常數C>0 和C1>0,使得
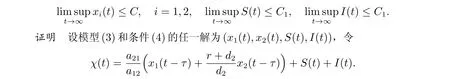
求χ(t)的導數,可得

其中C1同引理1。
證明 對任意的ε>0,由引理1 可知,存在t0>0,使得t>t0時,S(t) 由此不等式組可知 引理2 得證。 定理3 設模型(3)和條件(4)的任一解為(x1(t),x2(t),S(t),I(t)),若R2>1,且 證明 易證,模型(3)具有下面形式 令 由(14)式可知 定理4 設模型(3)和條件(4)的任一解為(x1(t),x2(t),S(t),I(t)),若R0< 1,則E0全局漸近穩定,即系統將滅絕。 證明 由定理2 可得,當R0< 1 時,E0局部漸近穩定,故這里僅需證明E0是全局吸引的。定義 在A0上考慮模型(3)的解可得 因此x2(t) = 0,即A0的唯一不變集A0={(0,0,0,0)}。類似于定理3 可知E0是全局吸引的,進而全局穩定。 定理5 設R0>1,若R1<1,則E?全局漸近穩定,即捕食者種群滅絕。 證明 設模型(3)和條件(4)的任一解為(x1(t),x2(t),S(t),I(t)),由定理2 可知,若R1<1,E?局部漸近穩定,故這里僅需證明E?是全局吸引的。易知,模型(3)可寫為下面形式 由(18)式可知 類似于定理3 的討論,可以得到E?是全局吸引的,進而全局穩定。 定理6 設R1>1, αd2>r1r,若R2<1,且 其中求F21(t)的導數有 由(20)式可知 類似于定理3 的討論,可以得到E′是全局吸引的,進而全局穩定。 本文研究一個捕食者種群染病、食餌種群具有階段結構的生態-流行病模型的動力學性質,討論了由易感捕食者種群的妊娠期引起的時滯對系統穩定性的影響。通過LaSall 原理,分別得到了模型(3)的正平衡點(地方病平衡點)和邊界平衡點全局吸引的充分條件。由定理3 可知,若R2> 1 且(H1)成立,即幼年食餌為捕食者提供了足夠的食物時,食餌種群和捕食者種都會持續生存,即疾病轉化為地方病。由定理4 可知,若R0<1,食餌種群和捕食者種群均走向滅絕。由定理5 可知,若R0> 1 且R1< 1,食餌種群將永久持續生存但捕食者種群將走向滅絕。由定理6 可知,R1> 1, R2< 1 且(H2)成立,食餌種群和易感捕食者種群將會持續生存,而染病捕食者種群將走向滅絕,即傳染病將停止蔓延。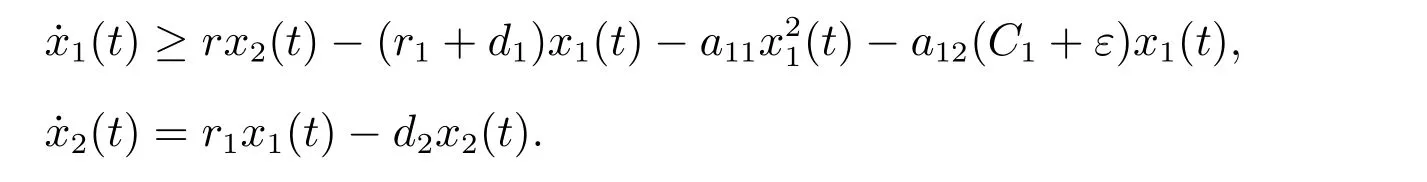
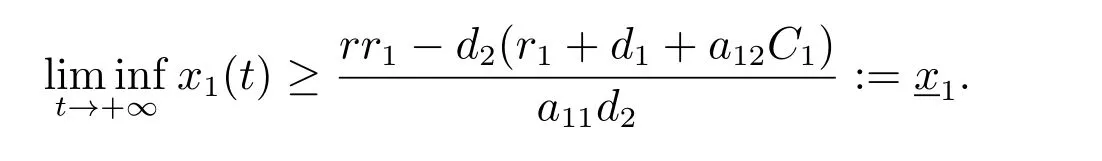
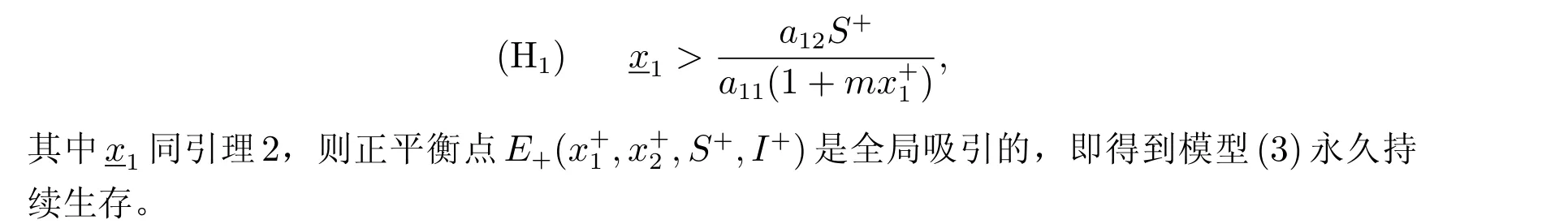

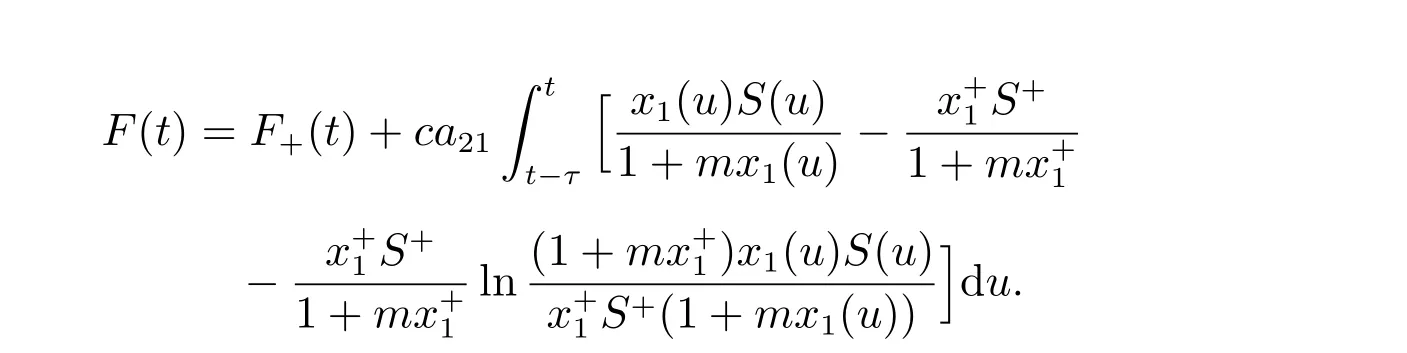

2.2 邊界平衡點的全局穩定性
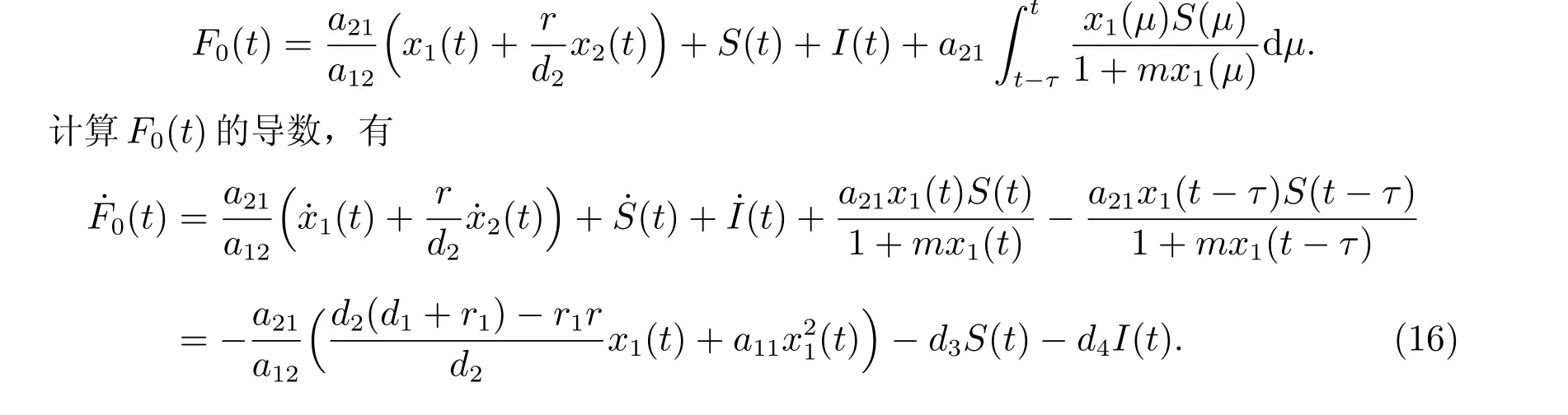

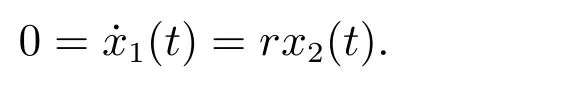


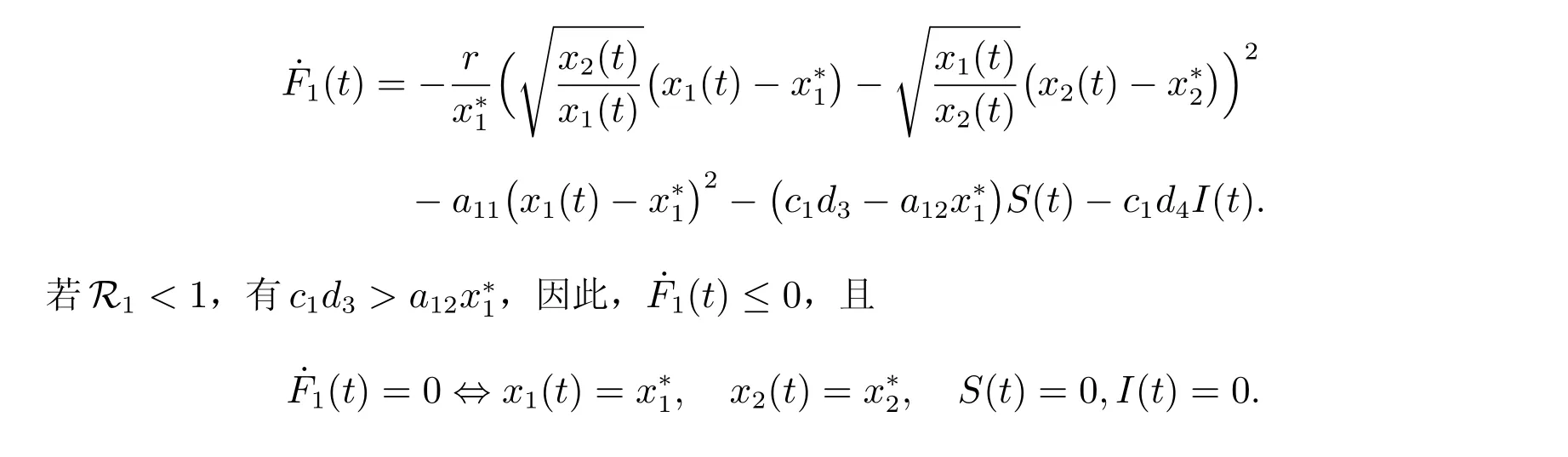

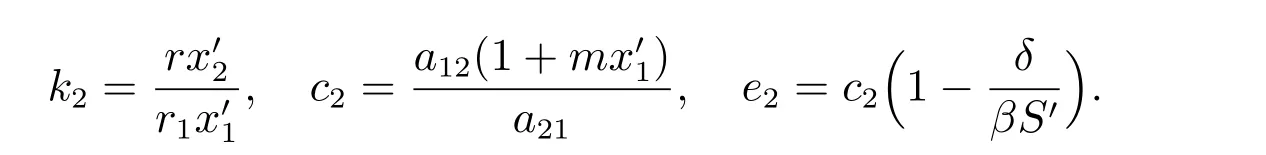
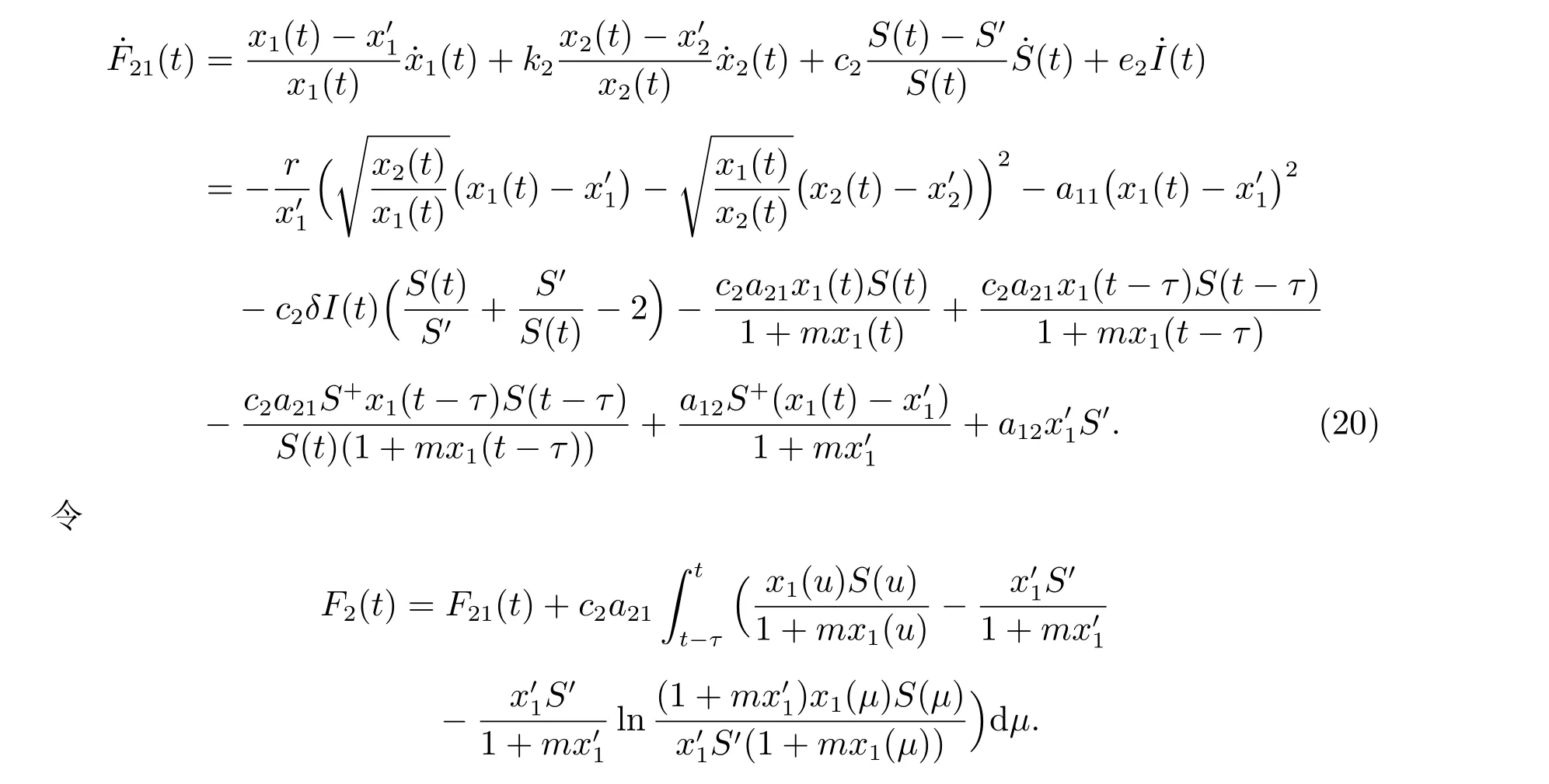
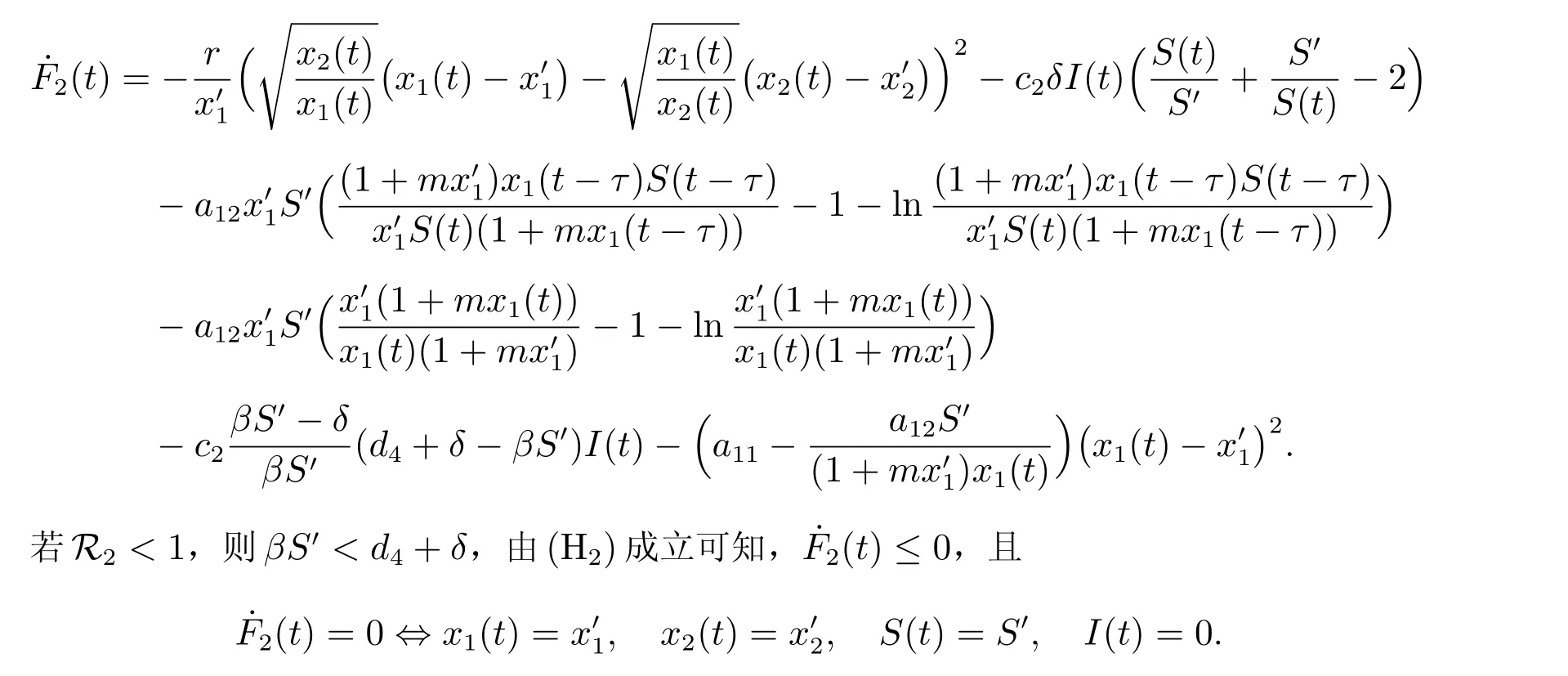
3 討論

