基于多層感知器神經網絡的燃煤電站SCR脫硝系統建模

黃鎮柯，金志遠，朱恒毅，劉宇濃，譚 鵬

（1.廣東省能源集團有限公司沙角C電廠，廣東 東莞 523900；2.華中科技大學能源與動力工程學院煤燃燒國家重點實驗室，湖北 武漢 430074）

0 引言

為控制氮氧化物（NOx）排放，選擇性催化還原（SCR）技術在燃煤電站獲得廣泛應用［1，2］。電站SCR脫硝系統通過控制噴氨閥門開度來調節出口NOx的排放濃度，是一個典型的大慣性延遲系統。過量噴氨會造成氨逃逸量增加，與煙氣中的硫發生反應產生硫酸氫銨，導致下游空預器堵塞，威脅電廠安全生產；噴氨不足會造成SCR 脫硝系統脫硝效率降低，影響電廠運行環保性［3，4］。然而隨著可再生能源入網比例的升高［5］，燃煤機組的調峰定位越來越清晰［6-8］，頻繁的機組負荷大范圍變化使得采用傳統PID 控制不能滿足SCR脫硝系統的高效安全運行［9，10］，因此，研究開發更精確、更快速的噴氨控制方法具有重要意義［11-13］。

建立準確可靠的SCR 模型是控制的基礎，為實現SCR脫硝系統的精確噴氨控制必須掌握系統的動態特性，建立合適的動態模型。目前，SCR脫硝建模方法可分為基于催化化學反應機理的機理建模［14］和基于運行數據的黑箱建模［15］，其中黑箱建模方法主要是利用統計方法或機器學習，如神經網絡［16，17］、支持向量機［18，19］等方法，采用大量運行數據進行模型訓練，由于其相對機理建模具有模型精度高、建模周期短的優勢，得到了較多的關注。

劉吉臻等［20］將多尺度核函數、滑動窗口法和偏最小二乘法結合起來，提出了自適應多尺度核偏最小二乘法，并將其利用在SCR 脫硝系統穩態建模上。秦天牧等［21］分別使用機理建模、支持向量機、反向傳播（back propagation，BP）神經網絡和偏最小二乘法對SCR 脫硝系統進行動態建模，并比較了4 種模型的性能差別。周洪煜等［22］引入動態結構的RBF 神經網絡在SCR 脫硝建模問題上，并提出了相應的噴氨控制系統。

本文以某660 MW亞臨界燃煤機組SCR脫硝系統為研究對象，利用歷史運行數據，建立基于多層感知器神經網絡（MLP）的SCR 脫硝系統預測模型，旨在為SCR噴氨控制器設計與優化提供依據。

1 研究對象與方法

1.1 研究對象

本文研究對象為某660 MW 亞臨界燃煤機組，由美國ABB-CE公司設計生產，類型為亞臨界參數、單汽包中間再熱、控制循環鍋爐，鍋爐最大連續蒸發量為2 100 t/h，膜式水冷壁，單爐膛四角雙切圓燃燒。SCR系統采用液氨作為還原劑，液氨氣化后經稀釋風機稀釋，由噴氨格柵送入SCR脫硝反應器入口，與煙氣混合后，在催化劑作用下與煙氣中的NOx發生選擇性催化還原反應。該脫硝系統采用V2O5-WO3/TiO2型的蜂窩式催化劑，催化劑分3層布置反應器內。

SCR 脫硝系統出口NOx值受很多因素影響，主要因素有負荷、煙氣流量、給煤量、SCR 脫硝系統入口NOx值、噴氨閥門開度、SCR 脫硝系統溫度、煙氣含氧量等［23，24］，其中控制變量為噴氨閥門開度，最主要的外部擾動包括SCR 脫硝系統入口NOx值以及煙氣流量、SCR 脫硝系統溫度、催化劑活性等。催化劑活性是一個長周期衰變過程，難以監測；煙氣流量、SCR 脫硝系統溫度與負荷密切相關。綜合考慮以上因素，本文所建立的SCR 脫硝系統預測模型輸入為：當前及過去時刻的①負荷，②SCR 脫硝系統入口NOx值，③噴氨閥門開度，④SCR 脫硝系統出口NOx值；模型輸出為：下一時刻的①SCR脫硝系統出口NOx值。本文共采集了1個月的運行數據，前一周數據用于訓練，后三周數據用于驗證模型穩定性。數據采樣周期為10 s，訓練數據集總長度為69 121，各參數變化范圍如表1所示。

表1 各參數單位及變化范圍Table 1 Each parameter unit and variation range

1.2 多層感知器神經網絡

多層感知器神經網絡［25，26］（MLP）的概念最先由Rosenblatt 于1952 年提出。多層感知器神經網絡是人工神經網絡的一種，一般由一個輸入層、幾個隱藏層和一個輸出層組成。人工神經網絡［27，28］由一組突觸連接構成，每個連接都有對應的權重，所有輸入經過加權之后與偏置相加，通過激活函數來轉化輸出，使得其幅度范圍縮小到有限值。其數學表達式為：

式（1）中，x為輸入值，和為第1層的權值，σ1為第1層的激活函數，神經網絡的輸出是最后一層的值zm。

1.3 基于多層感知機的SCR脫硝系統預測建模

為了避免各輸入參數由于數量級和變化范圍不同所導致的建模效果不佳，對輸入參數進行歸一化處理。引入EarlyStopping［29］方法避免過擬合，該方法可根據指定的評價標準及時停止模型的訓練，當連續n代訓練模型的評價低于之前訓練的最好結果時，立即停止模型的訓練，這樣就可以避免繼續訓練導致誤差繼續增大，激活函數選用線性整流函數（ReLU），采用Adam 優化器對MLP 神經網絡模型進行訓練［30-34］。Adam 是一種基于低階矩自適應估計的一階梯度隨機目標函數優化算法，該方法易于實現，計算效率高，內存需求少，非常適合于數據或參數較大的問題，同時也適用于非平穩目標和非常嘈雜或稀疏梯度的問題。

使用均方誤差（MSE）評價標準對模型進行評價，其公式為：

2 結果與討論

2.1 基于多層感知機的SCR脫硝系統預測建模

采用基于多層感知機對SCR脫硝系統預測建模需對時間步長、網絡層數、隱藏層節點數及訓練批次數據量大小進行優化。

時間步長調參結果如圖1所示，計算時模型采用2個隱藏層，每個隱藏層節點數為5。

由圖1 可以看出，時間步長設置太小或太大都會導致MSE較大，當時間步長為3時，訓練集和測試集的MSE 較小。在保證模型精度的情況下，考慮計算所需時間和資源，最終選擇模型的時間步長為3。

圖1 時間步長調參結果Fig.1 Parameter adjustment results of time step-length

神經網絡隱藏層數量優化如圖2 所示，模型的隱藏層節點數為5，時間步長為3。

圖2 隱藏層個數調參結果Fig.2 Parameter adjustment results of the number of hidden layers

由圖2 可以看出，隱藏層個數除了1 層之外，其他2至5層MSE誤差均相差不大，在保證模型精度的情況下，考慮計算所需時間和資源，最終選擇隱藏層個數為2。

神經網絡每個隱藏層節點數優化如圖3所示，隱藏層個數為2個，時間步長為3。由圖3可以看出，每個隱藏層個數為1個和2個時，模型效果很差，驗證集MSE誤差分別為31和29，當隱藏層節點數在3個至5個時，模型的效果提升明顯，驗證集MSE 誤差分別為0.189、0.191和0.193，因此確定最終每個隱藏層節點數為3個。

圖3 不同節點數調參結果Fig.3 Parameter adjustment results of the number of different nodes

經過對模型參數的調整，最終確定多層感知器結構為：時間步長為3，隱藏層數為2，隱藏層節點數為3，激活函數選用ReLU，其訓練過程如圖4 所示，可以看出，在第12 代-15 代的評價指標已不下降，并在50 代時停止了訓練。

圖4 MLP訓練過程Fig.4 Training process of MLP

圖5顯示了模型在測試集上的預測效果和誤差分布，可以看出，預測值與實際值基本吻合，相關系數達到了0.99，絕對誤差在0 附近波動，波動范圍不大，說明訓練出來的模型有很好的預測能力。

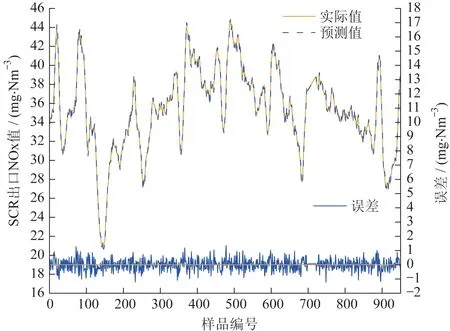
圖5 SCR出口NOx值預測效果Fig.5 Prediction effect of NOx concentration at SCR outlet

圖6為測試集的預測值與實際值之間誤差的頻率分布圖，可以很明顯地看出測試集的誤差呈期望值為0 的正態分布，約有78.78%測試集樣本的誤差絕對值位于±0.5 mg/Nm3之間，有18.5%測試集樣本的誤差絕對值位于±0.5 mg/Nm3至±1 mg/Nm3之間。

圖6 MLP模型訓練誤差頻率Fig.6 Training error frequency of MLP model

2.2 基于多層感知機的SCR脫硝系統模型階躍測試

為進一步驗證模型的效果，針對多層感知機模型還做了階躍測試，以驗證不同特征變化下，SCR 出口NOx值的響應情況，具體階躍效果如圖7所示。

圖7 展示了SCR 噴氨閥門開度特征階躍效果，針對不同的SCR 噴氨閥門開度階躍幅度，模型均做出合理且平滑的響應。SCR噴氨閥門開度階躍+0.5%，SCR出口NOx值降低-0.36 mg/Nm3，SCR 噴氨閥門開度階躍+1%，SCR 出口NOx值降低0.72 mg/Nm3，SCR 噴氨閥門開度階躍+1.5%，SCR 出口NOx值降低0.36 mg/Nm3，SCR 噴氨閥門開度階躍+0.5%，SCR 出口NOx值降低1.09 mg/Nm3，SCR 噴氨閥門開度階躍-0.5%，SCR 出口NOx值升高0.37 mg/Nm3，SCR 噴氨閥門開度階躍-1%，SCR 出口NOx值升高0.74 mg/Nm3，SCR 噴氨閥門開度階躍-1.5%，SCR出口NOx值升高1.1 mg/Nm3。

圖7 MLP模型特征階躍響應Fig.7 Features step response of MLP model

3 結論

本文以某660 MW 亞臨界燃煤鍋爐為研究對象，建立了基于多層感知器神經網絡的SCR脫硝系統預測模型。結果表明，MLP 訓練模型在測試集上的均方誤差為0.189，相關系數達到了0.99，同時針對SCR 噴氨閥門開度特征的階躍變化也作出了合理的響應，所建立的模型可用于SCR噴氨控制器設計與優化。