海洋鉆井隔水管系統動力學行為研究

李 旭， 朱志強， 馮穎韜， 趙 琥， 溫達洋， 山永林， 林黎明

1中海油田服務股份有限公司 2北京科技大學機械工程學院 3中國科學院力學研究所流固耦合系統力學重點實驗室

0 引言

隔水管系統作為深水油氣開采裝備的重要組成部分，需要面對復雜海洋環境和氣候條件的挑戰。關于海洋隔水管動力學行為的理論研究最早始于1970年代，國外學者們通過Euler-Bernoulli梁的四階微分方程來描述隔水管微元體的受力狀態，建立了海洋隔水管的力學模型[1- 2]，也有學者將隔水管系統分成若干個部分，并通過一系列彈簧阻尼單元來連接模擬[3]。基于建立的力學模型，分析了隔水管軸向載荷和橫向載荷的非線性耦合[4]，提出了一種考慮流體和結構不確定性的海洋結構響應統計特性評價方法[5]。國內學者們則對影響隔水管振動的各種因素進行了探討[6]，建立了基于海洋環境和鉆井工況耦合作用下的隔水管系統動力學控制方程[7- 8]，并基于隔水管力學性能實驗，提出了深水鉆井隔水管的“三分之一效應”[9]。還有部分學者分析了隔水管系統的固有頻率[10]以及主共振的穩定性[11]，并利用接觸單元模擬內外管接觸的約束條件[12]。此外，Abaqus及其海洋環境模塊Aqua被采用來對建立的隔水管-鉆柱的管中管模型進行了動態響應分析，并將模型導入Isight優化軟件，進行了基于可靠度分析的多目標優化設計[13]。

基于上述文獻調研可知，對于海洋鉆井隔水管系統動態響應的研究一直屬于本領域的熱點問題，而對于管柱系統這種連續體的振動問題，有限元分析又是最為有效的手段。然而，在已發表的論文中，關于隔水管系統動力學建模以及有限元分析的求解過程都未見詳盡說明，容易引起困惑。因此，本文旨在詳細介紹海洋鉆井隔水管有限元建模及其求解流程，并進行隔水管單管的動力學行為研究。

1 海洋鉆井隔水管系統的動力學建模

海洋鉆井隔水管系統動力學建模是在所提出的基本假設的基礎上，通過開展對隔水管系統動能、勢能、外力做功三方面的數學描述，并最終基于Hamilton原理整合成為一個完整的動力學模型。

1.1 基本假設

(1)假設隔水管變形均在彈性范圍內。

(2)假設隔水管是由均質、各向同性、線彈性的材料制成。

(3)假設隔水管變形和變形角是小量的，屬于大應變小變形。

(4)暫不考慮鉆柱對隔水管的碰撞影響。

1.2 隔水管系統動能

海洋鉆井隔水管可以簡化為彈性梁，其在海洋環境載荷的作用下將發生橫向變形，從隔水管中取出一個單元體，其物理模型如圖1。

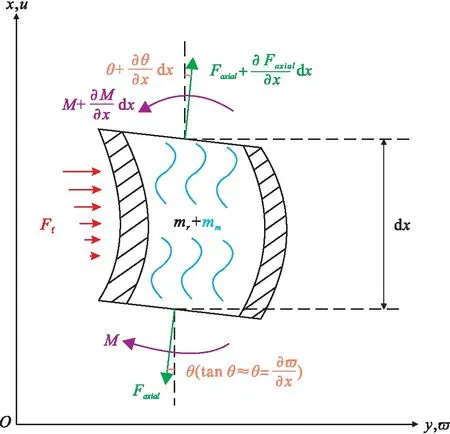
圖1 隔水管單元受力分析圖

(1)

式中：mr—單位長度隔水管質量，kg;mf—單位長度的環空鉆井液質量,kg;?(x,t)—隔水管單元的橫向偏移，m。

1.3 隔水管系統勢能

勢能包括應變能和任何保守外力的勢能。根據應變應力關系得應變能為：

(2)

式中：E—隔水管的彈性模量,MPa。

另一方面，作為隔水管的內力，其軸向力是由隔水管的頂張力以及浮力共同決定的，可表示為：

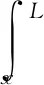
(3)

式中：Rtop—頂張力與隔水管與鉆井液重量之和的比值，N/(m·kg);L—代表隔水管的總長，m;fb—代表浮力因子,無綱量;g—重力加速度，9.8 N/kg。

而當隔水管發生彎曲時，其軸向力將在橫向上做功，當引入小應變大變形假設時，該軸向力做功可表示如下：

(4)

所以，總的勢能可表示為：

V(x,t)=V1(x,t)+V2(x,t)

(5)

1.4 外力做功

在不考慮鉆柱的情況下，隔水管所受的外力主要來源于海洋環境載荷，根據莫里森方程可知海洋環境載荷Ff(x,t)包括拖曳力FD(x,t)和慣性力FI(x,t)兩部分，即：

Ff(x,t)=FD(x,t)+FI(x,t)

(6)

(7)

(8)

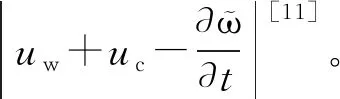
1.5 海洋鉆井隔水管動力學模型整合

根據Hamilton原理的數學表達式：

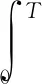
(9)

在一個海浪周期內，該隔水管系統的總能量可以描述為：

(10)

此外，隔水管系統的頂部通過轉動剛度為Kt的撓性接頭與平臺連接，因此會隨平臺發生漂移；而隔水管系統底部則通過另一個撓性剛度為Kb的柔性接頭固定在井口；因此，隔水管系統的頂、底處的初始條件和邊界條件可分別表示為：

(11)

(12)

2 海洋鉆井隔水管系統的有限元模型

首先，作為有限元分析的第一步，所建立的動力學模型需要被離散化。為了實現離散化模型的目的，采用彎曲梁單元的Hermite三次插值函數作為形函數，將包含形函數的位移近似解代入式(11)的動力學運動方程并化簡得：

(13)

海洋隔水管系統的有限元模型表示為：

(15)

式中:[Mrm]—隔水管自身質量以及鉆井液附加質量引起的質量矩陣；[MfI]—慣性力衍生的質量矩陣；[CfD]—拖曳力衍生的阻尼矩陣；[KEI]—彎曲應力引起的剛度矩陣；[KFa]—軸向力引起的剛度矩陣；[S]—位移列向量；[f]—外力列向量。

3 海洋鉆井隔水管系統的動力學行為研究

采用Newmark積分法對建立的有限元模型進行求解，得到海洋鉆井隔水管系統的動態響應。為研究鉆井隔水管系統在海洋環境載荷作用下的動態響應，基于所建立的有限元模型，通過MATLAB編程對水深500 m的隔水管系統進行數值模擬研究。具體參數如表1所示。

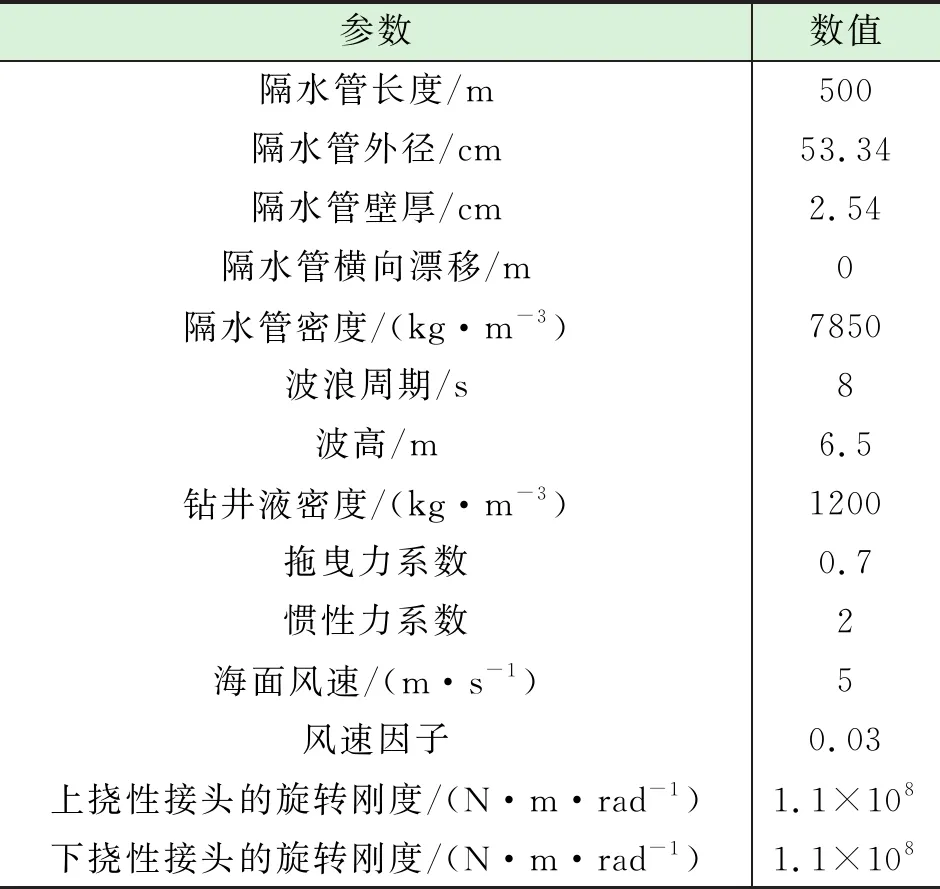
表1 隔水管具體參數表

對于一個水深為500 m的海域，海浪的影響主要集中于靠近海面的區域，且呈周期性變化；而海流的速度分布與時間無關，但會在海洋中上部摩擦深度所對應的位置發生一個突變[16]。

由于本文考慮的海洋環境載荷具有周期性，因而在其影響下的隔水管系統的動態響應最終也將達到動態穩定狀態，而其判斷標準是上、下撓性接頭的轉動均滿足穩定的周期性特征。

隨后，在確保隔水管系統的上、下撓性接頭的轉動達到其動態穩定狀態下對隔水管壁厚、頂張力、浮力因子、海流流速、海浪波高等關鍵因素進行分析。

3.1 隔水管壁厚的影響

在實際應用中隔水管的標準壁厚大多為2.54 cm，因此分別選取標準壁厚、標準壁厚的2倍和3倍進行對比。從圖2可以看出，隔水管壁厚對隔水管的動態響應有著顯著影響。從左側子圖可以看出當隔水管壁厚增加時，隔水管的橫向偏移和振動幅度都得到了有效抑制，從中間子圖和右側子圖也可以發現隨著壁厚的增加，彎曲應力和偏移撓度角都逐步減小。

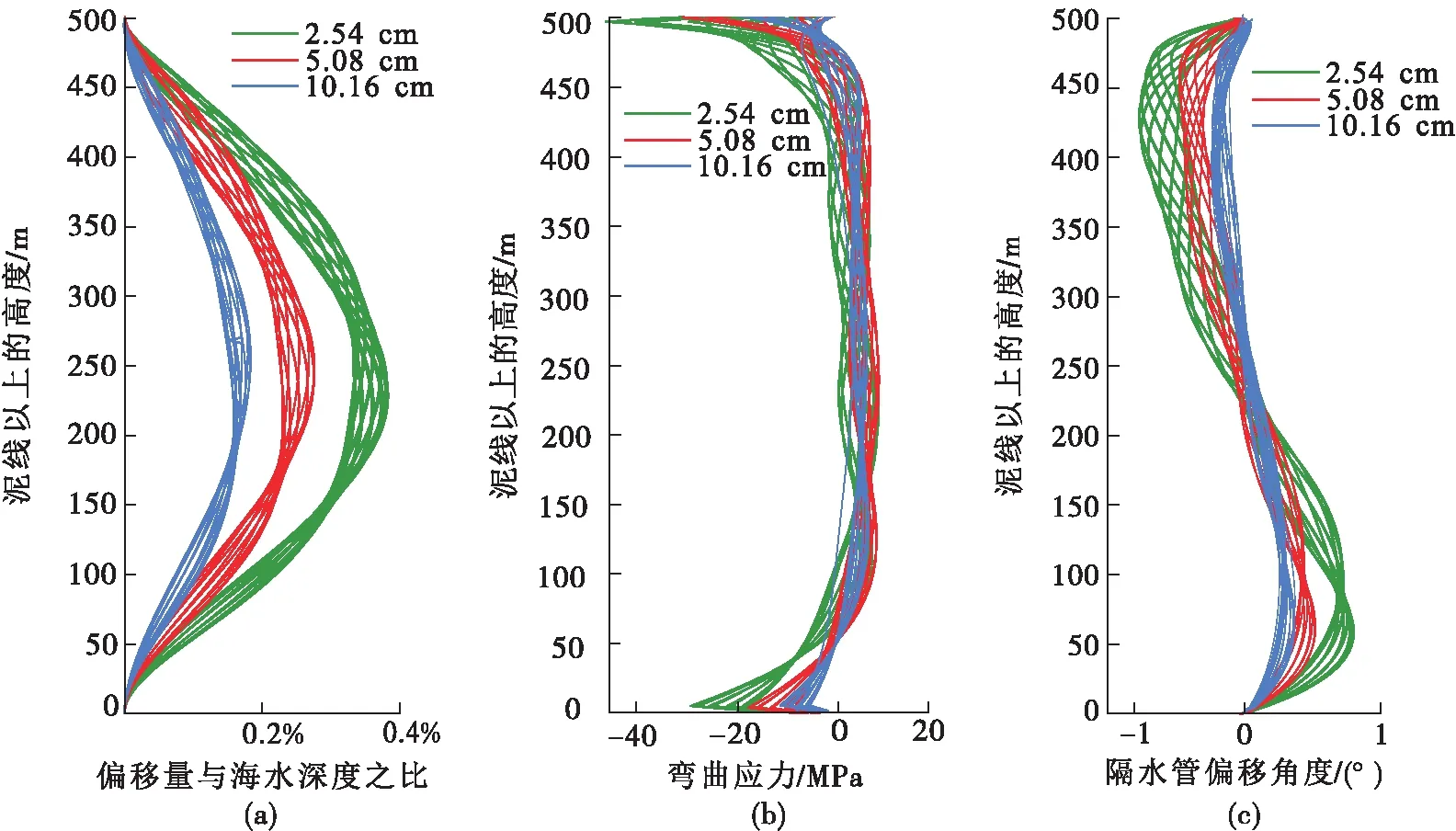
圖2 隔水管壁厚的影響

3.2 頂張力的影響

比較頂張力比分別為1.1、1.3和1.5的三種情況。從圖3(a)子圖和(c)子圖可以明顯看出，一旦施加較高的頂張力，隔水管的橫向偏移和偏轉角度都可以得到有效控制。但是猶如圖3(b)所示，增大頂張力會導致彎曲應力增加，所以預設頂張力也不是越大越好。

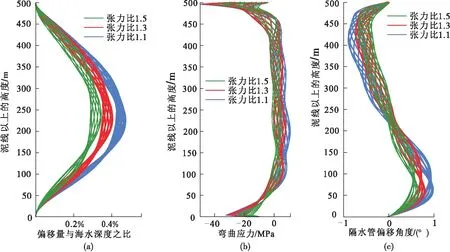
圖3 頂張力的影響

3.3 浮力因子的影響

浮力系數主要取決于隔水管外掛浮力塊的設計策略。比較了浮力因子為0.5、0.7和0.9三種不同的方案。由圖4可知，為降低對鉆井平臺的升力要求，在隔水管外部增加浮力塊時，隔水管的橫向偏移、彎曲應力以及偏移角度都明顯增大。因此，為了有效控制隔水管的偏轉，在鉆井平臺提升能力的允許范圍內，建議選取浮力系數較小的浮力塊設計策略。

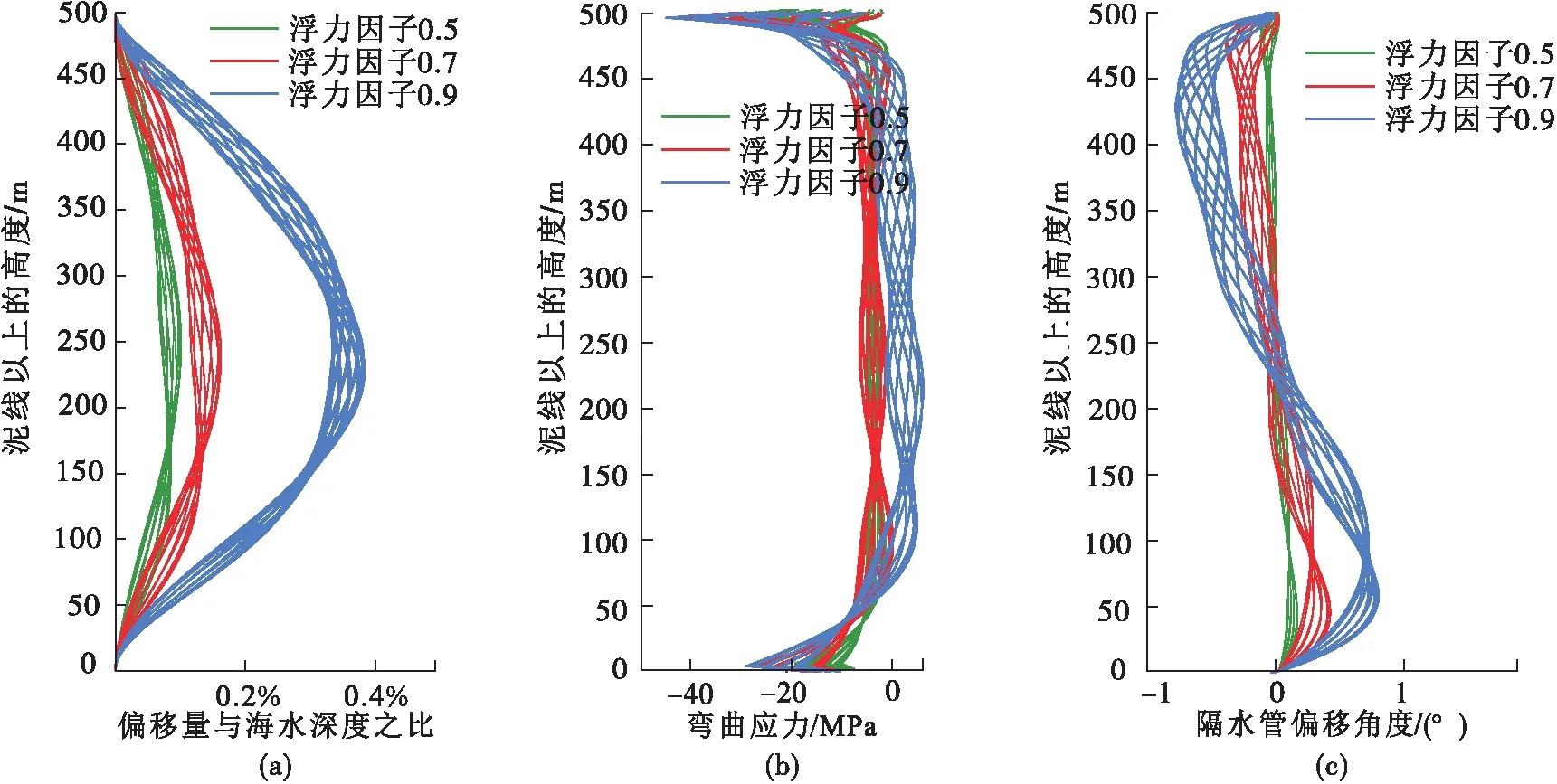
圖4 浮力因子的影響

3.4 海洋環境載荷的影響

根據莫里森方程求解出海流水平運動速度Vc，分別比較0.5Vc，1.0Vc，1.5Vc三種不同海流速度下隔水管系統的動態響應情況，如圖5所示。海流流速不僅影響隔水管頂部和底部的彎矩，對隔水管整體的振動也有著顯著影響，雖然海流的速度會隨著海深深度的增加逐步降低，但海流流速增加仍然會導致隔水管的橫向偏移和偏轉角度的增大。此外，海浪波高的增加對隔水管橫向偏移的影響不明顯，主要影響隔水管頂部，波高的增大將使得其彎曲應力和偏轉角度增大，但海浪波高對隔水管動態響應的影響程度低于海流流速的影響。整體而言，為了保證隔水管的使用安全，針對不同的海洋環境進行隔水管系統設計時，要注意調整頂張力、浮力塊配置等可控參數，來加強對隔水管系統橫向偏移的抑制。

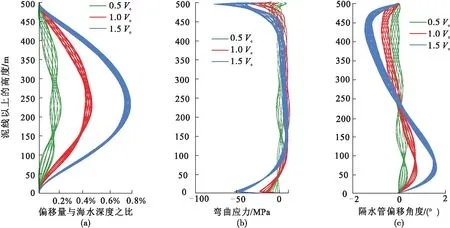
圖5 海流流速的影響

5 結論

(1)本文利用Hamilton原理推導了隔水管系統在海洋環境載荷作用下的動力學模型，利用Hermite三次插值函數作為形函數，將動力學模型轉化成有限元模型，并采用Newmark積分法對有限元模型進行了數值求解分析了不同參數對隔水管系統動態響應的影響。

(2)波浪的影響集中在靠近海面的區域，波高對隔水管動態響應的影響不明顯，但波高的增加會導致隔水管頂部彎曲應力和偏轉角度的增加。海流流速的增加會加劇隔水管的橫向偏移，其對隔水管動態響應的影響顯著強于波浪的影響。

(3)對于隔水管本身而言，厚壁隔水管的動態穩定性更好。而頂張力越大，隔水管的橫向偏移越小，但大的頂張力會引起彎曲應力和偏轉角度的增大；此外，隨著浮力的增大，隔水管的橫向偏移、彎曲應力和偏轉角度都會增大；因此，在確保海洋鉆井平臺提升能力的前提下，應盡量選取浮力系數較小的浮力塊作為設計策略。