600 MPa 鋼筋滾壓套筒灌漿連接參數化分析

張新，張珊珊，孫志剛，鄭永峰，*，毛安琪

(1. 山東建筑大學土木工程學院，山東濟南 250101；2. 山東兗州建設總公司，山東 濟寧 272100)

0 引言

裝配式混凝土結構預制構件的豎向可靠連接是其推廣的關鍵，其中縱向鋼筋的牢靠連接尤為重要。套筒灌漿連接和漿錨搭接是縱向鋼筋的主要連接方式，前者幾乎不受鋼筋直徑以及建筑高度的約束，有更廣泛的適用范圍。 有些學者對灌漿套筒的研究較早，而且偏向于對套筒構造的研究。 EINEA 等[1]設計了4 種不同類型的全灌漿套筒，其中只有兩端采用鋼環的套筒類型能夠滿足接頭的性能要求。LING 等[2]采用無縫鋼管制作了兩種不同構造的全灌漿套筒——錐形頭套筒(Tapered Hard Sleeve，THS)與焊接鋼筋套筒(Welded Bar Sleeve，WBS)，其中THS 套筒兩端縮口，黏結強度更高。 HENIN 等[3]提出一種新型灌漿套筒構造，即在套筒內壁表面布滿螺紋，通過接拔試驗與有限元數值模擬，得到套筒長度取13 倍鋼筋直徑時可以保證接頭試件的承載力要求。 SEO 等[4]提出一種新型鋼筋連接方式——墩頭套筒(Head-Splice Sleeve，HSS)，通過單向拉伸試驗，得出HSS 接頭抗拉強度滿足要求。

隨著國內混凝土裝配式建筑的興起，人們對鋼筋套筒灌漿連接試件的研究逐漸增多。 吳小寶等[5]設計了36 個鋼筋接頭試件進行單向拉伸和單向重復拉伸試驗，得到灌漿料齡期和鋼筋種類對接頭試件受力性能的影響。 黃遠等[6]設計制作了14個鋼筋半套筒灌漿連接試件，通過靜力拉伸試驗，得到試件的3 種破壞形態并分析了每種破壞形式的承載力。 鄭永峰等[7]對31 組鋼筋套筒灌漿連接件進行了單向拉伸試驗與理論分析，研究了套筒環肋數量、環肋凸起高度以及環肋間距對鋼筋套筒灌漿連接構件黏結性能的影響規律。 吳濤等[8]對20 個套筒灌漿連接件進行單軸拉伸試驗，得出套筒筒壁的應變隨鋼筋錨固長度的增加而減小，隨鋼筋直徑的增大而增大，并通過對比有限元模擬與試驗結果，得出ANSYS Workbench 有限元軟件可以較準確地模擬鋼筋接頭構件的力學性能。 余瓊等[9]研究了不同直徑的HRB400 帶肋鋼筋與灌漿料的黏結滑移關系，給出各個特征點的黏結強度和滑移值的計算公式。 王寧等[10]根據鋼筋直徑和搭接長度以及套筒壁厚和端部約束方式4 種參數，制作了9 組節點試件，在試驗結果的基礎上，利用ABAQUS 有限元軟件建立數值模型，通過結果比對，驗證了ABAQUS用于研究鋼制套筒灌漿連接件力學性能的可靠性。鋼筋強度直接影響著建筑物的安全性，隨著行業對建筑物抗震等級提出的更高要求，HRB500 及以上級別鋼筋在高層混凝土建筑上的使用量不斷上升。李艷艷等[11]通過單向拉伸試驗，研究了直徑18、25 mm的600 MPa 鋼筋的粘結錨固性能。 高向玲等[12]推導出了新的鋼筋與灌漿料粘結強度的表達式，并提出8 倍鋼筋直徑是600 MPa 鋼筋的最優錨固長度。

目前，學者們對鋼筋套筒灌漿連接的研究多基于普通強度等級鋼筋，對500 MPa 級別以上的鋼筋接頭研究較少。 因此，采用直徑為22 mm 的600 MPa 鋼筋、高強水泥基灌漿料和變形灌漿套筒(Grouted Deformed Pipe Splice，GDPS)設計而成的試件進行單向拉伸試驗。 利用ABAQUS 有限元軟件對試驗接頭建立數值模型，將模擬得到的試件極限承載力、荷載-位移曲線等與試驗結果進行對比。在理論分析可行的基礎上，對600 MPa 鋼筋滾壓套筒灌漿連接接頭進行數值模擬與參數化分析，得出鋼筋接頭滑移規律、套筒表面應變規律以及鋼筋錨固長度與套筒內腔構造對接頭性能的影響規律。 通過對比不同參數下接頭試件的強度與變形，最終給出直徑為 18、22、25 mm 的600 MPa鋼筋適用的套筒規格。

1 試驗概況

1.1 試件設計

采用公稱直徑d 為22 mm 的600 MPa 鋼筋、灌漿料與GDPS 套筒制作了一組試件，其中套筒由Q390 無縫鋼管滾壓制成，規格為Φ57×5(外徑×壁厚，mm)，兩側分別有5 道環肋，其中套筒環肋與鋼筋橫肋間的最小差值為20 mm，滿足JGJ 355—2015《鋼筋套筒灌漿連接應用技術規程》[13]的要求。 同時，在鋼筋拉斷的套筒截面可基本保持彈性狀態，滿足JGJ 355—2015[13]的要求，即由式(1)表示為

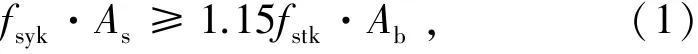
式中As為鋼套筒中部截面面積，mm2； fstk為鋼筋抗拉強度標準值，MPa；Ab為鋼筋公稱截面面積，mm2；fsyk為鋼套筒屈服強度標準值，MPa。

試件構造形式如圖1 所示，鋼筋和套筒的材料力學性能見表1。 灌漿料棱柱體標準試塊(40 mm×40 mm×160 mm)同條件養護28 d，測得抗壓強度為95.5 MPa。

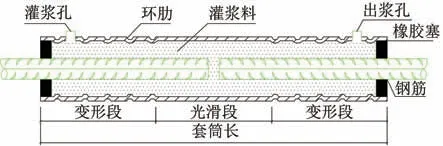
圖1 試件構造形式圖

表1 試件材料性能表

1.2 加載裝置及測點布置

單向拉伸試驗在萬能試驗機(最大量程為1 000 kN)上進行，加載速率為2 MPa/s，試件發生破壞時停止加載。 為監控加載過程中套筒的環向應變與軸向應變以及鋼筋的軸向應變，將電阻應變片貼于套筒外表面，應變片測點位置如圖2 所示。

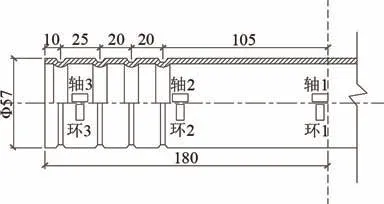
圖2 應變片測點位置圖/mm

1.3 主要試驗結果

試驗共出現兩種破壞結果，詳見表2。

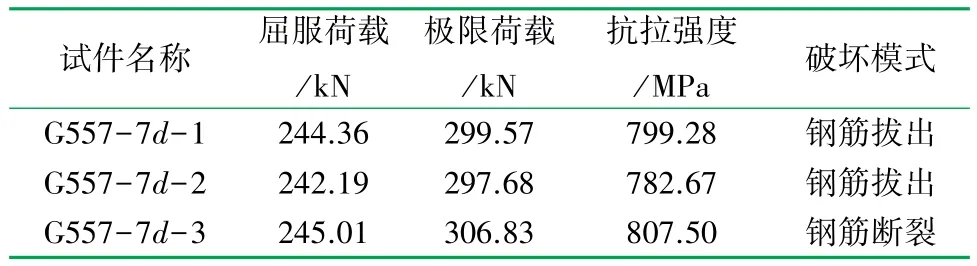
表2 試驗結果表

2 有限元分析

2.1 模型建立

鋼筋套筒灌漿連接試件構造對稱、載荷對稱，故可以等效為軸對稱模型。 鋼筋按照三折線的本構模型，初始屈服應變為0.002，應變屈服平臺為0.008，極限應變取0.2，對應的實測屈服強度、抗拉強度以及彈性模量見表1，應力應變曲線如圖3 所示。 鋼套筒采用理想彈塑性雙折線模型，應力應變關系曲線如圖4所示。 灌漿料采用ABAQUS 中所提供的混凝土損傷塑性模型(CDP 模型)，參數選取C80 混凝土的CDP模型數據，泊松比為0.2、彈性模量取33 GPa[14]。

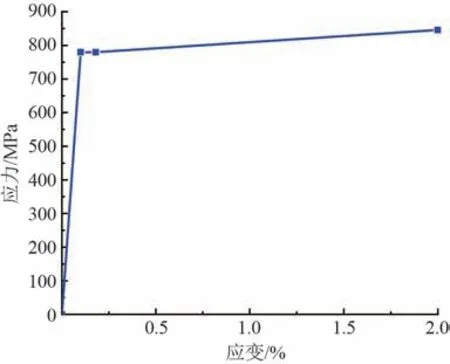
圖3 鋼筋本構曲線圖

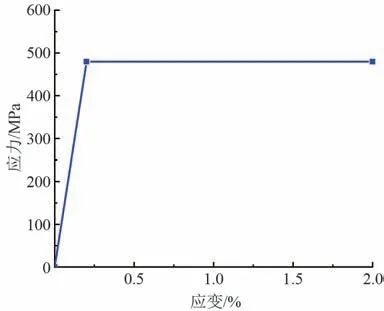
圖4 套筒本構曲線圖

鋼筋與灌漿料、灌漿料與套筒之間都是直接接觸，由于接觸作用，模型中選擇能夠有效模擬復雜接觸問題和非線性問題的ABAQUS/Explicit 分析模塊。接觸類型選擇表面與表面接觸，鋼筋與套筒分別被選作各自接觸中的主面，灌漿料被選作次面。 鋼筋、灌漿料與套筒均按照結構化的分網規則，采用的是CAX4R 二維實體單元，其為采用細網格劃分的線性減縮積分單元最常用的一種。 GB/T 1499.2—2018《鋼筋混凝土用鋼第2 部分:熱軋帶肋鋼筋》[15]規定直徑為22 mm 的鋼筋橫肋間距為9.7 ～10.3 mm，本模型取10 mm。 試件的有限元模型如圖5 所示。

圖5 試件1/4 有限元模型圖

2.2 模型校驗

為減小應力集中，將軸向力等效為均布載荷施加在鋼筋自由端。 接頭試件最大承載力及殘余變形的有限元數值模擬與試驗結果對比見表3，有限元數值模擬結果與試驗所得結果接近。

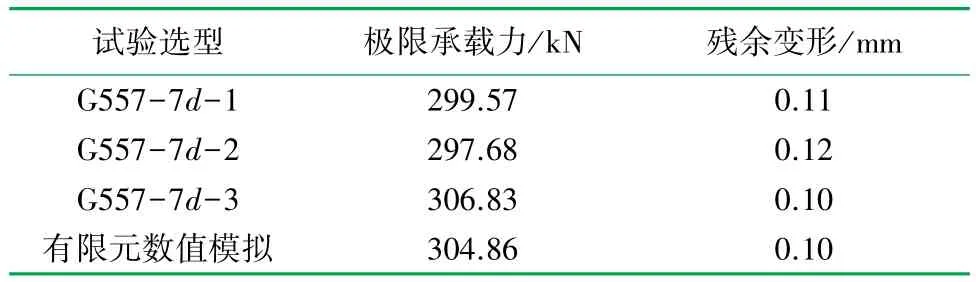
表3 試驗與有限元數值模擬結果對比表

試件G557-7d-3 的荷載-位移曲線有限元數值模擬與試驗結果對比如圖6 所示，可以看出有限元數值模擬曲線與試驗結果曲線走勢大致相同。 有限元分析的曲線沒有下降段是因為鋼筋的應力應變關系未考慮下降段，但可以通過數值模擬獲得接頭試件的屈服應力、極限承載力等主要特征[14]。

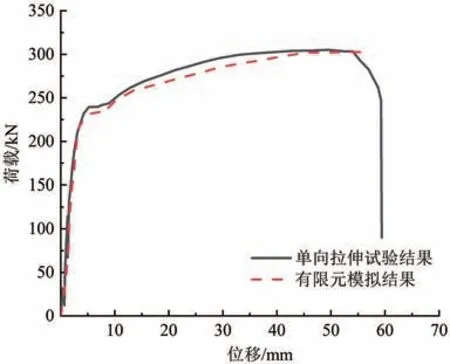
圖6 荷載-位移曲線對比圖

表3 和圖6 表明，模型能較準確地模擬鋼筋套筒灌漿連接試件的極限承載力、殘余變形以及荷載-位移曲線，可用于600 MPa 鋼筋套筒灌漿連接接頭的參數化分析。

3 600 MPa 鋼筋接頭參數化分析

在建模合理的基礎上，改變模型中鋼筋錨固長度、套筒環肋數量等相關參數，通過模擬得到鋼筋套筒灌漿連接試件的滑移規律、鋼筋錨固長度與套筒環肋數量對接頭性能的影響規律以及套筒表面的應變規律。 鋼筋套筒灌漿連接構件性能指標包括強度和變形兩個方面，前者要求接頭試件在鋼筋斷裂之后破壞，后者要求試件殘余變形與伸長率滿足要求。600 MPa 鋼筋的抗拉強度標準值為730 MPa[16]，鋼筋構件的有限元模型尺寸見表4。

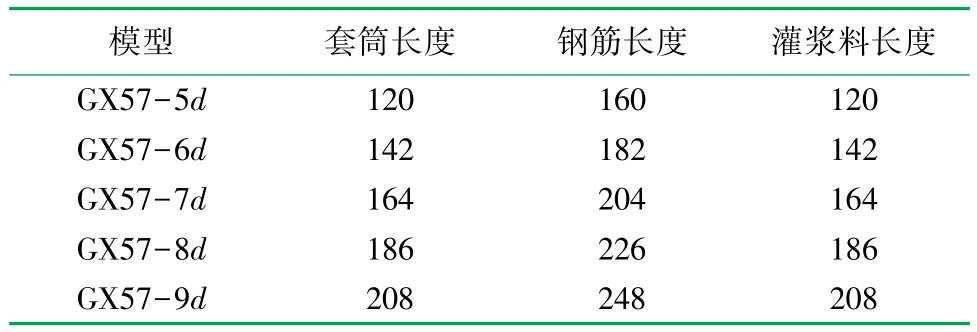
表4 鋼筋構件有限元模型尺寸表 單位:mm

3.1 鋼筋接頭滑移規律

3.1.1 鋼筋滑移規律

單向拉伸試驗中，鋼筋、灌漿料以及套筒受到荷載作用時，會因材料性能不同而產生不同變形，就會有相對滑移產生，研究三者之間的滑移規律具有深遠意義。 鋼筋應力為730 MPa 時，套筒一側不同環肋數量(3，4，5)、鋼筋錨固長度為6d 的接頭模型中鋼筋與灌漿料之間的相對位移曲線如圖7 所示，曲線圖的橫坐標為鋼筋橫肋在接頭中的位置(如圖8所示)，假定鋼筋橫肋間距為10 mm。 曲線在第5 個與第11 個鋼筋橫肋處發生突變，其中套筒邊緣處鋼筋與灌漿料的相對位移最小，套筒中部最大，第5 ～11 個橫肋之間兩者受力接近，相對滑移值較穩定，說明鋼筋錨固長度為6d 的接頭均發生鋼筋拔出破壞，不能滿足構件安全性能要求。

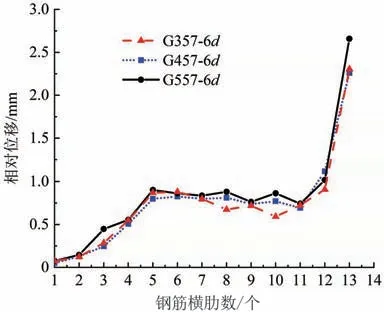
圖7 730 MPa 時鋼筋與灌漿料的相對位移曲線圖

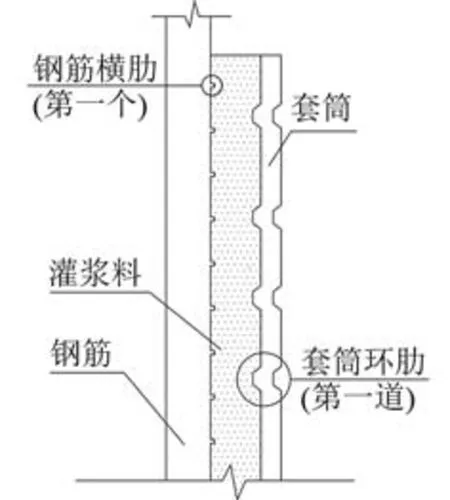
圖8 接頭的有限元構造圖

3.1.2 灌漿料滑移規律

鋼筋應力 730MPa 時，接頭模型 G357-6d 與G457-6d 的灌漿料與套筒豎向位移云圖及灌漿料沿套筒長度方向的位移曲線分別如圖9、10 所示。由圖9 可知，套筒豎向位移值很小，因此在研究灌漿料與套筒之間的相對位移規律時可不考慮該數值，直接通過灌漿料在載荷下的位移來判斷。 由圖10可得，在套筒無環肋段，曲線僅在套筒中部與第一道環肋(如圖8 所示)外側附近有發生轉折，其他位置的灌漿料位移值較接近，同時，3 道肋比4 道肋的接頭位移大了0.68 mm。 在套筒中部施加固定約束，能有效限制灌漿料產生滑動，因此曲線起始端位移較小；由于套筒環肋對灌漿料有約束作用，在套筒環肋段，灌漿料位移在第一道環肋處最小，套筒邊緣處最大，另外，環肋間灌漿料的滑移大小幾乎不受環肋數量增加的影響。

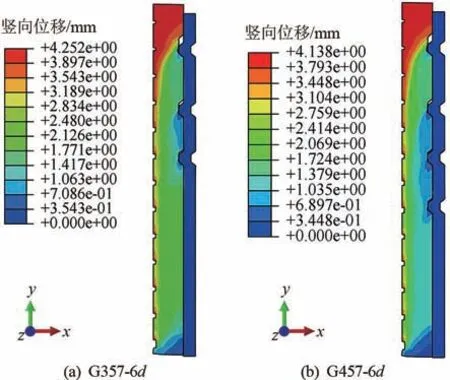
圖9 730 MPa 時套筒豎向位移云圖

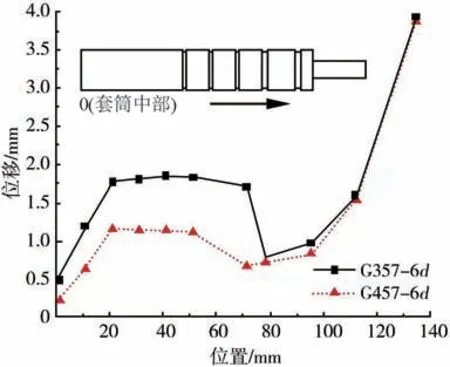
圖10 730 MPa 時灌漿料位移曲線圖

3.2 套筒表面應變變化規律

3.2.1 軸向應變規律

套筒軸向應變的測點位置如圖11 所示，鋼筋錨固長度為6d、套筒一側分別設3、4、5 道環肋的接頭模型的荷載-軸向應變關系曲線如圖12 所示。 套筒變形(有環肋)段既有拉應變也有壓應變，光滑(無環肋)段均為拉應變，且在增長過程中有3 個轉折點，分別為 115、180、250 kN，其應變值遠大于變形段的拉壓應變值。

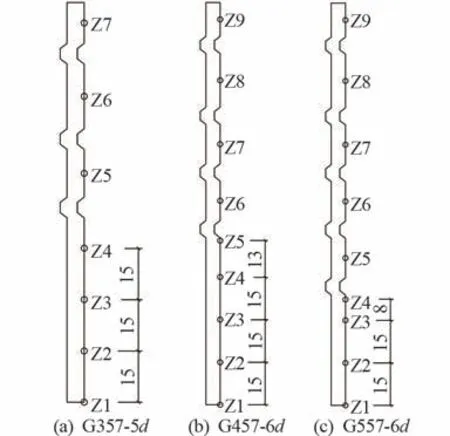
圖11 套筒軸向應變測點圖/mm

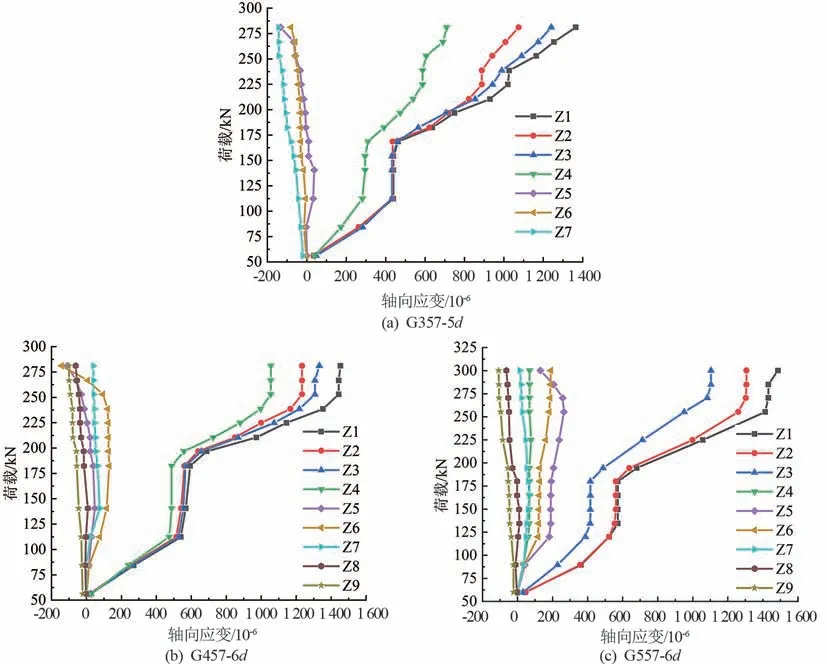
圖12 荷載-套筒軸向應變關系曲線圖

3.2.2 環向應變規律

套筒環向應變測點位置如圖13 所示，3 類接頭模型的荷載-環向應變關系曲線如圖14 所示，所用接頭模型以及測點位置均與軸向應變規律所選一致。 套筒光滑段環向應變也有3 個拐點，分別發生在載荷為113、185、245 kN 時，與同位置軸向應變拐點接近，曲線走勢與軸向應變曲線相近，且應變絕對值小于同位置處軸向應變；套筒變形段曲線無明顯轉折點，越靠近套筒邊緣其應變值越小，且數值絕對值均大于同位置的軸向應變；在單向拉伸作用下，套筒光滑段與變形段的環向應變均為壓應變。

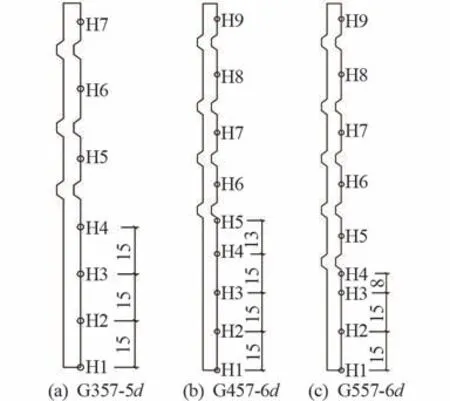
圖13 套筒環向應變測點圖/mm

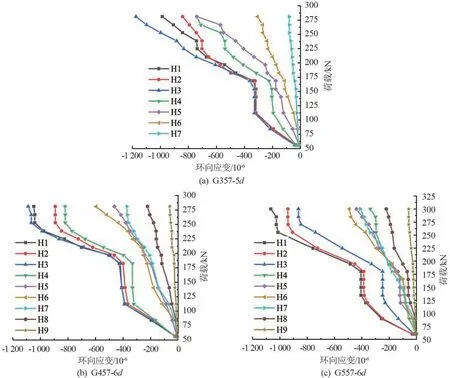
圖14 荷載-環向應變關系曲線圖

3.3 套筒環肋數量對接頭性能的影響

3.3.1 強度

套筒每側少于3 道環肋的接頭試件在荷載較小時會產生較大變形，且不能恢復原狀，不能滿足構件的安全性能要求[14]。 因此，模擬中套筒一側環肋數量最少應設置3 道。 接頭承載力與套筒環肋數量關系曲線如圖15 所示，橫坐標為套筒一側的環肋數量，中鋼筋錨固長度為5d 與6d 的模型構件，環肋數量由3 道增加到5 道，接頭承載力提高3.6%～4.2%；若由4 道增加到5 道，接頭承載力僅增強2.4%。 鋼筋錨固長度為7d 的模型構件，套筒每側4 道環肋比3 道環肋的接頭承載力提高1.9%；套筒每側5 道環肋比3 道環肋的構件承載力提高5.4%。 環肋數量由4 道增加到5 道，鋼筋錨固長度為8d 的模型構件承載力僅提高0.9%，鋼筋錨固長度為9d 的模型構件承載力提高了1.8%。因此，環肋數量的增加會因鋼筋錨固長度的不同而對構件承載力產生不同的影響，且當錨固長度超過8 倍鋼筋直徑時，環肋數量的增加對構件承載力的提升效果將有所減弱。

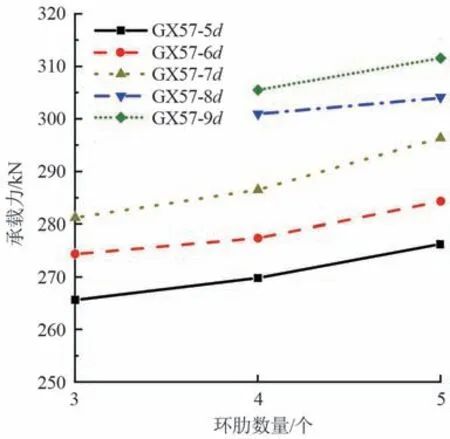
圖15 接頭承載力與環肋數量關系曲線圖

3.3.2 變形

鋼筋屈服前，鋼筋錨固長度為5d ～9d 的不同套筒環肋數量接頭的荷載-位移曲線如圖16 所示。由圖可得，鋼筋錨固長度越大，曲線越接近，說明鋼筋錨固長度越大，接頭變形的影響受套筒環肋數量下影響越小。

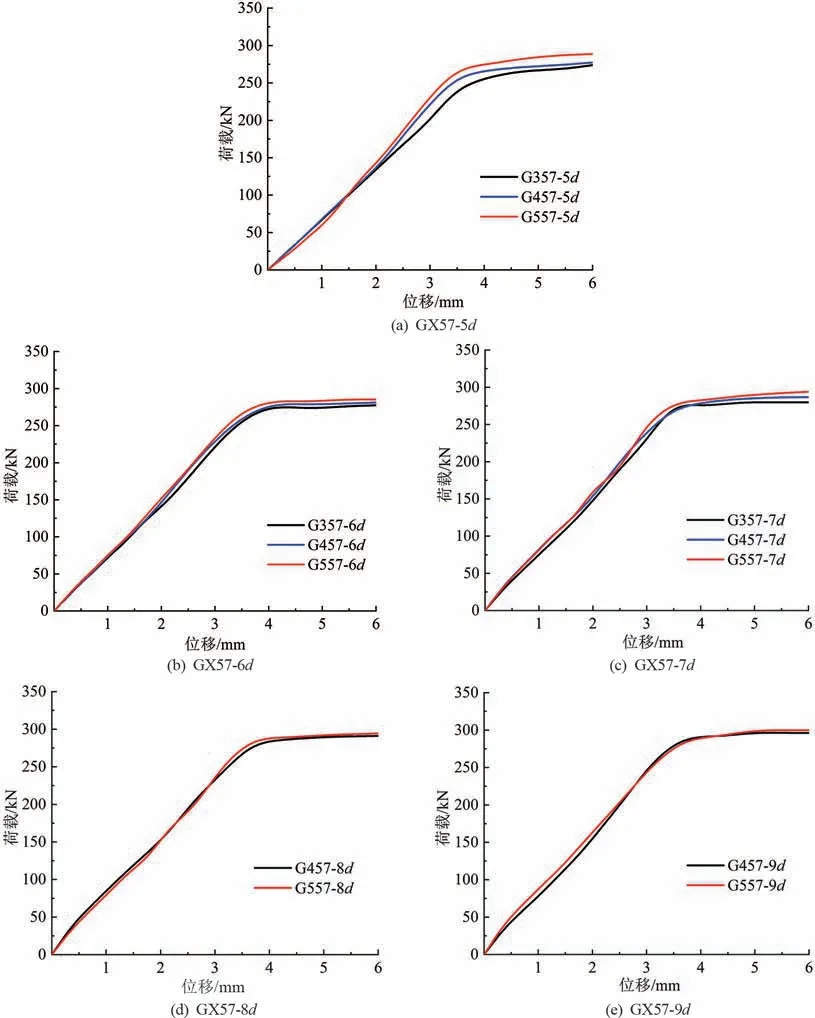
圖16 不同環肋數量接頭的荷載-位移曲線圖

按照 JGJ 107—2016《鋼筋機械連接技術規程》[17]中關于單向拉伸試驗測量殘余變形的加載制度(0～0.6fyk～0， fyk為鋼筋屈服強度標準值)，模擬得到接頭構件的殘余變形，詳見表5。 JGJ 355—2015《鋼筋套筒灌漿連接應用技術規程》[13]中3.2.6 條規定，直徑≤32 mm 的鋼筋套筒灌漿連接接頭，單向拉伸的殘余變形應≤0.1 mm。

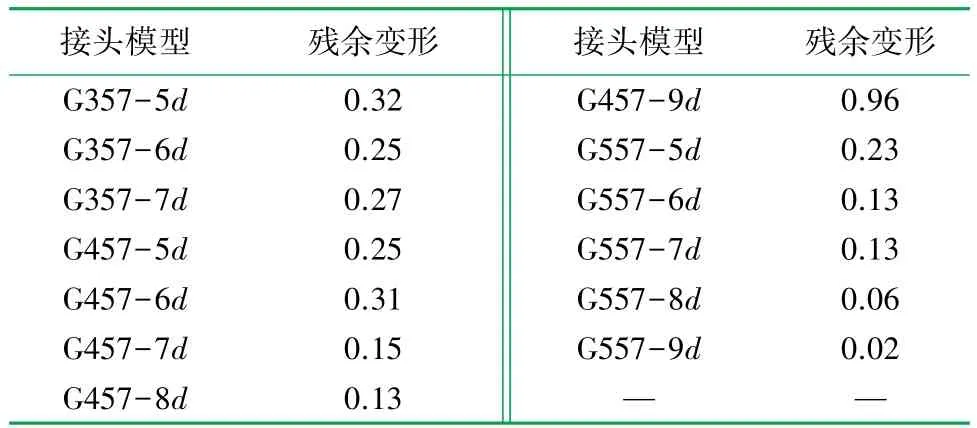
表5 接頭的殘余變形數值模擬結果表 單位:mm

由表5 可知，G357-Xd 的接頭模型殘余變形均＞0.1 mm，不能滿足600 MPa 鋼筋的安全連接；套筒每側設置4 道環肋時，僅鋼筋錨固長度達9d 的接頭模型的殘余≤0.1 mm，滿足規范殘余變形要求；套筒每側設置5 道環肋時，鋼筋錨固長度達8d 的接頭模型殘余變形＜0.1 mm。

3.4 鋼筋錨固長度對接頭性能的影響

3.4.1 強度

鋼筋錨固長度是影響連接接頭承載力以及黏結強度的重要因素。 基于所建立的數值模型，不斷調整加載時長，分別得到套筒每側3、4、5 道環肋的接頭在不同鋼筋錨固長度發生破壞時的荷載；接頭承載力以及黏結強度與鋼筋錨固長度的關系曲線如圖17 所示，鋼筋黏結強度的計算由式(2)表示為

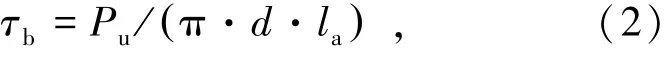
式中τb為鋼筋黏結強度，MPa； Pu為接頭承載力，kN，d 為鋼筋公稱直徑，mm； la為鋼筋錨固長度，mm。

由圖17 可知，鋼筋錨固長度越大，接頭的承載力越高，但黏結強度越低。 鋼筋錨固長度由5d 增加到6d，3 條曲線斜率近似，說明錨固長度對提高接頭承載力及降低黏結強度的影響程度與套筒一側設置幾道環肋關聯較少；鋼筋錨固長度由6d 增加到7d，接頭承載力提高最多的是套筒每側設置5 道環肋的接頭；鋼筋錨固長度由7d 增加到8d，套筒每側設置4 道環肋的接頭承載力曲線斜率明顯增大，黏結強度曲線斜率明顯減小；鋼筋錨固長度由8d 增加到9d，套筒一側5 道環肋的接頭比一側4 道環肋的接頭承載力多增加了1%，因此僅從提高接頭承載力的角度考慮，套筒一側設置4 道環肋時，8 倍鋼筋直徑是最優的鋼筋錨固長度。

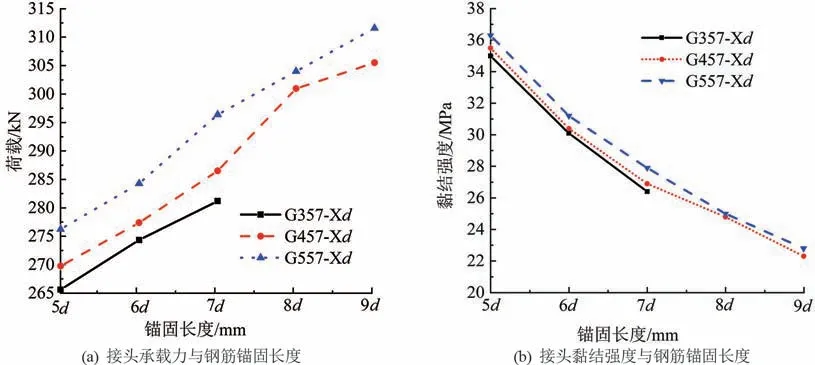
圖17 接頭承載力及黏結強度與鋼筋錨固長度的關系曲線圖

綜上所述，套筒一側環肋數量不少于3 道、鋼筋錨固長度不小于5 倍鋼筋直徑時，鋼筋錨固長度的增加對接頭承載力的提高以及黏結強度的降低效果不明顯。 鋼筋錨固長度越長，說明鋼筋與灌漿料的接觸面積越大，機械咬合作用越強，因此接頭承載力與鋼筋錨固長度曲線呈正相關走勢。 鋼筋黏結應力與鋼筋錨固長度呈負相關，原因在于鋼筋錨固長度越長，鋼筋的黏結應力分布越不均勻[14]。

3.4.2 變形

圖18 為鋼筋屈服前，不同鋼筋錨固長度接頭構件的荷載-位移曲線。 曲線斜率與鋼筋錨固長度成正比，即接頭變形越小，每種環肋數量的接頭構件的變形比較接近。 接頭殘余變形數值模擬結果見表5。

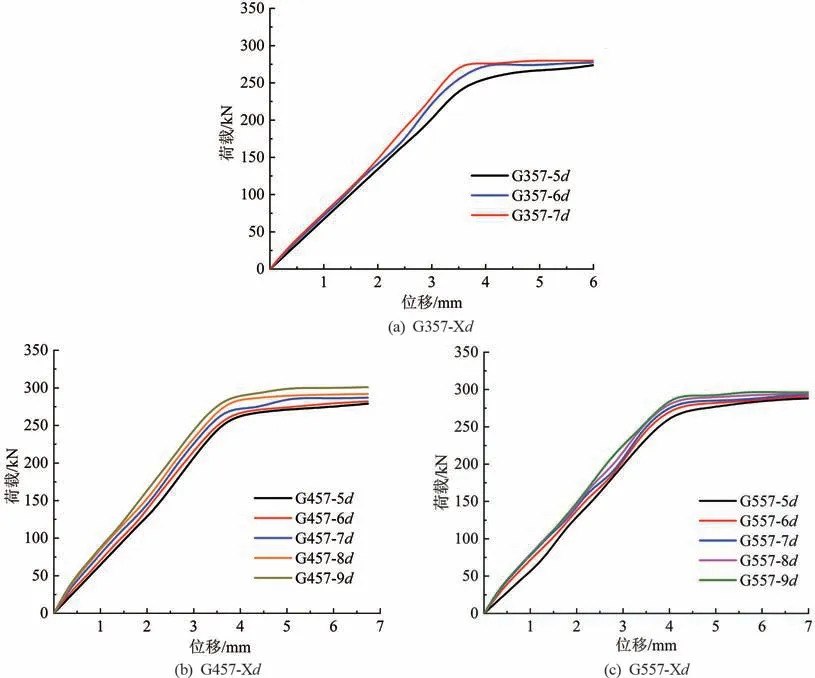
圖18 不同錨固長度接頭的荷載-位移曲線圖

3.5 鋼筋套筒灌漿連接接頭數值模擬

根據T/CECS 687—2020《鋼管滾壓成型灌漿套筒鋼筋連接技術規程》[18]以及市面套筒規格，對直徑為18、25 mm 的600 MPa 鋼筋建立相應的數值模型。 直徑為18 mm 的鋼筋采用外徑為48 mm、壁厚為3.5 mm 的GDPS 套筒；直徑為25 mm 的鋼筋選用外徑為 60 mm、壁厚為 5.5 mm 的 GDPS 套筒[19]。模型G348-18-6d、模型G560-25-8d 以及鋼筋、灌漿料、套筒的軸向應力云圖如圖19、20 所示。

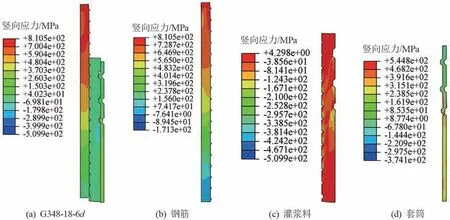
圖19 G348-18-6d 軸向應力云圖

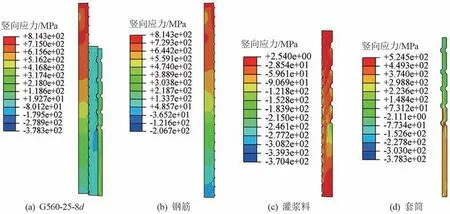
圖20 G560-25-8d 軸向應力云圖

由圖19、20 可知，鋼筋主要承受軸向拉力，從頂端到底部逐漸減小，直徑為18 和25 mm 的鋼筋對應的最大拉應力分別為810、814 MPa，均沒有超過845 MPa 的抗拉強度；灌漿料在鋼筋環肋上側與套筒凸肋下側產生壓應力，其他位置產生拉應力；套筒整體受拉，在靠近灌漿料一側3 個凸肋主要受壓，且在第一道肋(靠近套筒中部)處拉應力最大。 通過數值模擬得到的接頭承載力與殘余變形值見表6。

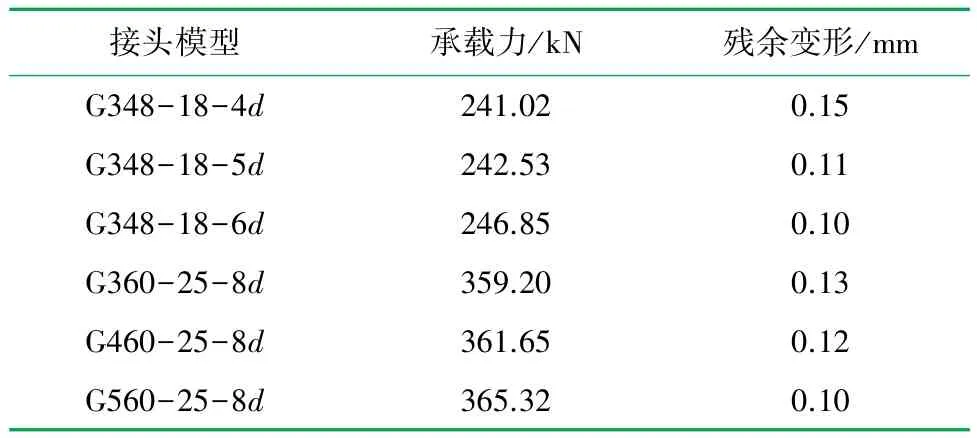
表6 鋼筋套筒灌漿連接接頭數值模擬結果表

由表6 可知，為了滿足接頭承載力與殘余變形的要求，對于直徑為18 mm 的鋼筋，套筒每側可設置3 道環肋，對于直徑為25 mm 的鋼筋，套筒需每側設置5 道環肋。

3.6 套筒規格

綜合考慮接頭構件的強度與變形兩個性能指標，套筒環肋數量與鋼筋錨固長度應對應設計，直徑為 18、22、25 mm 的 600 MPa 鋼筋所對應的套筒規格見表7。

表7 套筒規格表

4 結論

通過對600 MPa 鋼筋、高強水泥基灌漿料以及Q390 無縫鋼管滾壓制成的套筒灌漿連接接頭進行單向拉伸試驗與有限元數值模擬，主要得到以下結論:

(1) 套筒無環肋段的灌漿料位移隨環肋數量的增加而減小，環肋間灌漿料的滑移套筒受數量環肋影響較小。 光滑段的套筒表面軸向應變均為拉應變，環肋間既有拉應變也有壓應變，應變值遠小于光滑段；套筒表面環向應變均為壓應變，光滑段環向應變絕對值小于同位置的軸向應變。

(2) 鋼筋錨固長度達到8d 后，接頭承載力與變形受套筒環肋數量的影響減小。 對于直徑為18 mm的鋼筋，可選用Φ48×3.5 的鋼套筒，每側環肋數量不少于3 道；對于直徑為22 mm 的600 MPa 鋼筋，可選用 Φ57×5 的鋼套筒，每側環肋數量不少于4 道；對于直徑為25 mm 的鋼筋，可選用Φ60×5.5的鋼套筒，每側環肋數量不少于5 道。