基于QHAdam梯度優化算法的最小二乘逆時偏移

王紹文， 宋鵬,2,3*， 譚軍,2,3， 解闖， 趙波,2,3， 毛士博

1 中國海洋大學海洋地球科學學院， 青島 266100 2 青島海洋科學與技術試點國家實驗室， 海洋礦產資源評價與探測技術功能實驗室， 青島 266100 3 中國海洋大學海底科學與探測技術教育部重點實驗室， 青島 266100

0 引言

最小二乘逆時偏移(Least-Squares Reverse Time Migration, LSRTM)首先由Dai等(2010, 2011)提出，其是一種基于最小二乘反演框架下的高精度成像方法.相對逆時偏移而言，LSRTM可以有效壓制成像剖面中的低頻噪聲，成像結果趨于實際地層反射系數，因此近年來，LSRTM一直是地球物理領域的研究熱點.

經過10余年的發展，LSRTM得到長足的進步.Yao和Yakubowicz(2012, 2016)實現了基于矩陣的LSRTM和非線性的LSRTM，通過實驗證明了其有效性.Dong等(2012)以及郭振波和李振春(2014)通過實驗證明了LSRTM是一種真振幅成像方法，其成像結果具有明確的物理意義.Zhang等(2013b)建立互相關目標泛函，通過相位進行匹配，得到了穩定的LSRTM.Zhang等(2013a)、黃建平等(2014)將LSRTM應用于地表復雜的模型當中，得到了高精度的成像結果.李振春等(2014)將黏聲介質的成像引入到LSRTM當中，避免了反Q偏移方法存在的不穩定問題，驗證了其相較于常規LSRTM而言更加符合實際情況，具有更高的保幅性.Tan和Huang(2014)將計算得到的成像結果反推至背景速度模型中，不斷更新背景速度模型，提高了LSRTM對背景速度模型的穩定性.劉玉金和李振春(2015)提出了擴展成像條件下的LSRTM方法，其能夠在速度模型不準確的情況下獲得更高的成像分辨率.劉學建和劉伊克(2016)發展了基于多次波的LSRTM成像方法，獲得了更好的地下照明和覆蓋效果.李慶洋等(2017)考慮到實際情況中子波空變的特征，為了避免子波的影響及降低地震數據噪聲對LSRTM的影響，將Student′s t分布推廣到不依賴子波的LSRTM中.Yang等(2019)利用多階Born近似，補充線性化正演中缺失的振幅信息，降低了LSRTM的敏感程度，增強了垂直構造的成像結果.方修政等(2018)通過逆散射成像條件對梯度進行預處理，提升了LSRTM收斂效率和成像精度.黃金強和李振春(2019)發展了TTI介質中純qP波疊前平面波LSRTM成像方法，有效提升了反演成像的效率和反演算法的魯棒性，同時降低了LSRTM對模型參數的依賴性.郭旭等(2019)研究了基于一階速度-應力方程的VTI介質LSRTM方法，并對速度等參數對成像結果的敏感性做出了細致的分析.鞏向博等(2019)將稀疏約束引入LSRTM中，提升了小尺度散射體的成像精度.Mu等(2021)利用分離的繞射波進行LSRTM，對斷層-巖溶地區進行了高精度成像，為此地區的高精度解釋建立了基礎.周東紅等(2020)提出了適用于起伏地表的差分網格，并將其應用于LSRTM中，有效壓制了成像的部分串擾噪聲.劉玉敏等(2021)發展了基于衰減補償的黏彈性波LSRTM方法，其相較于彈性波LSRTM具有更快的收斂速度和更高的成像精度.王曉毅等(2021)利用Poynting矢量對梯度算子進行改造，得到了成像噪聲更小、收斂速率更快的LSRTM算法.胡勇等(2021)利用LSRTM在時頻域實現了對深部構造的高精度成像.

當前的LSRTM通常采用梯度類算法迭代求解，往往需要幾十次甚至上百次的迭代處理，其在整個迭代反演流程中尚存在如下問題：首先，當前采用的各種梯度求解算法，如共軛梯度(Polyak, 1969)、L-BFGS(Liu and Nocedal, 1989; Nocedal and Wright, 2006)以及截斷牛頓算法(Nash, 2000)等，由其所求的梯度并沒有得到優化，導致收斂效率和成像精度不高；此外，梯度類算法在每次模型更新時都需計算一個迭代步長，須付出1～2次波場延拓計算的代價，進一步降低了LSRTM的計算效率.

隨著計算機技術的進步，近幾年以卷積神經網絡(Hinton and Salakhutdinov, 2006)、U型網絡(Ronneberger et al., 2015)等為代表的深度學習技術發展迅猛.深度神經網絡的學習過程本質上也是一個基于梯度的反演優化問題，以卷積神經網絡為例，其每個卷積層都有若干個待求卷積核，而整個網絡通常含有上百萬、千萬個待優化參數，因此神經網絡的訓練過程中都要應用RMSProp(Hinton et al., 2012)、Adam(Kingma and Ba, 2017)以及QHAdam算法(Ma and Yarats, 2019)等先進的梯度優化算法對反傳梯度進行優化，以提高各卷積層參數反演的收斂效率.近年來，已有部分學者嘗試將各種梯度優化算法引入地球物理領域，以解決反演優化問題.Wu等(2018)將Adam算法應用于頻率域LSRTM中，結果顯示相比于梯度下降算法，Adam算法的成像精度更高.Bernal-Romero和Iturrarán-Viveros(2020)將七種自適應學習率算法引入到傳統時間域全波形反演算法中，結果顯示與傳統算法相比這些算法不但具有計算效率優勢，同時具有收斂效率和反演精度優勢.

本文將深度學習中的QHAdam算法(Ma and Yarats, 2019)引入到時間域LSRTM中，可在付出極小計算代價的前提下，直接獲得優化的模型更新量，可顯著提升LSRTM收斂效率和成像精度，同時還可避免每次迭代時迭代步長的計算，從而在一定程度上提升LSRTM的計算效率.

1 LSRTM原理及實現流程

常密度聲波方程可表示為：

(1)

其中，c0為背景速度場，p0為與位于xs的震源f相關的壓力場.

對背景速度施加一擾動δc，則產生的波場為p=p0+δp，其中δp為擾動波場，波場p滿足方程：

(2)

其中c=c0+δc,p為與位于xs的震源f相關的壓力場.

將速度項泰勒展開為：

(3)

將式(2)與(1)相減可得擾動波場δp為：

(4)

定義刻畫偏移速度與真實速度偏離程度的擾動模型(或真實反射率)為m(x)=2δc(x)/c0(x)，則式(4)可寫為：

(5)

記錄檢波點位置xr上的波場值δp(xr;t;xs)即得到Born近似的模擬數據dsyn(t,xr).LSRTM即基于公式(5)，通過梯度下降類算法迭代優化m來不斷縮小預測數據dsyn與觀測數據dobs在最小二乘意義下的誤差.

根據伴隨狀態法可得到LSRTM中梯度計算公式為(Plessix, 2006)：

(6)

其中，伴隨波場q滿足：

(7)

為提升LSRTM的收斂效率，通常需將梯度轉換成共軛梯度，然后應用基于梯度預處理算法 (Zhang et al., 2012, 2011)、L-BFGS算法(Yang and Zhang, 2018)或截斷牛頓算法(王義和董良國, 2015)等實現迭代反演.然而，無論采取何種梯度算法，常規LSRTM得到的梯度均未進行梯度優化處理，其會導致整個LSRTM的收斂效率和收斂精度不高；此外，每次迭代時，為得到模型更新量，一般還需付出1～2次波場延拓計算來求取迭代步長，這進一步降低了LSRTM的計算效率(常規LSRTM處理流程見圖1).

圖1 常規LSRTM實現流程Fig.1 Flow chart of LSRTM with conventional algorithms

2 基于QHAdam梯度優化算法的LSRTM

梯度優化算法在深度學習領域應用廣泛.深度神經網絡通常含有上百萬、千萬個待優化參數，因此神經網絡的訓練過程中都要應用RMSProp(Hinton et al., 2012)、Adam(Kingma and Ba, 2017)等先進的梯度優化算法對反傳梯度進行優化，以提高各層參數反演的收斂效率.而其中Adam算法是深度學習領域中常用的梯度優化算法，目前已有部分學者嘗試將Adam算法引入全波形反演(Bernal-and Iturrarán-Viveros, 2020)或最小二乘逆時偏移領域(Vamaraju et al., 2021; Wu et al., 2018)，顯著提高了收斂效率和計算精度.

Adam算法利用了梯度的一階和二階矩估計為不同參數提供自適應的步長，第k次迭代梯度的有偏一階矩估計sk計算了前k-1(k>0)次迭代梯度的指數加權：

sk=β1sk-1+(1-β1)gk,(8)

其修正項可表示為：

(9)

第k次迭代的梯度的有偏二階原點矩估計rk計算了前k-1次迭代梯度平方的指數加權：

rk=β2rk-1+(1-β2)gk⊙gk,(10)

其修正項可表示為：

(11)

Adolphs等(2020)證明了可以將Adam類算法視為橢球約束的一階信賴域方法，可使用歷史梯度的指數加權平均來對當前梯度進行縮放，使其步長能夠自適應優化過程，Adam算法模型更新量可表示為(Kingma and Ba, 2017)：

(12)

其中，mk和mk-1分別表示第k和k-1次迭代的模型參數(LSRTM中為真實反射率)，s0=r0=0，β1和β2為常數，在深度學習中一般設置為0.9和0.999，α為初始迭代步長，ε為保持數值穩定的常數，一般為10-8.基于公式(12)，Wu等(2018)實現了頻率域的LSRTM.

然而對于Adam算法，如果某些參數的梯度接近于零，會使公式(12)第二項的分母遠小于分子，此時更新量會出現異常值，導致優化過程不穩定.為解決此問題，Ma和Yarats(2019)通過大量實驗證明了時間不一致性在隨機優化器中的重要性，因此他們將Adam算法中的具有時間一致性的指數貼現函數(見公式(13))替換為不具有時間一致性的擬雙曲貼現函數(公式(14))，由此形成了QHAdam算法，該算法可以通過設置超參數v來避免Adam算法可能會出現的不穩定問題，獲得更加穩定的收斂.公式(13)和(14)為：

dEXP,β(k)=(1-β)βk,(13)

(14)

式中，v和β均為常數.

將Adam算法中的矩估計項替換為擬雙曲項即可得到基于QHAdam算法的模型更新量計算公式(Ma and Yarats, 2019)：

(15)

(16)

(17)

v1、v2、β1、β2以及α等參數的選取對于算法的穩定性和收斂效率均有一定的影響，本文大量實驗測試結果表明，當β1=0.7、β2=0.999、v1=0.999、v2=1.0時QHAdam算法具有較優的收斂效率和穩定性；而對于初始步長α，本文采用如下所述的初始步長設置策略：在第一次模型更新迭代時，利用傳統算法計算模型更新量，并將其絕對值的最大值的0.5倍(公式(18))設置為初始步長，并在隨后的迭代中對初始步長施加衰減系數γ=0.99的指數衰減.公式(18)為：

αk=max{|Δm0|}/2*γk-1.

(18)

圖2 基于QHAdam優化算法的LSRTM實現流程Fig.2 Flow chart of LSRTM with QHAdam algorithm

基于QHAdam算法LSRTM流程圖如圖2所示.對比圖1和圖2可知， 基于QHAdam算法的LSRTM除需第一次迭代外，后續迭代中均應用公式(15)和(18)計算優化的模型更新量，不需計算迭代步長，因此與傳統算法相比，該方法具有更高的計算效率.另外，由于Adam算法和QHAdam算法分別使用梯度平方的指數貼現和擬雙曲貼現來對梯度項進行縮放，能夠為空間不同點的梯度提供自適應的步長，因此無需對梯度進行照明補償，能夠由梯度gk直接求取優化后的模型更新量Δmk.

3 Marmousi模型實驗

本文使用的Marmousi模型深度為3.5 km(其中固定水深0.5 km)，寬度為9.2 km(真實速度模型如圖3a所示).實驗采用主頻為10 Hz，時間采樣間隔為1 ms的雷克子波作為震源，共模擬460炮地震記錄作為實測地震記錄.每炮地震記錄共460道，記錄長度為4 s，炮間距設為20 m，道間隔也為20 m，炮點和檢波點均放置于模型表面.成像使用的偏移速度如圖3b所示，真實反射率如圖3c所示.

本文分別基于L-BFGS算法、Adam算法以及QHAdam算法應用Marmousi模型進行LSRTM成像實驗，第30次迭代成像結果如圖4所示，切片對比結果如圖5所示.其中L-BFGS算法存儲了10次迭代信息用于重建Hessian矩陣且未使用照明補償，Adam算法中β1=0.9，β2=0.999，ε=10-8；QHAdam算法中β1=0.7，β2=0.999，v1=0.999，v2=1.0，ε=10-8.

圖3 Marmousi模型(a) 真實速度； (b) 偏移速度； (c) 真實反射率.Fig.3 Marmousi model(a) True velocity model; (b) Migration velocity model; (c) True reflectivity.

由圖4可知，基于Adam算法和QHAdam梯度優化算法的LSRTM成像結果精度明顯優于L-BFGS算法反演結果，尤其在中深層其成像精度優勢更為明顯.圖4中4.6 km和6.2 km處單道成像結果對比見圖5a、b，其中黑色曲線為真實反射率，綠色曲線為基于L-BFGS算法的成像結果，藍色曲線為基于Adam梯度優化算法的成像結果，紅色曲線為基于QHAdam梯度優化算法的成像結果.由圖5可知，基于L-BFGS算法的LSRTM其成像精度最低，而基于QHAdam梯度優化算法的LSRTM具有最高的成像精度，其更接近于真實反射率模型.

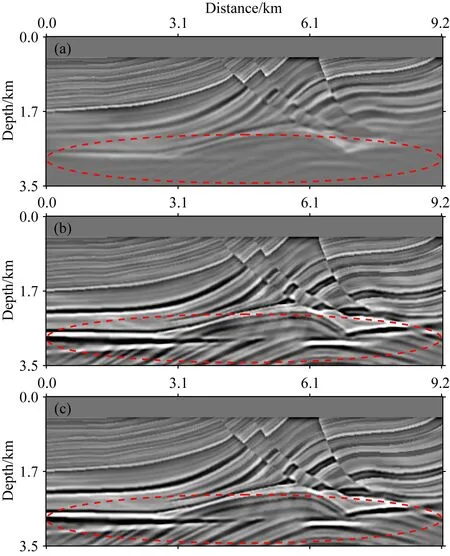
圖4 基于不同優化算法的LSRTM結果(a) L-BFGS； (b) Adam； (c) QHAdam.Fig.4 LSRTM results

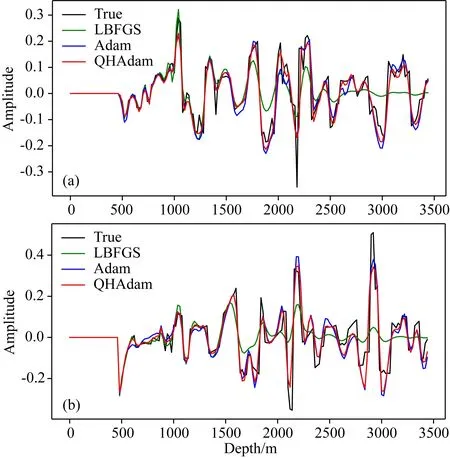
圖5 基于不同算法的成像單道切片結果(a) Marmousi模型4.6 km處； (b) Marmousi模型6.2 km處.Fig.5 Single trace contrast based on different algorithm(a) Comparison of vertical amplitude at 4.6 km; (b) Comparison of vertical amplitude at 6.2 km.

為全面評估三種算法成像結果的精度，本文應用公式(19)來評估成像結果和真實反射系數的誤差：

(19)

其中，mresult表示最終成像結果，mreal代表真實反射率.三種算法的成像精度評估因子迭代曲線見圖6.由圖6可知，相比于L-BFGS和Adam算法，基于QHAdam梯度優化算法的LSRTM具有更高的收斂效率.

圖6 成像誤差迭代曲線Fig.6 Imaging error curves

圖7為對目標函數對數隨迭代次數變化曲線，由圖7可知，QHAdam算法收斂效率最高.同時我們也注意到，前7次迭代中L-BFGS的目標函數收斂要優于QHAdam算法(如圖7所示)，并且直到30次迭代結束，L-BFGS算法也要優于Adam算法，這主要是由于L-BFGS算法更適應于淺層的收斂成像，Adam算法和QHAdam算法注重于全局的優化成像，而由于幾何擴散的影響，導致L-BFGS算法的目標函數整體優于Adam算法，前7次優于QHAdam算法.但是事實上由圖6模型誤差曲線可知，Adam算法要優于L-BFGS算法，并且無論從模型誤差還是目標函數來看，QHAdam算法的收斂效率均優于L-BFGS算法和Adam算法.

圖7 目標函數對數迭代曲線Fig.7 Logarithms objective function curves

本文基于兩張Telsa-V100卡執行基于三種不同算法的LSRTM，三種算法各30次迭代計算時間如表1所示.

表1 不同梯度算法LSRTM迭代時間Table 1 Computation time of different algorithms

由表1可知，基于Adam算法和QHAdam類梯度優化算法的LSRTM其計算效率要高于常規LSRTM成像算法，這是其不需要計算梯度步長而節省的1次波場延拓計算時間所致.

4 結論

本文將深度學習中的QHAdam算法引入到傳統LSRTM計算中實現了模型修改量的優化處理，其在付出極小計算代價的前提下，直接獲得優化的模型更新量，避免了計算步長的求取.Marmousi模型實驗結果顯示，相比于常規LSRTM算法，基于QHAdam梯度優化算法的LSRTM其收斂效率和反演精度更高，且由于減少了迭代步長的求取步驟，其也具有更高的計算效率；同時相對于基于Adam算法的LSRTM，基于QHAdam梯度優化算法的LSRTM也具有更高的收斂效率和收斂精度.

致謝感謝中國海洋大學地球探測軟件技術研發團隊提供的資助和支持，感謝審稿專家提供的寶貴意見.