中國大陸強震的早期余震概率預測效能評估與制約因素

畢金孟, 蔣長勝, 來貴娟, 宋程

1 天津市地震局， 天津 300201 2 中國地震局地球物理研究所, 北京 100081

0 引言

強震發生后隨時發生的強余震嚴重威脅震區的經濟社會和人民生命財產安全，及時發布權威可靠的強余震預測信息，對抗震救災、應急管理決策以及災后恢復重建等工作意義重大(Reasenberg and Jones, 1989; Marzocchi and Lombardi, 2009; Woessner et al., 2011; Nanjo et al., 2012; Ogata et al., 2013).強余震發生的時間跨度可從幾秒到幾年，但大多數的余震是在主震過后數天內發生的(JMA, 2009).主震過后已受損的建筑物來不及修復的情況下便再次遭受余震的繼續作用，產生累計損傷效應、造成更為嚴重的人員傷亡和財產損失.例如2010年9月3日的新西蘭7.1級地震之后的6.3級強余震造成了146人死亡、300多人失蹤及建筑物的破壞(張晁軍等, 2011)，1976年唐山7.8級大地震之后的灤縣7.1級強余震、寧河6.9級強余震造成余震區域的房屋幾乎全部倒塌及橋面鐵路損毀等(呂曉健等, 2007)，2003年日本北海道8.0級地震之后的5.0級強余震造成了儲油罐溢出引發火災的次生災害(趙金寶, 2005)，以及其他在余震作用下造成的人員財產損失和建構筑物的破壞.關于強余震造成的累計震害損失問題已在巨災保險的災害模型構建中引起高度關注(熊政輝, 2019).因此，作為地震預測中“可操作性”較強并可能取得明顯減災實效的早期強余震概率預測，尤其是震后3天內的強余震概率研究工作，將更為有效的提升防震減災和公共服務水平.

對強余震的預測建模和效能評估始終是地震減災領域的熱點科學問題.例如Sornette等(1996)從物理學引入級序分析(rank-ordering analysis)方法用于預測余震序列中的最大事件，在統計地震學上基于G-R關系的b值截距法(吳開統等, 1984)和最大余震震級法(Shcherbakov and Turcotte, 2004)，以及進行概率預測的R-J模型(Reasenberg and Jones, 1989)和ETAS模型(Ogata, 1989)都在國內外得到廣泛應用.Steacy等(2014)從物理模型與統計模型相結合的角度，將 Coulomb 模型和 STEP 模型結合研究了Canterbury 地震序列的余震發育情況.從聚焦到震后早期的強余震預測角度，Shcherbakov等(2018)利用地震序列中的早期事件(前震或早期余震)以及震級-頻度分布和地震發生率分布，構建了極端事件震級大小的貝葉斯預測分布，可用于考慮不確定度情況下的主震或強余震的震級預測.Gentili和Di Giovambattista(2017, 2020)利用震后早期余震次數和初期幾小時/幾天輻射能量時空演變的統計特征發展起來的一種模式識別技術對意大利東北部和斯洛文尼亞西部的破壞性之后的強余震進行了預測，成功地檢驗了1976年的高破壞性震群以及2019年的三個小震群.目前國際上正在進行的全球“地震可預測性合作研究”(Collaboratory for the Study of Earthquake Predictability, CSEP)計劃中，短期余震概率預測模型也得到快速發展(Schorlemmer et al., 2018).美國地質調查局(USGS)和全球地震模型(GEM)項目開展的“可操作的余震預測”(Operational Aftershock Forecasting，OAF)(Helmstetter et al., 2006; Console et al., 2010)也對規范震后早期強余震預測提供了重要的科學參考.

我國大陸地區地震強度大、頻度高，當前正處于人口和財富(GPD)向大城市和城市群快速集中過程中，防范化解包括大震巨災在內的重大風險是經濟社會發展的重要保障條件，切實提升強余震的預測能力和風險處置決策的科學水平的需求強烈.但長期以來偏向于定性的強余震預測，難于滿足震后地震災區現場應急救援、疏散和災后恢復重建，以及巨災保險保障等客觀需求.針對上述問題，本文選用當前國際上較為前沿的、可充分利用不完整地震記錄技術優勢的Omi-R-J模型(Omi et al., 2013, 2015, 2016)，對我國大陸地區強震開展早期余震的概率預測并量化評價預測效能，獲得的余震預測模型的適用性、預測限度和制約因素，為今后開展“可操作”的強余震預測提供參考，服務于實際的地震防災救災工作.

1 研究所用方法和資料

Reasenberg和Jones(1989)以余震衰減關系的Omori-Utsu公式(Omori, 1894; Utsu, 1961)作為頻次約束，以震級頻度分布的G-R關系(Gutenberg and Richter, 1944)作為強度約束的基礎上發展了余震短期概率預測的Reseanberg-Jones(R-J)模型.根據R-J模型，在地震序列中t時刻震級不低于M的余震強度函數可表示為：

(1)

式中的t為主震發生后的時刻，一般取正值.參數k控制余震活躍程度，在很大程度上取決于單個余震序列，與主震震級關系不大.參數p表示地震序列的衰減程度，p值的大小與序列的衰減快慢呈正相關關系.參數c用于調節主震發生后極短時間內余震記錄的不完整性，是一個數值極小的正常數，與震源深度成負相關關系(Shebalin and Narteau, 2017).參數b表示了應力累積水平、大小上呈反比關系(Wiemer and Katsumata, 1999; Enescu et al., 2011).

Omi等(2013)在R-J模型的基礎上，將地震序列早期階段完整性震級以下的余震考慮到模型參數擬合和余震發生率預測中，提出了一種新的方法，簡稱為“Omi-R-J”模型.Omi等(2013)利用Ogata和Katsura(1993)給出的檢測率函數q(M)的表達方式(OK1993模型)，來對地震事件記錄不完整部分的檢測程度進行描述.而實際記錄到的地震概率密度函數可表示為：

=βe-β(M-μ)+β2σ2/2q(M|μ,σ),(2)

式中的β為bln10，μ表示檢測率為50%時對應的震級、σ為相應的震級離散度，通常用μ+2σ或者μ+3σ來近似最小完整性震級Mc.余震記錄的檢測率會隨時間動態變化，在地震序列早期階段由于大量余震事件缺失、往往具有較高的μ值，此后逐步恢復至正常水平.

在對公式(2)的參數估計中，采用了Omi等(2013)發展的“狀態-空間”模型(Omi et al., 2013)來估計隨時間變化的μ(t).具體思路為，設定μ(t)為余震發震時刻序列ti≤t≤ti+1(i=1,2,…,n)對應離散的分布函數，假設一個對μ(t)平滑約束的先驗分布并設定超參數V來控制其平滑程度，利用最大期望(EM)的迭代算法對參數β、σ、V進行優化和最大后驗估計后，通過貝葉斯估計來獲得參數μ=(μ1,μ2,…,μn)T.此后進一步結合Omori-Utsu公式和最大似然法來確定參數p，c，k及標準差.

根據參數估計結果，利用公式(1)即可計算在震級范圍M>Mp和任意時間間隔[t2,te]內的余震預測數目：

(3)

為對中國大陸強震的余震序列展開研究，使用了中國地震臺網中心提供的《全國統一正式編目》地震目錄(1)1)全國地震編目系統.http:∥10.5.160.18/console/exit.action.[2020-10-31]..篩選出225例6.0級及以上地震事件，使用Gardner-Knopoff方法(Gardner and Knopoff, 1974)對其中的叢集地震進行刪除，保留獨立的主震事件134例.采用畢金孟和蔣長勝(2019)給出基于緯度-時間圖、經度-時間圖以及震中分布圖相結合的“自然邊界法”來選取計算所用的地震序列目錄.為保證參數擬合的穩定性和質量，利用“震級-序號”法(蔣長勝和吳忠良, 2011)確定每個序列的最小完整性震級，保證完整性震級以上的地震數目不少于40個，由此共選取了86個地震序列開展相關的研究.相應的主震參數如表1所示，主震的震中空間分布如圖1所示.

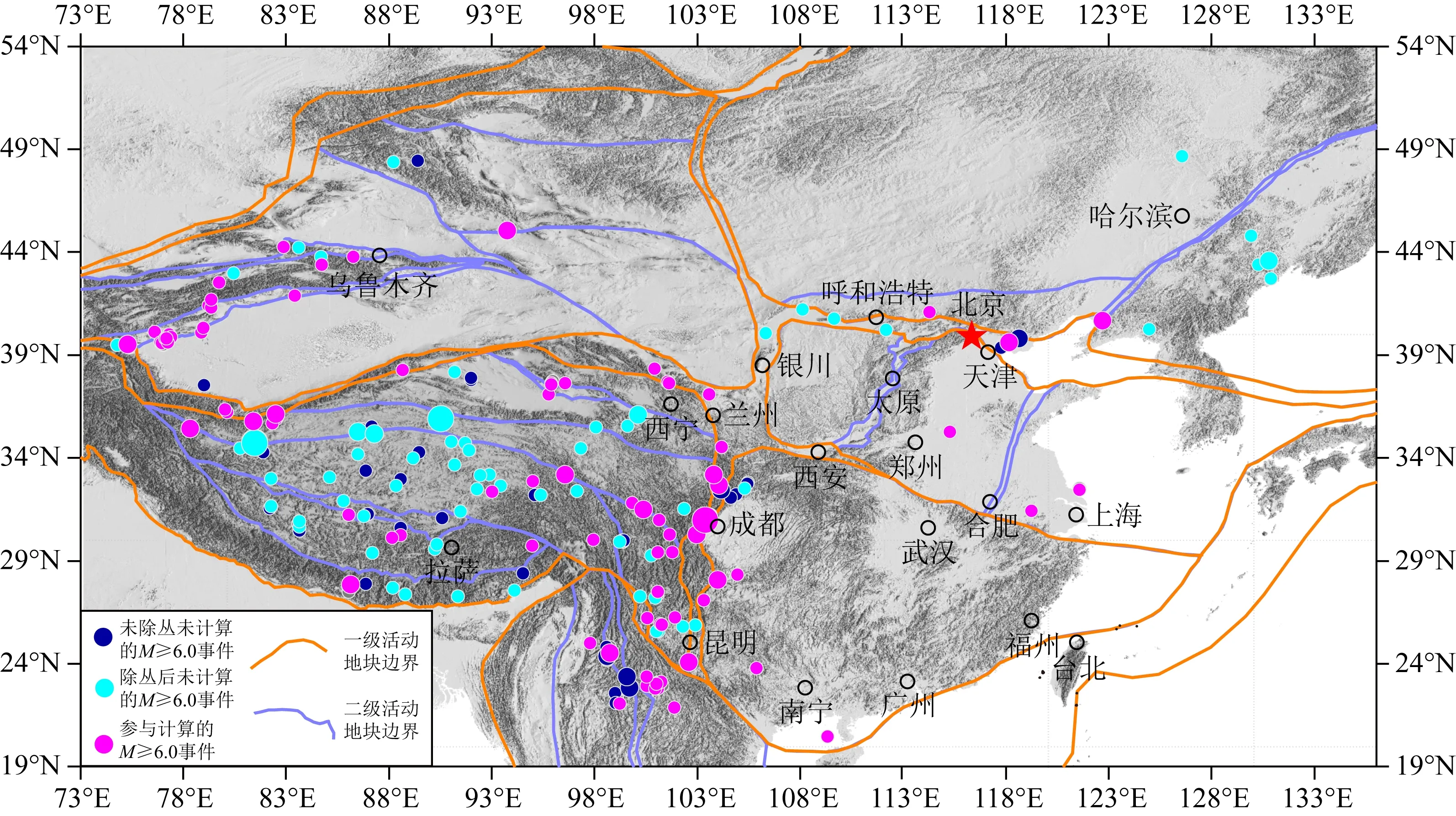
圖1 中國大陸1970年以來6.0級以上地震的空間分布Fig.1 Epicentre distribution of earthquakes (M≥6.0) since 1970 in continental China

Omi-R-J模型利用對每個地震事件逐步迭代的方式，可獲得研究時段內的地震檢測率隨時間的變化.圖2給出了2020年1月19日新疆伽師MS6.4地震序列按照Ogata和Katsura(1993)模型的50%地震檢測率μ(t)的分布，為考察擬合過程的穩定性，分別計算了主震發生后的0～0.05天、0～1.00天、0～2.00天、0～3.00天和0～30.00天，共計5個時段的檢測率分布情況.

圖2 2020年1月19日新疆伽師MS6.4地震序列的完整性分析圖中各顏色的曲線分別標出了不同時段(震后0～0.05天、0～1.00天、0～2.00天、0～3.00天和0～30.00天)所對應的50%地震檢測率的結果，灰色圓點代表了新疆伽師MS6.4地震事件的余震.Fig.2 Catalogue completeness analysis of the Xinjiang Jiashi MS6.4 earthquake sequence on January 19, 2020The colored curves indicate the results of the 50% detection rate calculated from data at different time periods (0～0.05 day, 0～1.00 day, 0～2.00 days, 0～3.00 days and 0～30.00 days) after the mainshock. The grey dots represent the aftershocks of Xinjiang Jiashi MS6.4 earthquake.

2 地震序列參數的擬合情況

震后快速獲得較為穩定的模型序列參數，是震后短時間內提升余震預測能力關鍵(蔣長勝等, 2017, 2018; 畢金孟和蔣長勝, 2017)，而震后早期小震波形的“淹沒”所導致的余震序列缺失，可能是影響模型參數穩定性的主要因素之一.震后早期階段余震大量缺失、傳統的嚴重依賴于完備性震級的ETAS、R-J模型難以給出準確的余震概率預測結果，而Omi-R-J模型充分利用了震后全部記錄的余震事件，并在震后短期內(0.05天)快速開展參數擬合，以2020年1月19日新疆伽師MS6.4地震序列為例，選取了0～0.05天、0～1.00天、0～3.00天、0～30.00天四個早期時間段進行了說明.震后早期序列持續時間t2=0.05天時的模型參數為β=1.733±0.292，k=0.011±0.075，p=1.020±0.140，c=0.016±0.065；序列持續時間t2=1.00天時的模型參數為β=1.729±0.106，k=0.023±0.011，p=0.899±0.119，c=0.094±0.049；序列持續時間t2=3.00天時的模型參數為β=1.859±0.083，k=0.012±0.006，p=0.853±0.0.072，c=0.071±0.037，序列持續時間t2=30.00天時的模型參數為β=1.853±0.054，k=0.015±0.005，p=1.024±0.0.033，c=0.192±0.047.

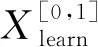
表1 中國大陸部分強震序列的Omi-R-J模型預測的N-test檢驗結果Table 1 A list of N-test parameters for some strong earthquake sequences in continental China based on the forecast results of Omi-R-J model

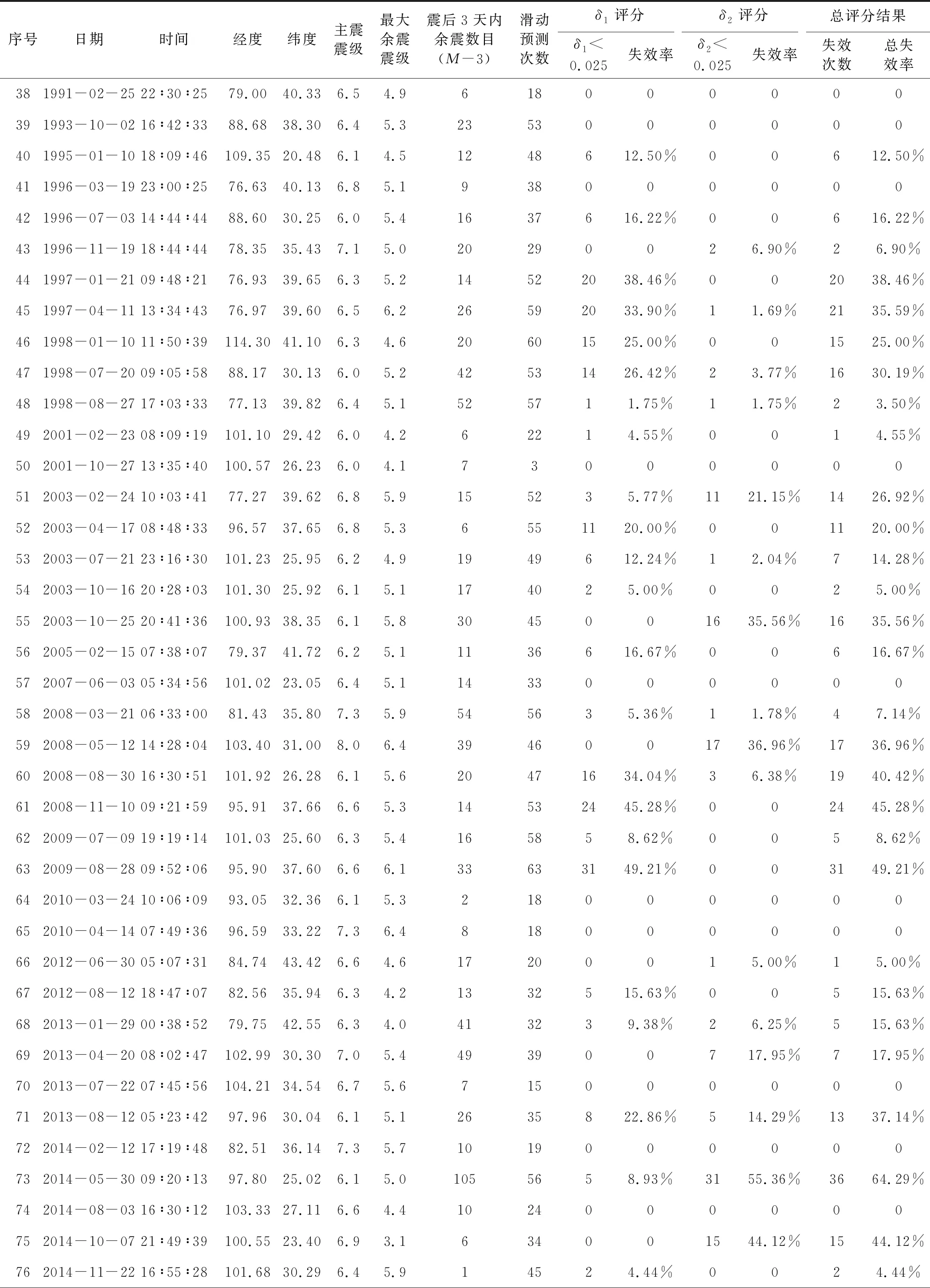
續表1

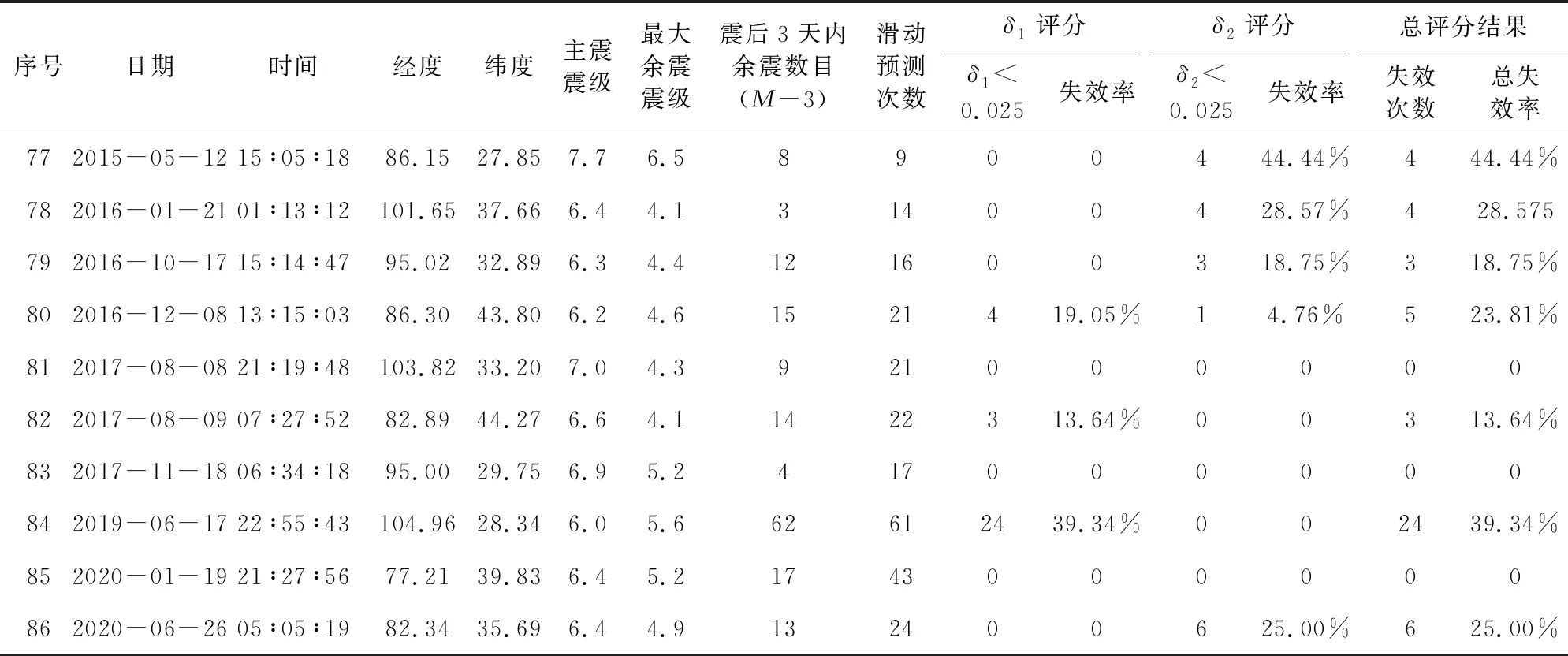
續表1

表2 中國大陸地區地震序列Omi-R-J模型參數擬合的整體統計特征Table 2 The overall statistical characteristics of the fitting parameters for the earthquake sequences in continental China based on the Omi-R-J model

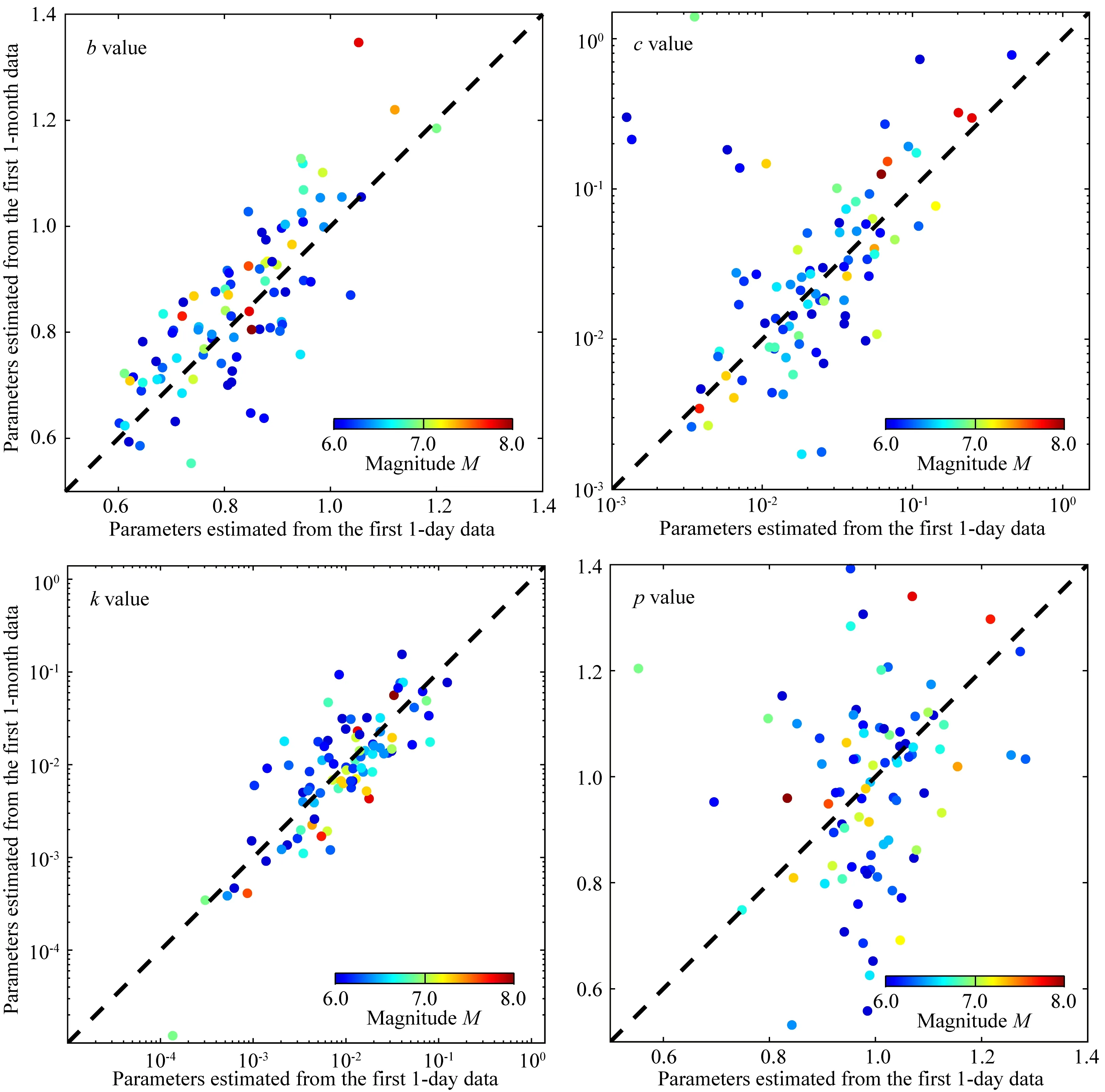
圖3 基于震后1天和30天數據的86個地震序列的Omi-R-J模型參數對比圖Fig.3 Comparison of aftershock sequence parameters estimated from the first 1-day span data against those from the first 30-days span data after the 86 mainshocks based on the Omi-R-J model

3 強余震概率預測效能評估

為更好的驗證Omi-R-J模型預測的地震數目與實際發生的地震數目的偏離程度，選用了CSEP計劃中針對地震數檢驗的N-test方法(Kagan and Jackson, 1995; Schorlemmer et al., 2007; Zechar, 2010)，并選用有效顯著性水平αeff=0.025來對N-test檢驗結果進行單邊檢驗，當δ1<αeff時，表示存在預測余震數目“過少”的情況；當δ2<αeff時則表明存在預測余震數目“過多”的情況.作為實例，圖4和圖5給出了Omi-R-J模型基于不同時間段的數據、不同時間尺度、不同震級檔分別在震級-頻次、時間-頻次上的對比結果，可以看出，分級分段分檔的實際發生地震數均在預測數的95%置信區間內，顯示了較好的預測效能.

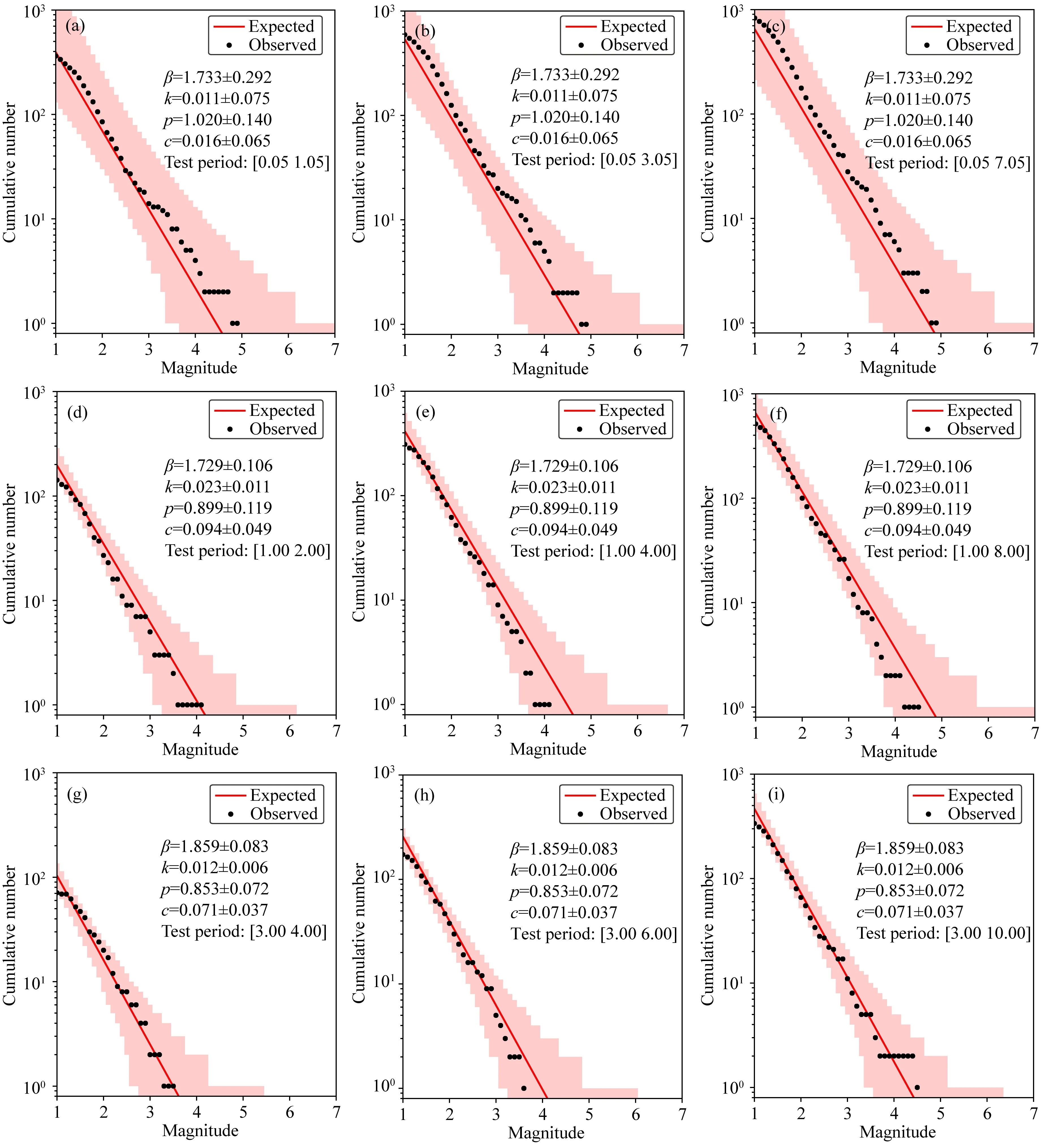
圖4 利用Omi-R-J模型對2020年1月19日新疆伽師MS6.4地震序列在震級-頻次上的強余震概率預測結果示例圖中分別是基于震后[0.05，1.00，3.00]天的數據預測未來1天(a、d和g)、3天(b、e和h)和7天(c、f和i)的強余震發生次數，其中黑色圓點為實際觀測結果，紅色線段為預測結果，粉色區域為預測結果的95%置信區間.Fig.4 Strong aftershock probability forecasting of magnitude-cumulative number of aftershocks result for the Xinjiang Jiashi MS6.4 earthquake sequence using the Omi-R-J model on January 19, 2020Based on the data of [0.05, 1.00, 3.00] days after the mainshock, the number of strong aftershocks in the next 1 day (a, d and g), 3 days (b, e and h) and 7 days (c, f and i), respectively. The black dots represent the actual observed aftershocks, the red lines represent the forecasting result, and the pink areas represent the 95% confidence interval of the forecasting result.

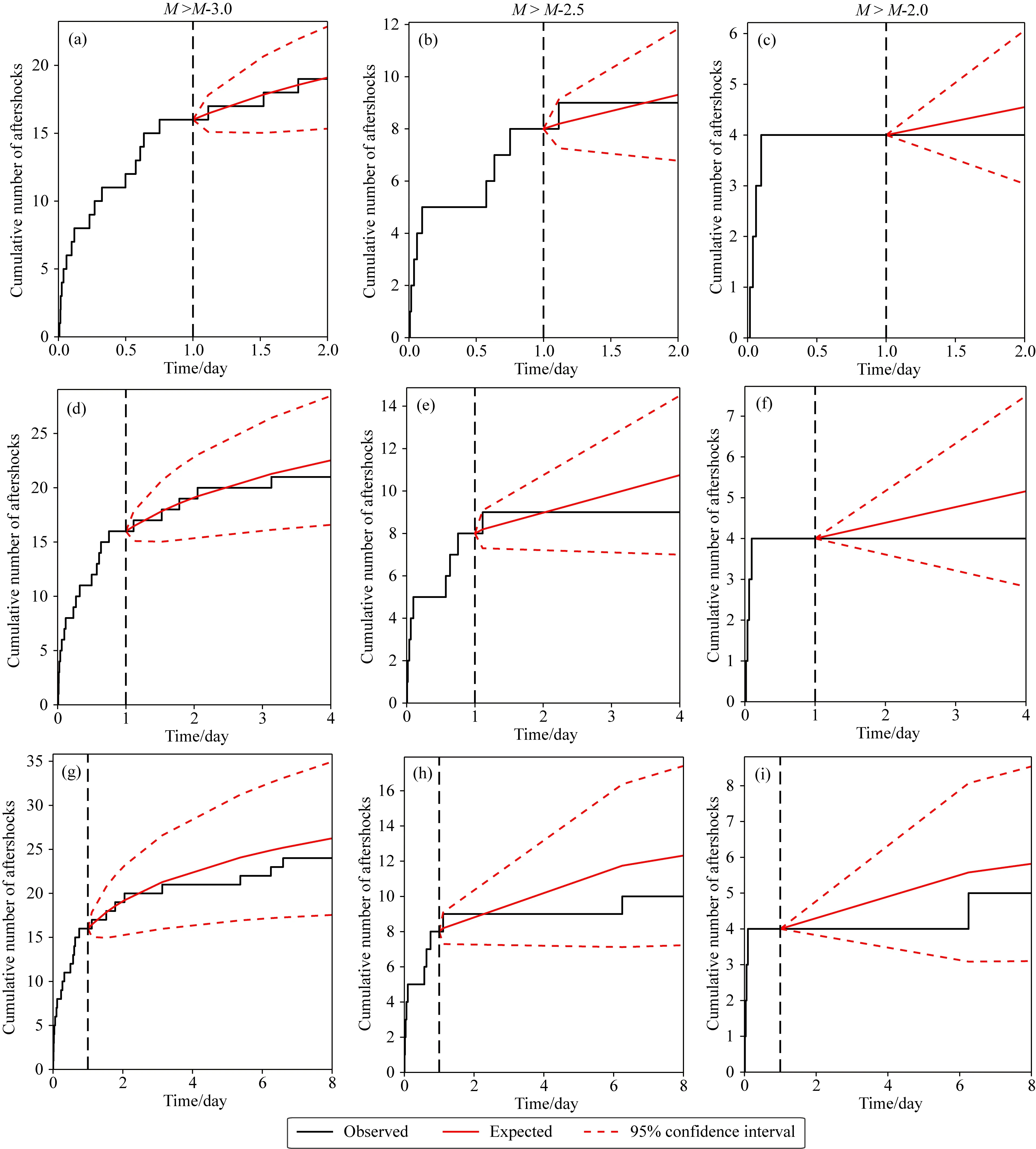
圖5 利用Omi-R-J模型對2020年1月19日新疆伽師MS6.4地震序列在時間-頻次上的強余震概率預測示例圖中分別是基于震后1天的數據預測未來1、3、7天在震級檔M-3.0(a、d和g)、M-2.5(b、e和h)和M-2.0(c、f和i)的強余震發生次數，其中黑色曲線為實際觀測結果，紅色曲線為預測結果，紅色虛線標出了預測結果的95%置信區間，黑色垂直虛線標出了預測起始時刻.Fig.5 Strong aftershock probability forecasting of time-cumulative number of aftershocks for the Xinjiang Jiashi MS6.4 earthquake sequence using the Omi-R-J model on January 19, 2020Based on the 1-day after earthquake, the number of strong aftershock forecasting with different magnitude M-3.0 (a, d and g), M-2.5 (b, e and h) and M-2.0 (c, f and i) in the next 1 day, 3 days, 7 days, respectively. The black curves represent the actual observation results, the red curves represent the forecasting results, the red dotted lines indicate the 95% confidence interval of the forecasting results,and the black vertical dotted lines indicate the forecasting start time.

為了對1970年以來中國大陸地震序列的早期余震(震后3.00天內)的預測效能進行系統性評估，因每個地震序列受到區域地震監測能力等因素的制約，Omi-R-J模型需要一定的地震數目才可以進行強余震預測，在0.05～3.00天的時間內盡可能的去“逼近”發震時刻，來進行分級分段分檔的概率預測，并對預測結果進行了“量化”的效能評估.因實際未發生地震不能進行N-test檢驗，為了更加客觀的進行評價，因此本文將預測有一定概率的地震發生，而實際沒發生地震的情況，并未考慮在統計范圍內.

面對復雜的地震序列，即使利用充分考慮小震事件的、公認的預測效果較好的Omi-R-J模型仍出現一些預測“失效”的情況.在所有參與計算的時間段內，其預測效能評估結果如圖6所示，從統計結果來看，預測過多占優的序列(39/86)大于預測過少占優的序列(19/86)；預測過少的比例大于預測過多的比例.從所有序列預測時段整體上來看，對于Omi-R-J模型，δ1<0.025的391次，即存在預測余震數目“過少”比例占12.14%；δ2<0.025的216次，即存在預測余震數目“過多”的比例占6.70%；總的預測失效的次數為607，預測失效的比例為18.84%，所有序列預測評估結果如表1所示.平均預測有效率指的是滿足不同條件下序列有效率的平均值，來探究不同情況下序列的整體預測效能.對所選單個序列總的平均預測有效率為83.82%；對所選序列1天、3天和7天的預測平均有效率分別為88.90%、82.76%、80.82%；對不同震級檔[M-3.0,M-2.5,M-2.0]預測的平均有效率為78.89%、86.14%、92.35%；基于震后早期不同時段([0.05, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0])預測的平均有效率為84.31%、92.06%、91.12%、90.74%、92.49%、91.87%、92.90%，具體整體的分級分段分檔結果如表3所示.由于預測次數的差異，整體的預測失效情況和單個序列預測平均失效結果存在稍小的差異.

4 討論

快速獲得震后較為穩定的序列參數，是提高強余震概率預測有效性的重要因素，Omi-R-J模型震后初期獲得的b、c、k值與穩定時段的序列參數具有較小的差異，這與利用匹配濾波技術拾取被常規地震臺網檢測遺漏的余震事件(Peng et al., 2006)、Zhuang等(2017)利用余震序列重新構建技術給出的地震序列參數穩定性所獲得的效果一致.為進一步討論震后早期預測失效的制約因素，統計了強震震級、序列參數和震后早期強余震數目(M-3)之間的關系，如圖7所示.由圖可知，震級的大小與震后早期的序列參數k、強余震數目(M-3)之間沒有明顯的相關性，而序列參數k與余震數目成一定的正相關關系，其控制著余震的數目.即使是在相同的構造條件和相同的震級條件下，其參數也存在一定的差異，這在很大程度上取決于單個余震序列.包括日本對2004年Chuetsu 地震和2007 年的Chuetsu-oki 地震研究也獲得了類似的結論(JMA, 2009)，地震序列參數k是影響強余震數目的關鍵因素.

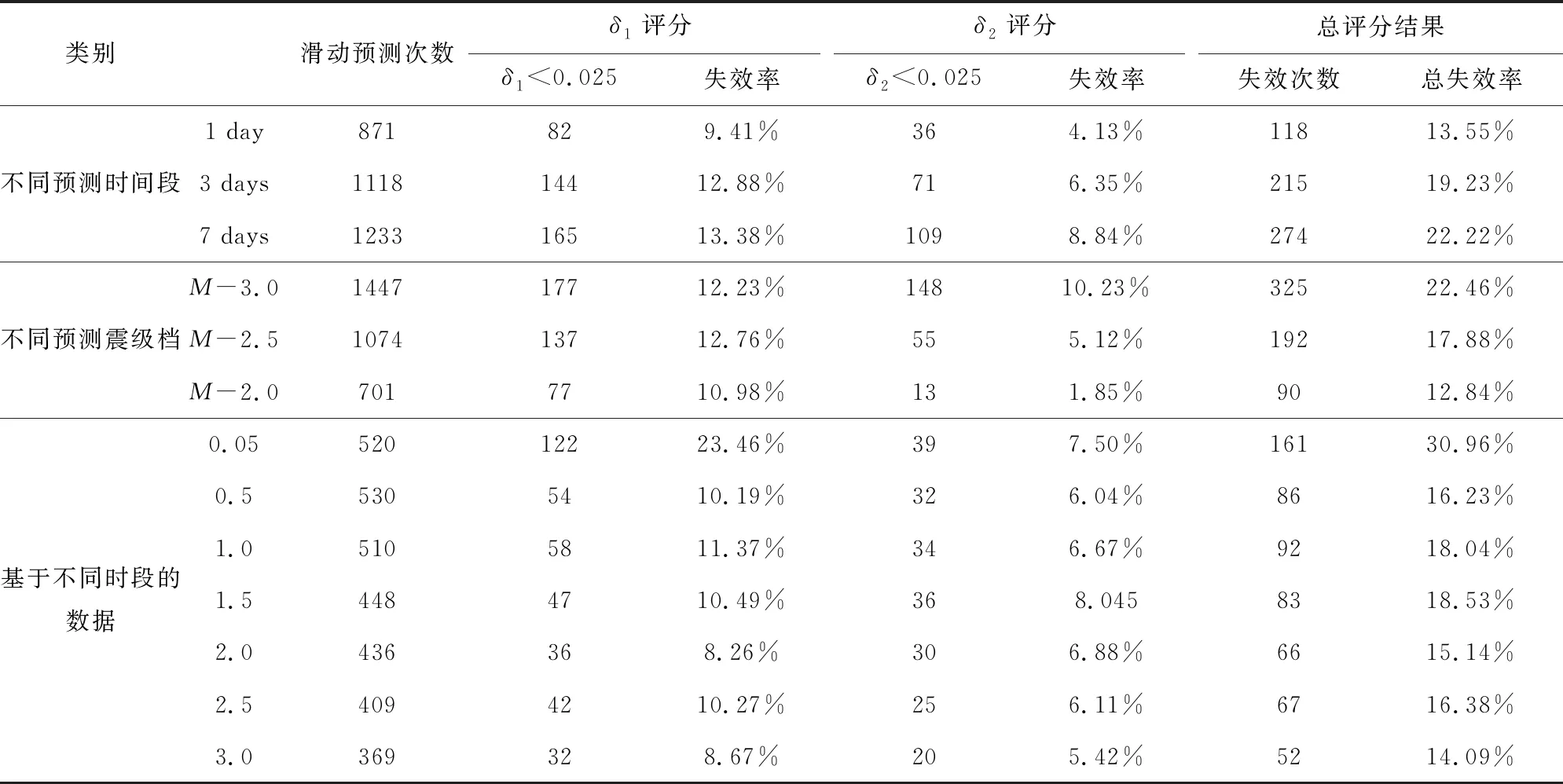
表3 中國大陸地區地震序列Omi-R-J模型效能評估統計結果Table 3 Statistical results of effectiveness evaluation of the Omi-R-J model in continental China

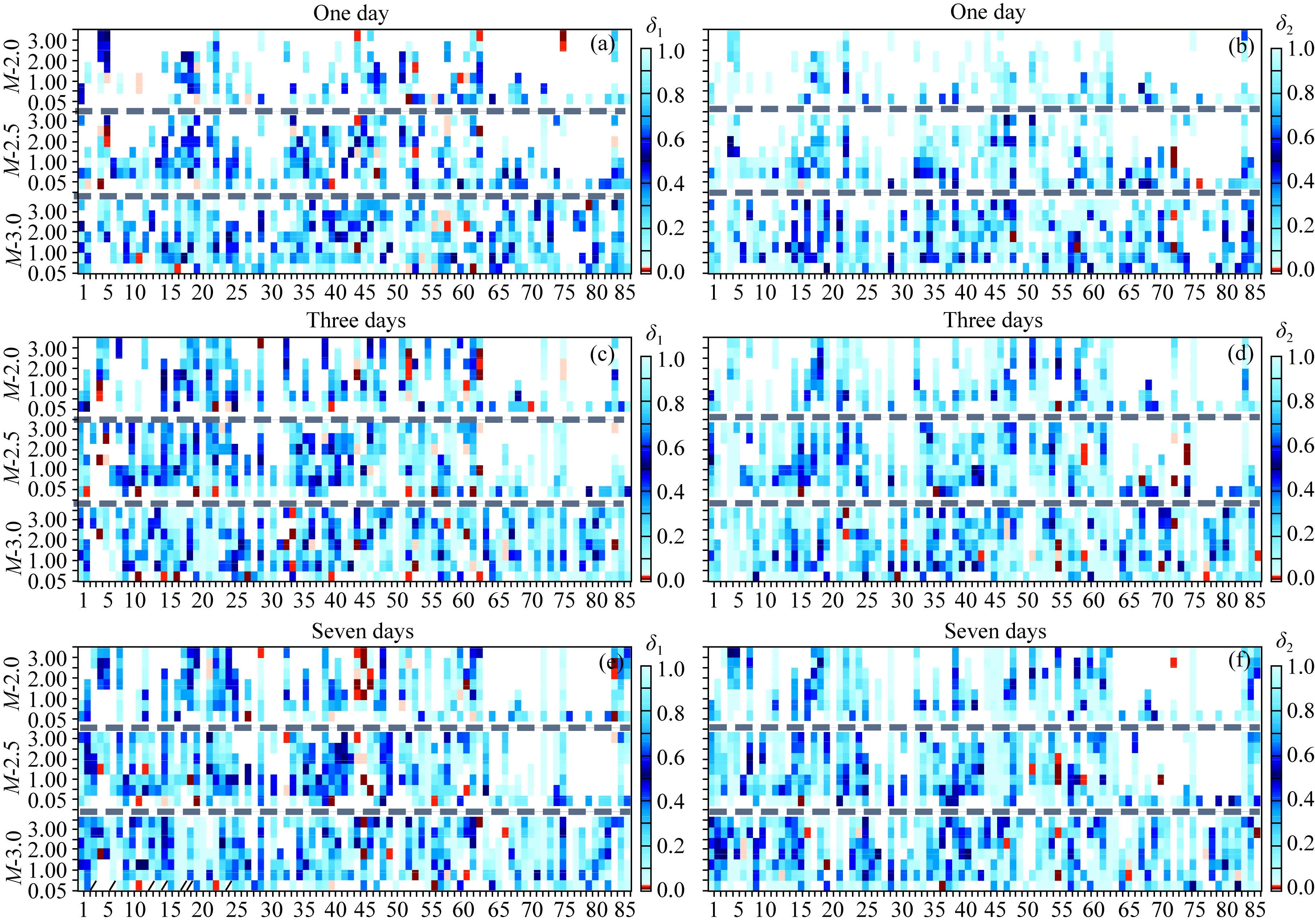
圖6 Omi-R-J模型強余震發生率預測的N-test統計檢驗結果(a)、(c)、(e)分別為Omi-R-J模型在不同震級檔下對未來1天、3天、7天的δ1評分結果；(b)、(d)、(f)分別為Omi-R-J模型在不同震級檔下對未來1天、3天、7天的δ2評分結果.圖中藍色色調代表在95%置信水平預測有效的時段，紅色色調代表δ1<0.025或δ2<0.025的結果，即預測失效的時段.空白區域為預測時段沒有發生一次預測震級以上的地震事件，斜線區域代表因數據不足原因無法參與計算的時段.Fig.6 N-test results for the strong aftershock forecasting based on the Omi-R-J model(a), (c) and (e) show δ1-score for future 1 day, 3 days and 7 days aftershock forecasting in different magnitudes, respectively. (b), (d) and (f) show δ2-score for future 1 day, 3 days and 7 days aftershock forecasting in different magnitudes, respectively. The blue block represents the period when the prediction is valid at 95% confidence level. The red block represents the result of δ1<0.025 or δ2<0.025, i.e. the forecasting period of failure. The blank area indicates that no earthquake events of or above forecasting magnitude have occurred in the forecasting period. And the slash area represents the time period that cannot participate in the calculation because of insufficient data.

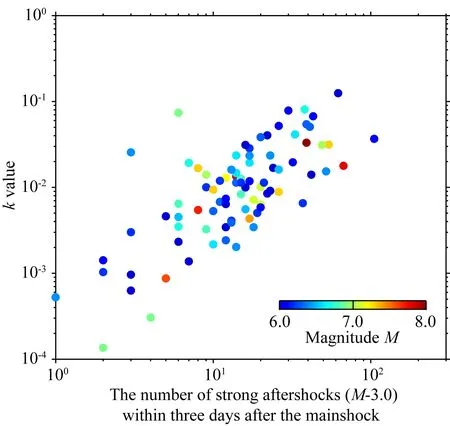
圖7 地震序列參數與震后早期強余震數目的關系顏色的深淺代表了主震震級的大小.Fig.7 The relationship between the sequence parameters and the number of strong aftershocks in the early stage after the mainshockThe color represents the magnitude of the mainshock.

在基于不同時間尺度、不同震級檔的條件下，隨著預測時長和震級檔的下調，預測有效率反而降低，這和之前的一些研究(蔣長勝等，2015; 畢金孟和蔣長勝，2017)相反，主要可能是因為預測時段次數的增加導致了失效率的增加.除基于0.05天的預測有效率低于80%外，其他預測時段的有效率均大于80%，從0.05天到0.5天預測失效率由30.96%下降到16.23%，隨著更多余震事件參與計算，地震的預測有效率得到顯著提升，早期有效率的偏低可能與參與計算的余震數目過少，即序列的發育程度有關.具體的基于不同時段、不同震級檔以及不同時段的預測失效次數和失效比例如表3所示.監測能力的顯著提升是提高余震概率預測有效性的重要因素之一(Bi and Jiang, 2020)，且對Omi-R-J模型比對包括ETAS、R-J模型依賴于完備性震級的影響稍小一些.蔣長勝等(2018)利用OK1993模型和事件“刪除”概率函數構建的隨機地震序列目錄測試結果表明，Omi-R-J模型對比于其他模型在余震監測能力有限的震后早期階段逐步恢復到震前水平過程中，具有更好的適用性.

5 結論

造成震害疊加效應和進一步加重次生災害的強余震，往往發生在震后的早期.為系統評估中國大陸地區強震的早期余震概率預測效能及制約因素，本文利用可充分考慮震后早期小震信息的Omi-R-J模型，對中國大陸的86個地震序列進行了系統性的預測研究，并利用N-test方法對預測結果進行了統計檢驗.獲得如下結論：

(1)利用Omi-R-J模型對中國大陸的強震序列進行分震級、分時段的預測結果顯示，Omi-R-J模型對中國大陸早期的強余震具有較好的預測能力，總的預測有效率為81.16%，平均預測有效率為83.82%，預測過少的比例大于預測過多的比例；對所選序列1天、3天和7天的預測平均有效率分別為88.90%、82.76%、80.82%；對不同震級檔[M-3.0,M-2.5,M-2.0]預測的平均有效率為78.89%、86.14%、92.35%；基于震后早期不同時段([0.05, 0.5, 1.0, 1.5, 2.0, 2.5, 3.0])預測的平均有效率為84.31%、92.06%、91.12%、90.74%、92.49%、91.87%、92.90%.

(2)通過分析震后早期1天和30天數據擬合參數的相關性發現，b、k、c在早期與此后更長的序列持續時間具有較強的相關性，差異較小，表明Omi-R-J模型可在震后早期記錄相對不完整的階段更早的獲得較為穩定的序列參數. 更重要的是，這也意味著在震后1天內即可對震源區應力狀態、余震觸發能力獲得可靠認識，這對強余震危險性研判和震后應急處置有重要意義；而p值的相關性弱，可能與p值表示的是余震活動的長期衰減特性、需要較長時間的數據來精確估計有關.由此表明在提升早期余震概率預測的準確性上，需要更為關注主震后p值的動態變化.

(3)地震序列參數k是影響地震數目的關鍵因素，而震后余震序列的發育程度可能是制約震后0.05天地震預測有效率重要因素之一.由此也表明除了利用類似于帶有克服早期余震序列缺失問題的技術優勢的Omi-R-J模型外，繼續從利用模板匹配濾波、深度學習等技術提高早期余震的檢測率也是提高余震預測效能的重要途徑.

致謝研究中使用了中國地震臺網中心“全國地震編目系統”提供的“統一正式目錄”，日本東京大學生產技術研究所Takahiro Omi博士為本研究提供了程序和技術支持，兩位評審專家提出了諸多建設性修改建議、對稿件質量提升幫助很大，在此一并表示感謝.