延時網絡控制系統的魯棒L1控制器設計

梁艷，崔巖巖

(大慶技師學院機電工程系，黑龍江大慶，163255)

0 引言

網絡控制系統(Networked Control Systems,簡稱NCS),是隨著計算機技術、控制科學工程以及網絡通訊等各學科技術不斷發展而興起綜合產物。在某一區域內的網絡條件下，NCS是傳感器、執行器、控制器主要功能部件以及通信網絡相連接進行信號交換和傳輸的集合,這樣不同地點的用戶在這一區域內可在實現資源共享的同時進行協調操作以及對實時反饋控制系統的全網絡化[1][2]。NCS與點對點結構的傳統系統相比而言，優勢在于實現了遠程控制與操作，而且還增加了系統的可靠性和靈活性，但同時由于在數據傳輸過程中，帶寬局限性、傳輸路徑的不確定性等諸多因素都會導致信息在傳輸過程中有等待、阻塞以及丟失的現象出現，延時的產生則不可避免，而且在多數情況下，也是不可忽略的，因而成為國內外研究的熱點。目前，NCS的實際應用遠遠領先于其控制理論的研究，使得控制理論發展面臨著嚴峻的挑戰，針對網絡控制系統目前的研究現狀，對其理論研究和分析就具有及其重要的現實意義。

穩定性是系統的重要特性，也是在控制理論研究和控制系統設計中最基本問題。在經典控制理論中，雖然建立了根軌跡判據、奈奎斯特穩定判據等各種判據來分析判定線性時不變控制系統的穩定性，但是它不能實現最優控制；在現代控制理論中，俄國學者李雅普諾夫（Lyapunov）采用狀態變量對系統進行描述，求解系統方程來判定收斂性，分析和設計方法更具準確性，從而提出了確定系統穩定性理論，能夠實現最優控制；不僅適用于線性、時不變、單變量系統，而且還適用于非線性、時變、多變量系統。系統的Lyapunov穩定性[3]是指系統在運行過程中，受長時間擾動的影響，原來的平衡狀態被打破后再次恢復到平衡狀態的能力。

L1（峰值-峰值）控制問題是相對于持續有界擾動輸入設計一個控制器在最劣情況下時滯系統輸出信號的最大幅值。近年來，根據線對性矩陣不等式技術研究，國內外學者采用峰值-峰值設計方法已經對濾波、降階等問題進行了研究，但都基于一般系統。因此，對于延時網絡控制系統的峰值-峰值優化問題的研究仍是一項重要工作。

本文針對延時網絡控制系統,研究了魯棒峰值-峰值控制問題。首先基于參數依賴Lyapunov函數思想以及線性矩陣不等式技術[4]，得出延時網絡控制系統的峰值-峰值性能判據，在保證閉環系統漸近穩定的條件下，設計控制器，這種算法降低了其保守性。將L1性能約束引入延時網絡控制系統的魯棒控制中，設計魯棒L1控制器[5]保證閉環系統漸近穩定且具有L1性能約束[6][7]。

1 問題描述

在網絡控制系統[8]中由于有多節點共享網絡，網絡帶寬等多方面的限制，信息在傳輸過程中，不可避免出現交叉碰撞和連續重發的現象，這樣信息在傳輸時，就會發生數據包的丟失和延時。圖1為數據包丟失的延時網絡控制系統，圖2為圖1的等效圖。

圖1 數據包丟失的延時NSC

下面對圖2的等效網絡控制系統進行分析。

這樣，將具有數據包丟失和網絡延時的網絡控制系統重新構建的數學模型，就轉變為具有隨時間變化的時變時滯系統

2 延時網絡控制系統L1控制器設計

當延時NCS閉環系統(1)漸近穩定且具有L1性能準則，對狀態控制器進行求解，這時控制器參數K為待求變量，這樣我們推算所求的矩陣不等式LMI就變成了雙線性矩陣不等式，下面針對NCS構建的數學模型（1）的控制器進行求解，給出下面的如下定理。

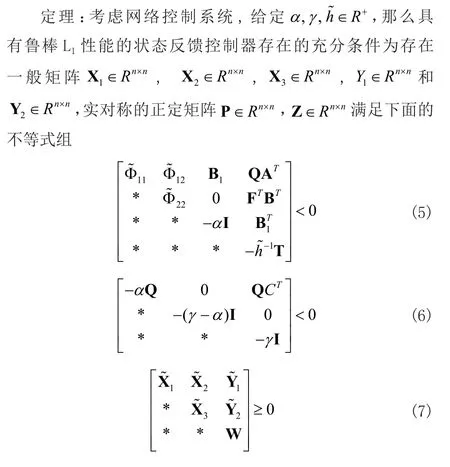
注：L（1峰-峰）增益的上界γ的最小值取決于于α的選擇，為了獲得更緊的γ界，需要對α執行的一個線性搜索。盡管在很大程度上，錐補線性化（CCL）算法能夠找到全局最優解，但不能保證總是全局最優且收斂，所以通過算法1所求的可行性解是次優的。

3 數值算例

考慮延時網絡控制系統的被控對象的狀態方程為

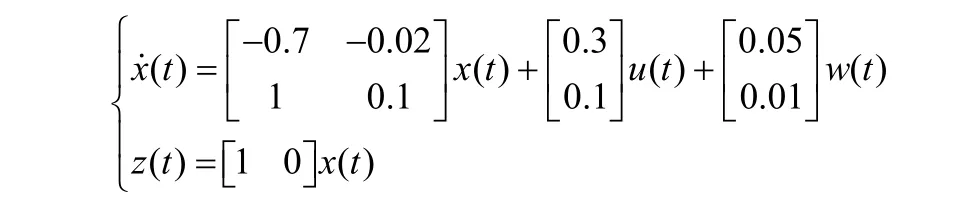
通過上述定理的算法1，γ= 6 ,α=0.2通過MATLAB進行求解，可以得到延時網絡控制系統控制器的可行性解。

圖3 閉環系統的狀態

3 結束語

本文研究了延時NCS的魯棒L1控制器設計，根據Lyapunov穩定性理論、魯棒L1性能指標以及運用錐補線性化（CCL）算法得出其L1控制器的設計方法并對其進行求解，用MATLAB進行仿真，從而驗證該設計方法的有效性和可行性。