雙層框架鐵路對鄰近建筑物的振動影響

陳以庭 馮讀貝 楊吉忠 金旭煒

(中鐵二院工程集團有限責任公司， 成都 610031)

為提高城市建成區既有單線走廊的運輸效率，在有限空間內將單線擴建為地上、地下單線的雙層布置形式成為一種可能，需確定雙線框架結構鐵路對鄰近住宅建筑物的振動影響，但目前尚無案例和相關標準可參考。近年來，針對車致振動的影響開展了大量的研究，王祥秋[1]等對廣州金沙隧道往廣州南站方向270 km/h高速列車引起建筑物響應進行現場實測，得到列車產生振動頻率集中在25～60 Hz范圍內，鉛垂向Z振級達到70.62 dB，建筑物二次振動具有明顯高度放大效應；張凌[2]等對南昌西站候車廳車致振動進行現場實測，發現梁柱結構的約束作用對高于40 Hz的高頻振動傳播抑制明顯；Connolly[3-4]等對歐洲7國17個高速鐵路車站點進行現場測試，基于頻譜分析獲得近場傳播頻率集中在15～30 Hz范圍內，27～31 Hz內有明顯峰值。

關于既有鐵路擴建為地上、地下單線雙層鐵路的車致振動影響研究，目前在國內、外相關領域尚屬空白，且本工程鐵路與兩側建筑物的距離較近，因而難以確定其運行后對沿線建筑物的振動影響。針對這一問題，本文采用有限元和車輛-軌道耦合動力學理論，建立列車-軌道-單線雙層框架橋-大地-建筑物三維耦合動力學模型，分析既有鐵路改擴建后列車運行引起的振動對沿線建筑物的影響，相關研究成果可為既有鐵路改擴建提供參考。

1 工程概況

某新建高速鐵路利用既有鐵路引入城區樞紐車站，需將區間單線鐵路擴建為雙線，同時綜合考慮線路區間復雜工程，采用地面、地下單線雙層框架結構實現既有鐵路通達范圍內增建1條鐵路，上、下層線路軌面標高相差約9.0 m。為減少對既有建筑物的影響，框架橋邊墻外側設置圍護墻，圍護墻寬1.0 m，深13.0 m，底部坐落于弱風化泥質粉砂巖層中。框架橋空腔內部為下層鐵路，地面為上層鐵路，上、下層鐵路道床均采用碎石道砟，線路運行CRH380系列動車組，8輛編組，路段限速80 km/h。擴建區段穿越城區，沿線居民樓等振動敏感建筑分布居多，最近距離為7.0 m，建筑結構形式包括砌體結構和框架結構，基礎形式多為條形基礎和獨立基礎，均坐落于軟土層中。擴建區間橫斷面如圖1所示，沿線建筑物情況統計如表1所示。

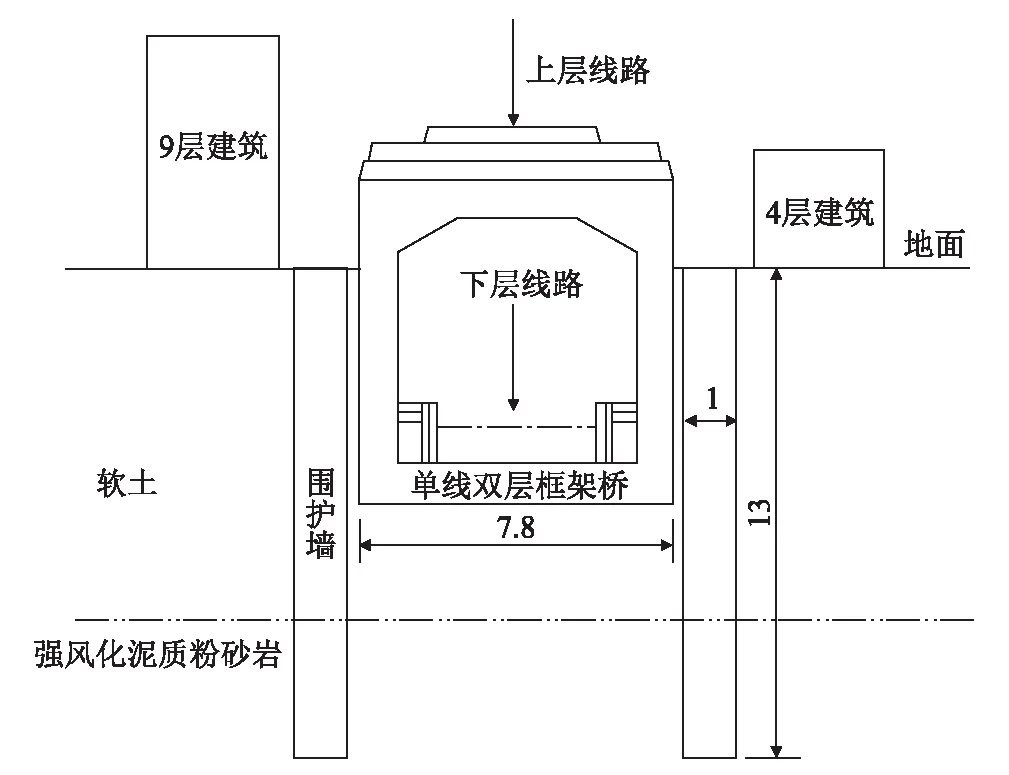
圖1 擴建區間橫斷面示意圖(m)

表1 建筑物情況統計表

2 動力計算模型

2.1 列車-軌道模型

基于車輛-軌道耦合動力學理論[5]，建立列車空間動力學模型，通過列車-軌道分布式仿真平臺[6]實現車輛運行行為的模擬，在輪軌接觸模型中采用Hertz非線性彈性接觸理論確定輪軌法向力：

(1)

式中：G——輪軌接觸常數;

φZ(t)——輪軌之間的彈性壓縮量(m)。

根據Kalker線性理論計算輪軌蠕滑力，然后采用沈式理論[7]進行非線性修正。

根據城市軌道交通軌道平順性的特點及振動關注的4～200 Hz頻段，本文采用鐵道科學研究院提出的垂向短波不平順的功率譜密度函數，可近似表達為：

S(f)=0.036f-3.15

(2)

式中：S(f)——不平順的功率譜密度函數(mm2/(1/m))；f是空間頻率(1/m)；其波長范圍為0.01～1 m。

對于大于1.0 m波長范圍的不平順功率譜密度表達為：

(3)

式中：A、B、C、D、E、F、G——軌道不平順功率譜密度的特征參數，對不同線路和不同類型的軌道不平順有不同數值。

2.2 建筑物有限元模型

根據擴建區間建筑物的統計情況，建立4層砌體、4層框架、9層框架結構有限元模型。4層砌體結構層高3.0 m，基礎形式為條形基礎，埋深1.6 m，墻體為0.24 m厚砌體；4層框架結構層高3.0 m，基礎形式為柱下獨立基礎，埋深2.0 m；9層框架結構第一層為車庫，層高為2.2 m，2～9層為住宅，層高3.0 m，整體為現澆鋼筋混凝土結構，基礎為柱下獨立基礎，埋深3.0 m。有限元模型中構造柱、圈梁、框架梁、柱均采用梁單元模擬，樓板、墻體均采用殼單元模擬。

2.3 鐵路-單線雙層框架橋-大地-建筑物三維模型

大地模型采用實體單元模擬，整體模型尺寸沿軌道方向取200.0 m，垂直于軌道延伸方向取145.0 m，豎向取31.5 m，模型中包括單線雙層框架橋，埋深7.5 m，地表以上部分2.0 m，圍護墻貫穿軟土層，伸入到強風化泥質粉砂巖中3.0 m。單向雙層框架橋-大地-建筑物三維模型如圖2所示，動力學模型土體計算參數如表2所示。土體網格尺寸受輸入最短波長的限制，根據研究表明[8]，網格尺寸須小于輸入波形最短波長的1/8～1/10，且為能精確獲得波動結果，單元尺寸應滿足以下要求：

表2 動力學模型土體參數表

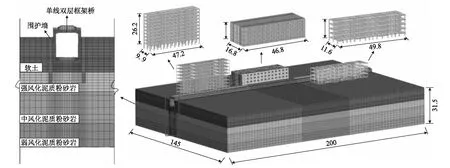
圖2 單線雙層框架橋-土體-建筑物三維模型圖(m)

(4)

式中：Δx——模型網格劃分單元尺寸；

Cs——土層的剪切波速(m/s)；

fmax——分析時的上限頻率(Hz)。

本文土體模型單元尺寸取0.15～3 m，在遠離單線雙層框架橋和建筑結構位置的土體網格逐漸放大，可滿足計算的需要。

進行動力計算分析時，需在模型外圍添加三維粘彈性人工邊界[9]，用來模擬模型以外的半無限空間土體，防止在邊界上發生波的反射造成計算失真，人工邊界等效為連續分布的并聯彈簧-阻尼器系統，切向與法向的彈簧剛度和阻尼系數按照式(5)和式(6)取值：

(5)

(6)

式中：KBN、BBT——分別為彈簧法向與切向剛度；

CBN、CBT——分別為阻尼器法向與切向的阻尼系數；

R——波源至人工邊界的距離；

cs和cp——分別為S波和P波波速；

G——介質剪切模量；

ρ——介質質量密度；

αT與αN——分別為切向與法向粘彈性人工邊界修正系數，本文選取αT=1.33、αN=0.67。

動力分析中需要設定阻尼保證計算結果的準確性，本文中采用Rayleigh阻尼來計算，其假設結構阻尼矩陣是質量矩陣和剛度矩陣的組合，滿足：

[C]=α[M]+β[K]

(7)

式中：[C]、[M]和[K]——分別代表體系的阻尼矩陣、質量矩陣和剛度矩陣;

α——質量阻尼系數，取α=2.46

β——剛度阻尼系數,取β=7.8e-5。

3 建筑物振動響應

基于構建的三維耦合動力學模型，考慮此擴建區間列車上、下層線路運行的實際情況，分別對3種工況條件下列車運行對建筑物的振動影響進行分析，列車運行工況如表3所示。建筑物測點的選取位置均為距線路中心相同的樓板跨中，建筑物測點布置如圖3所示。

表3 列車運行工況表

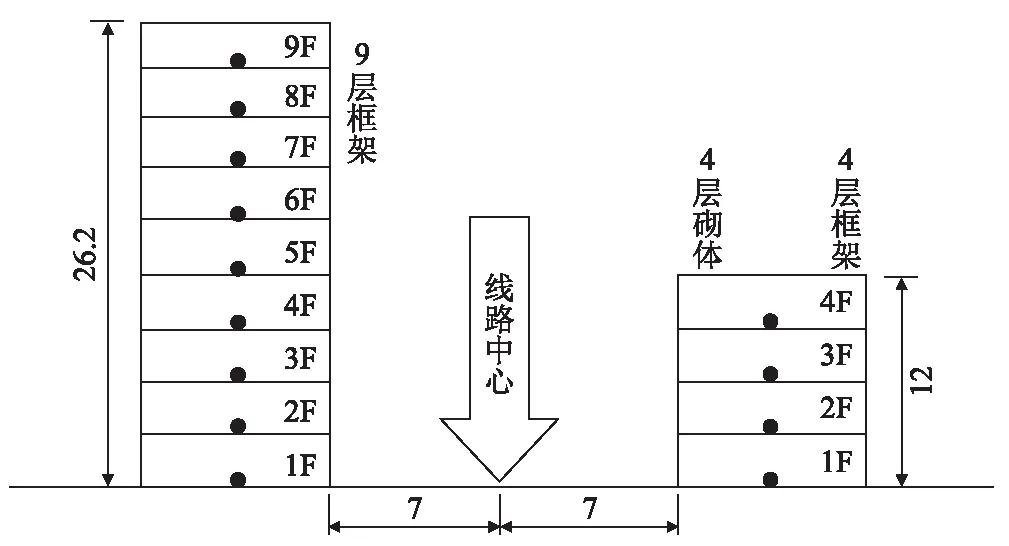
圖3 建筑物測點布置圖(m)

3.1 峰值振動加速度

列車不同運行工況下建筑物各層測點峰值振動加速度如圖4所示。從圖4可以看出，當列車在此擴建區間內運行時，工況1的振動響應最小，工況3的振動響應最大，峰值振動加速度在建筑物首層出現最大值，在2～3層大幅度衰減，說明振動由底部向上部樓層傳遞時，在低樓層處會過濾大部分振動。從圖4(a)和4(b)可以看出，振動在4層磚混結構內向上部傳播時不斷減小，在4層框架結構內向上部傳播時先減小在頂層有放大現象，說明相同層高條件下框架結構隨樓層的增加具有更強的振動傳遞性。從圖4(c)可以看出，車致振動在9層框架內由底部向上部傳播時，4～8層峰值振動加速度趨于一致，在頂部出現小幅度的增加。

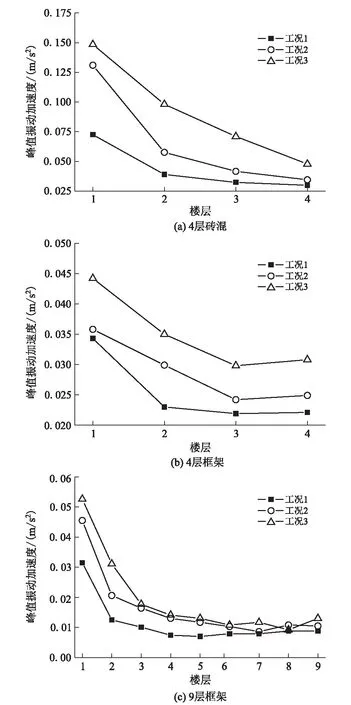
圖4 建筑物測點峰值振動加速度圖

3.2 振動加速度頻域分析

4層砌體和框架結構建筑物首層測點不同工況下頻域振動加速度如圖5所示，因列車在大部分時間內為單一方向行駛，且工況2振動響應大于工況1，故對9層框架工況2的振動頻域幅值進行研究，如圖5(c)所示。

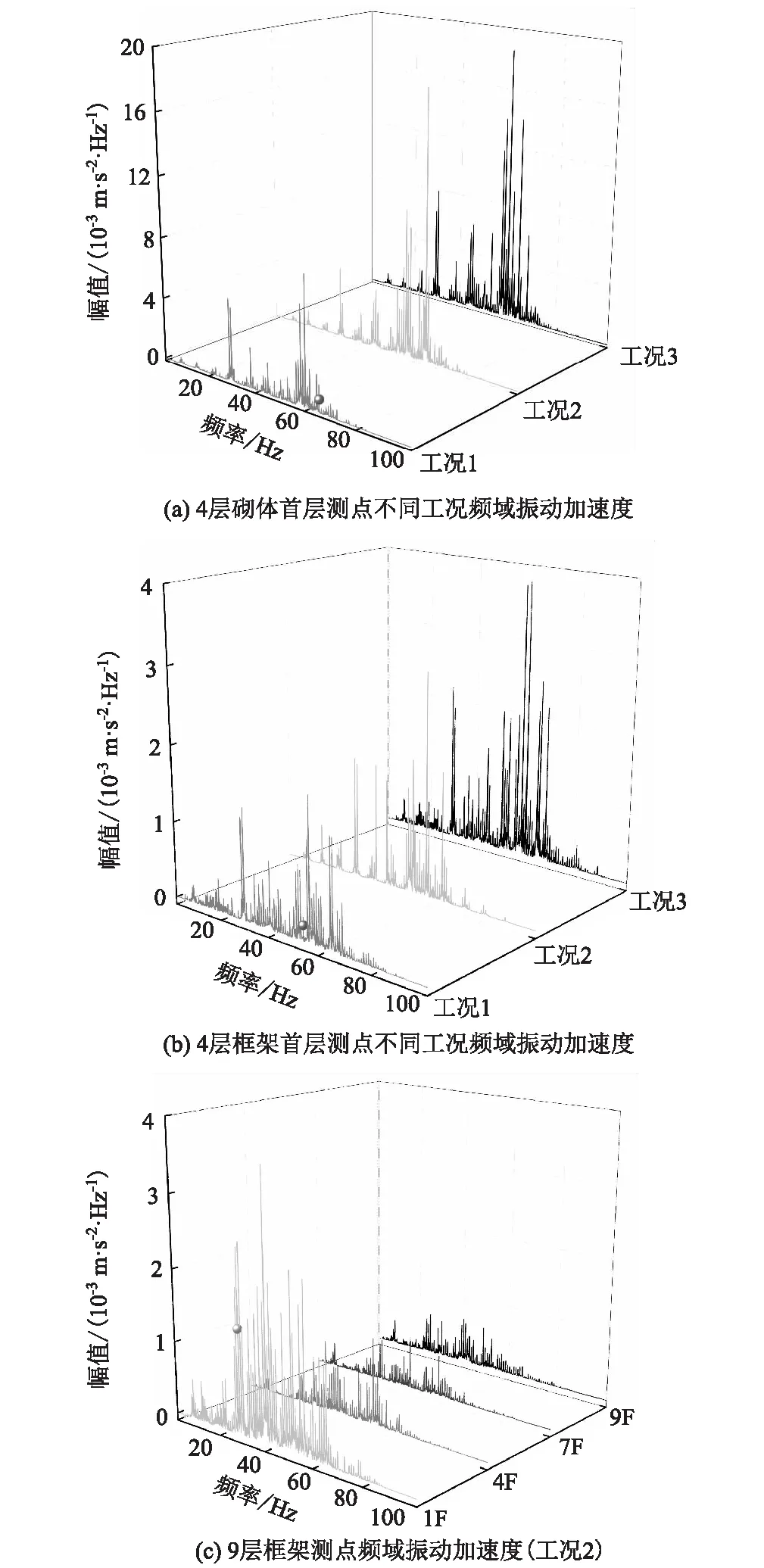
圖5 建筑物測點頻域振動圖

從圖5(a)和圖5(b)可以看出，建筑物車致振動影響加速度幅值工況3明顯大于工況1和工況2，但振動加速度頻域分布規律基本一致；列車運行引起的振動對砌體結構的頻域影響范圍集中在50～70 Hz范圍內，振動主頻在60 Hz左右；列車引起的振動對框架結構的頻域影響范圍集中在30～70 Hz范圍內，振動主頻在58 Hz左右，由此說明振動對框架結構的頻域影響范圍更大，但加速度幅值更小。

從圖5(c)可以看出，在工況2條件下，9層框架車致振動主頻集中在40 Hz左右，但加速度幅值從2～4層大幅度減小，頂部趨于一致。振動隨高度向上部的傳播過程中大于60 Hz頻率范圍的加速度幅值衰減較快，4～20 Hz頻率范圍內的加速度幅值衰減緩慢，隨著樓層的增加振動頻率影響范圍逐漸減小。

3.3 1/3倍頻程振動加速度級

為確定列車運行引起的振動對建筑物樓板在頻域上的分布，對車致振動響應進行1/3倍頻程分析。列車在不同運行工況下建筑物測點的1/3倍頻程振動加速度級如圖6所示。工況2時4層砌體、框架首層測點1/3倍頻程振動加速度級如圖7所示。

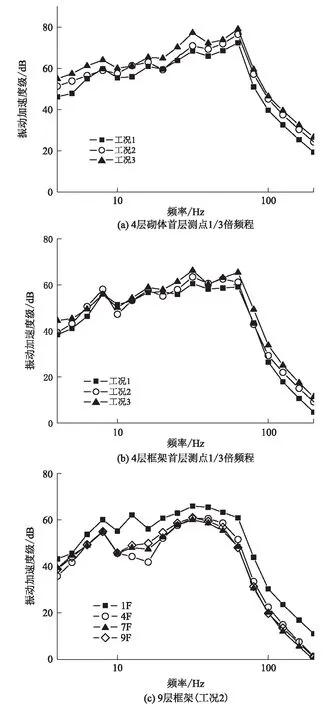
圖6 建筑物1/3倍頻程振動加速度級圖

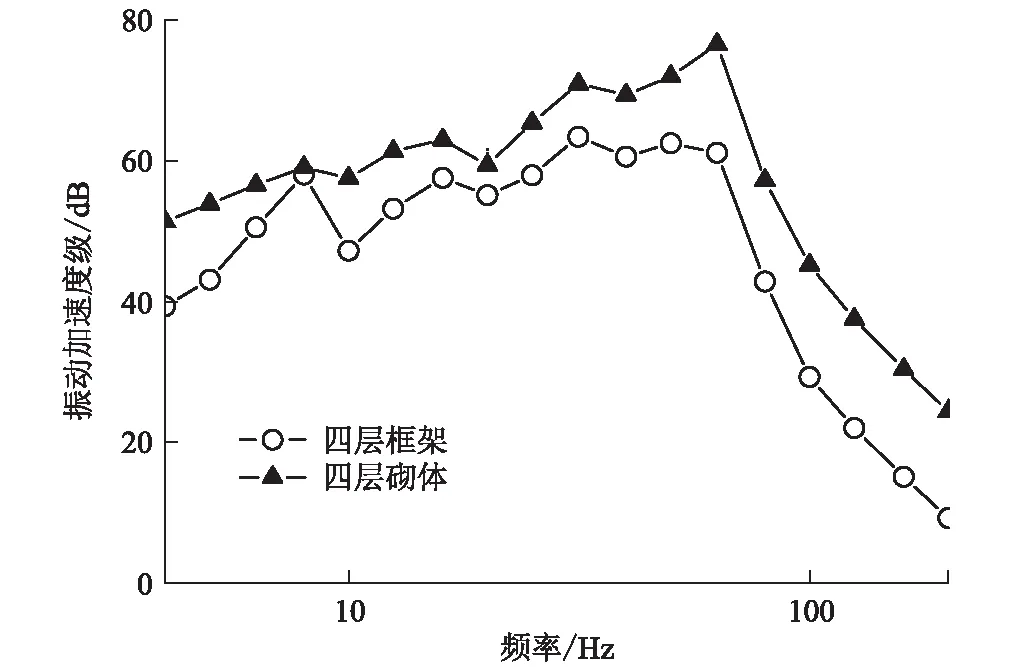
圖7 4層砌體、框架首層測點1/3倍頻程振動加速度級圖(工況2)

從圖6(a)可以看出，4層砌體結構首層測點在3種工況條件下振動加速度級峰值出現在8 Hz、31.5 Hz和63 Hz處，最大振級在63 Hz左右，工況3最大振級比工況2高 2.5 dB，比工況1高6.7 dB。從圖6(b)可以看出，4層框架結構首層測點在3種工況條件下振動峰值主要出現在8 Hz、16 Hz、31.5 Hz和63 Hz處，最大振級出現在31.5 Hz左右，工況3最大振級比工況2高2.8 dB，比工況1高5.7 dB，工況2在8 Hz附近振級超過工況3。從圖6(c)可以看出，工況2的9層框架首層測點振動加速度級在4～200 Hz頻率范圍內明顯大于其他樓層約5 dB，樓板的振動加速度級峰值主要集中在31.5 Hz處，隨著樓層的增加大于 60 Hz的振動有所衰減，4～20 Hz范圍內的振動有所增加。

從圖7可以看出，工況2砌體結構與框架結構的振動加速度級幅值變化趨勢基本一致，在4～200 Hz頻域范圍內，層高相同、用途一致、距線路中心相同的砌體結構比框架結構振動加速度級平均高約10 dB。框架結構首層測點在8 Hz附近振動顯著，此頻段振動加速度級趨近于砌體結構首層測點。

通過上述分析可知，列車上、下層鐵路同時運行引起振動對建筑物影響最大，上層線路運行引起的振動最小，下層線路運行引起的振動大于上層線路運行；建筑物首層測點1/3倍頻程振動加速度級均在8 Hz與63 Hz頻率左右出現峰值。振動加速度級在大于80 Hz的頻率范圍大幅度衰減。

4 建筑物振動評價

本文參考JGJ/T 170-2009《城市軌道交通引起建筑物振動與二次輻射噪聲限制及其測量方法標準》[10]振動影響區域分類，選取2類區域進行鐵路沿線建筑物的振動評價，其適用范圍為居住、商業混住區，商業中心區，晝、夜間最大分頻振動加速度級分別為70 dB和67 dB，既有沿線建筑物應當按照2類夜間標準控制。

建筑物各樓層測點分頻最大振級隨著樓層的變化如圖8所示。從圖8(a)可以看出，在相同的運行工況下，4層砌體建筑物各樓層分頻最大振級比4層框架建筑物平均高約10.4 dB。3種工況4層砌體結構的分頻最大振級均超出夜間限值，首層樓板的環境振動在工況1、工況2和工況3條件下分別超出夜間限值5.4 dB、9.6 dB、12.1 dB，分頻最大振級隨著樓層的增加，出現逐層衰減的現象，從首層至頂層衰減的程度達到4.7～7.4 dB；4層框架結構分頻最大振級在3種工況條件下均未超出夜間限值，振動加速度級首層位置最大，隨著樓層的增加，2、3層出現衰減，頂層的樓板呈現輕微的放大現象。

圖8 建筑物3種工況下各樓層分頻最大振級圖

從圖8(b)可以看出，9層框架分頻最大振級在3種工況條件下均未超出夜間限值，各樓層測點分頻最大振級從首層開始至5層減小達5.2～6.3 dB，6～9層出現小幅度的放大現象，放大幅值達到1.2～1.7 dB。

針對擴建區間列車運行對既有砌體建筑物振動超標的現象，有必要采取一定的減隔振措施，減小列車運行對既有砌體建筑物的影響，為后續既有線路的擴建改造提供指導意義。

5 結論

經由上述分析，可得到如下結論：

(1)列車以80 km/h的設計速度運行通過擴建區間，上、下層線路同時運行引起的振動對建筑物的影響最大，上層線路運行時對建筑物的影響最小，下層線路運行對建筑物的影響大于上層線路運行。

(2)列車運行引起的振動對距離線路中心相同的4層砌體影響大于4層框架，在相同運行工況下，砌體建筑物分頻最大振級比框架建筑物平均高約10.4 dB。

(3)框架建筑物比砌體建筑物隨樓層的增加具備更強的振動傳遞性，列車振動對砌體建筑物的影響從首層開始隨著樓層的增加逐漸減小，對框架建筑物的影響從首層開始隨著樓層的增加出現先減小后放大的現象。

(4)列車在擴建區間運行時4層、9層既有框架建筑物的環境振動均在夜間限值內，4層砌體建筑物的環境振動超出夜間限值，其首層樓板的環境振動在列車上層線路運行、下層線路運行、上層線路和下層線路同時運行時分別超出夜間限值5.4 dB、9.6 dB和12.1 dB，有必要采取一定的減隔振措施，減小列車運行對既有砌體建筑物的影響。