考慮預期功能安全的智能汽車自動緊急制動系統*

談東奎，胡港君，朱 波，金 來，張 捷

（1.合肥工業大學汽車工程技術研究院，合肥 230009；2.安徽三聯交通應用技術股份有限公司，合肥 230081；3.公安部交通管理科學研究所，道路交通安全公安部重點實驗室，無錫 214151；4.合肥工業大學智能制造技術研究院，合肥 230051）

前言

傳統的自動緊急制動系統一般基于安全距離模型進行避撞決策，但在實際道路中，由于場景的復雜性和自身系統性能受限，自動緊急制動系統依然可能發生失效而導致不安全事故發生，此類在系統內部組件并未發生故障的情況下由外部環境擾動、系統功能局限或人為誤操作導致的安全問題被稱為預期功能安全。智能汽車作為一個智能個體，內在的復雜性和不確定性決定了它的安全性分析重點不同于傳統汽車的質量保障領域，而是非故障安全領域。預期功能安全技術為智能汽車在非故障情況下提供了安全保障，是當前國內外學者重點關注和研究對象。

Mirko在文獻［4］中闡述了功能安全和預期功能安全之間的關系，John提出了預期功能安全風險評估框架，豐富和擴展了預期功能安全概念的內涵。BOCH 公司把預期功能安全用于ADAS 系統的開發過程，并利用故障樹分析方法來分析DA/AD 系統，但故障樹作為傳統的安全分析方法，依然是基于可靠性理論分析安全性，無法涵蓋預期功能安全領域問題。2011 年，Leveson提出的STPA 方法被開始用于分析汽車預期功能安全問題。Mahajan 等運用STPA對車道保持系統進行安全性分析，提出了系統改進的安全要求。陳君毅等基于STPA 提出了一種面向高等級自動駕駛決策系統的安全性開發方法，對泊車系統進行了系統改進。

上述有關預期功能安全的研究雖取得一定理論性進展，但在運用到ADAS 系統開發過程中依然存在以下不足：預期功能安全性在ADAS 系統開發中如何量化以保證車輛正常安全行駛的問題沒有探討；未能通過試驗對比驗證考慮預期功能安全的ADAS系統的有效性。

本文針對以上不足，在傳統自動緊急制動系統的基礎上考慮了預期功能安全，利用STPA對系統進行安全分析，得出了系統的預期功能安全要求。然后圍繞感知盲區安全車速，建立車輛與盲區內潛在行人橫穿馬路的相遇運動學模型，計算出不碰撞行人最高車速，再加入感知盲區面積變化率、城市道路限速與最低車速等因素，綜合考慮得出盲區最佳安全車速變化曲線模型，接著設計速度滑模控制器跟蹤該速度，最后分別在CarSim 仿真平臺和在環仿真臺架上驗證了該安全策略的有效性。

1 自動緊急制動系統安全分析

1.1 基于STPA的安全分析方法

對于智能汽車而言，與預期功能安全有關的風險，只從獨立的組件出發設計系統需求是難以發現解決的。STPA 將重點從可靠性理論轉移到系統理論并關注組件交互事故和組件故障，實現安全性和可靠性的分離，既能解決功能安全領域問題，又能處理預期功能安全領域問題。

STPA 將安全定義為一個控制問題，把危害歸結為系統設計和運行缺少安全限制的原因，通過控制系統的行為來限制系統的安全。其安全分析流程主要分為4個步驟：

（1）明確系統的功能；

（2）建立系統控制結構；

（3）識別不安全控制行為，確定危險事件；

（4）分析危險事件發生的原因，提出安全要求。

1.2 自動緊急制動系統的安全分析

自動緊急制動系統的功能為減速避障，其輸入為車輛當前速度與障礙物位置，輸出為目標速度。利用STPA對其進行安全性分析，可以得到自動緊急制動系統的不安全控制行為及其不安全控制行為原因，見表1。前3種均為系統組件因故障而造成的危險，屬于功能安全問題，最后一種是由于外部遮擋物的存在和傳感器自身性能的限制而產生的感知盲區現象，屬于預期功能安全問題。

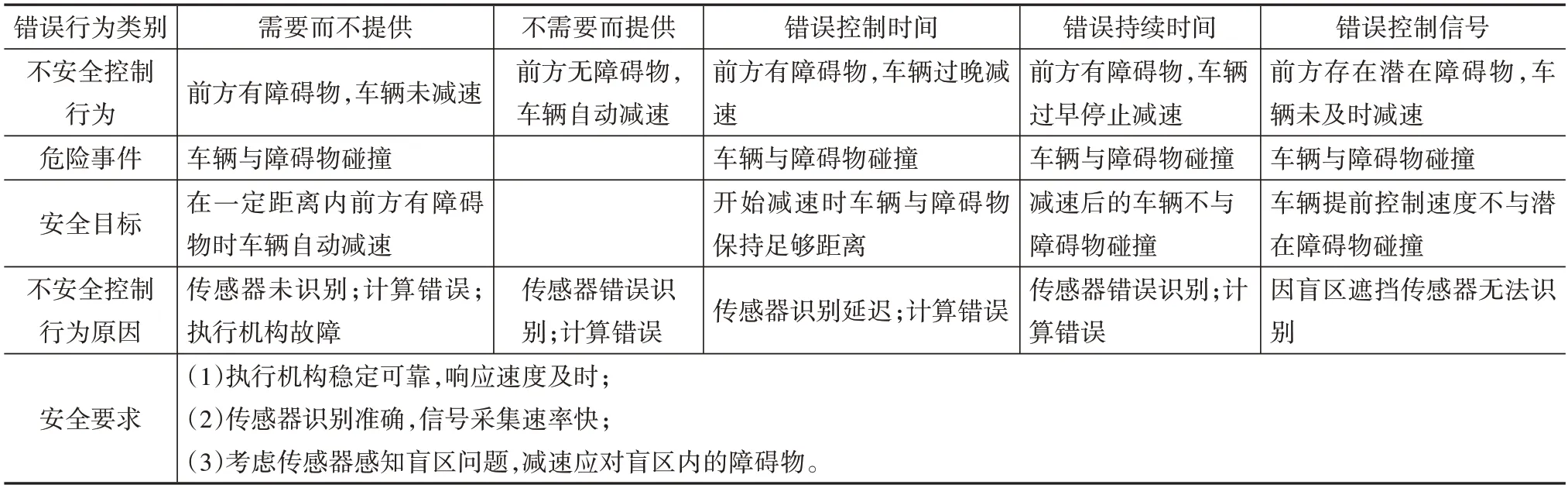
表1 自動緊急制動功能安全分析

安全分析結果表明要想解決感知盲區帶來的預期功能安全問題，須在傳統的自動緊急制動系統里加入感知盲區車速規劃策略，提前減速來應對潛在的障礙物。

2 盲區場景下車輛安全車速決策

針對感知盲區現象，國內外多采用V2X 技術解決傳感器性能不足的問題，但成本高昂，短時間難以實現。Yoshihara 等和Morales 等分別提出了基于Frenet 框架的安全駕駛模型和提取人類駕駛特征的強化學習模型，模擬專家駕駛員遇到盲區的行駛速度，但模型過于保守，極大影響車輛在盲區下的通行速度。袁朝春等將傳感器感知盲區邊緣線作為障礙物，根據邊緣線的運動變化，建立安全距離模型避免車輛發生追尾事故，但沒有考慮盲區下的人車相遇場景。

基于以上研究的不足，為對突然出現的行人進行安全避撞，考慮盲區對車輛的速度影響，尋求一個緊急制動前的車輛安全車速顯得至關重要。

2.1 盲區場景下車輛-行人運動學模型

車輛在與盲區內的行人相遇前，為兼顧安全性和通過時長，車速應盡可能在避免碰撞行人的基礎上保證更高；出于對行人發現車輛后可能做出加速向前奔跑的躲避行為的考慮，車輛應優先讓行人通過。根據以上兩點行車原則，可將車輛在盲區內的運動過程分為兩個階段：

（1）階段1，車輛沒有遇到盲區內行人，保持一個較高車速；

（2）階段2，車輛感知到行人，進行緊急制動，最后在行人橫穿軌跡線前停止，并建立以下模型，如圖1所示。

圖1 盲區場景下車輛與行人相遇運動學模型

車輛從點勻速沿軸方向運動，同時盲區內處一行人勻速沿軸方向運動，時間后，車輛到達點，行人到達點，車輛傳感器剛好檢測到行人闖入，自動緊急制動系統觸發，車輛以最大加速度緊急制動，在點處前停止運動。人-車相對關系有：

式中：v為車輛行駛速度；a為車輛制動減速度；為車輛從進入盲區到發現行人后經過時間；為行人與車輛的縱向距離。

根據正弦定理有：

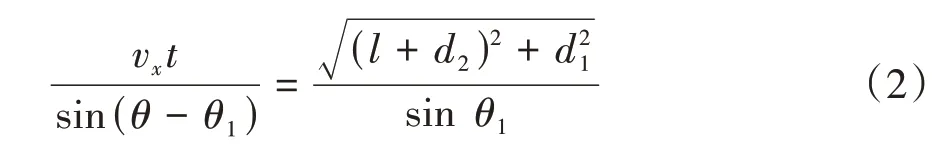
其中：

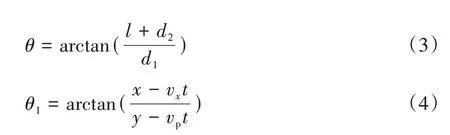
式中：為盲區縱向長度；為車輛傳感器與盲區的橫向距離；為車輛傳感器與盲區的縱向距離；為行人速度，1.5 m/s；為行人與車輛的橫向距離。

聯立式（1）～式（4），可求得不碰撞行人最高車速為

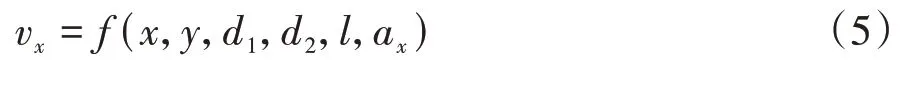
取=4.2 m，=30 m=10 m，a=4 m·s，在Matlab仿真計算得v=(，)，如圖2所示。

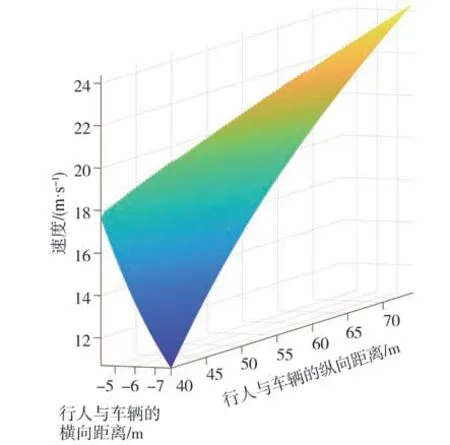
圖2 車輛與盲區內行人不碰撞時對應的最高車速

2.2 最佳安全車速

2.1 節中求得的不碰撞行人最高車速是盲區安全車速考量的重要指標，但隨著的減小，v也會逐漸減小，發生“死鎖”現象。上述模型存在以下問題：

（1）沒有考慮到盲區面積的大小，忽略盲區內行人的潛在概率；

（2）模型過于保守，將安全標準嚴格限制為車速降為零。

為解決上述問題，提高車輛通過盲區速度，利用不碰撞行人最高車速v、盲區面積變化率、城市道路限速與最低車速等因素綜合計算盲區的安全車速，構建式（6），且≤。

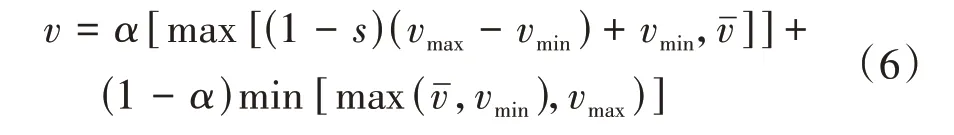
式中為盲區面積，=0.5(+)，為盲區寬度。

盲區面積變化率：

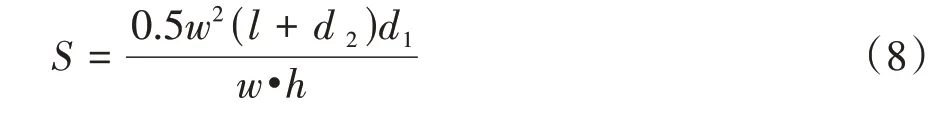
式中為預期功能起作用時的初始盲區長度，由式（9）得到。式（9）中40為車輛百公里制動距離，m。

最后調節求得最佳安全車速。

3 控制系統結構

所設計的控制系統主要由盲區緊急制動決策層、速度跟蹤控制層、執行層和傳感器組成，如圖3所示。決策層根據車輛上的傳感器不斷檢測周邊盲區的信息，包括盲區縱向長度、車輛傳感器與盲區的橫向距離和車輛傳感器與盲區的縱向距離，用于計算車輛的最佳安全車速，同時實時采集車輛當前行駛速度v、發動機轉矩和制動力矩反饋給非線性觀測器和速度控制器。控制層將決策層輸出的車輛期望速度和目標加速度經過逆縱向動力學模型轉換成期望油門開度和期望制動壓力，利用切換控制器輸出給執行層中的發動機和制動系統，以實現對期望速度的跟蹤控制。

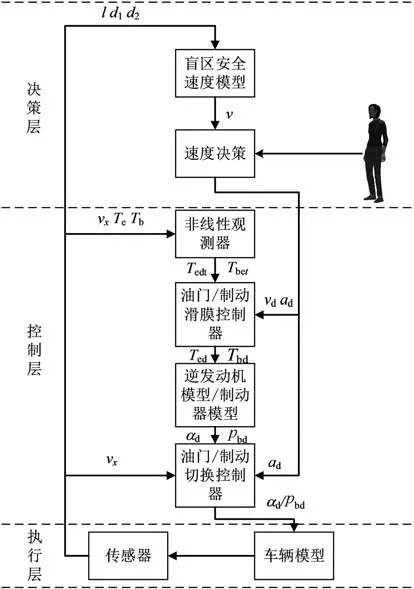
圖3 考慮預期功能安全的智能汽車自動緊急制動系統結構

4 車速跟蹤控制器設計

車輛本身是一個參數不確定的高度非線性系統，且容易受到外部干擾，本文在滑模控制器基礎上加入了非線性干擾觀測器，并設計了油門/制動切換控制器完成油門、制動器平穩切換，實現對期望安全車速的良好跟蹤。

4.1 車輛縱向動力學模型

整車縱向動力學方程為

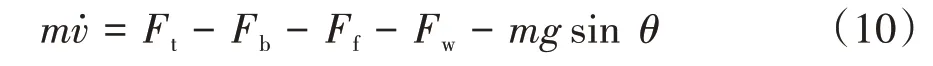
式中：為整車質量；為車速；為驅動力；為地面制動力；為滾動阻力，=sin；為空氣阻力，=；為空氣阻力系數；為重力加速度；為道路坡度；為滾動阻力系數。

車速與發動機轉速的關系為

式中：為車輪半徑；為發動機轉速；為變速器傳動比；為主減速器傳動比。

發動機轉矩與驅動力矩的關系為

式中：為發動機轉動慣量；為發動機轉矩；為驅動力矩。

聯立式（10）～式（12）得

用等效1 階慣性環節描述發動機和制動系的動態過程，發動機轉矩與油門開度和制動力矩與制動壓力之間的關系為

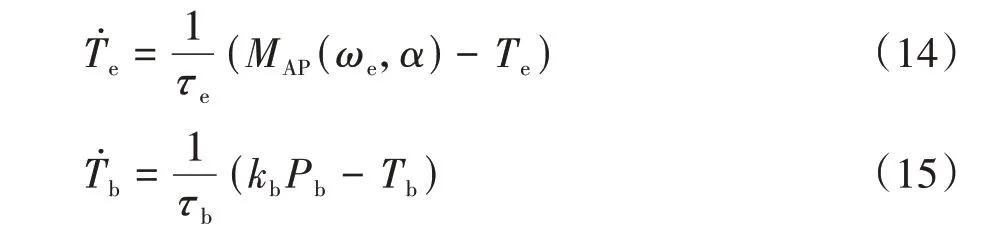
4.2 油門/制動滑模控制器

式（13）可改寫為

4.2.1 非線性干擾觀測器

定義觀測誤差為

式中：、為滑模控制器的輸出；、為非線性干擾觀測器的輸出。

4.2.2 油門滑模控制器

當采取油門控制時，制動力為0，由式（13）和式（22）得到加入非線性干擾觀測器的車輛油門控制模型為

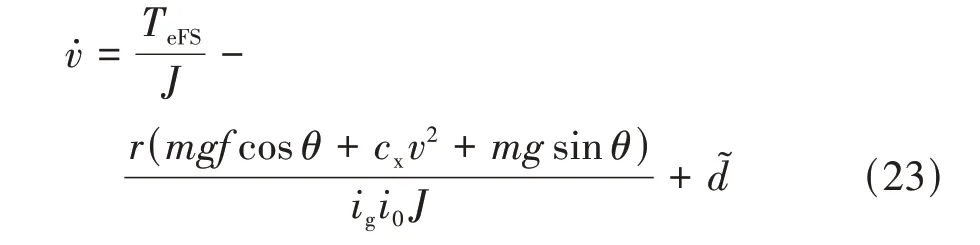
定義第1滑模面為

式中：為滑模面系數；=-。

要想達到理想的滑動模態控制，需滿足：

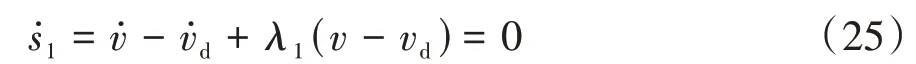
由式（23）和式（25）可得，發動機轉矩等效控制律為

采用等速趨近率，滑模變結構控制律為

式中為反饋增益系數。

則發動機期望轉矩為

定義第2滑模面為

采用等速趨近率：

式中為反饋增益系數。

由式（14）、式（29）和式（30）得期望油門開度為

4.2.3 制動滑模控制器

當采取制動控制時，驅動力矩為0，由式（13）和式（22）得加入非線性干擾觀測器的車輛制動控制模型為

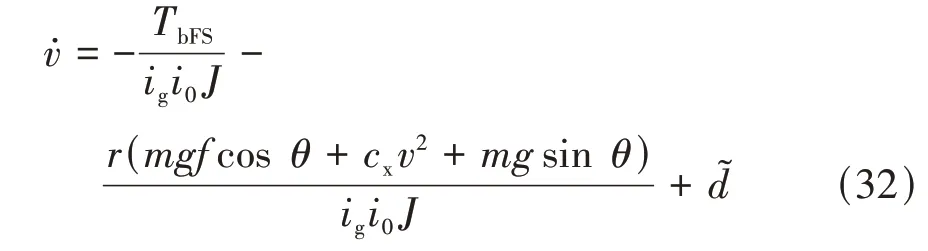
定義第3滑模面為

式中：為滑模面系數；=-。

要想達到理想的滑動模態控制，需滿足：

由式（32）和式（34）可得制動力矩等效控制律為

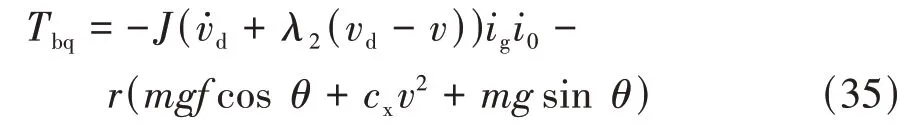
采用等速趨近率，滑模變結構控制律為

式中為反饋增益系數。

則制動期望力矩為

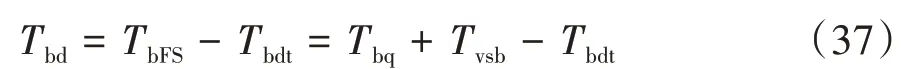
定義第4滑模面為

采用等速趨近率：

式中為反饋增益系數。

由式（15）、式（38）和式（39）得期望制動壓力為

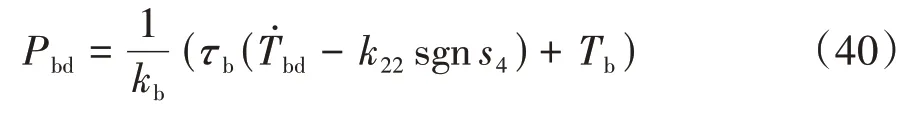
4.3 切換控制器

在進行車速跟蹤時，需要油門和制動器聯合控制實現。本文設計了節氣門/制動控制切換時的加速度基準曲線：

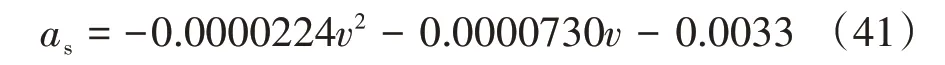
在基準加速度附近設置了切換門限，保證油門/制動較快響應的同時能平穩過渡，如表2所示。

表2 執行器切換策略

5 仿真驗證與分析

5.1 感知盲區下最佳安全車速仿真

城市中大貨車造成的盲區最為普遍，本文以此確定盲區仿真參數，如表3 所示，進行感知盲區下最佳安全車速仿真，取=0.6，結果如圖4所示。

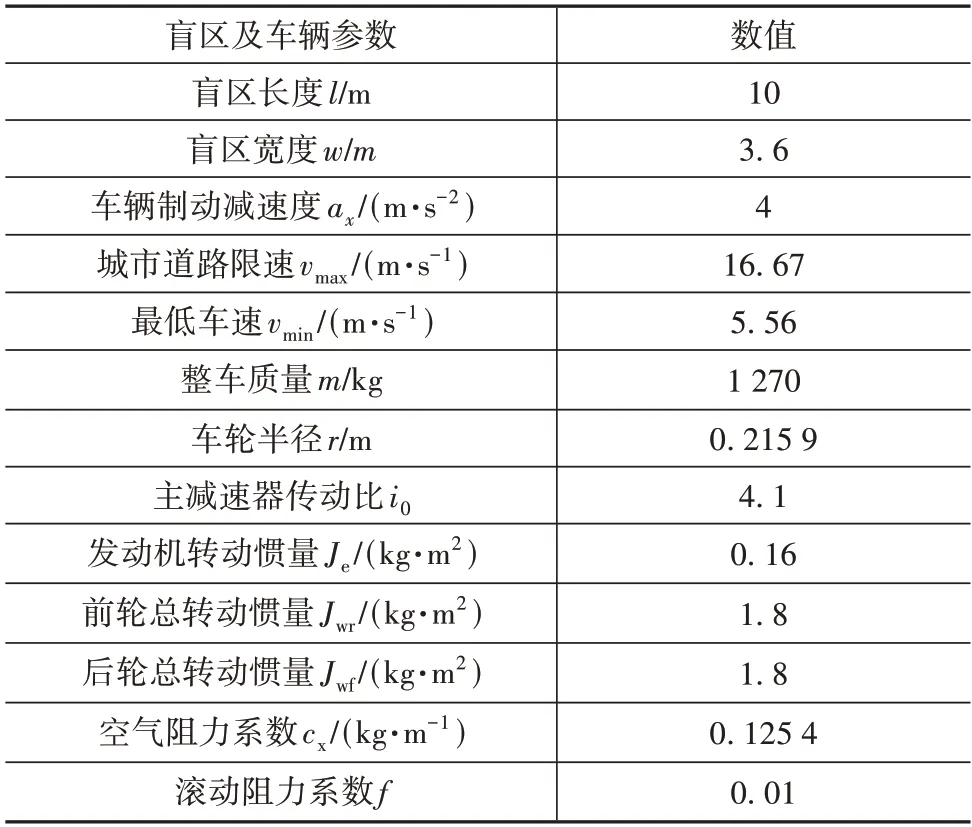
表3 仿真參數

由圖4 可見，隨著車輛傳感器與盲區的縱向距離變化，感知盲區下車輛運動可分為4個過程：

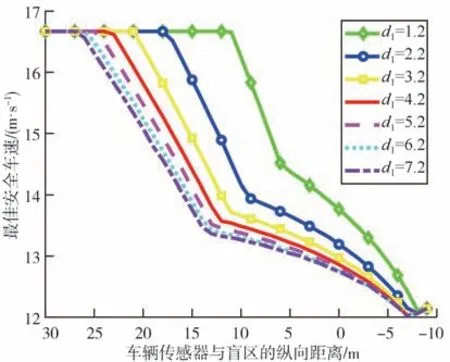
圖4 感知盲區下最佳安全車速曲線

（1）勻速運動：車輛距盲區較遠，盲區不影響車速；

（2）快減速運動：車輛進入盲區影響范圍，車速快速下降；

（3）慢減速運動：車輛進入盲區一段距離，車速下降速率開始緩慢；

（4）加速運動：車輛快駛出盲區，加速離開。

隨著傳感器與盲區的橫向距離的增大，車輛開始減速時刻會提前，車速變化也會趨緩。

5.2 感知盲區下車輛通過仿真

傳統的自動緊急制動系統由于無法感知到盲區內的潛在行人，為規避行人碰撞風險，駕駛員在遇到盲區時會采取以下兩種操作：

（1）在距離盲區一定距離時先勻減速；

（2）減速至通過盲區前達到安全車速后，保持勻速并通過盲區。

為驗證基于感知盲區下最佳安全車速的自動緊急系統的有效性，設計如下兩個試驗，取=4.2。

試驗1：為車輛設置3 種行駛策略，初始速度均設置為城市道路限速=16.67 m/s，并從同一地點出發。策略1：車輛按照盲區下最佳安全車速做減速運動；策略2：車輛以2.5 m/s減速度做勻減速運動減速至最低車速；策略3：車輛做勻速運動。車輛分別按照以上3種策略行駛，直至通過盲區。

試驗2：車輛行駛策略、初始速度和出發地點保持不變，但在距離盲區消失30 m 時，盲區區域中線處有一行人在縱向距離盲區2 m 處以1.5 m/s 速度開始橫向穿過道路，車輛在檢測到行人后做緊急制動，直至停車。

5.3 仿真結果與分析

5.3.1 快速性

圖5～圖7為試驗1下的仿真結果。

由圖5 可知，車輛在策略1 下比在策略3 下行駛通過盲區的時刻只晚0.46 s，而車輛在策略2下比在策略3 下行駛通過盲區的時刻晚了1.76 s。由圖6和圖7 可知，車輛在策略1 下比在策略3 下行駛通過盲區時落后7.64 m，車輛在策略2 下卻比在策略3下行駛通過盲區時落后了29.29 m。以上表明，按照感知盲區下最佳安全車速行駛的車輛雖然進行了減速操作，但在沒有行人時能快速通過盲區。

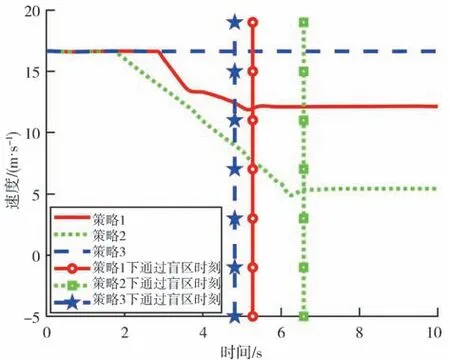
圖5 盲區內無行人車速變化圖

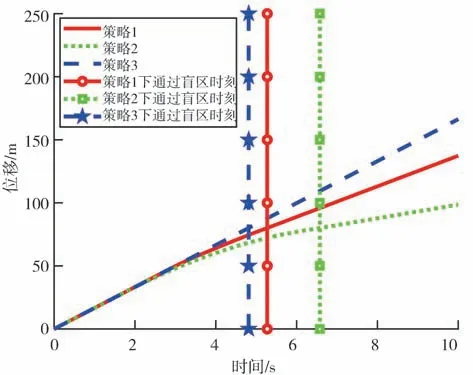
圖6 盲區內無行人通過車輛位移變化圖

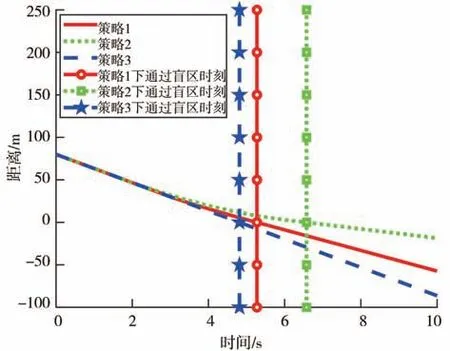
圖7 盲區內無行人通過車輛與盲區消失界限距離變化圖

5.3.2 安全性

圖8～圖10為試驗2下的仿真結果。

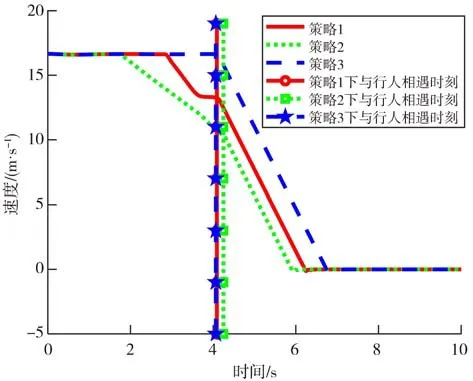
圖8 盲區內有行人通過車速變化圖

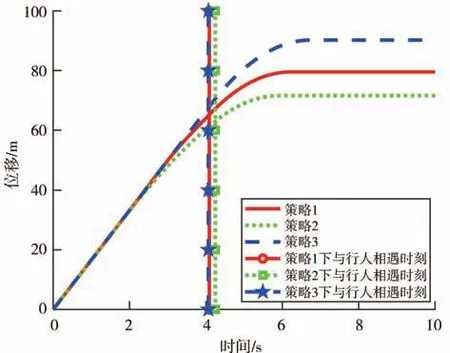
圖9 盲區內有行人通過車輛位移變化圖

圖10 盲區內有行人通過車輛與行人距離變化圖

由圖8可知，車輛在策略1、策略2和策略3下行駛分別在4.09、4.25、4.07 s后發現行人并進行緊急制動，且車輛分別在6.22、5.90、6.74 s 后速度降為零。由圖9 可知，車輛在策略1 下比在策略3 下行駛發現行人時的位移少2.38 m，比在策略2 下行駛發現行人時的位移大2.26 m。

由圖10 可知，車輛在策略3 下行駛越過了行人橫穿軌跡8.21 m，對行人造成極大威脅，而車輛在策略1 與在策略2 下行駛都能在行人橫穿馬路的軌跡前及時停住車，保證行人的安全，且車輛在策略1行駛停車時僅僅與行人橫穿軌跡距離為2.475 m，車輛在策略2 下行駛達到10.45 m。綜上可知，車輛按感知盲區下最佳安全車速曲線行駛能有效利用盲區的長度，在盡量保證行人安全的前提下，快速通過盲區。

6 硬件在環仿真臺架試驗

為進一步驗證該系統的有效性，搭建了硬件在環仿真臺架，總體方案如圖11所示。

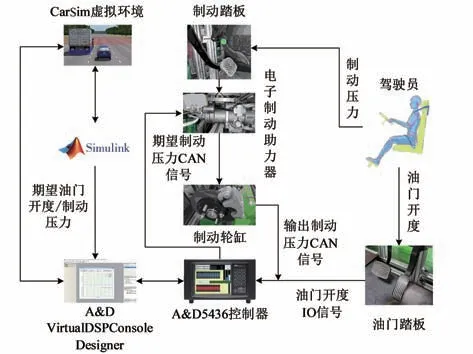
圖11 仿真臺架方案

試驗3：駕駛員控制車輛以車速16.67 m/s 勻速駛入盲區，后自動緊急制動系統介入接管車輛進行制動減速，在距離盲區消失30 m 時，盲區區域中線處一行人在縱向距離盲區2 m 處以1.5 m/s 速度開始橫向穿過道路，車輛在檢測到行人后做緊急制動，直至停車。試驗結果如圖12～圖15所示。

圖12 和圖13 表明該系統的硬件在環試驗結果與仿真結果基本保持一致，車輛能按照最佳安全車速曲線變化行駛，并能在行人橫穿軌跡前1.16 m 停車，保證了感知盲區下車輛行駛的安全性。

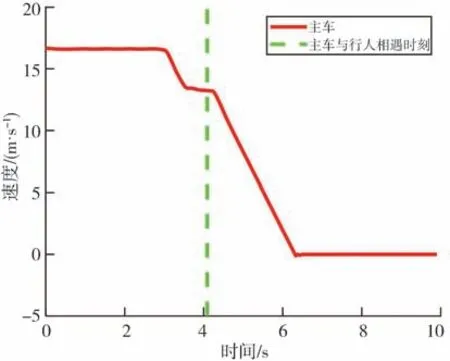
圖12 速度變化圖

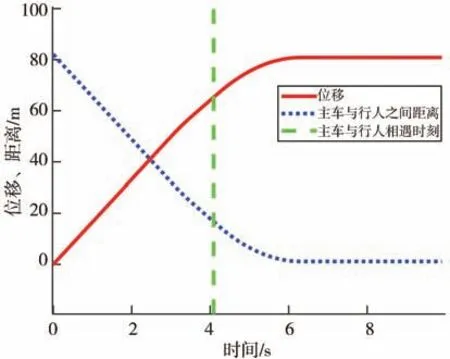
圖13 位移、距離變化圖

由圖14 可知，線控制動系統的制動壓力輸出存在0.2 s的遲滯，最終導致車輛與行人橫穿軌跡線距離較仿真結果縮短了1.315 m，但整體上對安全性影響較小。圖15 顯示在汽車遇到行人后車輛制動減速度短時間增加到0.74，超過了人體舒適加速度的極限值0.5，會讓駕駛員有短暫不適的感覺。可以通過限制緊急制動最大制動壓力來改善舒適性，但與此同時也會減低一定的安全性。

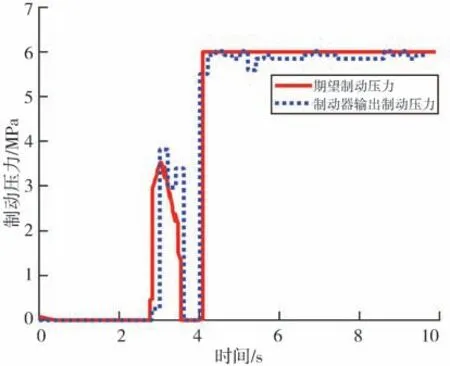
圖14 制動壓力變化圖

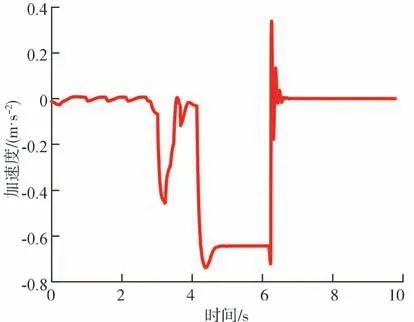
圖15 主車加速度變化圖

7 結論

（1）從考慮預期功能安全角度出發，在傳統的自動緊急制動系統上增加感知盲區場景下安全車速規劃，以保證感知盲區下車輛通過安全性；

（2）設計了基于非線性干擾觀測器的速度滑模控制器，抵抗外部干擾和車輛本身的不確定性，精確地跟蹤感知盲區場景下最佳安全車速；

（3）在CarSim 仿真平臺上開展感知盲區內無行人通過與有行人通過兩種試驗，驗證了該系統的快速性和安全性，最后搭建了硬件在環仿真臺架，進一步驗證了該制動系統的有效性。