一類復雜耦合系統的有限時間集群分析

汪楚翔 劉易成 茹立寧

(國防科技大學文理學院,長沙,410073)

1 引言

集群行為是自然界中普遍存在的一種現象. 它表示一些自驅動的個體在一定的規則下,從雜亂無章的無序狀態演化為有序的群體運動現象[1]. 最常見的群體包括鳥群、魚群、羊群以及菌群等等[2]. 由于在網絡、機器人、無人機等領域方面有重要應用[3,4],這些現象吸引了眾多學者的關注. 1995 年,Vicsek 等人總結Reynolds等人[5]的研究成果,提出了一種具體研究集群現象的離散模型,被稱為Vicsek模型[6]. 經過對Vicsek 模型的改進,Cucker 和Smale[7,8]于2007 年提出了一種新的連續模型,它可用如下系統描述:其中N為個體的數量,xi,vi分別表示第i個個體的位置和速度?ψ是一個非負,非增的函數,表示粒子i與j之間的通信權重函數,表達式為ψ(s) =,β> 0. 作者證明了當β<時,系統產生無條件集群現象?而當β≥時,在初始值滿足一定條件的情形下,系統發生集群現象.隨后,Ha等人[9]利用能量泛函法將結果進一步改進,證明了當β=時,系統也發生無條件集群現象.

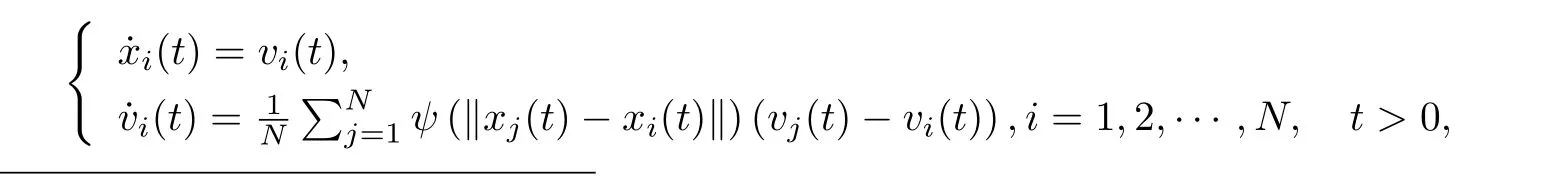
在上述研究的結果中,集群行為是在時間趨于無窮時漸近發生的,即收斂時間是長期的. 但是,研究者更關心的是能否在有限時間內系統產生集群現象. 事實上,在自然界中,魚群被捕食者撞散后,經過一段時間可再次聚集,重新形成有序的群體. 這是一種有限時間集群現象. 目前,研究此類問題的學者相對較少,具體可參見相關文獻[10–16].

在文獻[16]中,作者提出了一種擴展C S 模型,使得系統在有限時間內發生集群現象,其中通信函數ψ選取為奇異函數. 受此啟發,本文探索在非奇異通信函數影響下,這類C S 模型能否在有限時間內產生集群行為. 事實上,我們發現: 當初始值滿足一定條件時,系統將發生有限時間集群,并且收斂時間T可由個體數量N以及個體初始速度等參數決定.

本文安排如下: 在第二節,我們提出一種新的動力學系統,給出幾個引理,并對系統的解做初步估計. 在第三節中,我們利用能量泛函方法,證明在個體初始位移滿足一定條件時,系統在有限時間內發生集群行為,并進一步給出收斂時間的具體表達式. 對應的數值模擬在第四節中給出.

2 問題描述與引理

我們在d維歐氏空間中考慮一個由N個個體組成的動力學自治系統. 設xi ∈Rd,vi ∈Rd分別表示第i個個體的位置和速度,且滿足以下方程:

其中通信函數ψ定義為ψ(r)=,α>0,函數Γ:Rd →Rd表示第i個個體與第j個個體之間的速度耦合,A為正常數(用于防止個體間相撞). 對給定的v= (v1,v2,··· ,vd)∈Rd,類似文獻[10],假設Γ 滿足如下兩條性質:

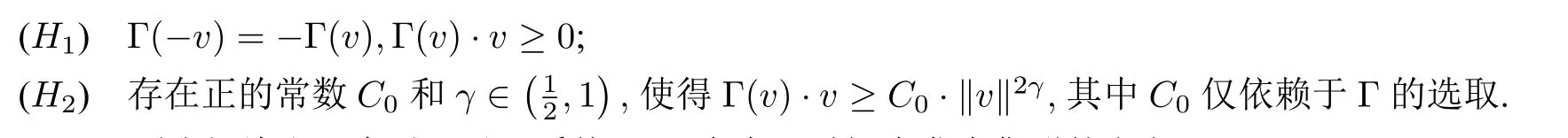
下面我們給出幾個引理以及系統(2.1)在有限時間內發生集群的定義.

引理2.1([11]) 假設函數φ滿足φ(xi,xj)=?φ(xj,xi),i,j=1,2,··· ,N,i ?=j,則

且對任意給定的y1,y2,··· ,yN,有

其中耦合函數Γ 滿足的條件與本文相同. 作者證明了當時,系統可在有限時間內發生集群. 本文將原始C S 模型與上述系統結合起來,作為一種新的推廣模型,適應范圍更加廣泛,并得出了相似的結果.

注2.3在假設(H2)中,參數γ ∈(,1)的限制可以適當放寬. 當γ ≥1 時,我們仍可得類似的結果. 由于此時引理2.4 的條件不再適用,因此集群不能在有限時間內發生,而在時間趨向于無窮時漸近達到. 作為補充,相應的結果及證明將在本文的最后給出.

定義2.1([20]) 對于任意給定的初始值{xi(0),vi(0)},i= 1,2,··· ,N, 若系統(2.1) 的解{xi(t),vi(t)}滿足以下兩個條件,則稱系統(2.1)在有限時間內發生集群:(1)所有個體速度之差在有限時間內趨于0,即

其中T1=inf{T|‖vi(t)?vj(t)‖=0,?t ≥T},稱為收斂時間?

(2)群體的直徑有界,即

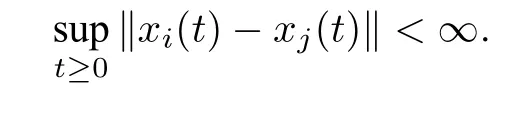
3 有限時間發生集群的條件

3.1 解的預先估計

首先,類似文獻[1–5],我們對系統(2.1)的解做出初步分析.

設x(t)=(x1(t),x2(t),··· ,xN(t)),v(t)=(v1(t),v2(t),··· ,vN(t)),

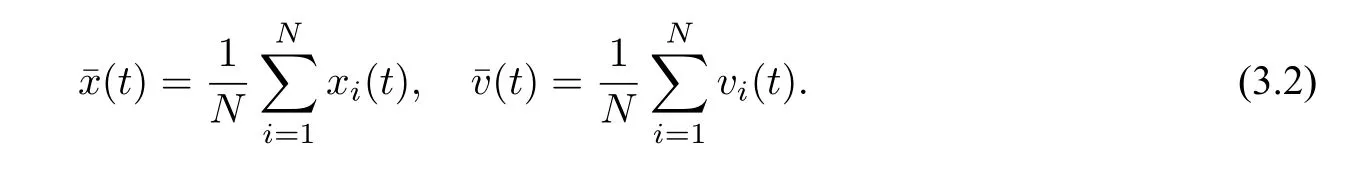
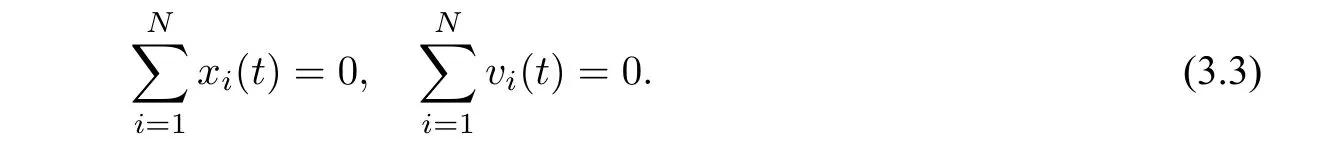
事實上,令

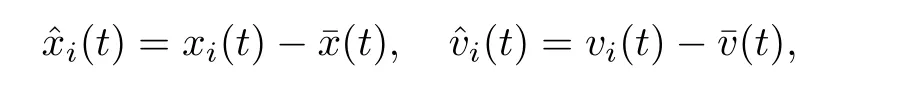
則不難驗證

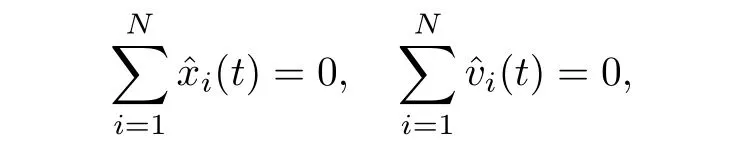
直接計算可得

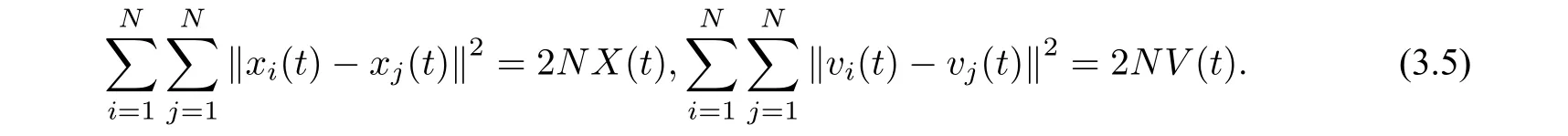
由此可知,若在有限時間內V(t)趨于0,且X(t)有界,那么定義2.1 的條件即可滿足,從而發生有限時間內集群.

我們給出如下引理:

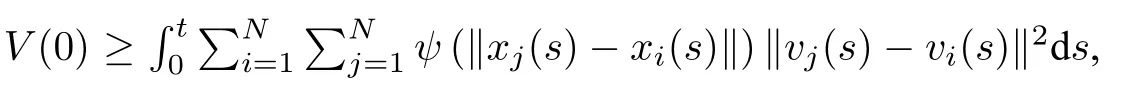
其中

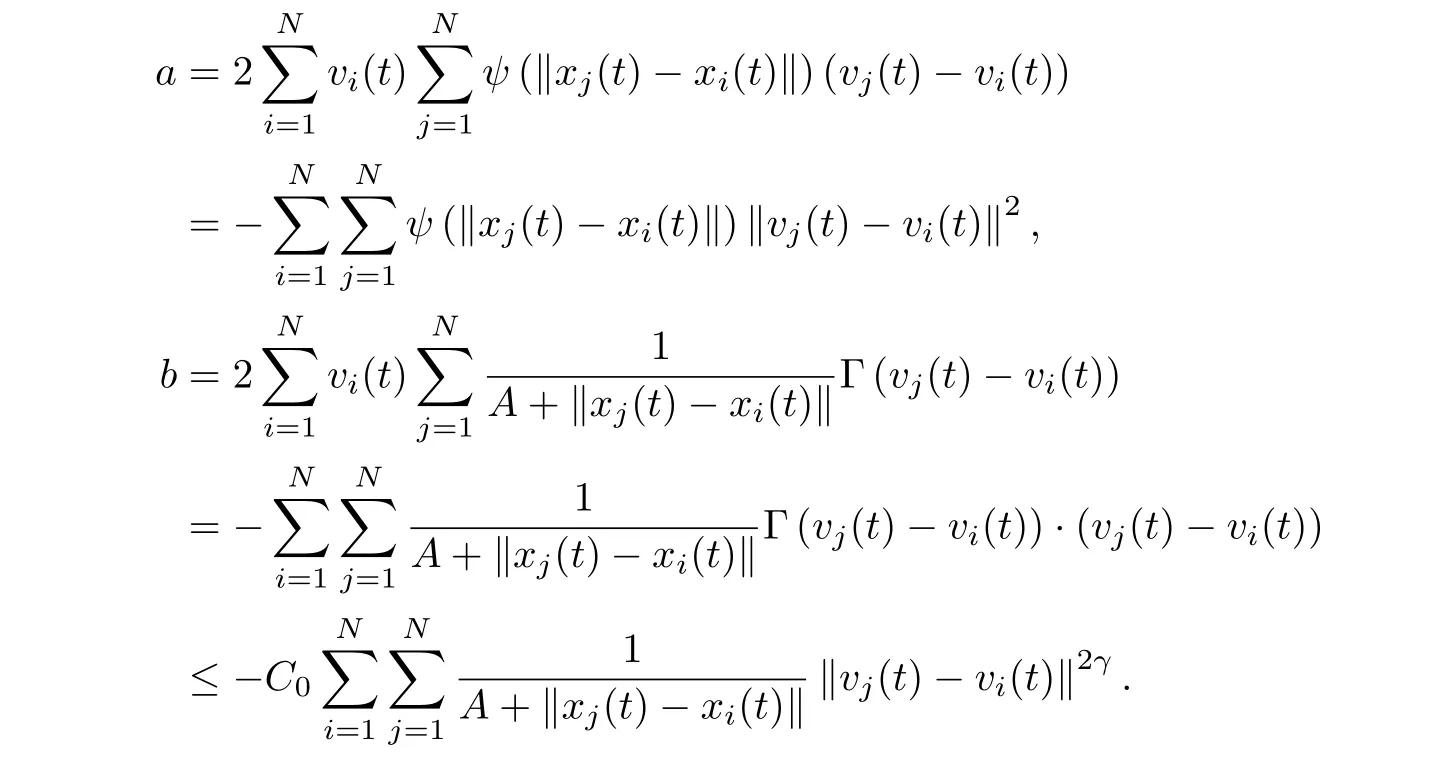
代入(3.5)式可得

兩邊對t積分,得

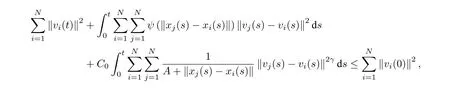
從而

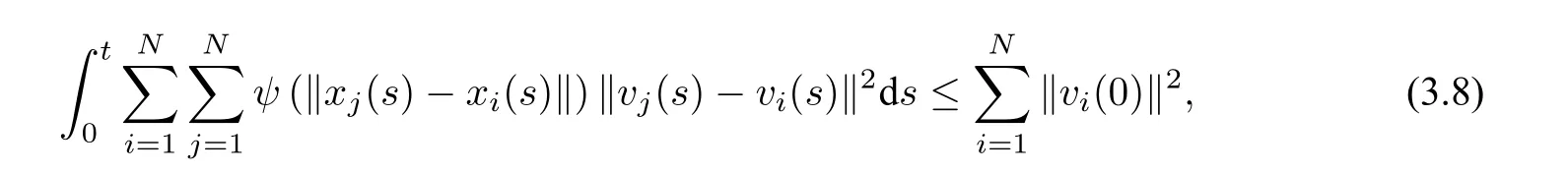
且

引理證畢.

3.2 有限時間集群

在這一節中,考慮系統(2.1)中通信函數取ψ(r) =,α> 0 的情形. 類似文獻[21]的方法,定義函數Lβ(t):

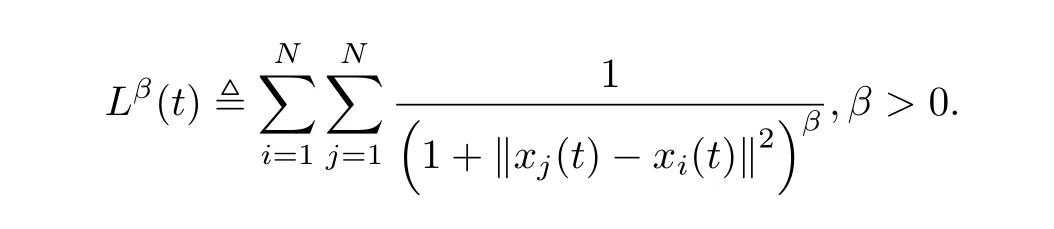
引入最大時間跨度T(x(0)):

T(x(0))?max{t ∈R+|系統(2.1)的解{(xi(t),vi(t)}在[0,t)中存在},

其依賴于初始值x(0)的選取,簡記為T0.

定理3.1假設初始值滿足‖xj(0)?xi(0)‖> 0,i,j= 1,2,··· ,N,i ?=j,則對系統(2.1)的解{xi(t),vi(t)},t ≥0,有:

當α=1 時,

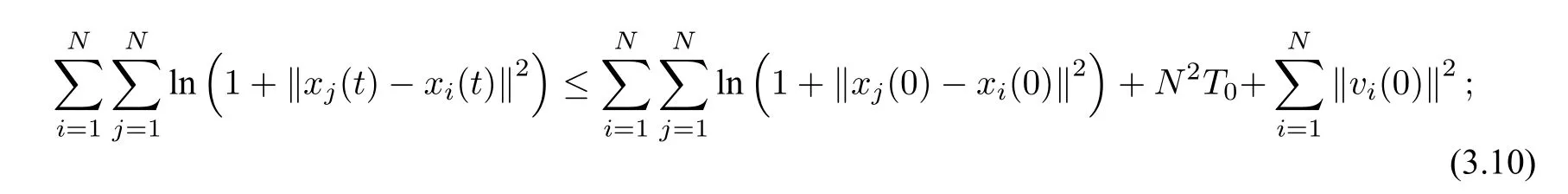
當α>1 時,

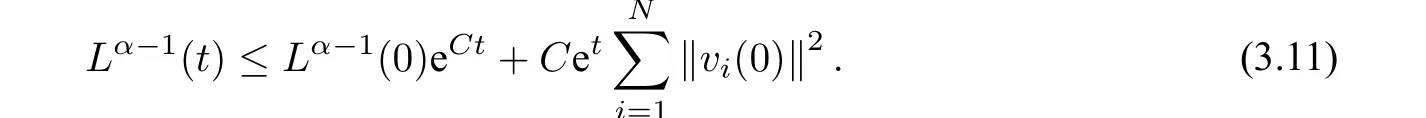
證明當α=1 時,

對t ∈[0,T0),兩邊積分可得

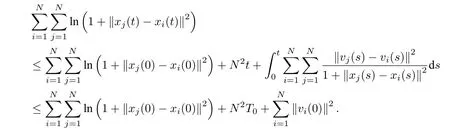
當α>1 時,直接計算可知(C為常數,不同等式中可能不相同):

對t ∈[0,T0),利用Gronwall 不等式,得到

令α=β ?1,可得

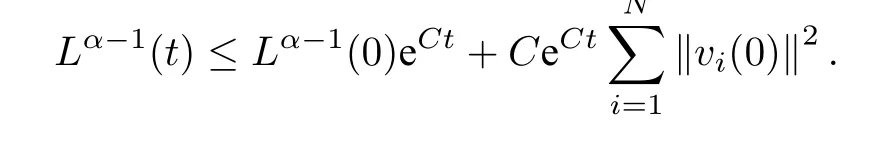
定理證畢.

定理3.2假設α ≥1,初始值滿足‖xj(0)?xi(0)‖> 0,i,j= 1,2,··· ,N,i ?=j,則系統(2.1)能在有限時間內發生集群,收斂時間T為

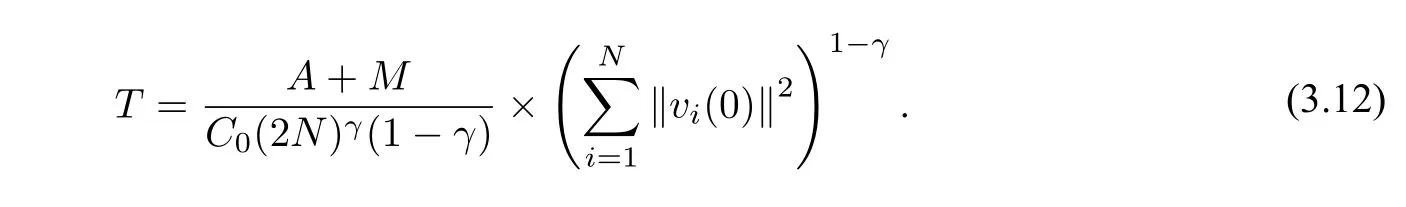
證明根據定理3.1,‖xj(t)?xi(t)‖有上界,即存在正的常數M使得

進而可得

由引理2.4 可知

其中

在(3.5)式中對t積分,可得

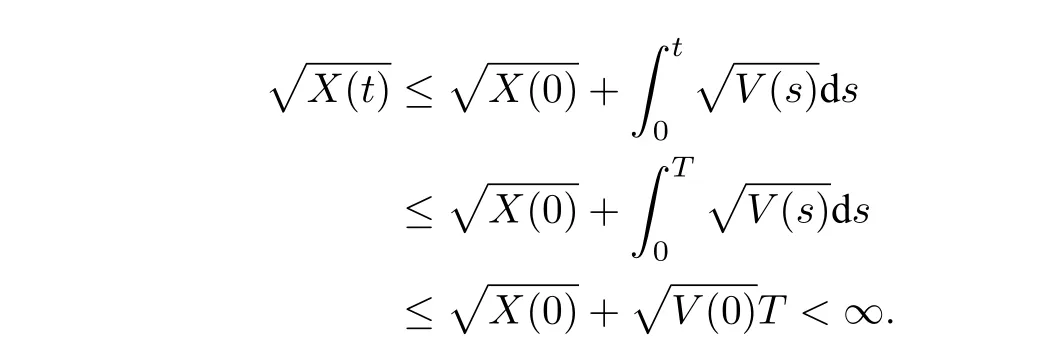
根據定義1,定理證畢.

定理3.3設γ ≥1,α ≥1,初始值滿足‖xj(0)?xi(0)‖> 0,i,j= 1,2,··· ,N,i ?=j,則系統(2.1)發生漸近集群,即收斂時間T無界.

證明與定理3.2 證明過程類似,可知

情形1γ=1. 上式化簡為

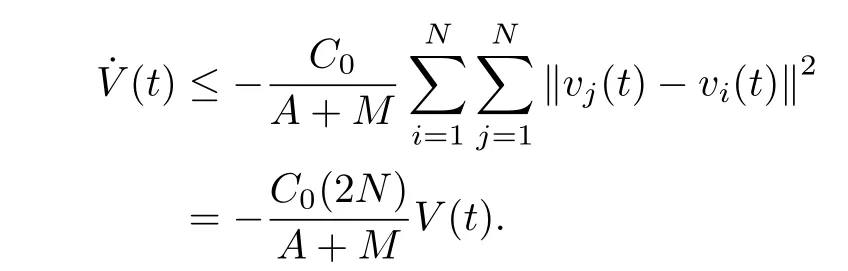
根據引理2.5,T可取為∞,即收斂時間無界,且

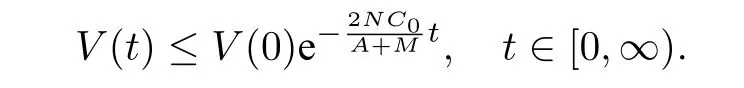
情形2γ>1. 由引理3 易得

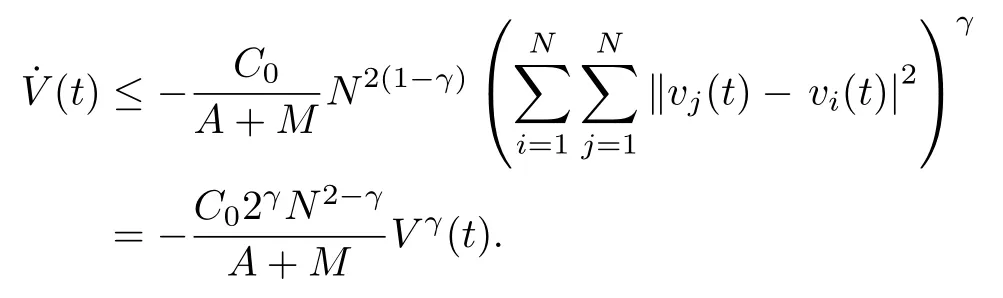
根據引理2.5,T可取為∞,即收斂時間無界,且

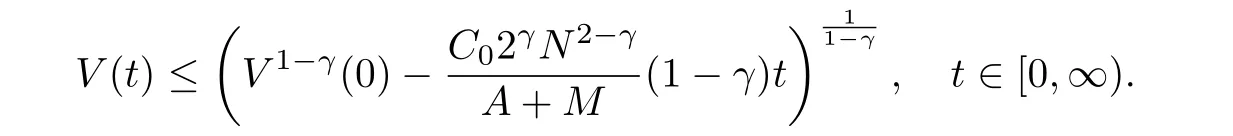
定理得證.

4 數值模擬

本節選取具體的參數值進行數值模擬,驗證本文主要結果. 取A= 1,C0= 1,Δt= 0.01,個體的初始位移與速度分別在0 到200 之間,0 到10 之間隨機取值,其余參數的取值見以下各例.

例1 取α= 1,γ= 0.55,N= 10,仿真結果在圖1 中給出. 圖1(左)表明每個個體的速度,經過t=10s 左右,速度差已經趨于零. 圖1(右)表明各個個體之間位移差的最大值,經過短暫的波動以后,在10s 左右也趨于穩定.此外,根據(3.11)式,收斂時間T=204.96s. 這些數值結果有效驗證了定理3.2 的結果.

為了突出速度耦合函數與收斂時間的關系,現在改變γ的值,其它參數保持不變,見圖2 和圖3.

例2 取α= 1,N= 10,分別取γ= 0.75,γ= 0.95. 仿真結果分別在圖2 和圖3 中給出. 圖2(左)、圖3(左)表示每個個體的速度,可以看出時間相比圖1 明顯變長,尤其是圖3(左),速度在經過t= 20s 左右之后才達到平衡.圖2(右)、圖3(右)則顯示個體的最大位移差稍有增加,同樣在相應的時間穩定下來.根據(3.11)式,收斂時間分別為T=98.27s,T=131.25s,仍符合定理3.2 的結果.

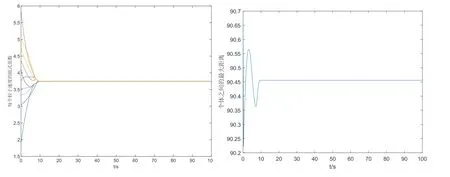
圖1 α=1,γ =0.55,N =10,收斂時間T =204.96s,同時個體之間的最大位移差有界

圖2 α=1,N =10,γ =0.75,收斂時間T =98.27s,同時個體之間的最大位移差有界

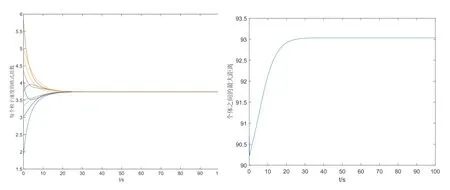
圖3 α=1,N =10,γ =0.95,收斂時間T =131.25s,同時個體之間的最大位移差有界

下例將改變個體數量,同時取不同的γ,并觀察相應結果,見圖4,圖5 和圖6.

例3 取N= 50,其余參數如上兩例,仿真結果在圖4,圖5 和圖6 中給出. 不難發現,個體數量顯著增加以后,收斂時間也相應增加(在相同的γ下),同時收斂的速度有所下降?個體最大位移差先是有所下降,然后重新上升,最后達到平衡.另一方面,從收斂時間的表達式我們也能看出,指數γ對收斂時間的影響應大于個體數量N.

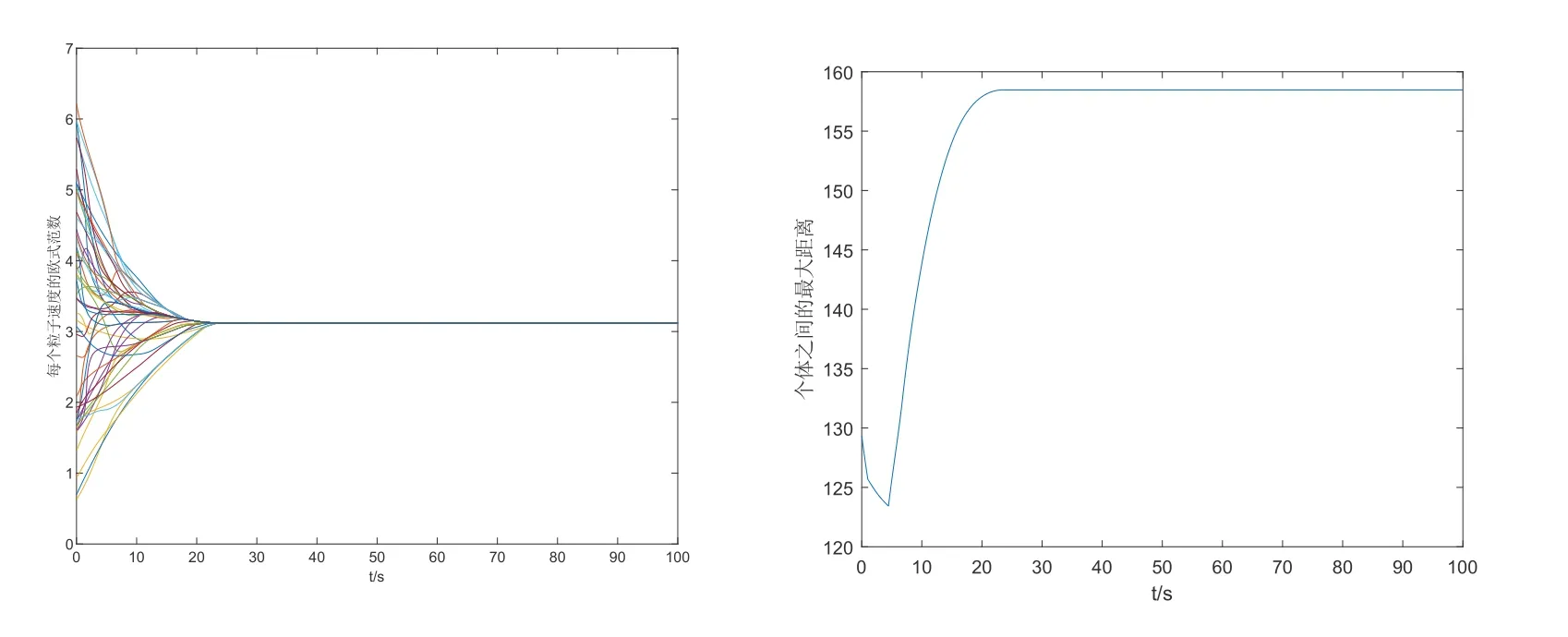
圖4 α=1,N =50,γ =0.55,收斂時間T =283.07s,同時個體之間的最大位移差有界

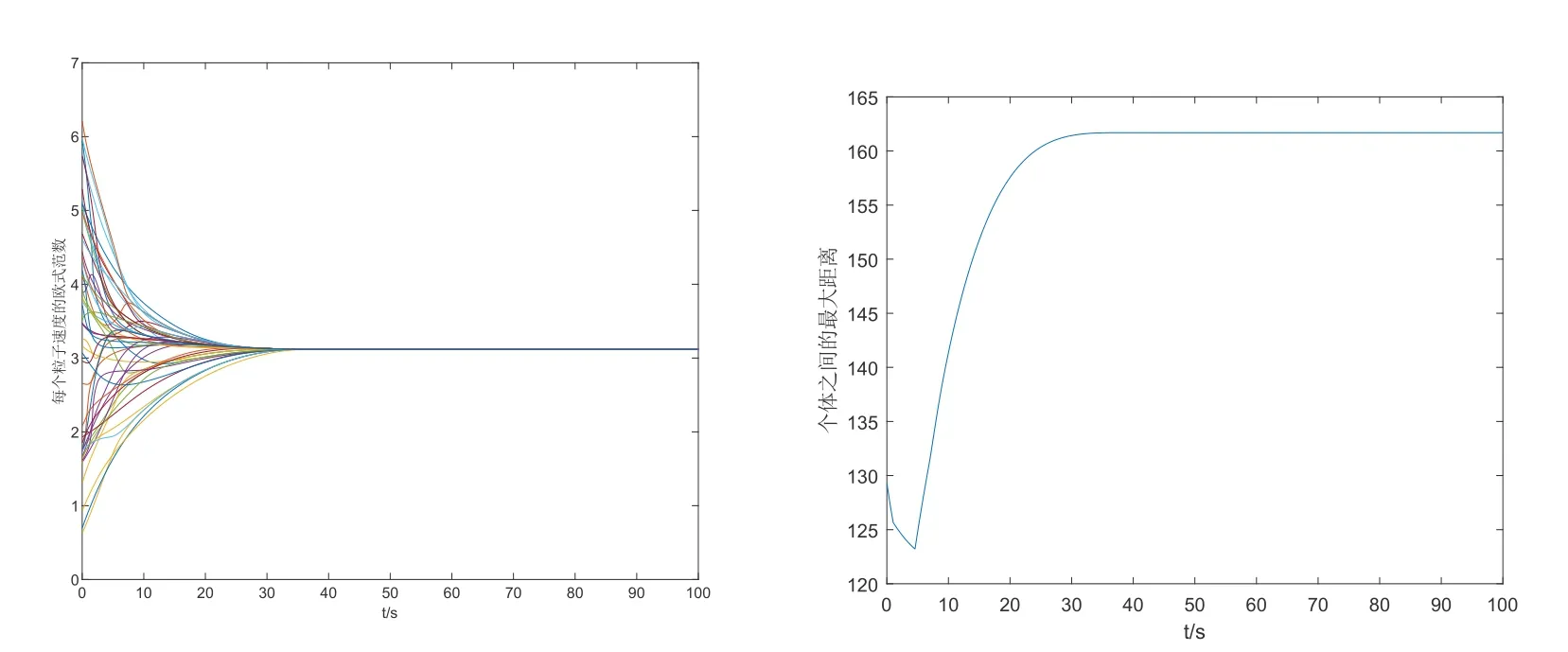
圖5 α=1,N =50,γ =0.75,收斂時間T =105.97s,同時個體之間的最大位移差有界

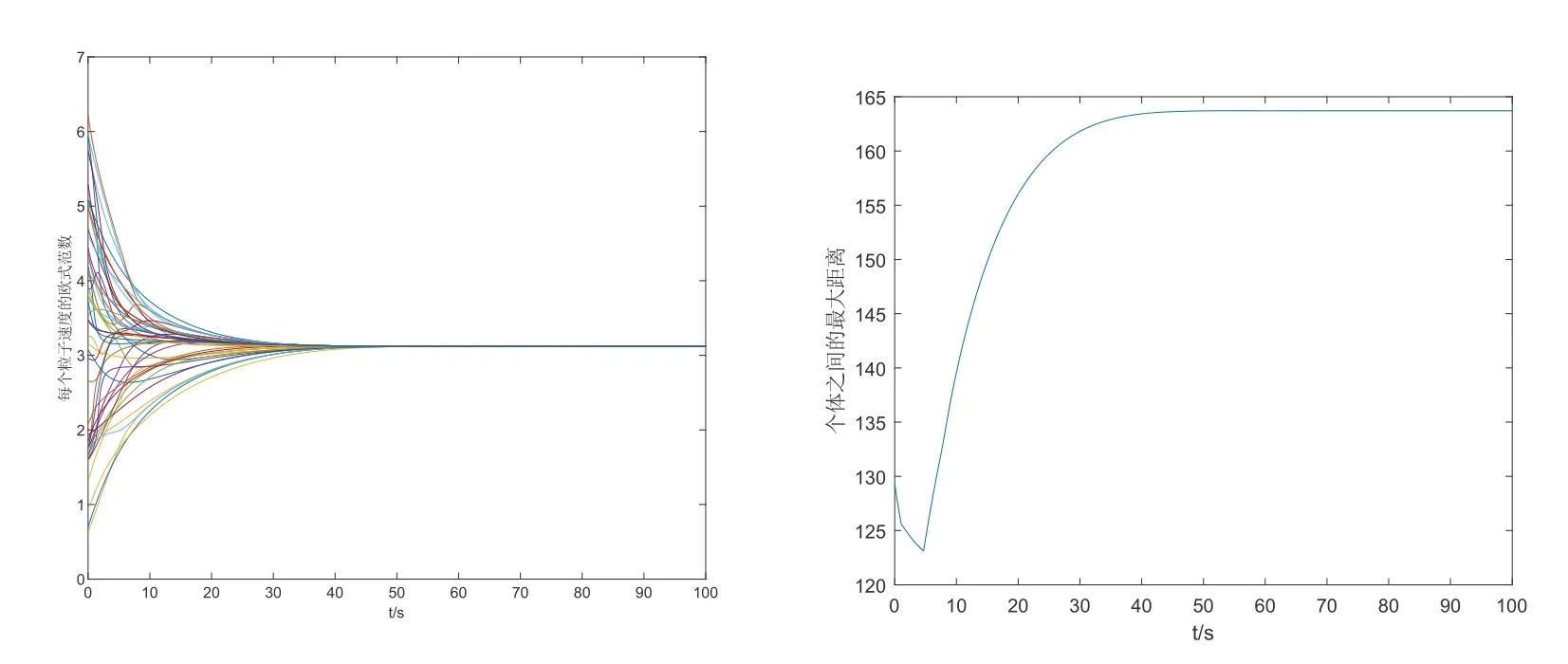
圖6 α=1,N =50,γ =0.95,收斂時間T =91.35s,同時個體之間的最大位移差有界