配網工程中數據挖掘模型的模糊聚類算法研究

顧 虹，楊 波，張 璐，潘行健，林子滟

（國網浙江德清縣供電有限公司，浙江湖州 313200）

配網工程是構建電網的重要部分，也是直接與廣大用戶相連接的末端服務管理部分[1]。合理利用內部審計來強化配網工程項目精益化管理，是規范生產經營管理的主要方式之一[2]。而隨著電網審計管理精度的提升，傳統模式已無法滿足當前配網工程數據處理控制的需求，故需及時更新數據管理技術以提高工作效率[3]。

模糊聚類算法是數據挖掘模型中的常用算法，其中使用最為廣泛的為k 均值聚類(k-means)算法[4]與模糊c 均值法[5-6]，二者主要通過對比不同集群的相似度來實現數據分析。當前，大部分數據挖掘聚類算法均是基于對象間的差異函數來進行聚類的[7-8]。然而，若考慮研究對象的屬性變量再進行聚類，可獲得更多的聚類信息。

可同時構造被指定對象與其屬性變量到同質塊最優劃分的聚類算法，這種聚類算法被稱為塊聚類。其數據處理過程用來構造一個數據矩陣，其中I是行中n個對象的集合，J是列中m個屬性變量的集合。然后將集合I分成s簇，再把集合J分成t簇。

塊聚類算法的原理是通過重新排列s×t同質塊中的行和列，找到數據矩陣的概要。研究員Duffy 與Quiroz[9]首次提出了該種聚類算法方式，并將其命名為塊聚類；而Govaert 及Nadif[10]在此基礎上設計了一種基于塊混合模型的塊分類期望最大化（Expection Maximization，EM）算法（塊CEM）；之后又研究了基于模糊c 均值劃分的塊模糊c 均值法（塊FCM）[11]。文中基于模糊k 均值方法提出了塊模糊k 值（塊FKM）算法。

1 塊模糊聚類算法

聚類分析中的一項重要技術是聚類混合[12]，在考慮塊CEM 算法之前，需先引入一個塊混合模型。假設數據集X=(x1,…,xn)是由混合分布生成，則：

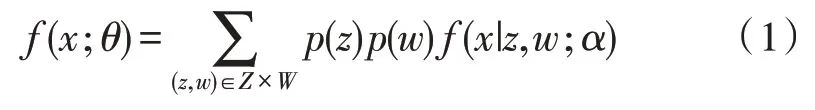
其中，Z是集合I到s簇的劃分，W是集合J到t簇的劃分。α是概率密度函數的一個參數，其目標是找到一個最優的分區對(z，w)。設xi是從第k個簇抽樣的向量，則其概率密度函數是確定的。同時由于zi與wj固定后的隨機變量是獨立的，因此樣本X的概率密度函數可表示為：

從而獲得塊混合模型為：

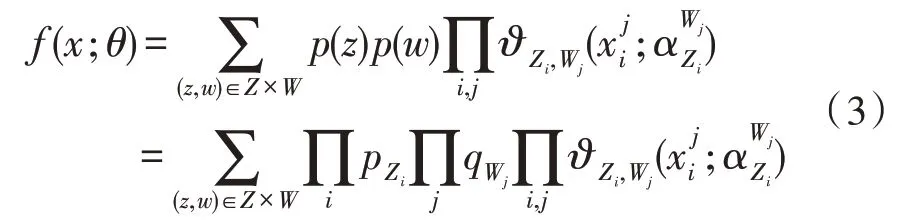
由z、w、可生成一個數據集X。為了同時處理數據與屬性變量的劃分，需要完成對數似然準則f(X；θ)的顯性表達式。所以使用分類似然法[13]，通過最大化以下分類對數似然函數提出了區塊CEM：

對于最大化分類對數似然函數Lc(z,w;θ)，首先需確定w和q的參數值，然后再確定參數z與p。當w及q固定時，對數似然函數Lc(z,w;θ)可表示為：

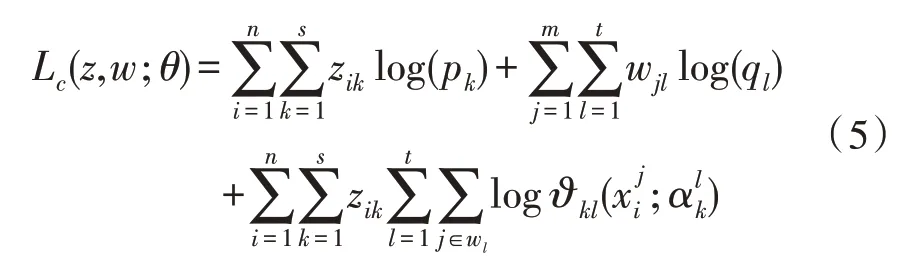
求解z固定的完全最大似然函數Lc(z,w;θ)就相當于最大化Lc(z,θ|w)，故可通過應用于混合模型的CEM 算法來實現。算法的具體步驟如下：

1）令r=1，2 ≤s≤n，2 ≤t≤m，并給出初始值z(0)、w(0)和θ(0)。

2）由z(r)、w(r)、θ(r)計算z(r+1)、w(r+1)、θ(r+1)：

①從z(r)、p(r)及α(r)中得到數據(u1,…,un)，采用CEM 計算z(r+1)、p(r+1)和α(r)；

②從w(r)、q(r)、α(r)中獲取數據(v1,…,vm)，且使用CEM 計算w(r+1)、q(r+1)和α(r+1)。

3）重復步驟2），直至數據收斂。

2 改進數據挖掘模型模糊聚類算法

2.1 塊模糊c均值法

自從Ruspini[14]在聚類中使用模糊c 均值劃分以來，模糊聚類得到了廣泛的研究與應用。基于塊混合模型及模糊c 均值劃分，Govaert 與Nadif 提出了塊FCM 作為一種新的塊聚類方法，塊混合模型可以表示為：

其中，θ=(p,q,α)。而Hathaway[15]對EM 做出了另一種解釋：

式（7）中，c與d分別表示觀測值及屬性的模糊劃分。Govaert 和Nadif 擴展了上述函數，提出了具有以下目標函數的塊模糊c 均值方法（塊FCM）：

假設概率密度函數?kl為一個充分統計的實值函數所定義的量[15]。則式（8）可表示為：

當d和q固定時，有：

固定d與q后，最大化Fc(c,d,θ) 等效于最大化Fc(c,θ|d)。則該準則的最大化可被視為與經典混合模型相關聯對數似然函數最大化的EM算法，當c和p固定時，同樣可獲得：

Fc(d,θ|c)的最大化可視為應用于經典混合模型的EM 算法，因此能將塊FCM 算法總結如下：

1）令r=1，2 ≤s≤n，2 ≤t≤m，并給出初始值c、d和θ。

2）由c(r)、d(r)、θ(r))計算c(r+1)、d(r+1)、θ(r+1)：

①從c(r)、p(r)與α(r)中獲取數據(u1,…,un)，并使用EM 計算c(r+1)、p(r+1)及α(r+0.5)；

②從d(r)、q(r)、α(r+0.5)中得到數據(v1,…,vm)，再使用EM 計算d(r+1)、q(r+1)和α(r+0.5)。

3）重復步驟2），直至數據收斂。

2.2 塊模糊k值法

令Y={y1,…,yI}為一組待分類數據，使每個數據均由一組A1,…,AJ屬性進行定義。而屬性Aj描述了由表示的值域，其中Lj是屬性Aj的類別數。假設vk=(vk1,…,vkJ)是第k個星系團的質心，每個分量vkj=(vkj1,…,vkjLj)，k=1,…,K，j=1,…,J。則Sadjad 使用了以下公式來匹配相異測度：

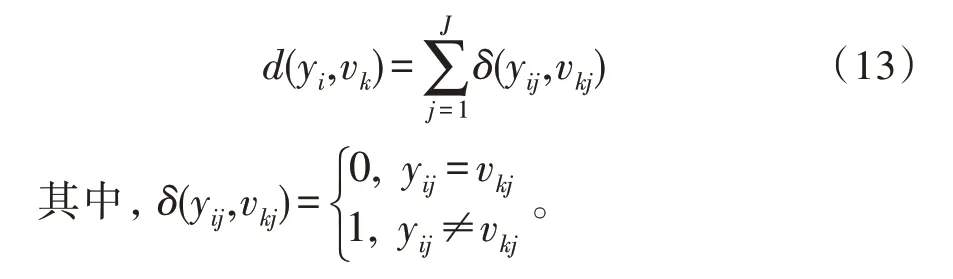
隨后，引入模糊k 值模式分塊聚類的概念，并提出塊FKM 模型。塊FKM 聚類算法旨在最小化以下目標函數：

式（15）中，若j=1,…,k，有；而當t=1,…,l，則有。X是具有n個觀測值和d種屬性的數據組，Y則是X的轉置。

對于m1＞1、m2＞1、μij∈[0,1]、σij∈[0,1]，塊FKM的更新公式如下：

塊FKM 算法步驟如下：

1）令r=1，ε＞0，2 ≤k≤n，2 ≤l≤d，且給出初始值μ(0)、σ(0)；

2）由μ(r-1)、σ(r-1)、v(r-1)和w(r-1)計算出μ(r)、σ(r)、v(r)和w(r)；

3）比較μ(r)、σ(r)和μ(r-1)、σ(r-1)，若‖μ(r)-μ(r-1)‖+‖σ(r)-σ(r-1)‖＜ε，則停止；否則，令r=r+1，并返回步驟2）。

3 算法實驗結果

3.1 案例一

利用真實工程數據給出的部分數值及數據集進行實驗，原始數據集具有10 個觀察值及9 個屬性，具體如圖1 所示。塊FKM 與塊FCM 均將數據集分類為如圖2 所示的數據集，且分塊結果一致。

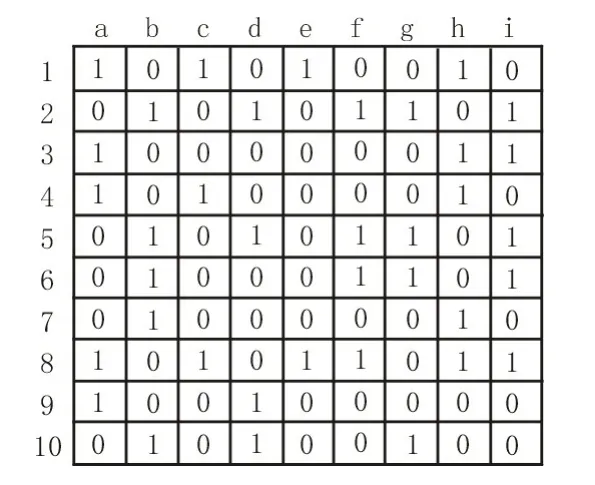
圖1 原始數據集

圖2 塊變換修正后的數據集

經過計算迭代次數的平均值，發現FKM 區塊的平均凈指數約為5 倍，而FCM 區塊的平均凈指數超過20 倍。對比可知，未經模糊算法優化的CEM 分類值效率更低。因此，所提出的改進k 值塊模糊算法FKM 比c 值塊模糊算法FCM 更節省時間。

3.2 案例二

為比較FKM 塊與FCM 塊在進行類別區分時的準確性，對配網工程成本數據進行了簡單的分類。即將其分為直接材料成本、直接人工成本、變動制造費用成本及固定制造費用成本。將101 個成本實例代入模型進行聚類，再將聚類數固定為4，來分別實現這兩個算法。為了對比分析文中提出的改進k 均值塊模糊算法的效果，采用了2 類和4 類兩種不同屬性的聚類數。

表1 列出了配網工程承包數據集屬性聚類結果，并解釋了兩種算法對屬性2 及屬性4 的聚類結果。從對成本類別的聚類結果可以看出，塊FKM 的精度顯著高于塊FCM。且在實例的聚類中，屬性的聚類數越大，特征越穩定[16-17]。

表1 配網工程成本數據集屬性聚類結果

4 結束語

文中提出了改進k 均值塊模糊算法FKM，其可同時構造聚類對象并進行屬性變量到同構塊的最優劃分。將所提出的區塊FKM 與區塊FCM 的數值數據集和真實數據集進行了比較。實驗與對比分析結果表明，該方法具有較好的準確性及有效性。

在配網工程中深度應用海量數據并構建多種類別的數據高效處理模型時，仍需注意以下幾個方面：1）動態獲取主要數據，建立數據信息變化感知機制；2）基于歷年工程海量數據的信息挖掘結果，深度分析數據走向趨勢；3）綜合利用數據感知模塊，構建新型數據挖掘模糊聚類體系。最終融合嵌入投資預算編報鏈路打造“流程閉環、共建共享”的基建工程內控機制，從而創新拓展建設成果，構建配網工程數據挖掘體系應用。