基于剛度比值的頂升糾傾整體結構受力性能

岳慶霞， 沈振錕

(山東建筑大學 a.土木工程學院;b.建筑結構加固改造與地下空間工程教育部重點實驗室，濟南 250101)

0 引 言

由于勘察、設計、施工、使用維護不當及自然災害等原因，建筑物地基會產生不均勻沉降，導致建筑物傾斜，影響其安全使用。對整體性能較好的建筑物進行糾傾處理，可避免建筑物拆除造成的經濟浪費和環境污染，特別是在歷史建筑或文物建筑保護方面，社會效益更為顯著。

建筑物糾傾方法總體可以分為3種：頂升法、迫降法和頂升與迫降綜合法。迫降法應用最廣泛,但不適用于對建筑物底層標高有特別要求、建筑物傾斜斜率較大和基礎形式為樁基礎的結構。頂升糾傾法在建筑物底部安放托換結構，將上部結構截斷，在托換結構底部設置千斤頂，以新增或原有承臺作為反力體系將建筑物頂升，從而達到糾傾的目的。

頂升糾傾法的關鍵是托換結構、頂升裝置及其控制體系的設置。四面包裹式托換結構安全度高、性能良好，在實際工程中應用廣泛，許多學者針對托換節點的受力性能展開研究。杜健民等在試驗基礎上進行理論分析，將托換節點的破壞過程分為滑移前和滑移后2個階段，并分別提出托換結構抗沖剪承載力的預測模型和設計建議。都愛華等針對界面沖切滑移前這一階段，提出框架柱四面托換節點的空間“拉桿拱”力學模型，并推導出框架柱托換節點承載力的理論計算公式。張鑫等進行16個四面包裹式托換節點的試驗研究，通過回歸分析并結合工程實踐，提出托換梁承載力的計算公式，該式被納入《建(構)筑物移位工程技術規程》(GJ/T 239—2011)。岳慶霞等對配置不同界面鋼筋的14組托換節點進行試驗研究，提出考慮界面鋼筋的摩擦剪切公式，并提出拉-壓桿計算模型，推導得到托換梁受剪承載力計算公式，可以根據托換梁的受剪承載力及界面承載力計算公式確定界面鋼筋的配量，優化托換節點的設計。

現有的研究大多針對建筑物平移工程中單個托換節點的受力特點和承載力，并逐漸形成托換結構的設計計算方法，而針對建筑物頂升糾傾托換結構的研究較少，實際工程設計時一般參考平移托換結構的設計方法。但是,建筑物頂升糾傾托換與平移托換有所不同。建筑物平移托換時，建筑各點在豎向沒有相對位移，可以進行單個托換節點的受力性能研究，而建筑物頂升糾傾托換時，托換節點之間承受不同的豎向位移，各托換節點之間通過連梁發生相互作用，托換結構與上部結構要協同受力和變形，因此在頂升糾傾工程中，托換結構的設計需要在考慮自身整體剛度的同時考慮托換結構與上部結構的共同作用，二者之間剛度要協調。

本文考慮上部結構與托換結構剛度的比值，通過理論計算與Abaqus有限元模擬，分析不同剛度比值情況下上部結構的受力與變形特征，從而給出托換結構與上部結構剛度比值的建議值，為建筑物頂升糾傾托換結構的設計提供參考。

1 算例概況

1.1 框架結構設計

以一個典型框架結構為頂升糾傾研究對象，對其進行結構設計。框架結構整體共6層，橫向為5跨、柱距為7.2 m，縱向為3跨、柱距為6.0 m，結構平面布置示意見圖1。

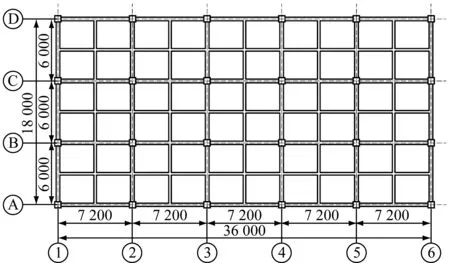
圖 1 框架結構平面布置示意,mm

框架設計層高為3.6 m，結構整體采用C30混凝土和HRB400鋼筋。框架柱截面為600 mm×600 mm，框架梁截面為350 mm×750 mm，次梁截面為250 mm×550 mm，板厚為120 mm。載荷參考國家標準《建筑結構荷載規范》(GB 50009—2012)，活載荷取2.0 kN/m，風載荷取1.2 kN/m，不考慮地震作用。運用PKPM結構設計軟件進行結構配筋設計，梁柱截面配筋見圖2。

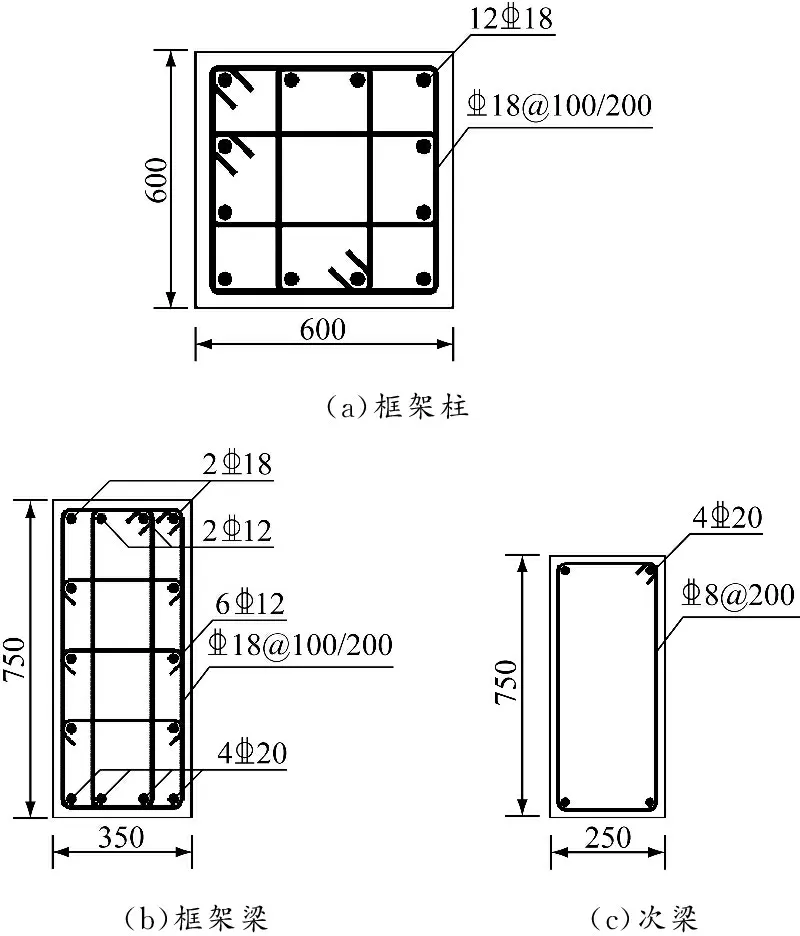
圖 2 框架梁柱截面配筋,mm

1.2 托換結構設計

針對該框架結構進行頂升糾傾托換結構設計，柱下托換節點采用廣泛應用的四面包裹式托換節點，托換節點設計根據《建(構)筑物移位工程技術規程》(JGJ/T 239—2011)進行設計，框架柱柱底軸力分布見表1。

表 1 框架柱柱底軸力分布 kN

柱底最大軸力為2 387.9 kN，以此軸力為托換節點承載力設計值，認為四周托換梁共同分擔柱底軸力，框架柱托換節點設計見圖3。

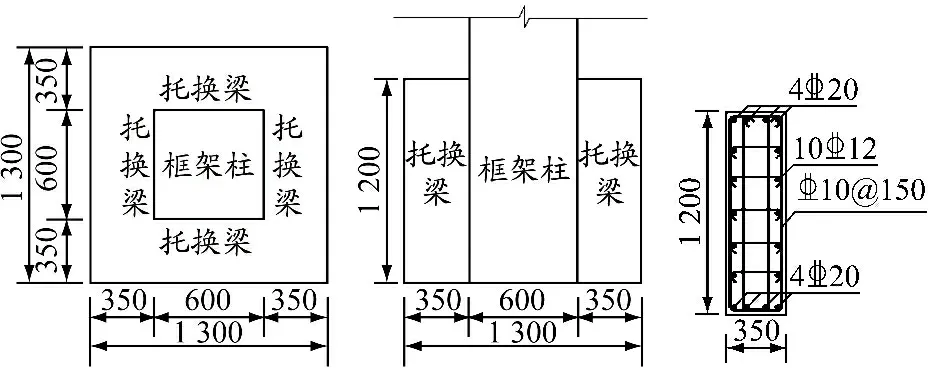
圖 3 托換節點設計,mm

托換節點間的連梁寬度設計為300 mm，選取連梁高度作為對照變量，通過改變連梁高度改變托換結構整體剛度，梁高分別取300、400、500、600和700 mm，均按照滿足構造配筋進行設計，連梁截面配筋見圖4(其中箍筋直徑均為8 mm、間距為200 mm)，托換結構整體平面示意見圖5。

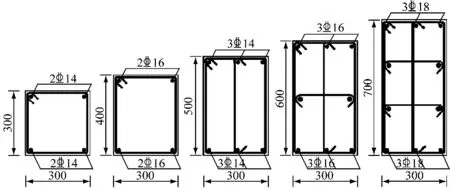
圖 4 連梁截面配筋設計,mm

圖 5 托換結構平面示意,mm

2 結構豎向剛度計算

2.1 框架結構剛度

框架結構水平剛度的計算較為成熟，但豎向剛度的計算公式較少。孫澄潮等認為框架結構的豎向剛度主要由框架梁的抗剪剛度提供，同時考慮節點轉角的影響系數和上部結構豎向剛度的貢獻衰減系數，計算示意見圖6，得到框架結構的豎向剛度計算公式為

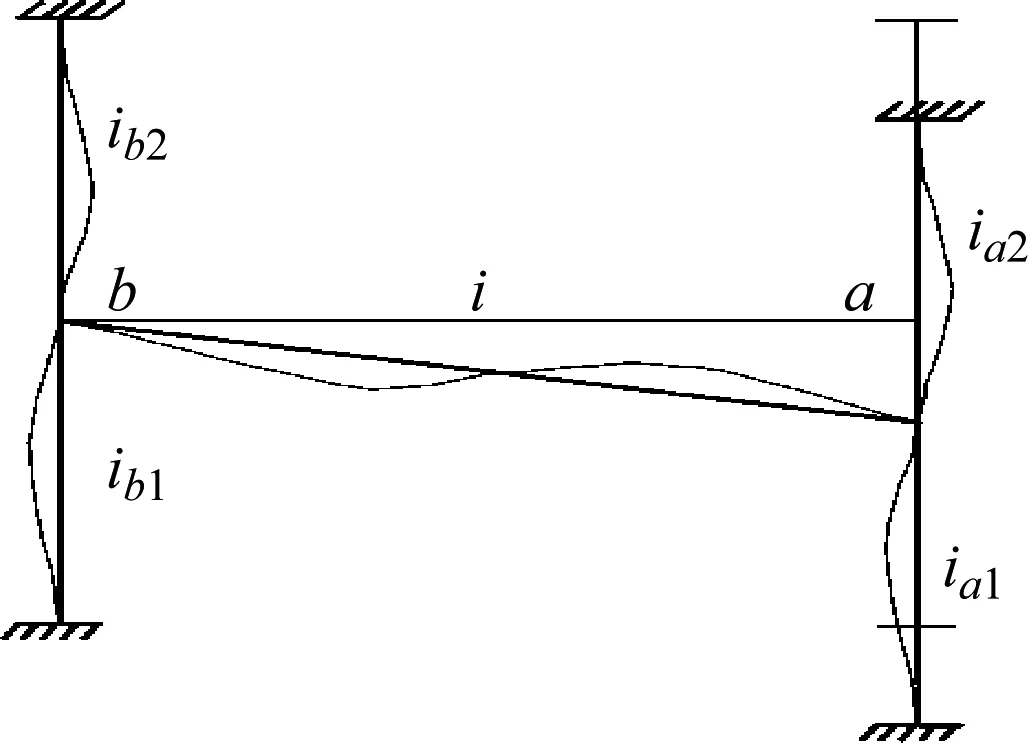
圖 6 框架結構豎向剛度計算示意

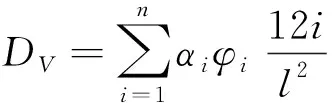
(1)

式中：

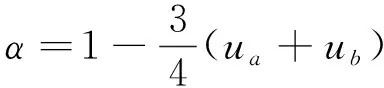
(2)

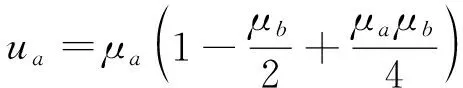
(3)

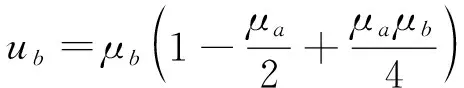
(4)

式中：為梁段的長度；為上部結構豎向剛度的貢獻衰減系數，具體取值可參考文獻[12]；為桿在節點的分配系數；為桿在節點的分配系數。

將=025、=019及框架梁的線剛度代入式(1)，得到框架結構豎向剛度為4881 kN/mm，即層均剛度為81.4 kN/mm。

2.2 托換結構剛度

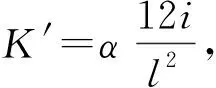
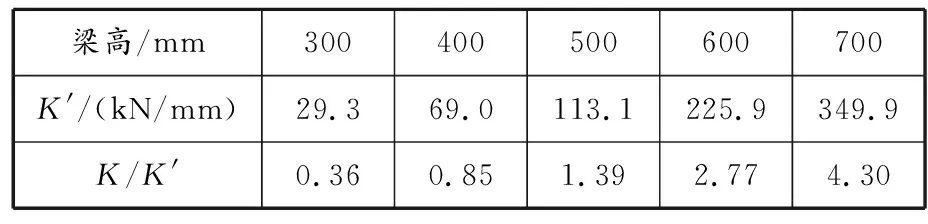
表 2 托換結構豎向剛度及其與框架結構層均剛度比值

3 有限元模型建立

基于算例的截面和配筋設計，應用Abaqus軟件分別建立上部框架結構和托換結構計算模型：首先僅對上部框架結構柱底施加位移，得到框架結構豎向剛度數值解；然后建立框架結構與托換結構整體模型，通過位移加載，對整體結構進行受力分析。

3.1 材料參數

混凝土材料本構選用Abaqus軟件提供的塑性損傷本構模型，采用文獻[13]提出的混凝土本構模型模擬混凝土的受力性能，混凝土本構關系方程為

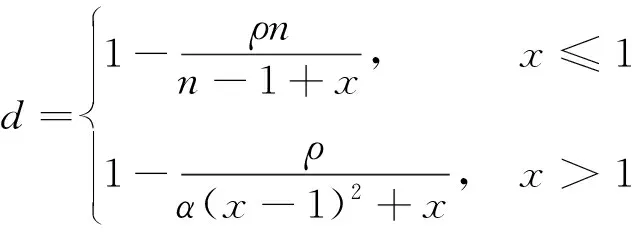
(5)

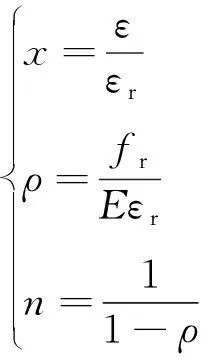
(6)

式中：為混凝土單軸受壓或受拉應力-應變曲線下降段參數值；為混凝土單軸抗壓或抗拉強度代表值；為與單軸抗壓或抗拉強度相應的混凝土峰值壓應變或拉應變；為混凝土單軸受壓損傷演化參數。

該混凝土本構模型對《混凝土結構設計規范》(GB 50010—2010)中混凝土本構關系式出現負損傷的情況進行優化，使其更符合混凝土實際受力狀態。損傷因子選用基于楊飛等單軸受力曲線的圖解法得到,鋼筋本構模型采用《混凝土結構設計規范》建議的雙折線彈塑性應力-應變模型。

3.2 單元選取

上部鋼筋混凝土框架和下部托換結構均采用8節點線性縮減積分六面體單元C3D8R，框架結構混凝土與托換結構混凝土結合面默認無相對滑移，采用Tie連接。為便于施加位移載荷，托換節點下部增設剛性墊塊，防止將載荷直接作用于混凝土，導致混凝土局部應力過大而壓碎，墊塊與托換結構間采用Tie連接。鋼筋采用線性三維桁架單元T3D2，嵌入混凝土單元。

3.3 約束條件

約束條件(1)：單獨對上部框架結構A軸各柱的柱底施加向上10 mm位移，另外2個方向位移為0，其余各柱各方向位移為0(見圖7)，獲取A軸柱底支反力之和與支座位移曲線。

圖 7 柱底位移約束

約束條件(2)：建筑物頂升糾傾工程由布置在每個托換節點下方的千斤頂提供頂升力，千斤頂布置在每個托換節點的四角。對每個托換節點底部的剛性墊塊施加不同的豎向位移，模擬建筑物頂升過程，托換節點位移約束示意見圖8。

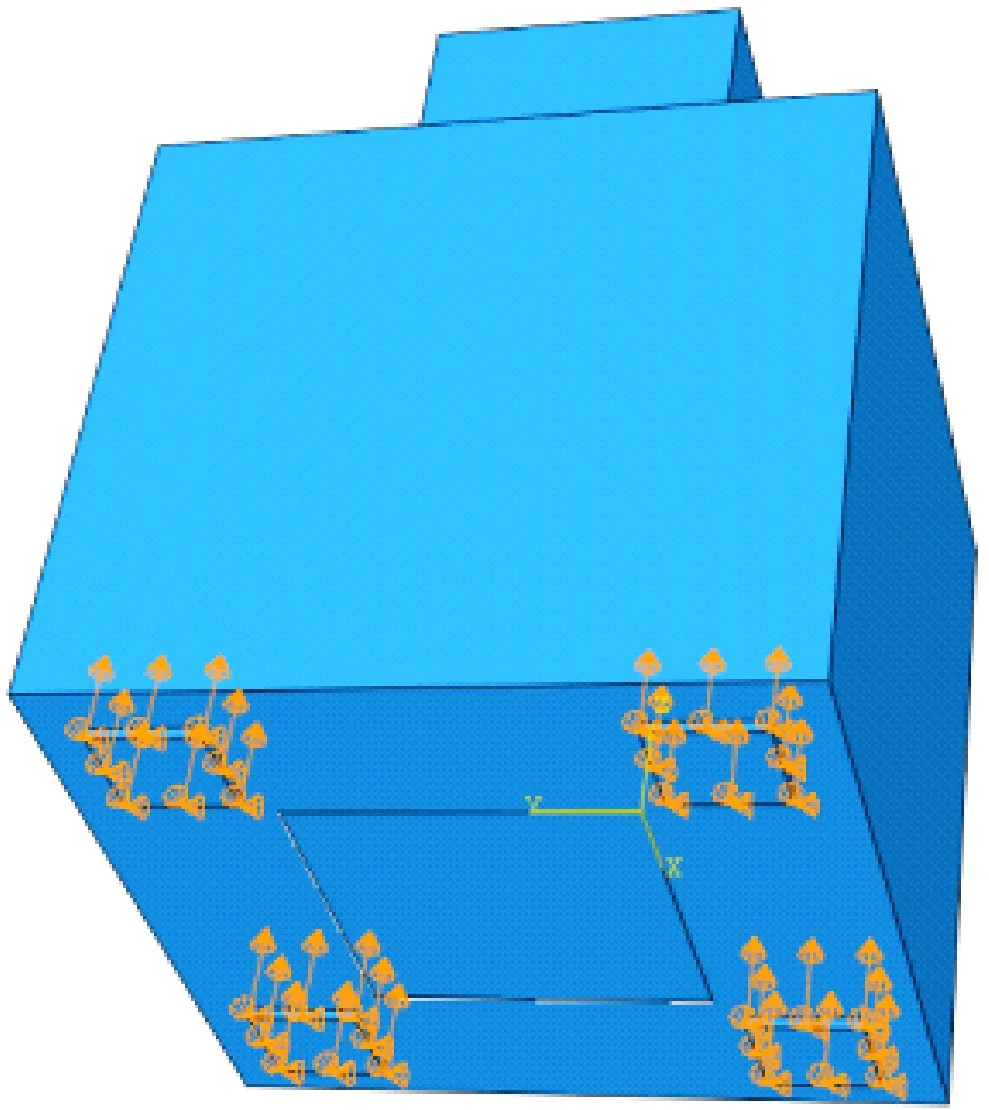
圖 8 托換節點位移約束示意

根據建筑物傾斜糾偏設計和驗收標準，建筑物高度小于等于24 m、傾斜量大于傾斜方向建筑物長度的4‰時需要進行糾傾加固，因此分別模擬不同連梁高度的整體結構分別在縱向頂升6‰和8‰的該方向長度(定義為糾傾率)時結構的受力情況，每排柱的托換節點頂升量見表3。

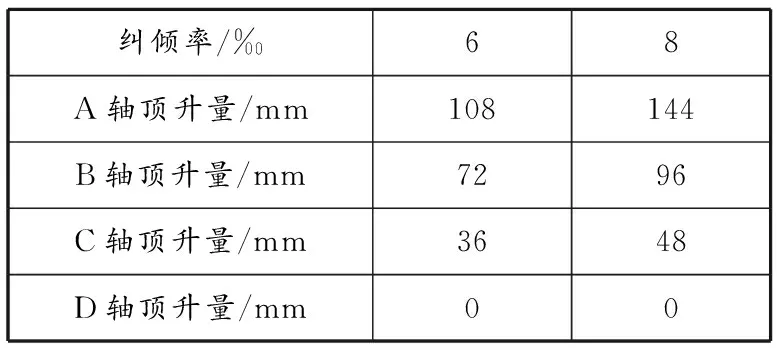
表 3 不同糾傾率時各軸托換節點頂升量

4 有限元模型分析

4.1 模擬求解結構豎向剛度

為驗證式(1)框架結構豎向剛度計算的準確性，通過數值模擬的方法，利用剛度定義求解框架結構豎向剛度，采用約束條件(1)得到的A軸柱底支反力之和與支座位移的關系見圖9。

圖 9 A軸柱底支反力之和與支座位移關系曲線

支座位移小于5 mm時曲線斜率基本不變，因此認為支座位移為0～5 mm時結構處于彈性階段；支座位移大于5 mm后結構處于彈塑性階段，故該段斜率即為框架結構豎向剛度。根據圖9，框架結構豎向剛度約為485.3 kN/mm，即層均剛度為80.9 kN/mm。該結果與解析解結果基本一致，可驗證解析結果的可靠性。

4.2 模擬建筑物糾傾受力分析

采用約束條件(2)進行框架糾傾結構頂升糾傾模擬，在縱向連梁高度為400 mm、糾傾率為6‰的情況下，整體結構的VON MISES應力云圖見圖10。應力較大部位主要集中在上部結構的第1層柱和托換結構，結構應力隨層數的增高逐漸減小。其他工況的應力分布也呈現同樣的規律。

圖 10 整體結構應力云圖,Pa

建筑物糾傾率為8‰時，第1層2軸各柱的VON MISES應力云圖見圖11。

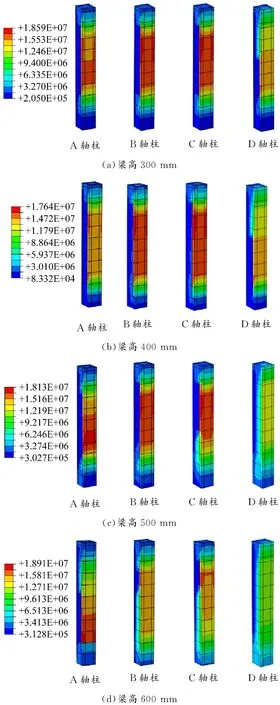
圖 11 糾傾率為8‰時第1層2軸各柱的應力云圖,Pa

隨著梁高的增大，框架柱的應力先減小后增大，梁高為400 mm時應力最小；應力逐漸向A軸柱集中，梁高為400 mm時各軸柱受力均勻，最為合理。糾傾率為6‰時，也呈現出同樣的規律。

綜合各工況的模擬結果，得到梁高與結構最大應力的關系見圖12。當梁高為300 mm時,結構的最大應力與無連梁情況差別不大，未明顯體現出連梁的作用。當梁高為400 mm時，上部結構的最大應力達到最小值。當梁高大于500 mm時，隨著梁高增大，結構的最大應力值也逐漸增大。

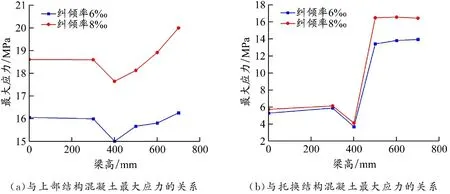
圖 12 梁高與結構最大應力關系曲線

4.3 托換結構設計推薦剛度值

當梁高為400 mm時，糾傾過程中結構的受力狀態最優，此時托換結構與上部結構層均剛度的比值為0.85，接近于1，因此認為可以根據上部結構層均剛度確定托換結構連梁的剛度和高度，使糾傾過程中上部結構受力更加合理。

5 結 論

以某6層框架結構為例，對上部框架結構和托換結構整體進行計算分析，主要結論如下。

(1)對比框架結構豎向剛度的數值計算結果與理論計算，二者吻合。

(2)在頂升糾傾工程中，結構頂升第1層柱受力最大;連梁高度小于300 mm時，連梁的作用不明顯。

(3)當托換結構的豎向剛度與上部結構的層均剛度相近時，托換結構受力最合理。