三峽庫區低山丘陵區多尺度景觀指數響應及適宜粒度

華 琳,黃志霖,*,馬 良,黃嘉元,周高峪

1 中國林業科學研究院森林生態環境與自然保護研究所，國家林業和草原局森林生態環境重點實驗室，北京 100091

2 秭歸縣林業局, 宜昌 443631

景觀格局是指大小和形狀不一的景觀斑塊在空間上的排列鑲嵌,具有典型的空間異質性和尺度依賴性[1—2]。明確景觀格局的尺度效應是揭示景觀格局及其變化的重要前提,合適的尺度是生態學研究中的起點和基礎,影響生態系統格局和過程規律分析的準確程度,最終影響到研究成果的科學性和實用性[3—5]。而進行生態系統和生態過程的大尺度生態問題研究時,需進行小尺度景觀數據信息的跨尺度傳遞,最大程度的保留原生態過程的景觀格局特征,因此探討中小尺度下的景觀格局特征以及在各尺度之間的信息傳遞變化規律則是研究景觀格局尺度效應的基礎。

景觀格局的尺度效應主要涉及空間粒度、空間幅度和同時考慮空間粒度和空間幅度三個方面。已有的研究案例多聚焦某一固定空間幅度中的空間粒度變化對景觀格局的影響。例如,市級行政區[6—|10]、區縣級行政區[11—13]、小流域[14—16]及三峽庫區[17—20]、青海湖流域[21]等特定區域[22]。在不同空間幅度對景觀格局的影響方面研究較少,主要以不同空間幅度大小的移動窗口[23—25]和從研究區域中心向外擴展[26—29]進行景觀格局分析。空間尺度的幅度和粒度不是割裂的,當前研究多只針對空間幅度和空間粒度的單一方面進行分析,少有同時兼顧空間幅度和粒度的景觀格局分析[30],且同一水平尺度域內的景觀格局特征推演比較容易,垂直跨越多個尺度域的景觀格局分析較復雜[4]。因此,亟待明確景觀在不同空間幅度研究區的粒度響應特征。

用景觀指數描述景觀格局及其變化,是景觀生態學最常用的定量化研究方法。目前大多通過景觀指數在不同粒度下的變化趨勢分析景觀整體格局和各景觀類型的響應,現有研究顯示景觀指數對尺度變化的響應具有一定的線性或非線性特征。近年來,景觀指數響應曲線進行擬合函數分析的研究開始受到關注,主要包括冪函數、二次多項式函數、對數函數、線性函數、分段階梯函數等函數擬合[21,31—37],但目前仍以響應曲線的粗略轉折點位置為依據,較少根據擬合函數的特征進行適宜粒度閾值的分析,而利用擬合函數的頂點、最大曲率點等特殊點進行閾值推算精確且具有普適性。

秭歸縣是三峽庫區重要的低山丘陵地貌區,是三峽庫區的壩上第一縣,是我國退耕還林示范縣和國家林草局退耕還林科技支撐示范點,正開展建設“山水林田湖草”生命共同體綜合治理示范模式。三峽庫區是《全國重要生態系統保護和修復重大工程總體規劃(2021—2035年)》中的水土保持國家重點生態功能區。隨著生態環境治理的進行,三峽庫區的植被覆蓋率逐年提升、生態環境有所改善,但仍然存在林草植被質量整體不高,水土流失、生物多樣性受損嚴重等問題,總體水平仍較為脆弱,生態承載力和環境容量仍有不足,經濟發展帶來的生態保護壓力依然較大。多尺度景觀格局的變化特征和分析粒度閾值在三峽庫區這一地形復雜和人地關系較為緊張的區域需進一步明確。本文以湖北省秭歸縣為研究區域,基于高分辨率影像的解譯數據,選取主要的景觀格局指數,在縣域、鄉鎮和小流域尺度上進行景觀格局的粒度效應分析,并進行擬合函數分析以探討多尺度上景觀格局的粒度響應特征,分析垂直尺度上不同尺度之間景觀格局特征的變化以及推演各空間幅度上的適宜粒度閾值,為后續景觀格局、生態系統功能分析與森林景觀恢復和生態修復等提供研究基礎和空間粒度大小選擇的參考。

1 研究區概況

秭歸縣(110°59′34″E—110°20′26″E,30°38′22″N—31°11′28″N)位于三峽庫區庫首(圖1),面積為2427km2。秭歸縣下轄8鎮4鄉,鄉鎮的平均面積為189km2,分布有251個小流域,平均面積為9.03 km2。總體地勢南高北低,最高點在西南部,地形地貌主要以山地丘陵為主。

圖1 研究區地理位置Fig.1 Geographical location of the study area

2 數據來源與研究方法

2.1 數據來源

本文所采用的數據主要包括秭歸縣土地利用矢量數據、空間分辨率為10m的高程數據、行政區劃數據和小流域邊界數據。土地利用數據以秭歸縣2018年0.2m空間分辨率的航空攝影影像數據為基礎,結合實地調查進行目視解譯獲得。根據《土地利用現狀分類標準GB/T21010—2017》并結合實際地域特征,將秭歸縣的土地利用數據分為九類,包括耕地、園地、林地、草地、工礦用地、住宅用地、交通運輸用地、水域、其它用地。小流域的邊界數據由數字高程模型(Digital Elevation Model,DEM)數據以流量10000cell為閾值進行水文分析得到,共251個小流域。

2.2 空間尺度的選擇

空間幅度方面選取垂直等級上面積大小不同的縣域、鄉鎮、小流域三個幅度,面積逐步擴大,分別呈21、13倍的遞增關系。空間粒度方面,將土地利用現狀圖矢量數據轉化為柵格數據,柵格像元的大小即為空間粒度的大小。矢量數據轉換柵格數據主要有三種屬性分配原則,如圖2所示：(1)中心要素分配屬性值原則,位于柵格單元中心位置的面要素a決定像元的屬性。(2)最大面積要素分配屬性值原則,柵格單元內最大面積的單個要素b決定像元的屬性。(3)最大合并面積要素分配屬性值原則,柵格單元內多個相同屬性的要素合并后,具有最大面積的要素c決定像元的值。借鑒前人的研究和數據計算的數量將土地利用矢量數據分別按照三種屬性分配原則轉換成粒度大小為1、2、3、4、5、7、9、1 0、12、15、20、25、30、40、50、90、100、120、150、180、200、300、400m的柵格數據以進行最佳屬性分配原則的選擇和景觀指數分析。

圖2 中心、最大面積、最大合并面積屬性分配原則 Fig.2 The principle of distribution of attributes of center, maximum area, and maximum combined area a、b、c、d:對應要素的屬性

2.3 景觀指數的選擇

景觀指數的選擇對景觀格局的分析至關重要,景觀指數包括斑塊、類型和景觀3種水平。本文以景觀水平分析為主,在綜合國內外研究和避免冗余分析的基礎上[38—41],選取如下指數：組成特征方面選取斑塊密度(Patch Density, PD)、邊緣密度(Edge Density, ED)、最大斑塊面積指數(Largest Patch Index, LPI)、平均斑塊大小(Mean Patch Size, AREA_MN),形狀特征方面選取景觀形狀指數(Landscape Shape Index, LSI)、平均形狀指數(Mean Patch Shape Index, SHAPE_MN)、周長面積分維數(Perimeter-Area Fractal Dimension, PAFRAC)、平均分維數(Mean Patch Fractal Dimension, FRAC_MN),聚散性方面選取蔓延度指數(Contagion Index, CONTAG)、相似鄰接比例指數(Percentage of Like Adjacency, PLADJ)、散布與并列指數(Interspersion and Juxtaposition Index, IJI)、分離度指數(Splitting Index, SPLIT)、景觀分割度指數(Landscape Division Index, DIVISION)、凝聚度指數(Patch Cohesion Index, COHESION)、斑塊連接度指數(Connectance Index, CONNECT)、聚合度(Aggregation Index, AI),多樣性特征方面選取香農多樣性指數(Shannon′s Diversity Index, SHDI)和辛普森多樣性指數(Simpson′s Diversity Index, SIDI)。

2.4 研究方法

在ArcGIS10.4軟件中,按照最大面積要素分配原則、最大合并面積要素分配原則、中間要素分配原則三種屬性分配原則,將秭歸縣土地利用類型的矢量數據以1、2、3、4、5、7、9、10、12、15、20、25、30、40、50、90、100、120、150、180、200、300、400m為空間粒度進行柵格化,根據實際面積與各屬性分配原則生成的面積相比,分析三種屬性分配原則的優劣,從中挑選最適合的屬性分配原則,繼而進行12個鄉鎮和251個小流域矢量數據不同空間粒度的柵格化,共計6072幅柵格數據。通過Fragstats4.2軟件進行景觀指數計算,分別統計12個鄉鎮和251個小流域的景觀指數平均值代表鄉鎮幅度和小流域幅度的景觀指數,并以空間粒度大小為x軸,景觀指數數值為Y軸繪制折線圖,分析景觀格局指數的粒度響應變化。選擇線性函數、指數函數和冪函數等擬合景觀指數對粒度變化的響應曲線,選擇擬合度最高的函數,根據其擬合函數的特性(最大曲率點、極值點)選取景觀分析的適宜粒度范圍。其中最大曲率點公式如下[42]：

式中,y″(x)為二階導數,y′(x)為一階導數。

3 結果與分析

3.1 不同屬性分配原則對景觀指數的影響

不同屬性分配原則產生了景觀面積與實際面積的差異,影響景觀指數的粒度響應變化。圖3中左圖為不同分配原則下各粒度的景觀總面積,最大面積要素分配原則和最大合并面積要素分配原則下不同粒度的景觀面積變化相似,兩者之間差異較小。中間要素分配原則的景觀面積變化程度較小,在粒度增加的過程中有所波動,總體上升。圖3中右圖為各粒度下景觀面積與真實面積之差,三種屬性分配原則下的景觀面積與實際面積的差異較為明顯,中心要素分配原則與實際面積差異最小更適合用于景觀分析。

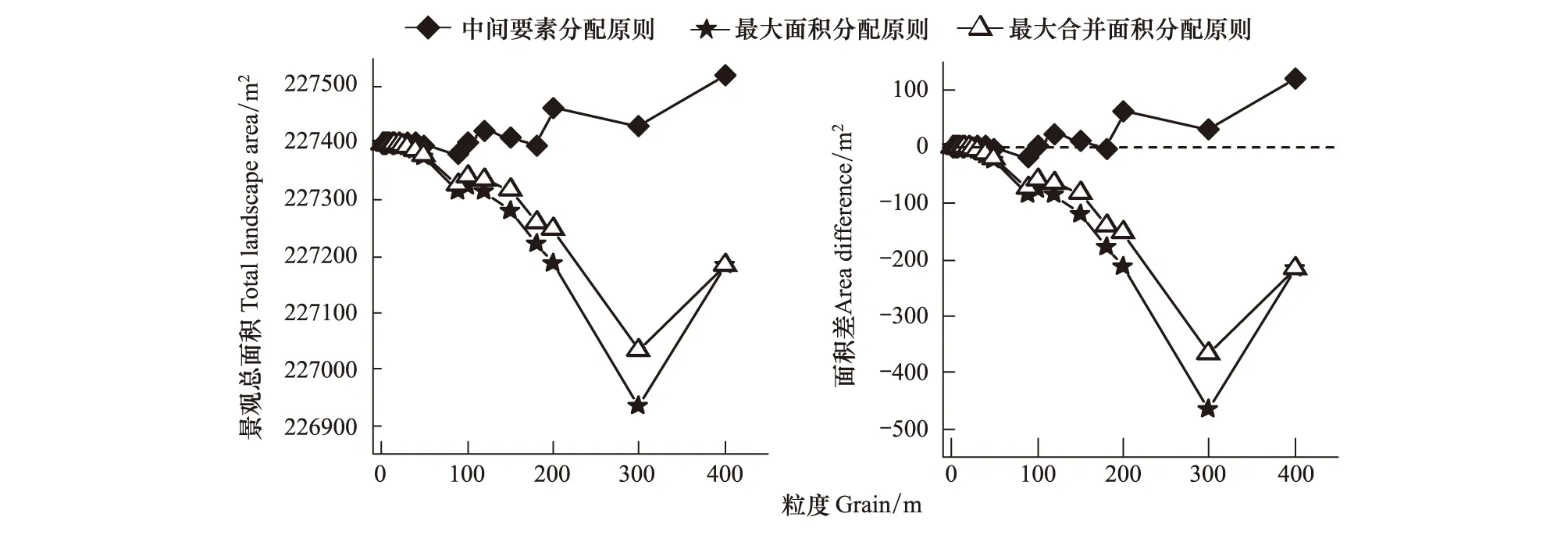
圖3 三種分配原則下不同粒度景觀總面積與真實景觀面積差異Fig.3 The difference between the total landscape area and the real landscape area of different granularities under the three allocation principles

3.2 景觀指數的粒度響應

3.2.1縣域幅度景觀指數的粒度響應

縣域斑塊密度指數的第一處變化發生在5m處,5—50m呈現急劇降低的狀態；邊緣密度、景觀形狀指數、周長面積分維數、蔓延度、相似鄰接比例、散布與并列指數和聚合度指數均在1—100m粒度范圍內變化顯著；最大斑塊面積指數在1—30m粒度范圍內增加顯著；平均斑塊大小指數在小于50m的范圍內變化和緩,50—400m粒度范圍內增加顯著；平均形狀指數和平均分維數指數在小于50m的粒度范圍內急劇降低；分離度指數和景觀分割度指數分別在1—7m和1—30m的粒度范圍內急劇降低,繼而波動下降；凝聚度指數整體呈現直線式下降趨勢；斑塊連接度指數在1—10m粒度范圍內下降后在10—300m粒度范圍內呈現增加的趨勢；多樣性指數均在1—100m粒度范圍內變化穩定,100—400m粒度范圍內上下波動大(圖4)。

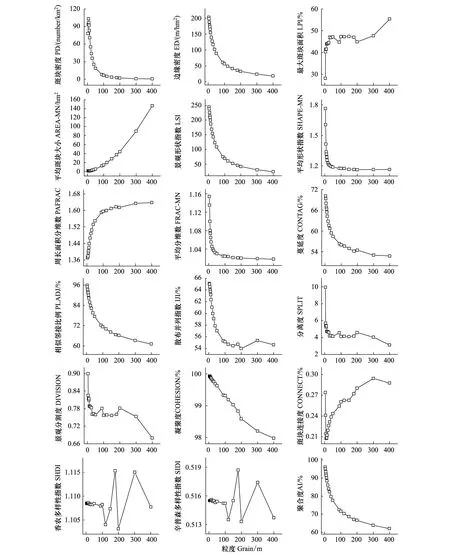
圖4 縣域的景觀指數曲線Fig.4 The landscape index curve of the county

3.2.2鄉鎮幅度景觀指數的粒度響應

在鄉鎮幅度層次,斑塊密度指數的增加狀態同樣也在5m處發生轉折；邊緣密度指數、相似鄰接比例、聚合度指數均在1—100m粒度范圍內變化顯著；最大斑塊面積指數在1—20m粒度范圍內增加顯著；平均斑塊大小指數在1—50m范圍內變化和緩；景觀形狀指數、周長面積分維數、蔓延度在2m和100m處有所轉折,且在100m范圍內變化顯著；平均形狀指數在30m粒度處有轉折；平均分維數指數在3m和50m粒度處有轉折；散布與并列指數在1—100m粒度范圍內下降之后又呈現增加狀態,但在1—5m粒度范圍內較穩定；分離度指數和景觀分割度指數均分別在1—5m和1—20m粒度范圍內下降顯著后變化和緩；凝聚度指數整體呈現直線式下降趨勢；斑塊連接度指數在1—10m迅速下降,在10—120m粒度范圍內呈現增加的趨勢,120—400m粒度范圍波動增大；多樣性指數均在1—2m內下降顯著,2—200m粒度范圍內較穩定,200—400m范圍內波動增加(圖5)。

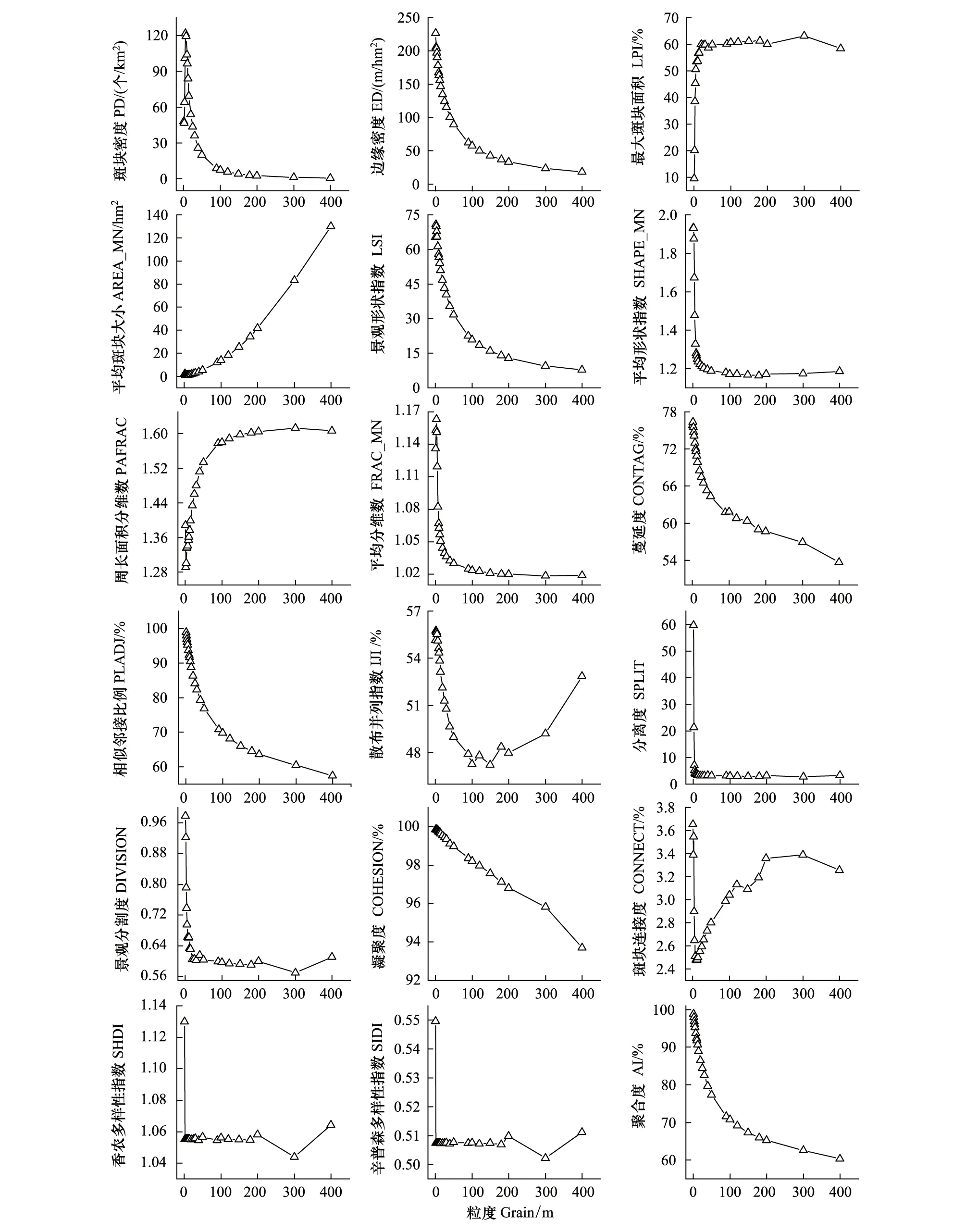
圖5 鄉鎮的景觀指數曲線Fig.5 The landscape index curve of the township

3.2.3小流域幅度景觀指數的粒度響應

小流域幅度上的景觀格局指數變化與鄉鎮幅度的變化趨勢相似,部分區域存在差異。斑塊密度指數先在1—5m粒度范圍內增加后到100m范圍內顯著降低；邊緣密度指數、景觀形狀指數、蔓延度、相似鄰接比例指數、聚合度指數在1—100m粒度范圍內降低變化顯著；最大斑塊面積指數在1—20m粒度范圍內增加顯著,20—400m粒度范圍內變化和緩；平均斑塊大小指數在1—50m范圍內變化和緩；平均形狀指數在25m粒度處發生轉折；周長面積分維數在3m和100m粒度處轉折顯著；平均分維數指數在3m和50m粒度處有轉折；散布與并列指數在50m粒度范圍內下降后不斷增加；分離度指數在1—4m粒度范圍內下降迅速后變化和緩；景觀分割度指數在1—20m粒度范圍內下降顯著；凝聚度指數整體呈現直線式下降趨勢；斑塊連接度指數在1—3m內增加,3—15m粒度范圍內呈現下降的趨勢,15—120m內波動增大,200—400m范圍內不斷降低；多樣性指數中,1—50m粒度范圍內穩定,50—400m粒度范圍內波動增加(圖6)。

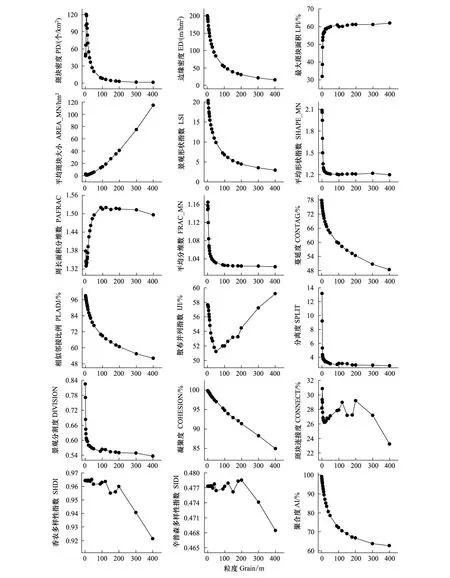
圖6 小流域的景觀指數曲線Fig.6 Landscape Index Curve of Small Watershed

3.3 各尺度景觀指數的擬合函數

斑塊密度、邊緣密度、景觀形狀指數等景觀指數隨粒度變化響應的曲線可以高度擬合函數,且不同空間幅度上的擬合函數參數有所不同(表1、表2、表3)。部分景觀指數的響應曲線可以擬合多個函數,從中選取R2最大的函數進行分析。擬合函數主要為三種：冪函數及其組合、指數函數及其組合和線性函數。對擬合函數求取極值點和最大曲率點,得出小流域、鄉鎮、縣域三個幅度斑塊密度的極值點分別位于為5.65m、5.73m、5.78m處,最大曲率點均為34m；邊緣密度的最大曲率點分別為48m,46m,46m；最大斑塊指數的最大曲率點分別為7m、9m、9m；平均斑塊面積、平均形狀指數、平均分維數、蔓延度指數的最大曲率點均為3m；景觀形狀指數的最大曲率點分別為3m、10m和53m；三個幅度的周長面積分維數最大曲率點均為400m；分離度指數的最大曲率點分別為5m、5m、7m；景觀分割度指數的最大曲率點分別為4m、4m、7m；相似鄰接比例指數和聚合度的最大曲率點均位于10m處；散布與并列指數的最大曲率點分別為400m、35m、25m。

表1 縣域景觀指數的擬合函數Table 1 Fitting function of landscape index of the County

表2 鄉鎮景觀指數的擬合函數Table 2 Fitting function of landscape index of township

表3 小流域景觀指數的擬合函數Table 3 Fitting function of small watershed landscape index

3.4 不同幅度下景觀格局粒度響應的差異特征

縣域,鄉鎮和小流域三個幅度隨著粒度的增加,各景觀指數呈現出不同的變化趨勢,主要為三種變化趨勢：總體上升、總體下降和波動變化。邊緣密度、景觀形狀指數、平均形狀指數、平均分維數、蔓延度、相似鄰接比例、分離度、景觀分割度、凝聚度、聚合度均呈現總體下降的趨勢,最大斑塊面積指數、平均斑塊大小指數、周長面積分維數則呈現總體上升的趨勢。斑塊密度、散布與并列指數、斑塊連接度指數、多樣性指數均呈現波動變化(圖7)。

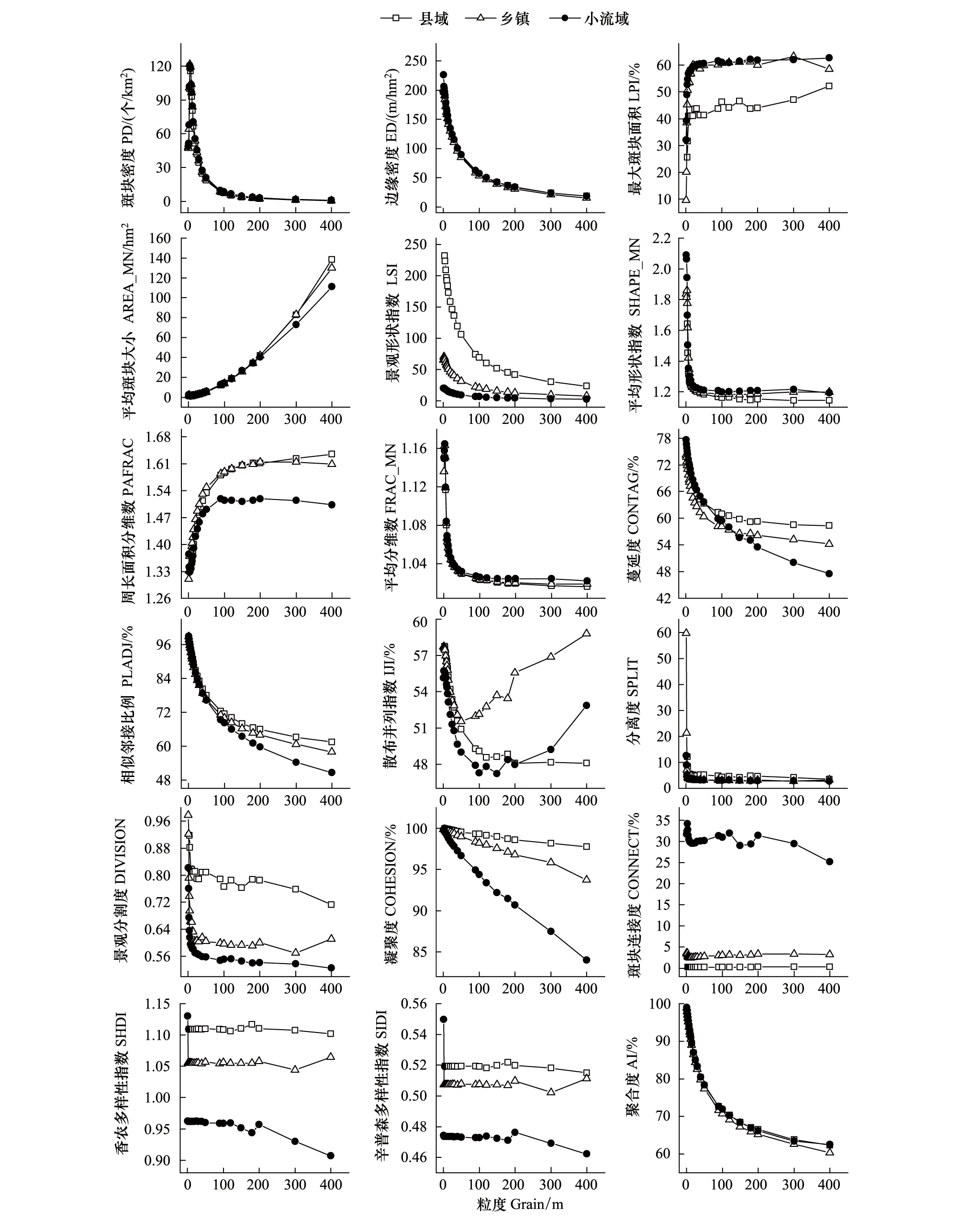
圖7 三個幅度的景觀指數曲線對比Fig.7 Comparison of landscape index curves of three ranges

三個幅度水平上斑塊密度、邊緣密度、聚合度指數的景觀指數數值與變化相近,區別不明顯；最大斑塊指數中,鄉鎮和小流域數值相近且大于縣域；平均斑塊大小指數中,1—200m范圍內三個幅度的數值相近,200—400m范圍內差異增加且呈現縣域>鄉鎮>小流域的狀態；平均形狀指數、平均分維數中1—50m范圍內數值相近,50—400m范圍內的差異有所增加,呈現小流域>鄉鎮>縣域的狀態。景觀形狀指數、景觀分割度、凝聚度指數和多樣性指數數值總體上縣域>鄉鎮>小流域；周長面積分維數中,鄉鎮和縣域的數值相近且大于小流域的數值；在蔓延度指數中,50m—150m范圍內三個幅度水平的數值交叉,1—50m內小流域>縣域>鄉鎮,150—400m內縣域>鄉鎮>小流域；相似鄰接比例指數中,1—50m范圍內三個幅度的指數數值相近,50—400m范圍內的差異增加且呈現縣域>鄉鎮>小流域的狀態。散布與并列指數中,1—50m范圍內小流域和縣域的數值相近且大于鄉鎮,50m—400m范圍內小流域數值最大,鄉鎮數值增加且超過縣域；分離度指數中,總體上縣域>鄉鎮和小流域,小流域和鄉鎮數值相近；連接度指數中小流域>鄉鎮>縣域。

綜合三個幅度的景觀指數轉折變化點和擬合函數的最大曲率點、極值點,縣域、鄉鎮、小流域三個幅度的景觀指數適宜粒度見表4。部分指數如斑塊密度、邊緣密度、平均斑塊大小、周長面積分維數、平均分維數、蔓延度、相似鄰接比例、聚合度、凝聚度指數對空間幅度的變化并不敏感,不適合進行適宜粒度閾值的推定。綜合最大斑塊面積指數、景觀形狀指數、平均形狀指數、散布與并列指數、分離度、景觀分割度、斑塊連接度指數的最大曲率點和轉折點,去掉不敏感的粒度值,選取剩余粒度數值中最小和最大的粒度作為第一尺度閾值和第二尺度閾值,得出小流域、鄉鎮、縣域的第一尺度閾值分別為3m、4m、7m,第二尺度閾值分別為50m,100m,100m。

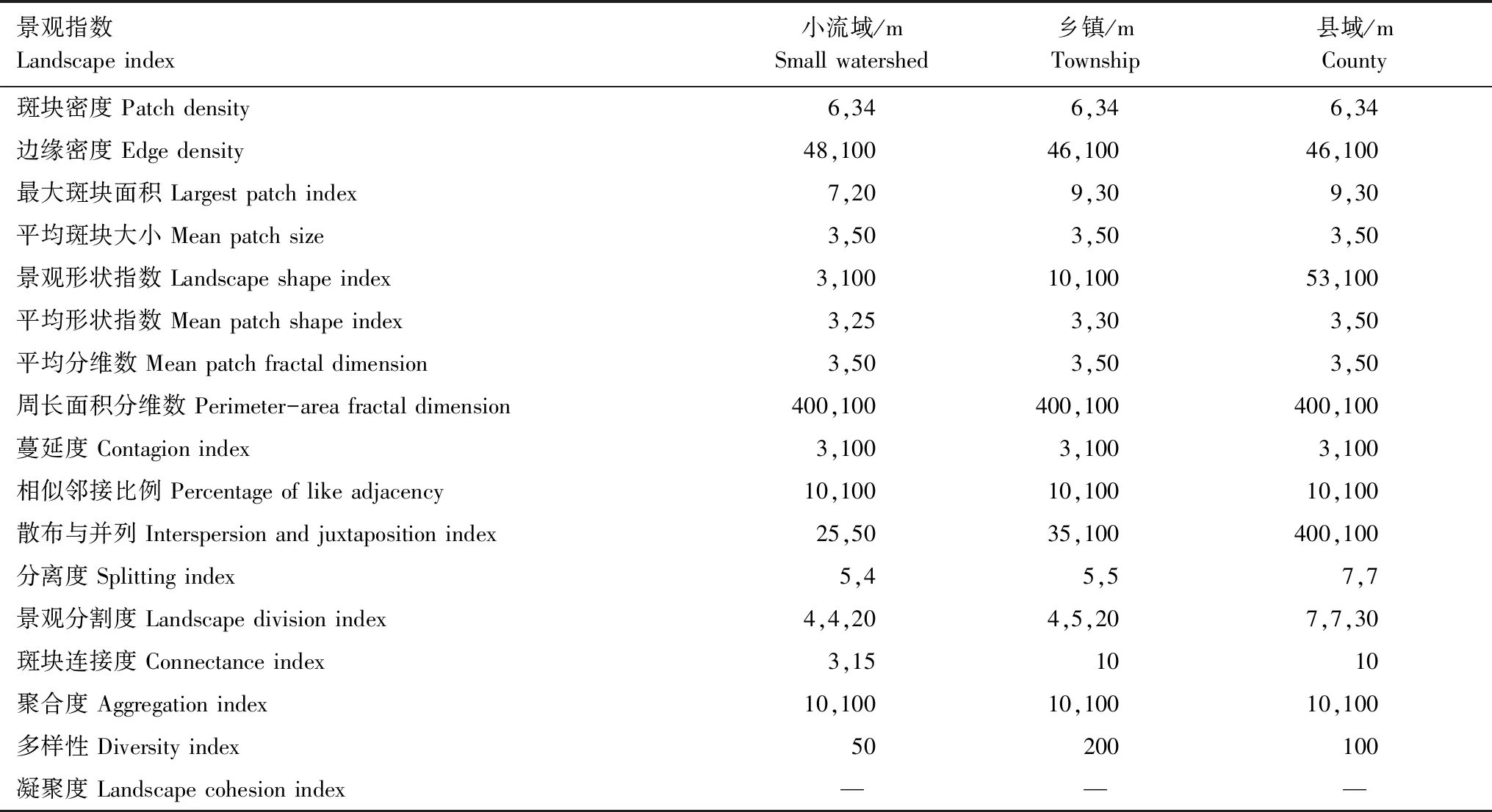
表4 縣域、鄉鎮、小流域的景觀指數最大曲率點、轉折點Table 4 Maximum curvature point and turning point of landscape index in county, township and small watershed

4 結論與討論

4.1 結論

空間數據屬性分配聚合原則的差異影響景觀指數的結果,其中心分配屬性原則下的面積差異較小,更為適合景觀格局分析。通過分析擬合函數的特征,利用極值點、最大曲率點特征能夠解決人工判斷指數轉折點的不統一問題,更合理的找出景觀分析的適宜粒度,如斑塊密度的擬合函數極值點位于5.8m處,精度高于目測的7m。

不同景觀指數對空間粒度變化的響應不同,大部分有明顯轉折變化,而凝聚度指數隨著粒度變化呈現直線式變化。部分景觀指數如斑塊密度、最大斑塊面積等對斑塊形狀和大小的變化非常敏感,部分指數如多樣性指數則敏感度較低。不同景觀指數對空間幅度大小變化的響應也不同,景觀形狀指數、凝聚度、多樣性指數和連接度指數的幅度變化敏感性高,前三者的空間幅度越小,景觀指數越小,而連通度空間幅度越小,景觀指數越大；斑塊密度、邊緣密度、聚合度的空間幅度敏感性低,無明顯變化；其他指數空間幅度的變化與空間粒度關系密切,空間粒度越大,變化越明顯。

斑塊密度、邊緣密度、平均斑塊大小、周長面積分維數、蔓延度、相似鄰接比例等指數對空間幅度的變化并不敏感,不適合進行粒度閾值的推定；最大斑塊面積、景觀形狀指數、平均形狀指數、散布與并列指數、分離度、景觀分割度、聚合度指數對空間幅度的變化敏感,適合推定不同幅度上的適宜粒度。小流域、鄉鎮、縣域的第一尺度閾值分別為3m、4m、7m,第二尺度閾值分別為50m,100m,100m,幅度越小的研究區景觀分析的適宜粒度越小,所需要的空間信息越詳細。隨著粒度的增加,空間信息和景觀信息喪失度增加,在一定的粒度達到穩定,所以在不影響計算的基礎上粒度的選擇越小越好。

4.2 討論

目前在三峽庫區的景觀格局粒度響應研究較少,且已有的研究僅從庫區整個幅度上進行分析[17-18],本文對三峽庫區低山丘陵區垂直等級上縣域、鄉鎮、小流域不同幅度進行了粒度響應分析,較前人的研究分析更為全面和深入。研究結果適合在今后的三峽庫區生態修復、森林景觀恢復等工程中進行應用,并在應用中驗證和推廣。

多數研究者基于30m及以上分辨率的數據進行分析,而30m分辨率的數據已經壓縮了景觀格局信息,致使景觀適宜粒度的遠遠大于30m,而無人機航測等高分辨率數據源產生的矢量數據更好的保留了原有景觀格局信息,所得適宜粒度結果小于前者,這與李佳佳[43]、汪桂芳[44]等人的研究結果相符。

在數據處理過程中,不同屬性分配原則下矢柵轉換導致的誤差容易被忽略,多數研究未考慮該誤差[18,35,43],影響結果的可靠性,本文研究發現中心要素分配屬性原則的景觀面積與實際面積誤差相較于其他原則小,最適宜景觀格局的分析。此外通過柵格數據直接進行聚合也有不同的規則,適宜原則也需進行下一步探討。由于柵格化,各斑塊的邊界由連續變化的曲線變得平直,部分反應斑塊形狀特征的指數,如景觀形狀指數,邊緣密度等,對邊界的變化更加敏感,需要區別與其他景觀指數進行分析。目前關于柵格化對景觀指數影響的定量分析較少,接下來可進行深入探討,對比柵格和矢量數據的景觀指數變化。最大斑塊面積、景觀形狀指數、平均形狀指數、散布與并列指數、分離度、景觀分割度、聚合度指數對空間幅度的變化敏感度高,與前人的研究分析基本一致,代表性強且函數擬合效果較好,適合推定不同幅度上的適宜粒度,今后的研究中可通過這些指數進行粒度推定,減少數據處理量。已有的研究分析大多通過目視判斷指數曲線的趨勢變化以確定轉折點進而確定適宜粒度,適宜粒度的推定缺乏統一標準和精準度,而通過景觀指數曲線擬合函數的極值點、最大曲率點推斷適宜粒度更為精準,具有一定的普適性。

不同土地利用類型結構和景觀基質、斑塊、廊道的空間格局分布密切關系景觀格局,也影響景觀指數的變化和適宜粒度閾值的選擇,如道路對景觀格局的分割、生物廊道連接景觀斑塊,前人對不同土地利用類型的景觀指數變化研究較多,基質、廊道的景觀結構還需進行深入研究,且不同的分析方向需重點選擇相對應的類型和結構進行探討以選擇適宜的粒度。