SCR脫硝裝置大顆粒灰攔截網壓降特性

孟 磊，雷 彧，陳 晟，劉小偉，岳樸杰，谷小兵

(1.大唐環境產業集團股份有限公司，北京 100097；2.華中科技大學 煤燃燒國家重點實驗室，湖北 武漢 430074)

0 引 言

選擇性催化還原(Selective Catalytic Reduction,SCR)技術是我國當前燃煤鍋爐最主要脫硝手段[1-3]。我國燃煤鍋爐的SCR脫硝裝置幾乎全為無煙氣旁路的高塵布置[4]，煙氣中顆粒會導致催化劑磨損和堵塞。堵塞嚴重不僅會大幅降低裝置脫硝性能，甚至會導致主機非計劃停機[5]。其中，煙氣中尺寸大于催化劑通道的大顆粒灰是引起堵塞的重要原因[6-9]。目前國內外針對SCR裝置前的大顆粒灰防治技術可大致分為2類：① 對省煤器灰斗進行改造，通過增設擋板、導流板、擴容等方式調整流場結構[10-12]，利用慣性將大顆粒灰從煙氣中分離出來[13]；② 加裝大顆粒灰攔截網，在合適位置安裝帶孔攔截網，保證煙氣通過的情況下分離出大顆粒灰[14-16]。相比于前者，加裝攔截網技術具有對流場設計要求低、捕集效率高、改造與安裝方便等優點。目前，大顆粒灰攔截裝置已在國內百萬機組選擇性催化還原脫硝系統上成功應用[17]。然而，目前攔截網的設計依賴于試驗測量與工程經驗，缺少通用設計準則與理論依據，對于攔截網開孔形狀、煙氣流速、開孔率以及攔截網厚度等參數對攔截效率以及壓降的影響認識尚不深入。

針對上述問題，金理鵬等[18]研究了攔截網開孔形狀、外形結構與安裝位置對攔灰效率和系統阻力的影響，發現攔截網壓降與開孔率的3次方成反比，同時對比了屋脊式和平板式攔截網，發現二者阻力、攔灰效果基本相同。陳鴻偉等[19]通過冷態試驗發現長條形孔型的攔截網性能優于正方形開孔的攔截網，攔截網引起的壓降為140～160 Pa,大顆粒灰攔截效率可達92.2%，發現攔截網安裝角度與長度均會影響壓降。上述試驗進一步驗證了大顆粒灰攔截技術的可行性，但實際工程中對于攔截網壓降的要求較高，可接受的壓降范圍通常在150 Pa以內，在保證攔截效果的前提下應使壓降盡可能小。目前，試驗中攔截網引起的壓降仍較大，存在優化空間。此外，試驗手段難以對攔截網孔型、安裝位置、角度以及長度等參數同時全面測量從而找到最優參數。相比之下，計算流體力學方法(Computational Fluid Dynamics,CFD)能夠便捷地改變設計參數進行掃描計算，從而獲得攔截網最優設計方案。

由于攔截網網孔尺遠小于煙道尺寸，CFD計算建模長度尺度跨度大，因此常采用多孔介質對攔截網進行等效模擬，基于攔截網孔隙率和滲透率等宏觀參數即可等效求解出流場經過攔截網的壓力損失。已有研究采用CFD方法模擬了攔截網安裝在省煤器灰斗上方時的流場分布[16]，對攔截網單元和SCR系統整體流場分別進行了模擬，獲得流場分布、壓降信息[17]以及大顆粒灰運動軌跡[20]。其中滲透率表示多孔介質允許流體通過空隙流動能力的強弱，其大小與孔隙率、流體滲透方向上空隙的幾何形狀、顆粒大小以及排列方向等因素有關。等效多孔介質滲透率的準確估計對提升整體設備流場解的精確度具有重要意義，但并未對滲透率設置依據進行詳細探討。筆者通過CFD方法，利用Ansys Fluent仿真軟件對網孔尺度流場進行求解，探究攔截網開孔形狀、煙氣流速、開孔率以及攔截網厚度等參數對攔截網壓降的影響，進一步推導了達西定律下等效多孔介質滲透率的關聯公式，對于SCR系統整體CFD模擬以及攔截網選型設計具有重要意義。

1 研究方法

1.1 CFD計算模型

研究選取了3種最常見開孔形狀的攔截網作為研究對象：長條形、正六邊形和正方形攔截網。由于SCR催化劑通道的孔徑尺寸限制，粒徑大于4 mm的大顆粒灰即可造成催化劑床層堵塞[14]。為衡量攔截網對不同粒徑大顆粒灰的攔截效果，將攔截網可攔截的最小顆粒尺寸定義為“臨界尺寸”。不同開孔形狀攔截網的臨界尺寸如圖1(a)所示，其中a為臨界尺寸，x為相鄰網孔間的距離，λ為長條形網孔的長寬比，六邊形、正方形的臨界尺寸為其開孔的內接圓直徑，長條形的臨界尺寸為其開孔寬度，當3者的臨界尺寸一致，即可認為3者攔截效果一致。利用Ansys Fluent仿真軟件按照1∶1比例建立了攔截網局部網孔的三維模型，以長條形攔截網為例(圖1(b))，計算區域為網孔單位附近一個長方體區域，左側為煙氣入口，右側為壓力出口，具體參數見表1，其余邊界均設置為周期性邊界條件。模擬采用有限元分析法進行計算，在網格劃分時對攔截網單元附近等小尺度空間結構進行了網格加密處理，網格總數約200萬個。

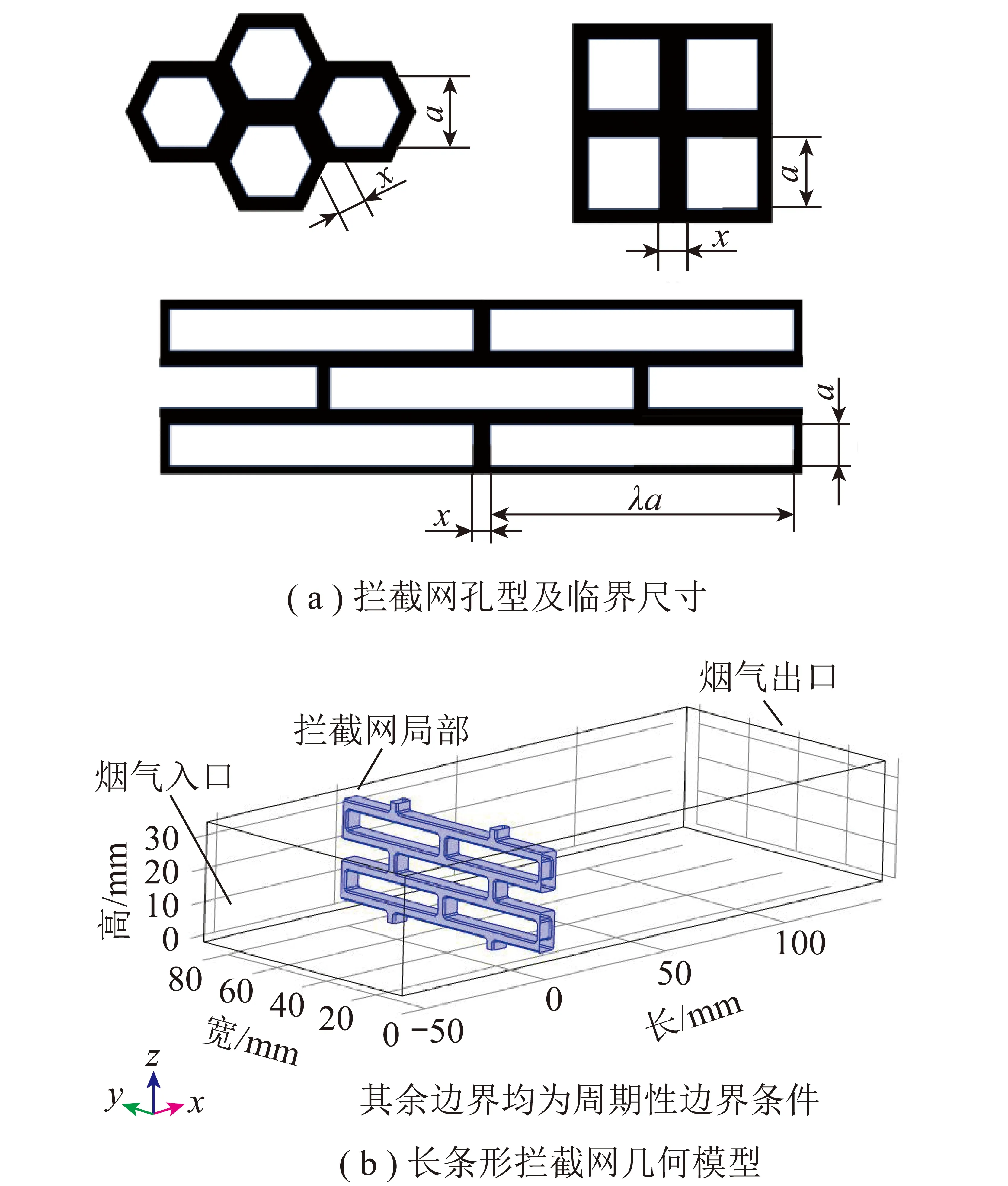
圖1 攔截網局部CFD計算模型Fig.1 Pore-scale CFD model of interceptor

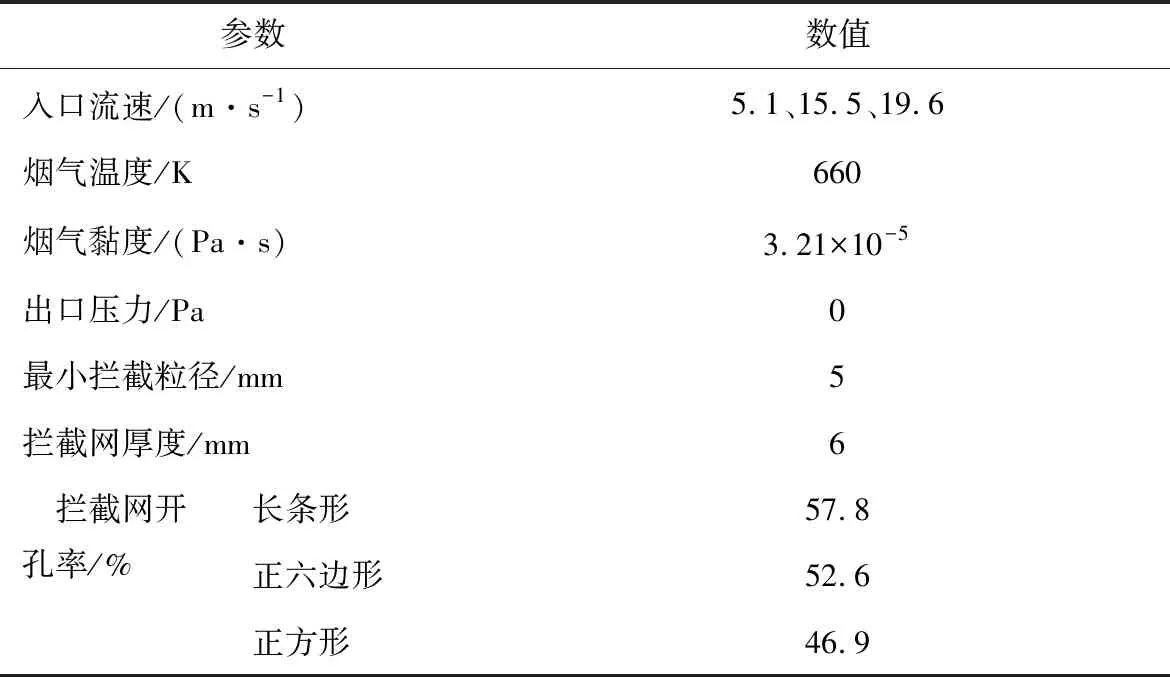
表1 模擬工況參數條件Table 1 Physical parameters for the simulations

1.2 控制方程

根據實際情況對模型做出如下簡化：來流煙氣為不可壓縮牛頓流體；煙氣在入口邊界處均勻分布且完全垂直于入口截面；煙氣之間的不同組分不發生化學反應，物性參數為常數。流體的控制方程包括連續性方程與動量方程，表達式為

ρ▽u=0，

(1)

ρ(u▽)u=▽(-pI+K)+F。

(2)

其中，ρ為流體密度，kg/m3；u為流體的速度矢量，m/s；p為微元流體上的壓強，Pa；I為單位矩陣；F為單位體積流體所受外力，N，本文只考慮流體所受重力，故F=ρg，g為重力加速度，m/s2；K為黏性應力，Pa，其表達式為

K=(μ+μT)(▽u+(▽u)T)。

(3)

其中，μ為流體動力學黏度，Pa·s；μT為湍流黏度，Pa·s，其表達式為

(4)

其中，Cμ為模型常數；k為湍動能，J；ε為湍動能耗散率。煙氣的流動狀態為湍流，研究選取典型的k-ε模型對其進行模擬。

2 結果與討論

入口氣流速度為15.5 m/s時，3種不同開孔形狀攔截網的速度分布與表觀壓力分布的截面圖如圖2所示，可知網孔后側存在高速區域，實體結構后側則存在一個低速區域。流場不均勻性在攔截網后側較短區域內逐漸衰減，最終流場變得均勻。不同開孔形狀的攔截網后側流場結構相似，可以推斷不同孔型攔截網對于煙氣整體流場影響規律接近。氣流表壓在攔截網前后產生明顯變化，在其他區域幾乎沒有變化。因此，計算域入口和出口的壓力差可以定義為攔截網壓降，后續對不同條件下的壓降規律進行詳細分析。

圖2 不同形狀攔截網速度與壓力分布云圖Fig.2 Velocity and pressure distribution of interceptor with different pore structures

2.1 開孔形狀對壓降的影響

3種攔截網在典型煙氣流速下的壓降情況見表2，其中流速大小5.1、15.5、19.6 m/s分別對應國內某600 MW燃煤鍋爐滿負荷工況下省煤器灰斗上方、水平緩流煙道、豎直煙道截面的平均流速。可知在最小攔截粒徑(即臨界尺寸)均為5 mm的條件下，壓降最大的是正方形攔截網，其次為正六邊形攔截網，壓降最小的是長條形攔截網。對比文獻[13]試驗結果，開孔率為48.5%～61.0%的平板式攔截網安裝在豎直煙道時(對應本文流速19.6 m/s的工況)，試驗壓降在169～414 Pa，二者在開孔率接近的工況點數據較為吻合，驗證了模擬結果的可靠性。不同開孔形狀攔截網在不同入口流速時的壓降變化如圖3所示，可知3種攔截網壓降均隨入口流速增大而增大，且在本文研究流速范圍內，仍符合長條形攔截網的壓降最小、正六邊形其次、正方形壓降最大這一規律，且隨著流速增大3者差別越明顯。

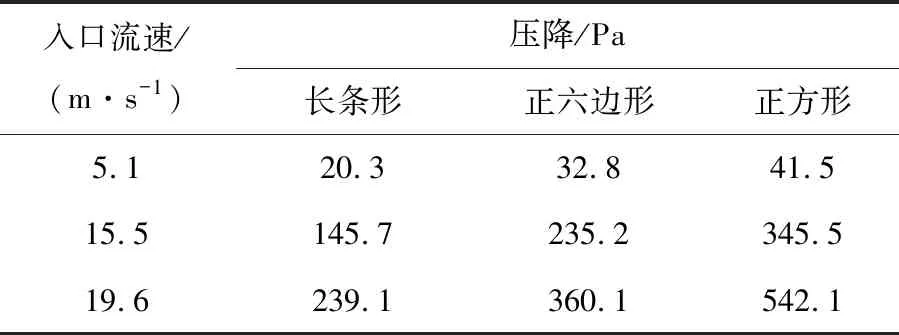
表2 典型流速下3種攔截網的壓降Table 2 Pressure drops of interceptors at typical flow velocities

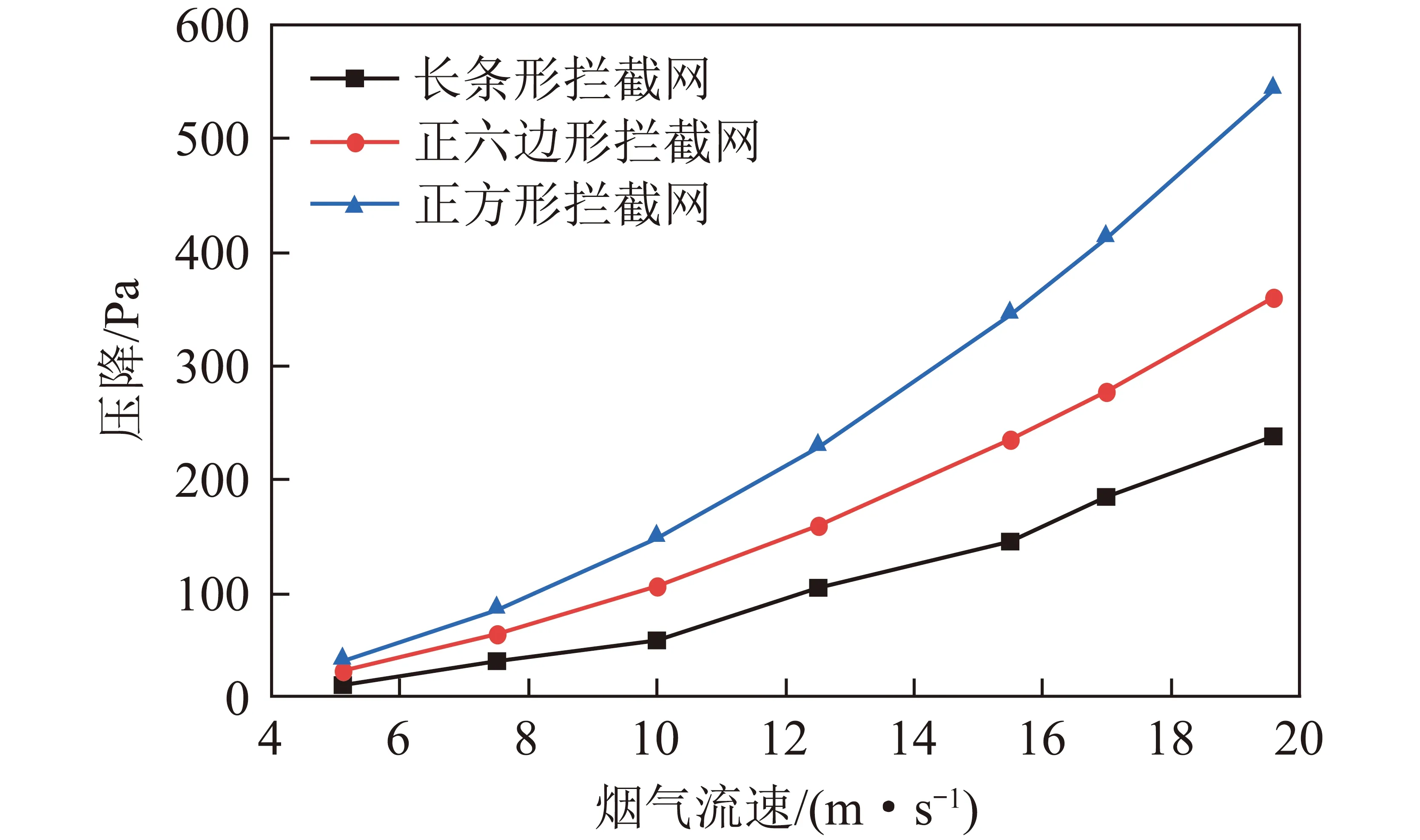
圖3 不同開孔形狀攔截網壓降與流速的關系Fig.3 Relationship between pressure drop and flow velocity of interceptor with different pore structures

分析認為造成長條形攔截網壓降小的原因是其開孔率較高。開孔率χ定義為網孔面積S0與攔截網總面積S的比值，是攔截網的重要設計參數，其表達式為

(5)

比較3種攔截網的開孔率(表1)可知，在相同攔截效果(即臨界顆粒尺寸相同)前提下，長條形攔截網開孔率最高，其次是正六邊形，正方形最小，這與攔截網壓降規律一致。又由于長條形攔截網的開孔率與其長寬比相關，保持流速不變進一步模擬了不同長寬比(開孔率)下的長條形攔截網的壓降情況見表3，證明長條形攔截網的壓降隨著長寬比(開孔率)增大而減小。

表3 長條形長寬比對開孔率及壓降的影響Table 3 Influence of length-to-width ratio on porosity and pressure drop

結果表明，開孔率與煙氣流速是影響壓降的重要因素，開孔形狀對壓降的影響可能源自開孔率的變化，下文將對開孔率及煙氣流速的影響進行定量描述。

2.2 開孔率和煙氣流速對壓降的影響

基于第2.1節結論，進一步探究開孔率對壓降的影響。通過改變開孔孔徑、相鄰網孔的距離等方式改變攔截網的開孔率χ，模擬計算3種孔型攔截網在不同開孔率(通過改變臨界尺寸實現)、不同流速下的壓降情況，如圖4所示。

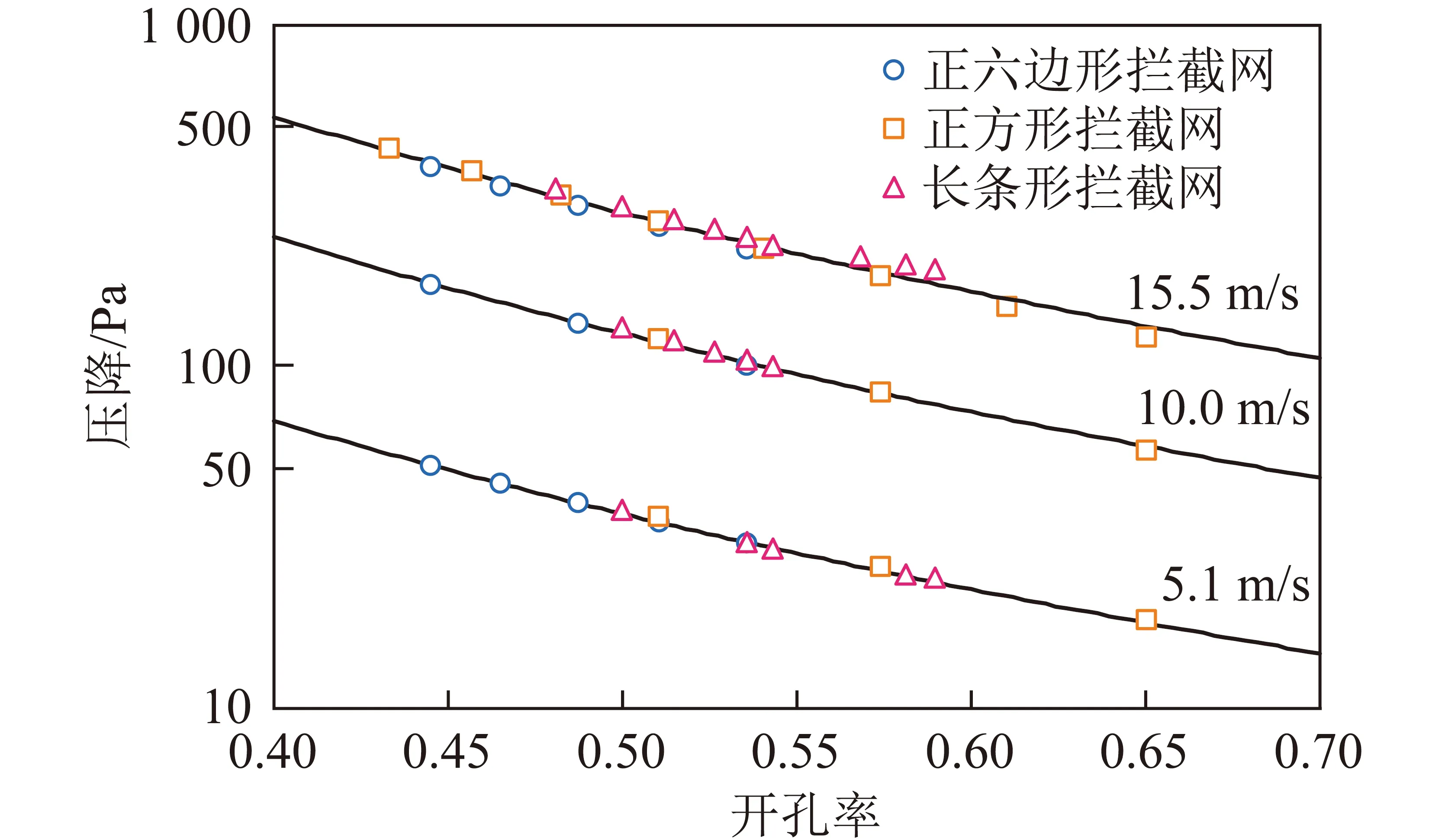
圖4 攔截網壓降與開孔率的關系Fig.4 Relationship between interceptor pressure drop and porosity

使用冪函數對相同流速下的數據點進行擬合，具體為

ΔP=Cχβ,

(6)

式中，ΔP為壓降，Pa；C為擬合系數，Pa；β為經驗常數。

可知3個流速下的擬合曲線決定系數分別為0.994、0.998、0.992。同一流速下不同開孔形狀的數據點均分布在同一條曲線附近，證明攔截網壓降主要與開孔率相關，開孔率越高壓降越小。在相同開孔率下，開孔形狀對攔截網壓降的影響幾乎可以忽略。不同流速下的壓降隨開孔率變化規律類似，流速增加會使壓降曲線上移。

根據以上結果，可以推斷出實際攔截網設計時，在確保攔截效果前提下，盡量選取開孔率較高的孔型(即長條形)，同時應綜合考慮結構強度、加工成本等因素后進行選型設計。

2.3 攔截網厚度對壓降的影響

為探究攔截網厚度對其壓降的影響，改變攔截網厚度n，計算入口流速5.1 m/s時3種孔型攔截網在不同開孔率下的壓降情況，如圖5所示(藍色、橙色和紅色代表厚度分別為6、12、18 mm)，曲線為n=6 mm的壓降擬合曲線。由圖5可知，隨厚度增加，相同開孔率攔截網的壓降均小幅增加。為了更清晰展示攔截網厚度的影響，選取開孔率為0.51的攔截網，繪制壓降隨厚度變化關系(圖6)。可知隨厚度增加，壓降呈準線性增加。在實際工程應用中，受限于加工難度和結構強度等，攔截網厚度變化范圍有限，與煙氣流速和開孔率相比，攔截網厚度對壓降影響較小。

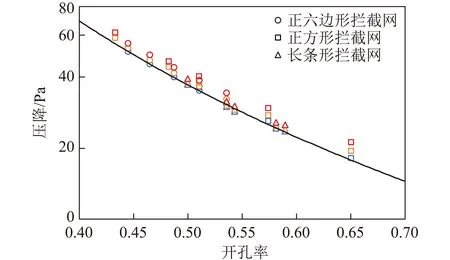
圖5 攔截網壓降與厚度的關系Fig.5 Relationship between pressure drop and thickness of interceptor

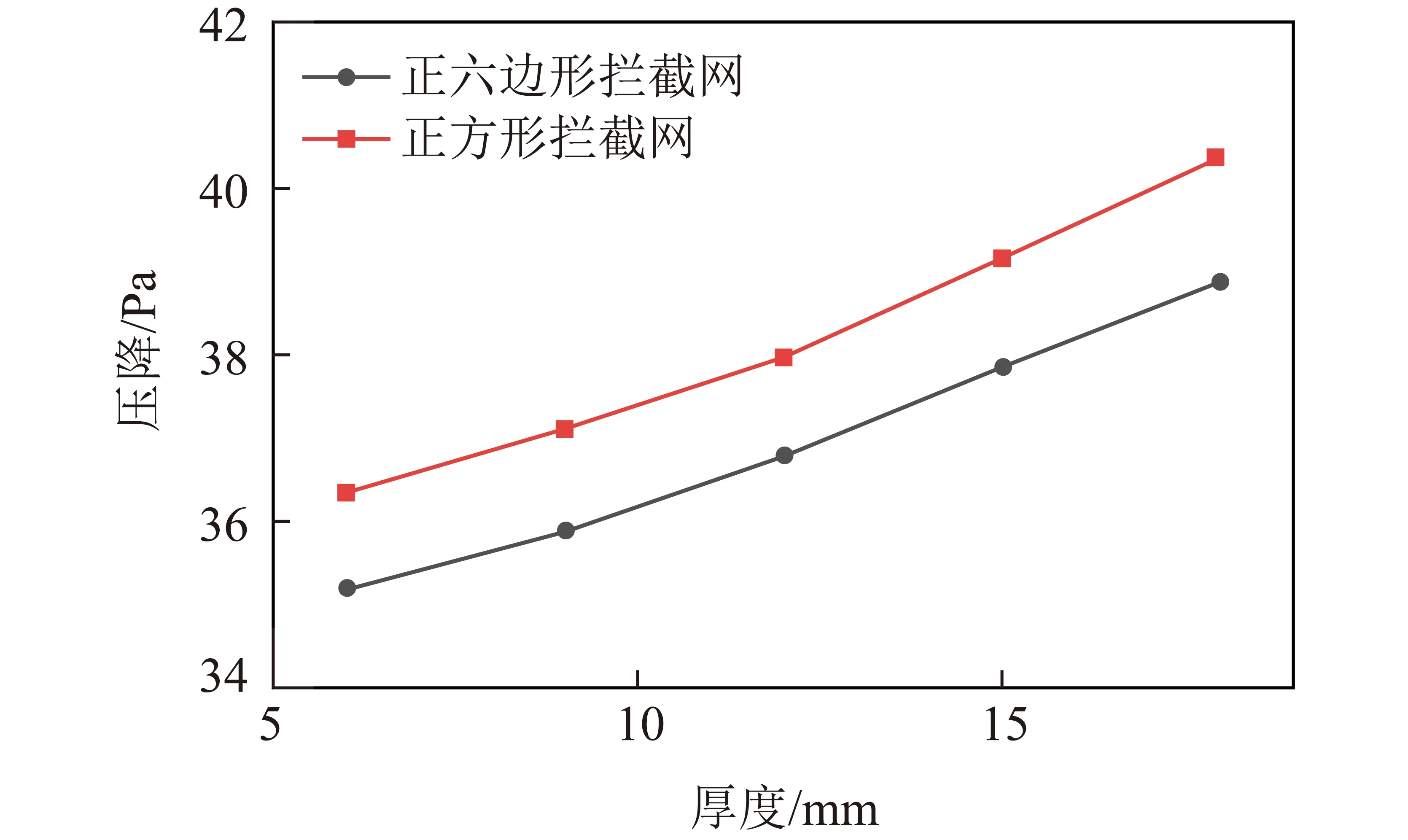
圖6 開孔率為0.51時，壓降隨厚度變化Fig.6 Change of pressure drop with thickness at the porosity of 0.51

2.4 壓降及滲透率關聯式

攔截網開孔率、厚度以及流速對攔截網壓降的影響可用冪函數的形式來量化，因此將攔截網壓降進行擬合：

ΔP=(An+B)uαχβ。

(7)

其中，u為攔截網區域煙氣流速，m/s；A、B、α均為經驗常數，A單位為Pa·sα·m-α-1，B單位為Pa·sα·m-α。對大量不同模擬工況下的數據點進行擬合，得到：

ΔP=(2.12n+0.24)u1.82χ-2.87。

(8)

可知式(8)的擬合決定系數為0.996，平均絕對百分比誤差為3.4%，擬合效果良好。已有研究報道攔截網阻力與其開孔率的3次方成反比[13]，即ΔP∝χ-3，這與式(8)規律接近，驗證了該擬合公式的可靠性。選取110個不同開孔形狀、煙氣流速、開孔率以及攔截網厚度組合工況，以模擬計算得到的壓降為橫坐標，以關聯式(8)預測壓降為縱坐標，將數據點繪制于圖7，當數據點位于y=x實線上時，表明公式預測與模擬結果吻合。可知所有數據點均位于±10%誤差范圍內(圖7虛線)，證明上述關聯公式在流速5～20 m/s、攔截網開孔率40%～65%、厚度6～18 mm的工況下可以綜合反映三者對壓降的影響。

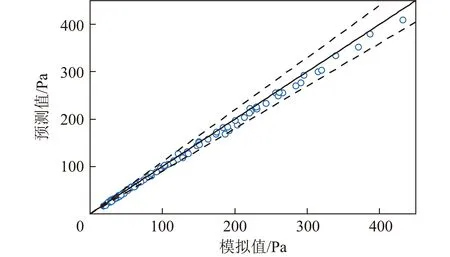
圖7 壓降公式預測值(式(8))與模擬結果值對比Fig.7 Prediction of pressure drop (Eq.(8))versus simulation results

對實際SCR系統進行CFD設計計算，通常采用多孔介質對攔截網進行等效模擬，即采用多孔介質代替具體的攔截網結構型式，基于攔截網開孔率和滲透率等宏觀參數可以求解出流場經過攔截網的壓力損失。滲透率kl的計算通常基于達西定律，具體為

(9)

其中，Q為單位時間滲流量，m3/s；L為滲流長度，m；A0為流體通過多孔介質的截面積，m2。該定律將流量、流體的物理性質及多孔介質的壓力梯度相聯系。將壓降公式代入基于達西定律的滲透率定義式，得到等效多孔介質滲透率kl為

(10)

以上擬合公式為預測攔截網壓降以及設備尺度CFD等效模擬提供基礎，具有一定參考指導意義。

3 結 論

1)影響攔截網壓降的主要因素為氣流速度和攔截網開孔率。流速5～20 m/s、開孔率40%～65%時，攔截網壓降約與煙氣流速的2次方成正比，與開孔率的3次方成反比。

2)攔截網壓降與開孔形狀無明顯關聯，不同攔截網開孔形狀對攔截網壓降的影響主要通過開孔率變化實現。在確保攔截效果前提下，應盡量選取開孔率較高的孔型(如大長寬比的長條形)。

3)攔截網厚度為6～18 mm時，壓降隨厚度增加呈準線性增加，但受限于工程實際應用，攔截網厚度可變范圍小，故其對壓降的影響也較小。

4)基于模擬數據，給出了冪函數形式的壓降預測公式，描述壓降與開孔率、流速、厚度之間的關聯，并進一步推導了攔截網等效多孔介質滲透率的經驗表達式，為攔截網的選型設計及全尺度模擬計算提供理論依據。