基于中法規范的連續實心板梁橋內力分析對比研究

黃 靖 張謝東 陳小佳 李 彬 劉建軍

(1.武漢理工大學交通與物流工程學院 武漢 430063； 2.中交第一公路工程局集團有限公司 北京 100024)

伴隨著中國基建力量的發展壯大，在海外特別是非洲地區承建了大量的公路橋梁[1-2]建設項目。非洲地區一些國家采用法國規范，與我國規范有較大差異，因此對比中法規范在橋梁設計上的差異具有重要意義。中國規范主要采用JTG D60-2015 《公路橋涵設計通用規范》[3]及JTG 3362-2018《公路鋼筋混凝土及預應力混凝土橋涵設計規范》[4]。法國規范主要采用《CAHIER DES CLAUSES TECHNIQUES GéNéRALES》(CCTG)[5-6],結構設計及驗算主要應用《Eurocode 2:Design of concrete structures》[7]。目前已有部分學者對法國規范的不同結構進行了設計分析[8-13]，但將中、法規范進行對比的研究工作還較少[14]。

文中以非洲某鋼筋混凝土連續實心板梁橋為研究對象，計算分析該梁橋的設計內力差異，通過驗算結構承載力來評價中、法規范的安全性差異，總結兩國規范在橋梁設計上的異同點，以期為后續非洲橋梁的設計、施工及養護提供參考。

1 研究背景

某鋼筋混凝土連續實心板梁橋，結構布置為跨徑12 m+17.6 m+17.6 m+12 m現澆鋼筋混凝土連續梁橋，邊跨梁長12 m，邊跨板支座間的距離(計算跨徑)L1c=11.5 m；中跨板支座間的距離(計算跨徑)L2c=17.6 m。橋面寬10.2 m，雙向兩車道布置，橫向采取結構雙向找坡，坡度為2.5%，板高由65.00 cm到77.75 cm變化。該橋的橫斷面結構圖見圖1。

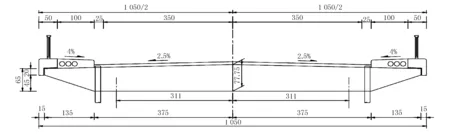
圖1 主橋橫斷面結構圖(尺寸單位：cm)

設計荷載：中國規范為標準的車道-I級荷載和人行道荷載3.0 kN/m2，法國規范為車道荷載Bc系列和人行道荷載1.5 kN/m2；材料：鋼筋混凝土梁采用C35混凝土，結構主筋采用Fe E400鋼筋。

2 中法規范結構設計對比

2.1 極限狀態對比

中、法2種規范均需要按正常使用極限狀態和承載能力極限狀態2種狀況對橋梁進行結構設計，2種規范規定的極限狀態見表1。由表1可知，從極限狀態定義來看，兩國的劃分標準幾乎一致，正常使用極限狀態均是從結構能達到正常使用條件來定義，承載能力極限狀態均是不發生明顯外形變化從而影響結構穩定的狀態。

表1 中法規范極限狀態對比

2.2 荷載對比

2.2.1恒荷載

中國規范：由JTG D60-2015 《公路橋涵設計通用規范》規定可知，在公路橋梁中恒載主要由結構自重、橋面鋪裝，以及附屬設備等附加力引起，橋梁結構設計的恒載為鋼筋混凝土或預應力混凝土自重，重度按26 kN/m3考慮。

法國規范：由CCTG中《Fascicule N°61_Titre V》規定可知，恒載重度一般為25 kN/m3，后續進行結構內力設計時也取用該值。但是自重存在最大和最小的特征值，是自重加上或減去根據結構或構件估計的標準分數及體積計算的近似程度來評估的，特征值為23.5～26.5 kN/m3，即相對于標準重度可上下浮動6%。

2.2.2人群荷載

中國規范人群荷載標準值與計算跨徑有關，對于跨徑不等的連續結構，以最大計算跨徑為準。對于非機動車及人行密集的公路橋梁，人群荷載標準值為規定標準值的1.15倍；對于專用人行橋梁，人群荷載標準值為3.5 kN/m2。

法國規范規定橋梁上的人行道承擔150 kgf/m2的均勻荷載，即人群荷載標準值恒定為4.5 kN/m2。中、法規范的人群荷載對比見表2。

表2 人群荷載對比

2.2.3汽車荷載

中國規范中的汽車荷載等級按公路等級來劃分。汽車荷載由車道荷載和車輛荷載兩部分組成，橋梁結構在整體計算采用車道荷載，局部計算時采用車輛荷載。法國規范在計算橋梁結構穩定性時一般主要考慮A、B 2種荷載類型，這2種系列荷載是相互獨立的，因此不能同時使用。汽車荷載等級分為3級，主要根據橋面寬度及作用來劃分。

對結構整體進行計算時，一般只考慮車道荷載，兩國規范車道荷載受汽車荷載等級、橫向車道布置等影響。中、法規范汽車荷載等級劃分見表3，橫向車道分布系數見表4～表6。

表3 汽車荷載等級對比

表4 中國規范的橫向分布系數

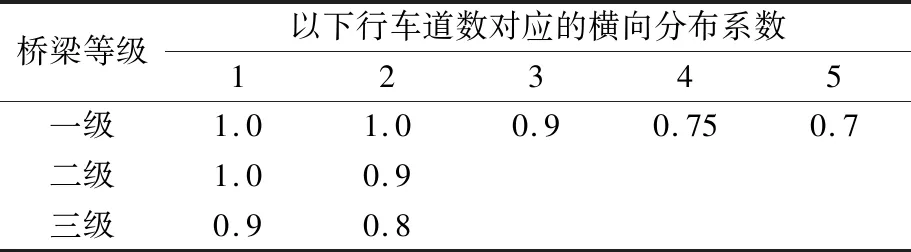
表5 法國A類荷載橫向分布系數

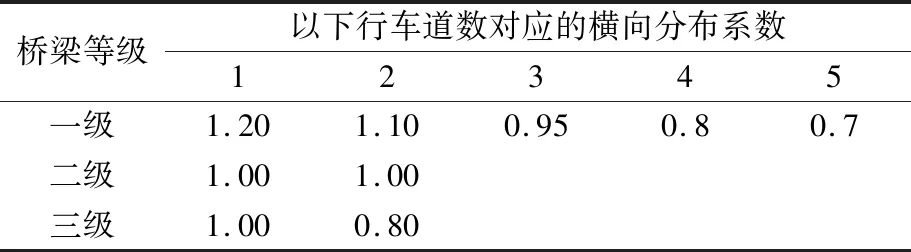
表6 法國B類荷載橫向分布系數

中國規范的車道荷載由均布荷載和集中荷載構成。均布荷載與集中荷載均跟汽車荷載等級有關，而集中荷載還與橋梁跨徑有關，在考慮剪力效應時，均布荷載需乘以1.2的放大系數，公路-II級車道荷載均按公路-I級車道荷載的0.75%取用。法國規范規定當一般橋梁跨徑小于200 m時，橋面承受的車道荷載為均布荷載，取值計算與橋梁等級和行車道數有關。由于該橋設計等級為公路-I級，因此中、法規范下的一級橋梁車道荷載計算對比結果見表7。

表7 車道荷載計算表

2.2.4荷載作用計算內力

為了對比中、法2種規范下結構的計算內力差異，通過計算得到恒、活荷載作用時不同規范下橋梁的跨中彎矩和支點剪力，對比結果見表8、表9。

表8 計算跨中彎矩對比 kN·m

表9 計算支點剪力對比 kN

由表8、9可知，在不同跨徑下，中、法規范中恒載產生的彎矩和剪力值相差不大，僅為4%，與兩國規范規定的恒載集度差異值一致。在汽車荷載作用下，中國規范下的計算跨中彎矩和支點剪力均大于法國規范；跨徑為11.5 m時，兩國規范下的跨中彎矩分別相差44%和31%；當跨徑增大到17.6m時，2種規范計算值的差異減小到24%和13%；兩國規范下邊跨支點剪力相差37%和25%，而中跨支點剪力只相差17%和6%。表明隨著跨徑的增大，在汽車荷載作用下兩國規范的計算結構內力差異在逐漸減小，小跨徑時中國規范的計算值偏大，跨徑增大到一定值后，法國規范的計算值偏大。因該橋跨徑較小，因此中、法規范中的人群荷載大小均不隨跨徑變化，法國規范下的計算彎矩和計算剪力始終為中國規范的50%。

2.3 荷載組合對比

2.3.1荷載組合

鑒于中、法規范對于荷載的規定存在差異，因此對于橋梁結構設計時不同極限狀態的荷載組合規定也不同，但是2種規范均是以恒載+汽車荷載+人群荷載的方式來定義荷載組合，兩國規范荷載組合對比見表10。

表10 中、法規范荷載組合對比

2.3.2極限狀態設計內力

由于法國規范中B類荷載更適用于本橋結構，因此選取表8、9 中B類荷載引起的計算內力為法規的計算內力，再結合表10中的荷載組合對比，計算可得極限狀態下兩國規范的計算跨中彎矩和支點剪力值，對比結果見表11、表12。

表11 計算跨中彎矩對比 kN·m

表12 計算支點剪力對比 kN

由表11、12可知，在承載能力極限狀態下，中國規范下的計算跨中彎矩比法國規范大5%～16%，支點剪力較法國規范增大1%～9%，但隨著跨徑的增大，兩國規范的設計值差異逐漸減小。在正常使用極限狀態下，中國規范的內力設計值較法國規范偏小，跨中彎矩值差異范圍為28%～43%，支點剪力值差異范圍為11%～26%，且隨跨徑增大差異值也在逐漸增大。

由上述分析可知，兩國規范中恒載差異較小，而對于活荷載的定義差異較大，在承載能力極限狀態下，兩國規定的荷載組合中活荷載系數值差異不大，因此計算內力值差異較小；而正常使用狀態下，法國規范下的荷載組合活荷載系數值大于中國規范，導致法國規范的計算內力值也大于中國規范。

3 中、法規范結構驗算對比分析

為了分析中、法規范在結構設計上的安全性與經濟性差異，定義一個變量稱為截面富余度，其含義是指截面的抗力值與內力值之比，富余度越大，說明截面的安全性越高。鑒于篇幅限制，下文部分公式以及示意圖中的符號含義不作詳細解釋。中國規范見JTG 3362-2018 《公路鋼筋混凝土及預應力混凝土橋涵設計規范》，法國規范見《Eurocode 2:Design of concrete structures》。

3.1 抗彎承載力驗算

兩國規范中受彎構件的正截面抗彎承載力驗算方法類似，截面受壓區均可簡化為矩形，且兩國規范的受彎構件截面受壓區簡化成矩形后的應力分布類似，鑒于該橋是一座非預應力連續實心板梁橋，因此中國規范下抗彎承載力應滿足式(1)規定。

(1)

法國規范抗彎承載力公式見式(2)，對于混凝土強度η及受壓區高度有效系數λ有取值規定，系數取值見式(3)。

(2)

(3)

根據上述公式，計算出抗彎承載力并對比見表13。

表13 抗彎承載力驗算對比

由表13可知，在跨徑為11.5 m時，兩國規范的截面抗彎富余度大小無明顯差異，而當跨徑為17.6 m時，中、法規范的截面抗彎富余度在逐漸減小，法國規范減小幅度更大。說明結構在跨徑較小時，兩國的抗彎富余度較為接近，而隨著跨徑增大，中、法規范抗彎富余度均在下降，法規的抗彎富余度降低幅度更大。

3.2 抗剪承載力驗算

由于該橋為實心板截面，且只配置了縱向普通鋼筋及箍筋，因此中國規范規定的斜截面抗剪承載力公式見式(4)。

Vcs=0.45×10-3α1α2α3bh0·

(4)

法國規范中對于帶有縱向抗剪鋼筋的混凝土構件，結構極限抗剪承載力為式(5)、(6)中的較小值。

(5)

(6)

兩國規范抗剪承載力計算結果見表14。

表14 抗剪承載力驗算對比

由表14可知，在跨徑為11.5 m時，中國規范的截面抗剪富余度要稍大于法國規范，而當跨徑為17.6 m時，中、法規范的截面抗剪富余度均發生明顯下降，分別降低了18%和23%。表明隨著跨徑增大兩國規范的結構設計抗剪能力均在降低，且法國規范的減小幅度大于中國規范。

3.3 裂縫寬度驗算

由于該橋為非預應力鋼筋混凝土結構，允許橋梁結構存在裂縫，但是需要進行裂縫寬度驗算來保證結構的強度要求。中國規范中裂縫寬度允許值是根據所處環境來劃分，而法國規范中裂縫寬度允許值是根據構件的暴露等級來劃分，兩國規范下裂縫寬度允許值對比見表15。

表15 裂縫寬度允許值對比 mm

由表15可知，該橋所處I類一般環境，按中國規范裂縫寬度允許值為0.2 mm；按法國規范規定的暴露等級劃分，該橋裂縫會對橋梁耐久性產生影響，因此裂縫寬度允許值為0.3 mm。

中國規范下對于鋼筋混凝土受彎構件的裂縫寬度計算公式如式(7)所示。

(7)

法國規范中裂縫寬度是通過相關荷載作用下產生的平均應變與不同裂縫之間混凝土平均應變的差值來計算的，最大值為裂縫寬度值，計算公式如式(8)所示。

(8)

兩國規范下裂縫寬度驗算對比結果見表16。

表16 裂縫寬度驗算對比

由表16可知，不同跨徑下法國規范的裂縫寬度計算值均大于中國規范，且2種規范裂縫計算值均小于允許值，表明2種規范設計下的結構強度均滿足要求。在跨徑為11.5 m時，法國規范的裂縫寬度容許值/計算值較中國規范小12%左右；隨著跨徑的增加，兩國規范的裂縫寬度容許值/計算值的大小均在減小，但法國規范的裂縫寬度容許值/計算值仍較中國規范小14%左右。表明中國規范在裂縫寬度計算與允許值規定方面較為保守，安全性更高。

4 結論

本文以非洲某連續實心板梁橋為例，對比分析了中、法橋梁設計規范之間極限狀態與設計荷載的差異，對該橋上部結構進行了設計內力的計算與驗算對比，得出如下結論。

1) 中、法規范對于交通荷載的定義有較大差異，因此在汽車荷載和人群荷載的作用下，中國規范計算的結構內力值要大于法國規范。且由于兩國規范規定的極限狀態下荷載組合系數的不同，導致中國規范的設計內力值在承載能力極限狀態下大于法國規范取值，而在正常使用狀態下小于法國規范取值。

2) 通過對結構的承載力驗算分析可知，中國規范的內力值和抗力值均大于法國規范取值，橋梁跨徑較小時，兩國規范的截面富余度差異不大，隨著橋梁跨徑的增大，這種差異值在逐漸增加，且兩國規范的截面富余度均在降低，法國規范降低幅度大于中國規范，表明中國規范的結構安全性大于法國規范，在保證相同安全儲備的情況下，中國規范所耗費的材料更少，經濟性更好。

3) 本文只對結構極限承載力進行了驗算對比，而兩國規范在正常使用極限狀態下的計算內力值差異更大，可以進一步對該狀態下的結構內力進行驗算，以對比分析中、法規范在結構正常使用狀態下的設計差異。