DK SPACES AND CARLESON MEASURES*
Dongxing LI (李東行)
School of Financial Mathematics and Statistics,Guangdong University of Finance,Guangzhou 510521,China
E-mail:47-075@gduf.edu.cn
Hasi WULAN (烏蘭哈斯)
Department of Mathematics,Shantou University,Shantou 515063,China
E-mail:wulan@stu.edu.cn
Ruhan ZHAO (趙如漢)?
Department of Mathematics,SUNY Brockport,Brockport,NY 14420,USA
E-mail:rzhao@brockport.edu
Abstract We give some characterizations of Carleson measures for Dirichlet type spaces by using Hadamard products.We also give a one-box condition for such Carleson measures.
Key words DK space;Hadamard product;mean growth;Carleson measure
1 Introduction
Let D={z∈C:|z|<1}be the unit disk,let?D={z∈C:|z|=1}be the unit circle,and let Hol (D) be the space of all analytic functions on D.Fora,z∈D,letbe the Mbius transformation on D that interchangeszanda.It is known that the Green function of D with logarithmic singularity ata∈D is given byg(z,a)
For 0<p≤∞,the mean growth of functionfon D is defined as
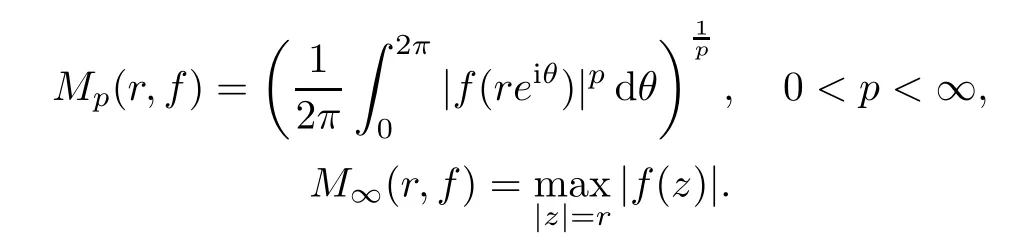
The Hardy spaceHpconsists of those functionsfthat are analytic on D for which

For 0<p<∞andα>-1,the weighted Bergman spaceconsists of thosef∈Hol (D) such that

The weighted Dirichlet space(0<p<∞,α>-1) consists of thosef∈Hol (D) such thatf′∈.Hence,iffis analytic in D,then

The classical Carleson measure was introduced by Carleson[8]in his solution to the corona problem.We say that a positive Borel measureμon D is a Carleson measure if the embedding operator from the Hardy spaceHpintoLp(dμ) is bounded;that is,there is a positive constantCsuch that

for allf∈Hp.There is a simple geometric characterization of these measures.
For an arcI??D,let|I|denote the normalized arc length ofIso that|?D|=1.We call
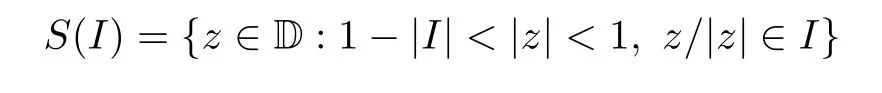
a Carleson box.It is well-known that a positive measureμon D is a Carleson measure if and only if there exists a constantC>0 such thatμ(S(I))≤C|I|for allI??D.Ifa=(1-|I|)eiθis the midpoint of the inner side of the Carleson box;we will also denoteIbyIaandS(Ia) byS(a).
We may extend the notion of the Carleson measure by replacing the right-hand side of (1.1) by the norm or the semi-norm of some other function space such as the Bergman space,the Bloch space,or the BMOA,etc..In general,if we letXbe a space of analytic functions on D,for 0<p<∞,a positive Borel measureμon D is said to be ap-Carleson measure for the spaceXif the embedding mapI:XLp(dμ) is a bounded operator,i.e.,there is a constantC>0 such that

for all functionsf∈X.When the parameterp=2,we always simply leave out thepin front of the Carleson measure.The following result is due to Wu:
Proposition 1.1([16]) Suppose that 0<p≤2,and letμbe a positive Borel measure on D.Thenμis ap-Carleson measure forif and only ifμis a classical Carleson measure.
Ifs>0 andμis a positive Borel measure on D,we can generalize the classical Carleson measure by saying thatμis ans-Carleson measure on D if there exists a positive constantCsuch thatμ(S(I))≤C|I|sfor any intervalI??D.Note that the following two notations are different:
(i)μis ap-Carleson measure on D;
(ii)μis ap-Carleson measure for a spaceX.The following results are known:
Proposition 1.2([13]) Assume that 0<p<∞,thats>1,and letμbe a positive Borel measure on D.Thenμis ans-Carleson measure on D if and only ifμis ap-Carleson measure for
Proposition 1.3([15]) Suppose that 0<s<∞.Ifμis a Carleson measure forDs,thenμis ans-Carleson measure.In particular,fors≥1,μis a Carleson measure forDsif and only ifμis ans-Carleson measure.Fors=0,ifμis a Carleson measure forD,then
For a right continuous and nondecreasing functionK:[0,∞)[0,∞),we define the weighted Dirichlet spaceDKof analytic functionsfon D such that
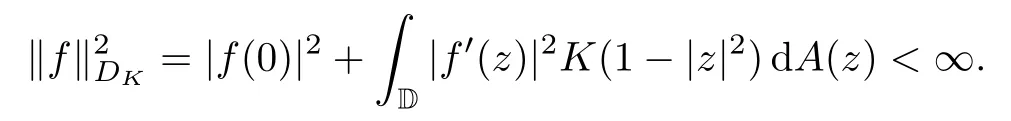
ForK(t)=ts,0<s<∞,we have thatDK=Ds.
By Theorem 2.1 in[10],we may assume thatKis defined on[0,1];we may extend its domain to[0,∞) by settingK(t)=K(1) fort>1.Furthermore,we need the two following conditions onK:

Note that (1.3) implies the ensuing doubling condition;that is,there exist positive constantsCandMsuch that

Also,by Theorem 5 in[17](see also Theorem 3.8 in[18]),we know that ifKsatisfies condition (1.3),then

Suppose thatKsatisfies (1.3).Then,we see thatKalso satisfies (1.4) and (1.5).By a proof similar to the one for Theorem 2.18 in[18],we know that in this case,an analytic functionfon D is inDKif and only if

2 Carleson Measure With Hadamard Products

By Parseval’s formula,(1.6),and Theorem 6 in[17],we get
Proposition 2.1Suppose thatKsatisfies (1.2) and (1.3).Thenf∈DKif and only iff*g∈H2,where
Aulaskari,Girela and Wulan gave the following characterization of a Carleson measure by using Hadamard products:
Proposition 2.2([4]) For 0<s<∞,a positive Borel measureμdefined on D is a classical Carleson measure if and only if there exists a positive constantCsuch that

One of our goals is to extend these results to thes-Carleson measure and toDKspaces.We need the following result:
Lemma 2.3([9]) Let 0<s<∞.A positive Borel measureμon D is ans-Carleson measure if and only if

Theorem 2.4Suppose thatKsatisfies conditions (1.2) and (1.3).A positive Borel measureμon D is ans-Carleson measure fors≥1 if and only if there exists a constantC>0 such that

Proof“?”.Then,by Proposition 2.1,we know that
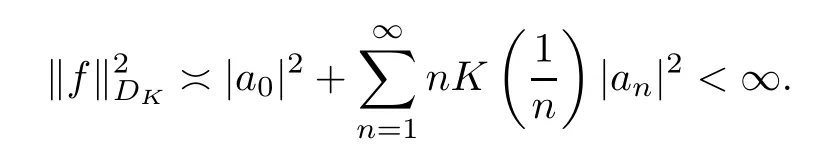
Using this equation and (1.3) of[4],we get that

is equivalent to
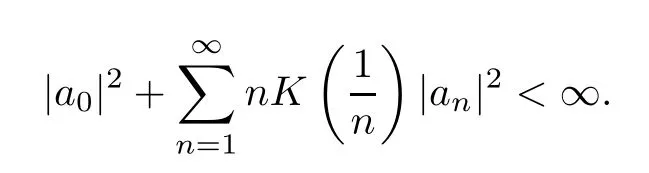
This gives that
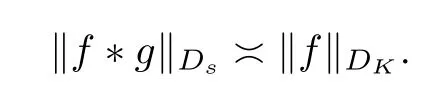
By Theorem 1.2 in[15]we know thatμis ans-Carleson measure withs≥1 if and only ifμis a Carleson measure forDs.Hence,we have that

“?”Conversely,suppose that (2.1) holds for allf∈DK.For eacha∈D with|a|>,we take the testing function

By Proposition 2.1,we have that

Since,forp>0,we have that

by Stirling’s formula

we get that

On the other hand,


From (2.1) and the inequality,it follows that

By Lemma 2.3,we know thatμis as-Carleson measure. □
Theorem 2.5Suppose thatKsatisfies condition (1.3).A positive Borel measureμon D is ans-Carleson measure fors>1 if and only if there exists a positive constantCsuch that

Proof“?”Suppose thatμis ans-Carleson measure.Let
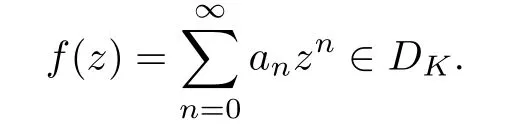

“?”Conversely,suppose that (2.3) holds for allf∈DK.For eacha∈D with|a|>we take the testing function

Therefore,

Combining the above inequalities and (2.3),we obtain that
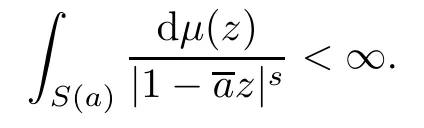
By Lemma 2.3,this means thatμis as-Carleson measure. □
3 One-Box Conditions for Carleson Measures
The classical Carleson one-box conditionμ(S(I))=O(|I|) can be generalized asμ(S(I))=O(φ(|I|)) by providing a nondecreasing functionφ:(0,1]→(0,∞).It is proved in[12]that a finite positive Borel measureμon D is a Carleson measure forDif it satisfies the Carleson one-box condition

whereφ:(0,1](0,∞) is an increasing function such that
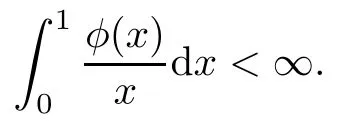
A Hilbert spaceHhas a reproducing kernelkw(z)=k(z,w) in the sense that
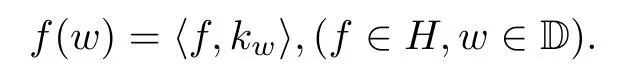
The following result is known:
Proposition 3.1(Lemma 24 of[2]) Assume that a Hilbert spaceHhas a reproducing kernelk(z,w).Letμbe a finite positive Borel measure on D.Then

From this result we immediately obtain the following characterization of a Carleson measure forH:
Corollary 3.2A finite positive Borelμon D is a Carleson measure for Hilbert spaceHwith a reproducing kernelk(z,w) if and only if

By the Cauchy-Schwartz inequality and the fact that|k(z,w)|=|k(w,z)|,we have that
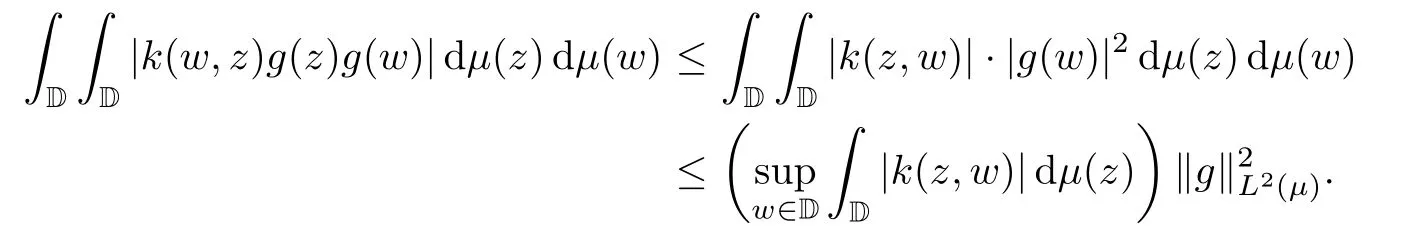
Therefore we get
Corollary 3.3A finite positive Borel measureμon D is a Carleson measure for Hilbert spaceHwith a reproducing kernelk(z,w) provided that
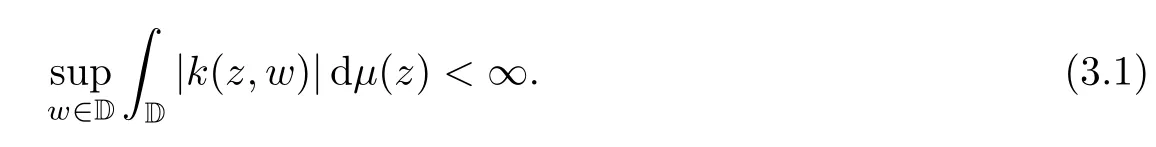
As an extension of a result of[12],we have the following theorem:
Theorem 3.4Lets>0,and letμbe a finite positive Borel measure on D satisfyingμ(S(I))=O(φ(|I|)),whereφ:(0,1](0,∞) is an increasing function such that

Thenμis a Carleson measure forDs.
ProofWe mainly follow the proof of Theorem 1.1 of[12].It suffices to show that (3.1) holds.In establishing (3.1),we can restrict our attention to thosewwith<|w|<1,since the supremum over the remainingwis clearly finite.
LetkDs(z,w) be the reproducing kernel forDs.The following estimate is well-known:

see,for example,page 28 in[3].
Fixwwith<|w|<1.By (3.3),using Fubini’s theorem to integrate by parts,we have that


is not void whent>1-|w|and Ωt=D whent≥1+|w|.Letw=reiθ.By a geometric consideration,we can prove that Ωt?S(It),whereItis the arc on?D centered ateiθwith normalized arc length
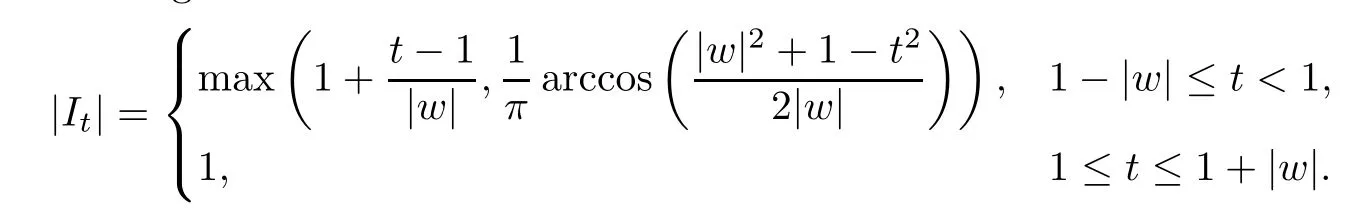
It can be easily shown that for 1-|w|≤t<1,
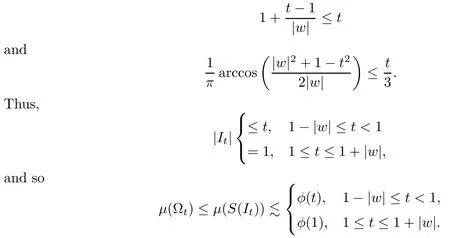
Therefore,by our condition in the theorem,we get that

By Corollary 3.3 we know thatμis a Carleson measure forDs. □
We give two examples here to illustrate this result.The first example gives an application of Theorem 3.4.
Example 3.5Let 0<s<1 and letβ>1.Let.It is proved by Pau and Pel′aez in Lemma 2.1 in[14]that ifμis a finite positive Borel measure on D satisfyingμ(S(I))=O(φ(|I|)),thenμis a Carleson measure forDs.It can be easily checked thatsatisfies condition (3.2).Hence,the above result of Pau and Pel′aez is an easy consequence of Theorem 3.4.
The next result shows that the result in Theorem 3.4 is in some sense sharp.
Example 3.6For any 0<s<1,there exists an increasing functionφon (0,1] such thatis strictly decreasing and

and there exists a finite positive Borel measureμon D satisfyingμ(S(I))=O(φ(|I|)) such thatμis not a Carleson measure forDs.
To prove this result,we need the concept ofQsspaces,which was introduced in[5].There are several equivalent definitions ofQsspaces;here we adopt a definition using Carleson measures.
Letting 0<s<∞,we say that an analytic functionfon D is in the spaceQsif dμf(z):=|f′(z)|2(1-|z|2)sdA(z) is ans-Carleson measure on D (see Theorem 1.1 in[6]).Relating to this paper,the concept ofQsspaces has been generalized toQKspaces using the weight functionKdiscussed above.Please see[7,19]and[20]for some more information aboutQKspaces and some other generalizations ofQsspaces.
In Corollary 2.1 in[1],Aleman,Carlsson and Persson proved that for everys∈(0,1),there exist functionsf∈Qs,g∈Dssuch that

Note that the last condition is equivalent to the fact that the measure dμf(z):=|f′(z)|2(1-|z|2)sdA(z) is not a Carleson measure forDs.
Back to Example 3.6.For any 0<s<1,letφ(t)=ts.Then,obviously,φsatisfies all the conditions in Example 3.6.Letfbe the function in Aleman,Carlsson and Persson’s example above,and let

Sincef∈Qs,we know that dμfis ans-Carleson measure,or thatμf(S(I))=O(φ(|I|)) forφ(t)=ts.However,dμfis not a Carleson measure forDs,hence we know that Example 3.6 is true.
Finally,as a corollary to Theorem 3.4,we get the following one-box condition for Carleson measures onDKspaces:
Corollary 3.7Suppose thatKsatisfies condition (1.3).Letμbe a finite positive Borel measure on D satisfyingμ(S(I))=O(φ(|I|)),whereφ:(0,1](0,∞) is an increasing function such that

Thenμis a Carleson measure forDK.
ProofIt is proved in[11,Lemma 2.2]that if (1.3) holds,then there is a weight functionK*,comparable toK,such thatK*(t)/tis decreasing for 0<t<∞.Thus,DK=DK*,and since

for 0<t≤1,we know thatDK?D1.By Theorem 3.4,we know thatμis a Carleson measure forD1,and hence also a Carleson measure forDK.The proof is complete. □
 Acta Mathematica Scientia(English Series)2022年3期
Acta Mathematica Scientia(English Series)2022年3期
- Acta Mathematica Scientia(English Series)的其它文章
- A ROBUST COLOR EDGE DETECTION ALGORITHM BASED ON THE QUATERNION HARDY FILTER*
- CONTINUOUS SELECTIONS OF THE SET-VALUED METRIC GENERALIZED INVERSE IN 2-STRICTLY CONVEX BANACH SPACES*
- EXISTENCE RESULTS FOR SINGULAR FRACTIONAL p-KIRCHHOFF PROBLEMS*
- BOUNDS FOR MULTILINEAR OPERATORS UNDER AN INTEGRAL TYPE CONDITION ON MORREY SPACES*
- LEARNING RATES OF KERNEL-BASED ROBUST CLASSIFICATION*
- A COMPACTNESS THEOREM FOR STABLE FLAT SL (2,C) CONNECTIONS ON 3-FOLDS*
