考慮兩階段運輸的加工資源共享調度策略

鄭斐峰， 靳凱媛， 宋沁睿， 劉 明

(1. 東華大學 旭日工商管理學院， 上海 200051；2. 同濟大學 經濟與管理學院， 上海 200092)

在共享經濟環境下，跨企業的共享加工模式能夠提高企業資源利用率，并解決生產領域資源結構性矛盾以及資源短缺與閑置浪費并存的難題[1]。文獻[2-5]描述了制造行業分享經濟的概念，并從加工資源平臺角度探討了資源分享的益處。對于服裝制造供應鏈而言：在傳統的加工模式下，某客戶訂單所需的原材料由相應的供應商運輸至指定服裝制造商處，再由制造商完成加工并將成品運送給客戶。該指定制造商與供應商及客戶的運輸距離相比其他制造商都是最近的。在分享加工模式下，某客戶訂單可能由多個供應商提供原材料，由多個制造商進行產品加工和成品配送，即同一客戶的訂單可以拆分成多個子訂單，并分配給不同制造商進行同步加工。分享加工模式可有效解決不同制造企業的資源利用不均衡問題。

目前，考慮加工與運輸環節的研究多針對非共享環境下的調度優化決策。文獻[6-8]同時考慮了加工環節與運輸環節的平行機調度問題。Yaghin等[9]研究不確定性條件下全球范圍內的實體供應渠道集成決策，包括供應商選擇、訂單分配和運輸計劃，建立多目標混合整數線性規劃模型以優化總物流成本、延遲時間和采購價值，提出一種帶效用函數的模糊多選擇目標規劃模型,用以解決多目標規劃問題。Kim等[10]研究具有相同任務處理時間、交付時間和成本的雙層平行機調度問題，分別以最小化總加權完成時間和車輛總交付成本之和,以及最小化總延遲和車輛總交付成本之和為目標，提出最佳調度和運輸交付策略。Jiang等[11]研究具有不同處理時間和尺寸的平行機調度問題，構建了以最小化完工時間為目標的混合整數規劃模型，并設計了離散粒子群優化算法和遺傳算法相結合的混合算法。Li等[12]考慮動態的供應商選擇和訂單分配，提出一種新的兩階段綜合數學模型。

部分文獻研究以完工時間為主要優化目標進行建模與分析。蘭艷等[13]針對帶運輸機的流水車間調度問題，以最小化所有工件運往目的地的時間為目標設計了不同情形下的最優算法。Hu等[14]研究考慮機器具有維護時間間隔的訂單交付協調的調度問題，針對最小化完成時間的優化目標提出了近似算法。Liu[15]考慮在電子制造業中具有p-s-d交付時間和學習效應的同型機調度問題，針對最小化總完成時間的絕對偏差、最小機器總負載，以及最小化總完成時間為優化目標的模型設計了多項式時間算法。薛梅等[16]提出批處理機環境下生產與兩階段運輸的協同調度問題，根據問題進行系統建模并引入交叉和變異算子改進粒子群算法，對制造跨度時間進行優化。

總體而言，當前文獻僅考慮成品配送的單個運輸階段，涉及上游原材料配送的兩階段運輸模型的研究較少，鮮有考慮加工資源分享下的生產與兩階段運輸情形。本文研究加工資源可分享環境下生產與兩階段運輸的協同調度問題，著重考察加工資源共享對客戶訂單完工時間的影響，即以優化所有訂單的總完工時間為目標，通過與資源無分享的傳統加工模式進行對比，從理論角度闡述分享加工模式在供應鏈服務時間方面的優勢。

1 問題描述與基本定義

1.1 問題描述

考慮一個由原材料供應商、制造商以及客戶組成的訂單加工與兩階段配送供應鏈網絡，即完成1個客戶訂單包括前后2個運輸環節和1個加工環節。考慮在加工資源通過共享平臺進行分享的加工模式下，對客戶的訂單進行合理拆分以使多個制造商同步加工，從而最小化訂單的總完工時間。對比分析加工資源無分享的傳統加工模式與分享加工模式的優劣。著重探討以下兩種供應鏈網絡：(1)1個供應商、2個制造商與1個客戶；(2)2個供應商、2個制造商與2個客戶。每個客戶i只提出一個訂單需求Ji，并且訂單i的原材料供應商是唯一確定的，因此，用相同的索引i表示該訂單對應的供應商。同時，作出如下假設：

(1)所有訂單在零時刻釋放，即訂單所需原材料可以在零時刻從供應商運往制造商。

(2)訂單加工完成后成品無需等待，立即運送給客戶。

(3)任意供應商與制造商、制造商與客戶之間的運輸時間均是已知常數，并且供應商i距離制造商m=i最近，制造商m=i距離客戶i最近，i=1,2。

(4)在兩種加工模式下，客戶訂單Ji所需的原材料只由供應商i提供。在傳統加工模式下制造商m只加工客戶i=m的訂單Ji，而在分享加工模式下制造商可以加工客戶i=m或者i≠m的訂單。

(5)所有制造商具有相同的加工速度，采用先到先服務(first-come-first-serve，FCFS)規則加工客戶訂單，且訂單加工過程無中斷。

1.2 參數及含義解釋

i為訂單以及對應的客戶與供應商的索引，i∈{1,2}；

m為制造商的索引，m∈{1,2}；

pi為訂單Ji的加工時間，i∈{1,2}；

pim為訂單Ji劃分給制造商m的子訂單Jim的加工時間，其中，pi1+pi2=pi，i∈{1,2}；

tim為訂單Ji的原材料到達制造商m處后等待啟動加工的時間，i,m∈{1,2}；

Lim為原材料從供應商i到制造商m的第一階段運輸時間，i,m∈{1,2}；

Hmi為成品從制造商m到客戶i的第二階段運輸時間，m,i∈{1,2}；

Cbi為訂單Ji的完成時間，b=1表示傳統加工模式，b=2表示分享加工模式，i∈{1,2}。

在兩種加工模式下，訂單Ji(i=1,2)的成品送達客戶的時間可表示為

Cbi=maxm∈{1,2}{Lim+pim+tim+Hmi}

(1)

顯然，當b=1時，有m=i，pim=pi且tim=0。考慮最小化所有客戶訂單總交貨時間的優化目標，用經典的三參數標記法將問題記為Pn|b|∑Cbi，Pn為平行機。

2 單客戶的加工配送情形

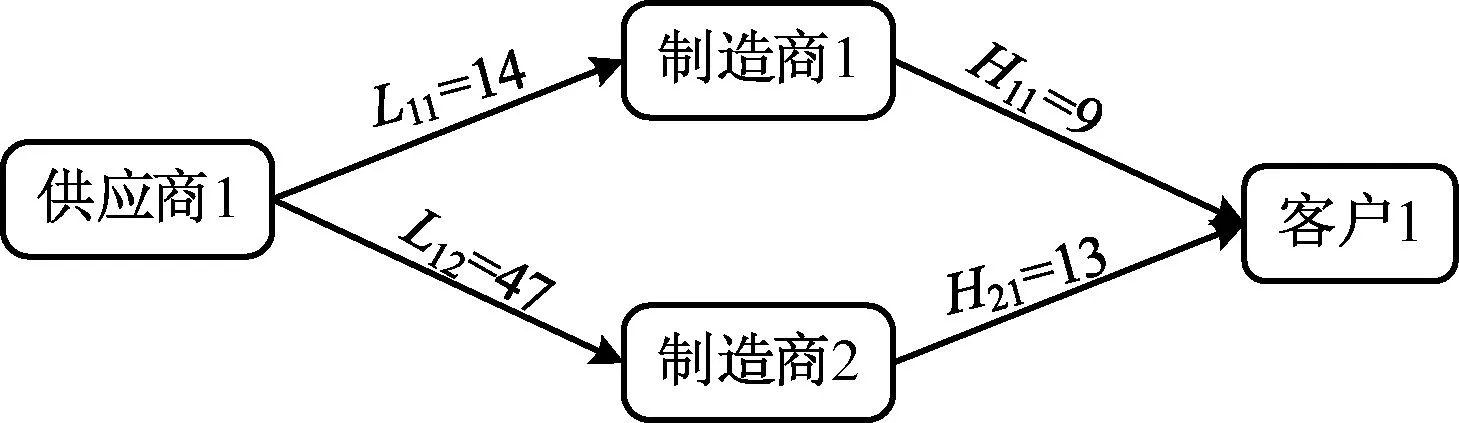
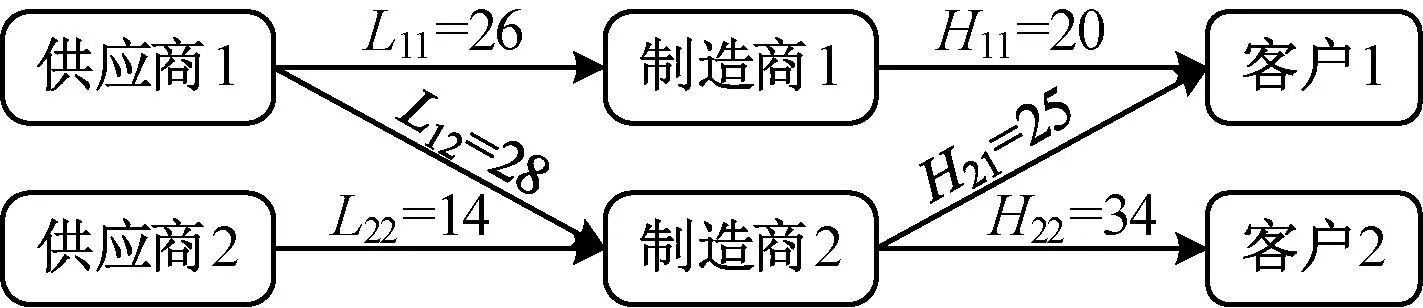
對于由1個供應商、2個制造商和1個客戶組成的供應鏈：根據假設(3)，L11

圖1 單個客戶時兩種加工模式下的訂單加工配送流程Fig.1 Processing and distribution flow in the two manufacturing modes with single customer order

在傳統加工模式下，t11=0。結合式(1)與假設(4)，訂單J1的完成時間C11為

C11=L11+p1+H11

(2)

在分享加工模式下，在制造商1、2完成交付子訂單J11和J12的時間分別為C211和C212，且訂單J1的完成時間C21=max{C211,C212}。令Δ1=(L12+H21)-(L11+H11)，根據假設(3)有Δ1≥0。

定理1：若p1>Δ1，分享加工模式優于傳統加工模式，且最優分享策略為p11=(p1+Δ1)/2，p12=(p1-Δ1)/2；反之，若p1≤Δ1，則分享加工模式的最優策略退化為傳統加工模式，即p11=p1。

證明：首先，傳統加工模式下的目標函數如式(2)所示。討論兩種情形p1>Δ1和p1≤Δ1時分享加工模式下的目標函數。

情形1：p1>Δ1

在分享加工模式下，子訂單J11的原材料由供應商1運輸至制造商1處，子訂單J12的原材料由供應商1運輸至制造商2處。根據式(1)，該模式下訂單J1的完成時間為

C21=max{L11+p11+H11,L12+p12+H21}

(3)

結合p1=p11+p12和情形1的條件p1>Δ1，令制造商1、2加工的子訂單時間滿足p11-p12=Δ1，即L11+p11+H11=L12+p12+H21，則C21=L11+p11+H11。由于p11=Δ1+p12

情形2：p1≤Δ1

情形2的條件等價于p1≤(L12+H21)-(L11+H11)，結合式(2)可得C11≤L12+H21。由式(3)可知，C21≥L12+H21≥C11。因此，分享加工模式下的最優策略為p12=0,p11=p1，即退化為傳統加工模式。綜上，定理1成立。

以圖2為例解釋定理1。Δ1=(L12+H21)-(L11+H11)=37，訂單J1的加工時間p1=50。

圖2 定理1中p1>Δ1的例子Fig.2 Example of p1>Δ1 in theorem 1

因為p1>Δ1，根據定理1的最優分享策略，p11=(p1+Δ1)/2=43.5，p12=(p1-Δ1)/2=6.5。

因此分享加工模式下的目標函數值為C21=L11+p11+H11=66.5，而傳統加工模式下的目標函數值C11=L11+p1+H11=73，表明前者優于后者。

3 雙客戶的加工配送情形

對于2個供應商、2個制造商和2個客戶的情形，根據假設4：在傳統加工模式下，制造商m(m=1,2)只加工客戶i=m的訂單Ji，加工配送流程圖如圖3(a)所示；在分享加工模式下，客戶i(i=1,2)的訂單Ji由原材料供應商i運送給制造商1和制造商2分別進行加工，完工后成品再交付給客戶i，加工配送流程如圖3(b)所示。

圖3 雙客戶時兩種加工模式下的訂單加工配送流程Fig.3 Processing and distribution flow in the two manufacturing modes with two customer orders

根據假設(3)，有L11

3.1 FCFS規則及目標函數分析

基于FCFS規則的加工策略如下：

Step 1 將訂單Ji(i=1,2)拆分成2個子訂單Ji1,Ji2，其原材料同時從供應商i處運往2個制造商處。

Step 2 由于L11

Step 3 制造商1完成子訂單J11后，再加工由供應商2提供原材料的客戶2的子訂單J21；同理，制造商2完成子訂單J22后，再加工由供應商1提供原材料的客戶1的子訂單J12。

給出兩種加工模式下基于制造商上述加工策略的目標函數表達式。客戶1的訂單類似于單客戶的加工配送情形，傳統加工模式和分享加工模式下客戶1的訂單完工時間分別如式(4)和(5)所示。

C11=L11+p1+H11

(4)

C21=max{L11+p11+t11+H11,

L12+p12+t12+H21}

(5)

在式(5)中根據FCFS規則加工策略的Step 2，制造商1先加工客戶1的子訂單J11，J11的等待時間為0，即t11=0。對于客戶1的另一個子訂單J12，J12的等待時間t12取值存在兩種情形：

情形1：子訂單J12在制造商2加工完成J22后到達制造商2處，即L12>L22+p22，則子訂單J12無需等待，即t12=0。此時，J12的完成時間為L12+p12+H21。

情形2：子訂單J12在制造商2加工完成J22前到達制造商2處，即L12≤L22+p22，則子訂單J12需等待的時間為t12=L22+p22-L12。此時，J12的完成時間為L12+p12+t12+H21=L22+p22+p12+H21。

上述兩種情形下訂單J1的完工時間整理如下：

(6)

類似定理1的分析，雙客戶情形下的最優分享策略：

當L12>L22+p22時，L11+p11+H11=L12+p12+H21或p11=(p1+Δ1)/2，p12=(p1-Δ1)/2；當L12≤L22+p22時，有L11+p11+H11=L22+p22+p12+H21。

同理，得到客戶2的訂單J2在兩種加工模式下的完成時間，如式(7)和(8)所示。

C12=L22+p2+H22

(7)

(8)

對于傳統加工模式，2個客戶的訂單J1和J2的總完工時間為

C11+C12=L11+p1+H11+L22+p2+H22

(9)

3.2 分享加工模式的占優情形分析

首先，證明同時拆分加工2個客戶的訂單時，不存在分享加工策略占優的情形。

定理2：同時拆分客戶1和客戶2的訂單J1,J2給兩個制造商加工時，不存在分享方案優于傳統加工方案的情形。

證明：反證法。兩個訂單同時分享(p11,p12,p21,p22>0)時，假設存在分享加工方案優于傳統加工方案的情形，即滿足不等式C21+C22L22+p22的情形。此時，訂單J1的子訂單J12在制造商2處加工無需等待。如果L11+p11+H11>L12+p12+H21，則減小p11、增大p12可以降低分享加工模式下的C21。因此，假設L11+p11+H11≤L12+p12+H21。同理分析式(6)中L12≤L22+p22的情形以及式(8)，可將式(6)和(8)簡化為

(10)

(11)

根據式(9)，傳統加工模式下的訂單總完工時間為C11+C12=L11+p1+H11+L22+p2+H22。聯立式(10)和(11)，分4種情形證明假設C21+C22

情形1：L12>L22+p22且L21>L11+p11。

在情形1下，分享加工模式對應的目標值C21+C22滿足：

C21+C22=L12+p12+H21+L21+p21+H12>

(L22+p22)+p12+H21+(L11+p11)+p21+

H12=p1+p2+L22+H21+L11+H12>

L11+p1+H11+L22+p2+H22=C11+C12

(12)

式(12)的第1個不等式是依據該情形的條件L12>L22+p22以及L21>L11+p11，第2個不等式是依據假設3推導出的H21>H11與H12>H22。式(12)與假設C21+C22

情形2：L12>L22+p22且L21≤L11+p11。在該情形下，分享加工模式對應的目標值滿足：

C21+C22=L12+p12+H21+L11+p11+p21+

H12>(L22+p22)+p12+H21+L11+p11+

p21+H12=p1+p2+L22+H21+L11+H12>

L11+p1+H11+L22+p2+H22=C11+C12

(13)

式(13)第一個不等式依據該情形的條件L12>L22+p22，第二個不等式依據假設(3)的H21>H11與H12>H22。式(13)與假設C21+C22

情形3：L12≤L22+p22且L21>L11+p11。類似地，結合該情形條件L21>L11+p11以及假設(3)的H21>H11與H12>H22，有

C21+C22=L22+p22+p12+H21+L21+p21+

H12>L22+p22+p12+H21+(L11+p11)+

p21+H12=p1+p2+L22+H21+L11+H12>

L11+p1+H11+L22+p2+H22=C11+C12

(14)

式(14)與假設C21+C22

情形4：L12≤L22+p22且L21≤L11+p11。在該情形下，分享加工模式對應的目標值滿足：

C21+C22=L22+p22+p12+H21+L11+p11+

p21+H12=p1+p2+L22+H21+L11+H12>

L11+p1+H11+L22+p2+H22=C11+C12

(15)

式(15)與假設C21+C22

基于定理2的結論，分析僅分享1個客戶訂單情形下的最優分享策略優于傳統加工模式的充分條件。

定理3：若僅有1個客戶的訂單J1或J2分享加工，則該訂單的最優分享策略優于傳統加工模式的充分條件為

情形1：分享訂單J1，p1>Δ1并且p2

情形2：分享訂單J2，p2>Δ2并且p1

證明：

情形1：客戶1的訂單J1采用分享加工，客戶2的訂單J2完全由制造商2加工。結合L22Δ1。只需證明訂單J1在最優分享策略下的完工時間C21小于傳統加工模式下的完工時間C11。由式(4)可知C11=L11+p1+H11；對于C21，因為訂單J2不拆分加工，式(6)中的p22=p2。討論式(6)中的以下兩種情形：

情形1.1：當L12>L22+p2時，C21=L11+p11+H11=L12+p12+H21Δ1保證了滿足L11+p11+H11=L12+p12+H21的解的存在，即p11=(p1+Δ1)/2，p12=(p1-Δ1)/2。

情形1.2：當L12≤L22+p2時，類似地，C21=L11+p11+H11=L22+p2+p12+H210，結合p11=p1-p12，可推導出p2

綜上，只要p1>Δ1且p2

情形2：客戶2的訂單J2采用分享加工而客戶1的訂單J1完全由制造商1加工。該情形的分析與情形1完全對稱。首先，訂單J1的完工時間始終為C11=C21=L11+p1+H11；其次，由定理1可知分享加工訂單J2要求滿足p2>Δ2；然后，因為訂單J1不拆分加工，式(8)中的p11=p1。基于與情形1類似的分析可以得出，當p2>Δ2且p1

舉例解釋定理3的情形1，如圖4所示。Δ1=(L12+H21)-(L11+H11)=7，訂單J1的加工時間p1=46，訂單J2的加工時間p2=40。

圖4 定理3中情形1的例子Fig.4 Example of case 1 in theorem 3

容易驗證滿足情形1的p1>Δ1且p2

上述3個定理的結論將給予整個制造供應鏈協同調度管理一定的啟示。首先，對于某客戶訂單，只有當訂單的產品需求量相對較大時，距離較遠的制造商才能參與訂單加工，即采用多個制造商分享加工的方案才是有利可圖的；其次，考慮多個客戶訂單時，訂單的分享加工策略與制造網絡中各成員間的距離關系較為復雜。從定理1和3的結論可以看出，只有在訂單大小滿足一定條件時，才能設計合理的訂單拆分方案使其交貨速度快于傳統加工模式。

4 結 語

在分享經濟環境下，制造供應鏈通過共享平臺可以分享不同制造企業的加工資源，提高對客戶需求的響應速度和客戶滿意度。研究由供應商、制造商和客戶組成的供應鏈加工配送網絡，著重考察分享加工模式與傳統加工模式對客戶訂單響應速度的影響。給出了1個供應商、2個制造商與1客戶供應鏈情形下，分享加工模式優于傳統加工模式的條件；對于2個供應商、2個制造商與2個客戶的供應鏈情形，針對制造商采用先到先服務加工規則，指出不能通過同時拆分加工兩個客戶的訂單來改進傳統加工模式的效果，針對只有1個客戶訂單被拆分加工的情形給出了分享加工模式占優的充分條件。本文著重關注供應鏈的響應速度指標，但實際上，制造成本也是一個非常重要的度量指標。因此，后續研究將進一步考慮同時優化供應鏈響應速度和生產成本的分享加工策略設計，此外可將雙客戶的情形拓展至考慮更多客戶的一般情形。