數形從分離走向結合，概念理解從淺顯走向深刻

陳麗

[摘 要]從數與形兩個角度出發，探尋數表征、形表征、數形結合表征概念的教學策略。通過數表征與形表征的相互選擇和轉化，形成概念認知結構，實現學生對概念的深度理解，進一步增強學生的學習力。

[關鍵詞]數學概念;數形結合;正比例

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2022）11-0029-03

數學概念因其抽象的內容和靜態的呈現方式，使得學生學習數學概念較為困難。如何突破該學習難點？筆者嘗試從數學中的兩個基本的研究對象數與形出發，探尋通過數形結合揭示概念本質的教學策略。

一、數學概念學習難點分析

數學概念是對現實對象的數量關系和空間形式的本質特征的一種反映。其表現形式是高度概括、精確的語言，學習難點包括兩個方面。

1.數學概念內容的高度抽象。在小學數學課本中，概念常常是以描述性的文字呈現的。抽象的文字中往往包含著子概念。例如，人教版教材六年級下冊正比例的概念中就包含“相關聯的量”“變量”“比值一定”等概念。對六年級學生而言，要感知動態的、連續的、變化的量，以及理解量變化的背后是比值一定，是比較困難的。

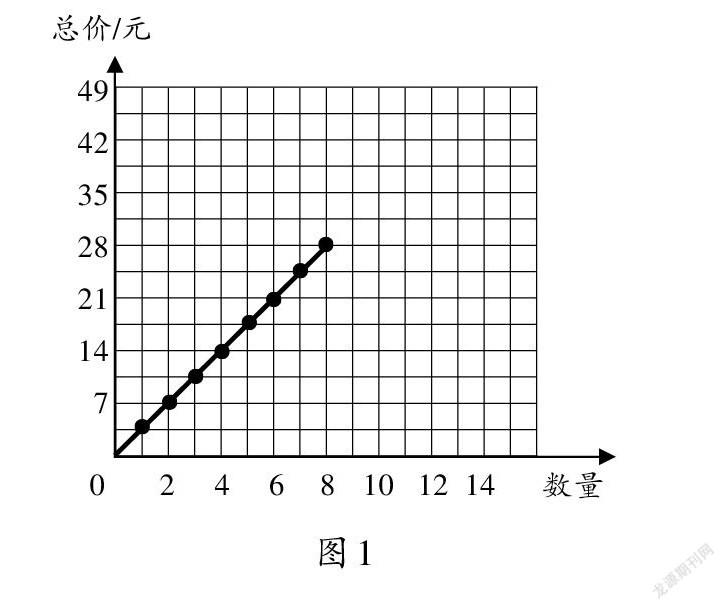
2.數學概念的靜態呈現。抽象的數學概念如果是圖文并茂的，可有助于學生理解。但教材因受篇幅限制，圖示往往較少，即使有也是靜態的。如教材給出了正比例圖像（如圖1）。關于“正比例圖像是如何形成的？它看著很像折線統計圖，有哪些特點？”，學生不得而知。

小學生的思維以直觀形象思維為主，對高度概括、抽象的數學概念理解會比較困難。如何突破難點？“數形結合”不失為一種好方法。

二、數形從分離走向結合的數學概念教學策略

數學研究的兩個基本對象就是數與形。數與形是表述概念的兩種形式，溝通數與形的內在聯系，將數與形結合，有助于深入理解概念。

【策略一】從數的角度出發，表征概念。數表征概念是指通過文字、數與代數式三者之間的相互轉化，進而便于學習者理解概念。

教學片段1：從數據變化的角度初步認識相關聯的量。

思考：下列素材中哪些量在變化？

（1）處于生長發育期的小明的年齡與身高。

（2）一輛汽車行駛的時間和路程。

（3）一本書有100頁，已讀的頁數與未讀的頁數。

（4）用24個邊長為1 cm的小正方形擺長方形。

相關聯的量是正比例概念的上位概念，是學習正比例概念的關鍵。何為相關聯？這對學生來說比較抽象。教學中，教師出示四組材料，讓學生觀察并感受，一個量變化，另一個量也隨之變化，從而清楚地認識兩種相關聯的量，為理解正比例關系做好鋪墊。

教學片段2：數、語言描述與代數式之間的轉化表征正比例概念。

優優買絲帶，買這種絲帶的長度與總價的關系如下表所示：

問題：仔細觀察，表中有哪兩種量？總價是怎樣隨著長度的變化而變化的？總價與相應長度的比是多少？比值是多少？

借助幾個關鍵的問題，讓學生充分經歷量的變化過程，從而發現總價和長度之間的變化規律，同時將目光聚焦到變化中的聯系，即比值不變，也就是單價始終是一定的，并歸納出數量關系式，實現用數、語言描述與代數式之間的轉化來表征正比例概念。

【策略二】從形的角度出發表征概念。形表征概念是指利用實物、圖形、圖像、符號等表征概念，并通過圖形的比較與動態變化達成對概念的理解。

教學片段1：數形對應，動態形成圖像。

問題：

（1）數對（1，3.5）的位置在哪里？你能將表格中的其他數對一一表示出來嗎？把這些點按一定的順序連起來（如圖3），你發現了什么？

（2）這條線段可以向兩端延伸，其中一端延伸到數對（0，0）（如圖4）。數對（0，0）表示什么？

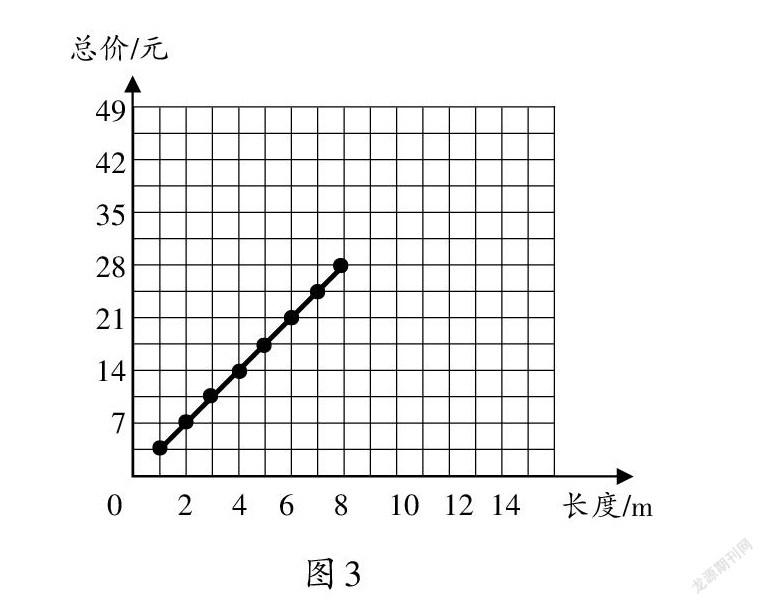
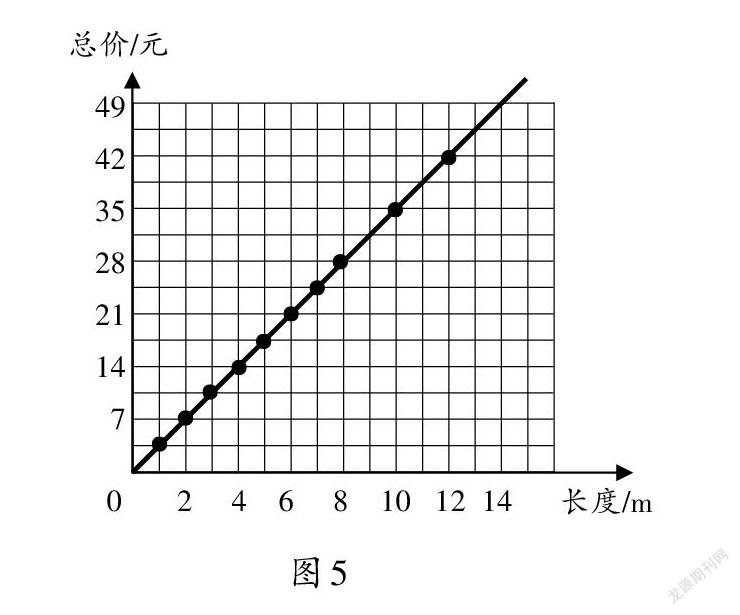
（3）找一找數對（10，35）和（12，42）表示的點，把它們描出來，和前面的點連起來（如圖5），你又能發現什么？

（4）優優買了a m長的絲帶，付了b元，a和b有怎樣的關系？

學生在數表征正比例概念時，已初步感知量的連續變化的特征。通過描點、連線，與原點溝通聯系，結合教師利用多媒體動態的演示，學生發現a和b都是一對一對出現的。隨著直線不斷向上延伸，學生清晰地感受到一種量在擴大的同時， 另一種量也在不斷擴大。學生經歷直觀想象、抽象、建立模型等過程，豐富了正比例概念的表象。

教學片段2：在對比點的位置的過程中厘清對應變量中的不變量。

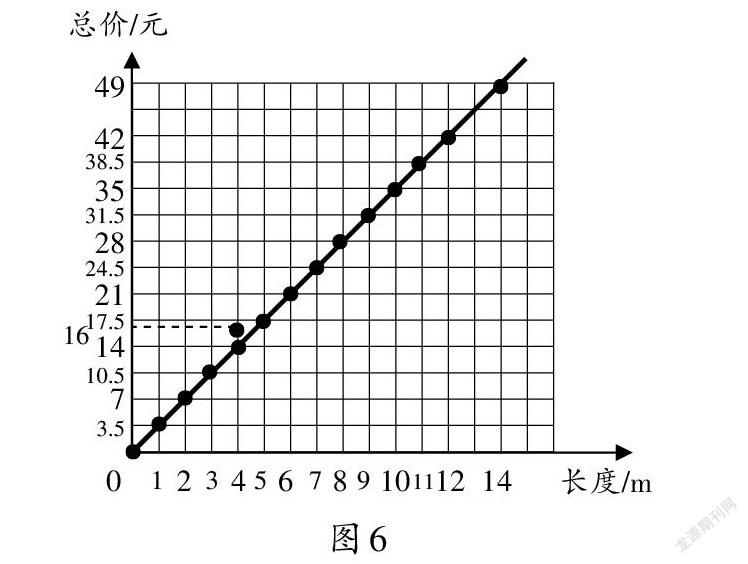
問題：4 m絲帶16元，找一找，（4，16）這個點在剛才那條直線上嗎？11 m絲帶38.5元呢？什么樣的點在這條直線上？什么樣的點不在這條直線上？

學生在圖像動態形成過程中，發現在同一條直線上的這些點，既顯示了絲帶的長度和單價，又反映了長度和單價之間的關系。兩種變量之間的關系是正比例概念教學的難點之一。教學中，筆者增加了根據2組數據描點的環節，其中，一個點在這條直線上，另一個點不在這條直線上（如圖6）。通過正例與反例的對比，幫助學生厘清兩個變量之間的關系——背后的不變量，形成正比例圖像，初步感受函數思想。

【策略三】數表征與形表征互相轉化，形成綜合圖式表征概念。

教學片段1：在形表征中找數。

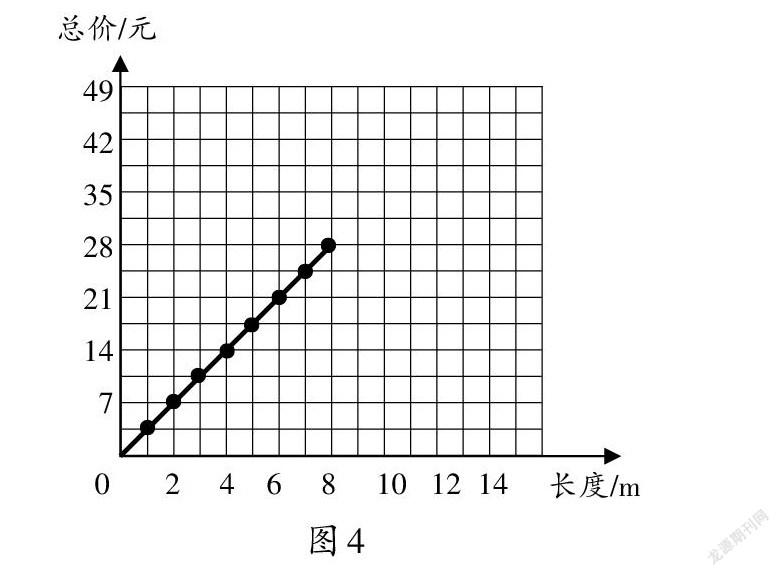
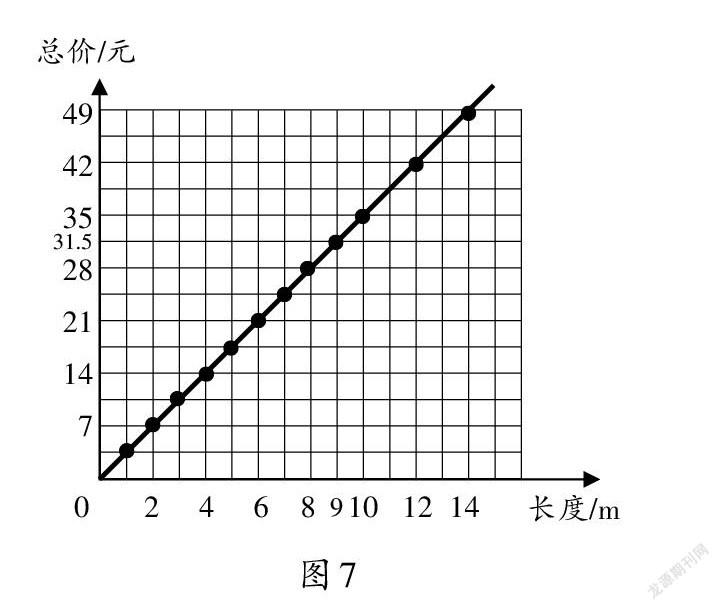
問題：如果買9 m的絲帶，你能根據圖像判斷總價是多少嗎？49元又能買多長的絲帶？（答案見圖7）

正比例圖像的形成并不意味著教學的結束。教學中，讓學生依據圖像，由一個量的值推斷、估計另一個量的值，由一種量之間的關系推斷另一種量之間的關系。學生可以根據圖像的特點進行推理，將形轉化為數，體會函數的形表征和數表征之間的聯系。

教學片段2：在數表征中思形。

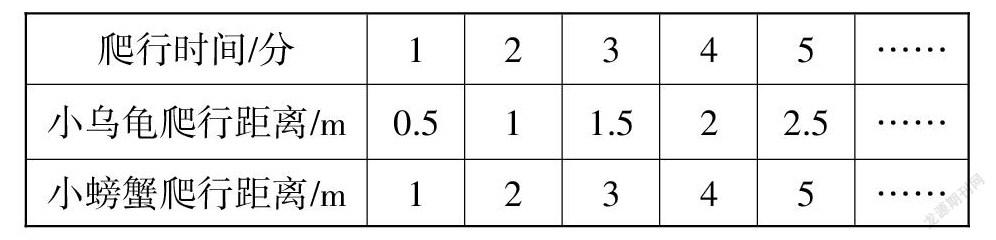
小烏龜和小螃蟹比賽，爬行時間和爬行距離如下表所示：

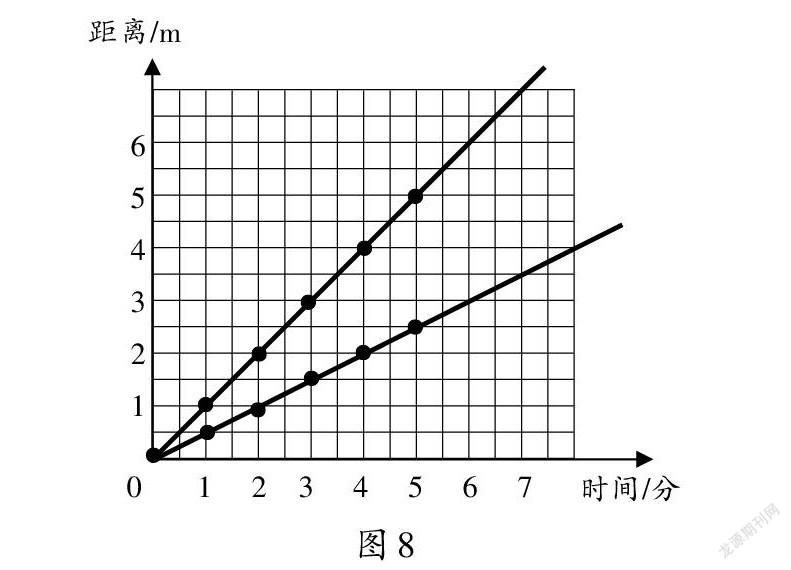
問題：想一想，小烏龜和小螃蟹的爬行時間和爬行距離成正比例關系嗎？

觀察小烏龜和小螃蟹的爬行情況圖像（如圖8），想一想，圖像中的兩條直線分別代表哪一種小動物的爬行情況？后來小海龜也參加了比賽，他的爬行速度比小螃蟹還要快一些，你覺得他的爬行情況圖像可能是怎樣的？

這里借助兩種動物爬行時間與距離的數據，在同一幅圖中，用圖像表征速度快慢的樣子，以數思形;通過數形、形形對比，感悟數與形的對應關系，以數解形，深刻體會正比例概念的本質。

【策略四】在概念溝通中，形成概念綜合圖示。

概念綜合圖示的形成，需要將概念的形成過程與結果進行溝通，將概念的各種表征形式進行溝通，將已學的概念與后續延展的內容進行溝通。

（1）在回顧中溝通。從具體的實例出發，回顧經歷數據的分析、比較與抽象，圖像的動態形成以及特征等研究過程，溝通正比例概念的文字表征、代數式表征和圖像表征之間的聯系，形成正比例圖像。

（2）在延伸中溝通。從縱向出發，與后續研究內容進行溝通。初中學習的正比例圖像，是一條過坐標原點的直線。通過延伸，溝通了正比例概念文字與圖像的聯系。

（3）在比較中溝通。從橫向出發，將相關聯的概念進行溝通。在學習正比例概念之后，教師順勢引導：“正比例和反比例之間有什么區別與聯系？你能從四組材料中找出成反比例關系的那一組嗎？”為學生形成函數概念圖示做好準備。

在概念的教學中，挖掘概念中的“數”是什么、“形”是什么，采用以形助數或以數解形的方法，從數表征、形表征、數形結合表征概念入手理解概念。在數表征概念中，力求提供豐富的實例，在分類與比較中形成概念表象。在形表征概念中，借助現代教育技術等展示形的動態變化，力求通過觀察、操作、想象形成概念之形表象。在數形結合表征概念時，力求讓數表征與形表征互相轉化。由數思形，由形譯數，使學生經歷數與形的對應、數與形的轉化過程，形成綜合概念圖示，以達到對概念深度理解的程度。

（責編 吳美玲）