幾何直觀，數學思維的“助推劑”

呂夢嬋

【摘? 要】幾何直觀作為新課標提出的小學數學核心素養之一，貫穿四大數學學習領域，其重要地位是毋庸置疑的。在新課改的理念引領下，教師在課堂教學中應該注重潛移默化地滲透幾何直觀思想，培養學生的幾何直觀能力，在寓學于趣中實現數學思維進階，進而提升學生的數學核心素養。

【關鍵詞】小學數學;幾何直觀;數學思維

本文以筆者執教的小學數學五年級基于幾何直觀的教學片段為例，對幾何直觀數學思維進行探討，為一線教師提供參考，為自己今后的幾何直觀教學指明方向，進一步拓寬學生的思維廣度，在直觀體驗中提升學生的綜合能力與素養。

一、潛移默化，滲透幾何直觀思想

（一）幾何直觀的內涵

何為幾何直觀？數學課程標準中的解釋：幾何直觀主要指利用圖形描述和分析問題，借助幾何手段把復雜的數學問題變得簡明、形象，有助于探索解決問題的思路。國內外學者對幾何直觀的概念界定各不相同，大致分為兩種：一種觀點認為它是側重于“直觀”的方法手段，另一種則更傾向于把它定義為能力素養。二者雖不同，但彼此又有相通之處，從數學教育的角度，參照數學課程標準中對幾何直觀的說明，基本可以歸結為利用實物、圖形等直觀語言描述和分析問題，對研究的數學對象進行直觀感知和整體把握。

（二）小學生運用幾何直觀的現狀

在當前家長和社會都高度關注學生考試成績的背景下，許多教師的教學方法會或多或少地受到這種風潮的影響，再加上一些教師自身素養的局限，導致課堂教學流于表面，一味地灌輸知識點，不斷地瘋狂刷題，試圖讓學生通過“死記硬背”和“題海戰術”來提高分數，在這種形勢下的幾何直觀教學是欠缺的，是不受重視的。

大部分數學教師對教材和課標的把握還是準確到位的，他們在課堂教學過程中或多或少地都會滲透幾何直觀的思想，教授通過直觀圖形來輔助解題的具體方法。從筆者的課堂教學和作業反饋中不難發現一個問題，少部分學生見到稍復雜的題目都懶得畫圖來幫助解題，他們寧愿盯著題目看半天也不愿意動手操作，實在想不出來了就隨意寫幾道算式。

細思原因，我歸結為以下三點：第一，這類孩子大都習慣于上課走神開小差，老師介紹方法時根本沒聽;第二，思想上不重視畫圖助解的方法，覺得把算式寫出來才能得分;第三，寫作業只圖速度快，敷衍了事。小學數學作為整個數學教育的起始，是夯實基礎的重要時期，對以后的數學學習有深遠的影響，如果學生在這一階段敷衍應付，忽視了幾何直觀的重要性，那必將對今后的理科學習產生不利影響。

（三）滲透幾何直觀思想的必要性

當今社會信息網絡技術發達，知識的獲取變得輕而易舉，學生的知識儲備也非常豐富，因此，學校教育的重點不應局限于學生知識獲取的多少，而應該關注學生的知識是怎么得來的，關注學生學習的過程，更應該助力學生的思維發展。

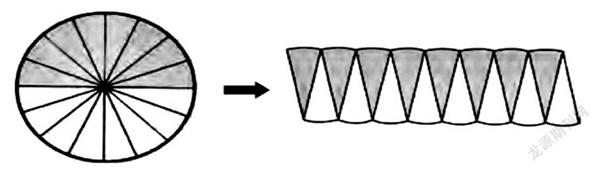
例如，在教學“圓的面積”時，教師應善用教材，帶領學生探索實踐，豐富學生的幾何直觀意識，在動手操作中逐步推導出圓的面積公式。在動手操作之前，教師應明確活動要求：把一個圓剪下來，按16等份剪開，再按照書上的示范拼一拼，看看你能得到一個什么樣的圖形。在交流討論之后，大家達成共識：拼成了一個近似的平行四邊形。此時教師應提問：“這個平行四邊形的面積和圓的面積相等嗎？”緊接著追問：“那我們先求出這個平行四邊形的面積，需要哪些數據？這些數據都是已知的嗎？”學生立刻就能從圖形中看出平行四邊形的高是未知的。在此處教師應順勢激發學生繼續轉化的需求，接著把圓平均分成32份，學生在操作觀察之后不難發現這個圖形更接近長方形了，教師借機提問：“如果繼續把圓平均分成64份、128份、256份……拼成的圖形會怎么樣呢？”學生借助圖形直觀加以聯想就能得出：平均分的份數越多，拼成的圖形越接近長方形。

轉化之后，長方形的長和寬的推導更需要借助幾何直觀來觀察發現，大多數學生能夠通過圖形直觀地發現：長方形的寬是圓的半徑r，長方形的長是圓周長的一半πr。少部分學生仍然沒明白，這時就需要教師借助實物直觀來幫助學生理解，把一個可以平均分成多個扇形的圓形磁性教具粘在黑板上，一步步展示拼成長方形的過程，最后通過求長方形的面積推導出圓的面積。圖形直觀加上實物直觀，這兩種幾何直觀的方法相輔相成，使學生更透徹地掌握了圓的面積公式是怎么得出的，也更清楚地掌握了數學知識的本質，利用幾何直觀達到知其然也知其所以然的效果。

學生通過轉化圖形的實踐操作，在教師的逐步引導下，依托幾何直觀來分析推理，更深層次地掌握了圓的面積的算法和由來，進而可以把這種思維方式遷移到其他的數學問題中去。教師在以教材為基礎的教學過程中滲透幾何直觀思想，不僅豐富了學生的數學知識框架體系，提高了學生對數學知識的應用能力，還發展了學生的邏輯思維能力。

二、探索實踐，鍛煉幾何直觀能力

心理學視角下，幾何直觀是一種思維形式，幾何直觀能力則被認為是一種數學思維能力，是將數學對象運用幾何語言進行表達的能力。幾何直觀能力可以直接幫助學生表征問題從而推動問題的解決，幾何直觀能力的發展也是其他學習能力發展的“橋梁”，更是助推數學思維發展的“跳板”。

直觀能力是否與生俱來還有待商榷，但值得肯定的是，但凡能力都是可以通過后天的學習培養出來的。教師不僅要在新知教學中滲透幾何直觀思想，還要在后續的鞏固練習中實現學生幾何直觀能力的有效鍛煉，進而提高學生應用幾何直觀解決問題的能力。

（一）運用多媒體激發幾何直觀的應用興趣

如今信息技術高度發達，在各行各業中的應用都十分廣泛，教師也應該通過學習來提高自己運用信息技術的水平，從而將信息技術應用到日常教學活動中，提升課堂教學的效果。PPT、幾何畫板、圖形計算器等多媒體技術都是教師需要努力精進的，生動的課件展示能夠迎合小學生的年齡特點，迅速吸引學生的注意力，激發學生對運用圖形助解的興趣。教師應從學生的喜好出發，激起學生主動應用幾何直觀的意識，為學生主動應用和知識內化打下基礎。

（二）巧妙設計環節體會幾何直觀的應用價值

很多學生的幾何直觀應用意識非常薄弱，遇到難以解決的問題寧愿選擇逃避也不愿意畫圖分析，一個重要的原因是他們從思想上根本沒有意識到幾何直觀的價值，沒有感受過應用幾何直觀帶來的便捷。所以教師應該思考如何巧妙設計教學過程，讓學生從方法的運用中嘗到甜頭，這樣學生才會選擇慢慢接受和嘗試。比如教師可以設計一個需要運用幾何直觀來解決的環節，先讓學生自主嘗試各自不同的解法，思考未果之后教師適時出示相關的圖式，先運用正向思維從圖中找數學信息，說說與原題的異同，接著用逆向思維整理原題中的信息，形成對應的圖式來完善自己的思路。一正一逆思維的訓練會讓學生形成對比印象，更加深刻具體地感受幾何直觀的應用價值。

（三）豐富應用領域創造幾何直觀應用時機

筆者教學分數內容時遇到這樣的題目：“把3個橙子平均分成4份，每份是1個橙子的幾分之幾？”這個題目學生解答時幾乎是全軍覆沒，很多同學都思維定式先看問題沒有單位，就直接想成：把3個橙子看作單位“1”，把單位“1”平均分成4份，每份就是。可是這道題的關鍵在于第二小句問題的單位“1”變了，不再是3個橙子，而是1個橙子。我理清了這道題的易錯點后，便向理解了的同學繼續講解：“1個橙子的幾分之幾就是問我們每份有多少個橙子，就是用3個橙子除以4得個橙子，也就是1個橙子的。”話音落下，很多同學都流露出似懂非懂的表情，我借機說道：“回憶一下我們是如何探究分數與除法的關系的？能不能嘗試畫圖來解決這個問題呢？”立即有同學搶答道：“哦，畫那個圓餅圖。”學生各自畫完后，請學生投影展示：“把3個橙子一個一個地分，把每個橙子畫作一個圓，每個橙子都平均分成4份，都取其中的一份涂上陰影，把這三小塊涂陰影的放到一個橙子里，就可以得出就是1個橙子的。”此時大家紛紛點頭，從學生的表情就可以看出他們借助圖形之后立刻就弄明白了。一些復雜抽象的數學知識對小學生來說確實晦澀難懂，這就需要教師的適時點撥，引入幾何直觀來打開學生的思維，打破數學知識領域之間的隔膜，促進學生對數學知識的融會貫通。

（四）設置專門課程訓練幾何直觀應用方法

數學學科的知識點較多，很多作業難題也都需要教師利用課堂時間講解，然而數學課堂上的時間十分寶貴，因此，許多教師只能一味地抓緊時間上課講練習，即使遇到需要幾何直觀來解決的問題，也大都是就題講題，缺乏拓展延伸與系統講解。教師應該意識到，“質”比“量”更重要，教師更需要優化課程設計而非泛泛而講，挑重點講難點可以節約許多課堂時間，這樣教師就可以利用抽離出來的時間對一些重點內容進行單獨訓練。學生幾何直觀能力的養成并不是一蹴而就的，需要教師重視起來并長期進行規范訓練，利用整節課或是在常規課中設計一個環節來專門教學幾何直觀的方法與技巧，進而真正提升學生靈活運用幾何直觀來解決問題的能力。

三、經驗內化，發展提升數學思維

幾何直觀方法與技巧需要在教師的引導下不斷地訓練，在此過程中學生在原有的知識基礎上逐漸建構生成，把習得的經驗揣摩內化，完善自己的知識體系。在學生借助實物或圖形進行思考和推理的過程中，數形結合帶來的直觀感受豐富了形象思維，幫助學生從冗雜的問題情境中剝離出數學本質，讓學生聚焦于思維碰撞過程。

“把握數學本質，優化思維表達”是幾何直觀教育價值的體現，靈活運用幾何直觀表征數學問題，學生能更好地體會幾何直觀在數學知識建構中的作用，進而拓寬思維路徑，鍛煉探索實踐能力。隨學段螺旋上升的幾何直觀能力會讓學生思維產生進階，學生的幾何直觀能力也會隨著思維水平的提高而得到進一步發展，在二者的相互促進下，形成一個良性循環，助推彼此的發展，提高學生分析和解決問題的綜合能力，進而提升學生的數學核心素養。

【參考文獻】

[1]中華人民共和國教育部.義務教育數學課程標準（2011年版）[S].北京：北京師范大學出版社，2012：5.

[2]錢珮玲.幾何課程教學設計應注意的問題[J].數學通報，2009，48（5）：11.

[3]劉愛東.凸顯幾何直觀的教學價值[J].教學與管理，2013（8）：38.