歐拉定理的Python簡單驗證
王德貴
在數論中,歐拉定理(Euler Theorem),也稱費馬-歐拉定理或歐拉函數定理,是一個關于同余性質的定理,它也是數論四大定理(威爾遜定理、費馬小定理、孫子定理、歐拉定理)之一。

數學史上公認的4名最偉大的數學家分別是:阿基米德、牛頓、歐拉和高斯。阿基米德有“撬起地球”的豪言壯語,牛頓因為蘋果聞名世界,高斯少年時就顯露出計算天賦,唯獨歐拉沒有戲劇性的故事卻讓人印象深刻。
然而,幾乎每一個數學領域都可以看到歐拉的名字——初等幾何的歐拉線、多面體的歐拉定理、立體解析幾何的歐拉變換公式、數論的歐拉函數、變分法的歐拉方程、復變函數的歐拉公式……歐拉還是數學史上最多產的數學家,他一生寫下886本書籍論文,平均每年寫出800多頁,彼得堡科學院為了整理他的著作,足足忙碌了47年。他的著作《無窮小分析引論》《微分學》《積分學》是18世紀歐洲標準的微積分教科書。歐拉還創(chuàng)造了一批數學符號,如f(x)、Σ、i、e等等,使得數學更容易表述、推廣,歐拉是18世紀數學界最杰出的人物之一。并且歐拉把整個數學推至物理的領域,此外還涉及建筑學、彈道學、航海學等領域。
對正整數x,歐拉函數是小于x的正整數中與x互質的數的數目。求法通式為(圖1):

x (1 - 1/p1)* … * (1 - 1/pn)。其中p1, p2……pn為x的所有質因數,x是不為0的整數。φ(1)=1[唯一和1互質的數(小于等于1)就是1本身]。
注意:每種質因數只算一個。 比如12=2*2*3那么φ(12)=12(1-1/2)(1-1/3)=4。
還可以根據定義求解,即統計小于x的所有值中與x互素的個數。當x為素數時,φ(x) = x -1。

其中為歐拉函數,gcd(a,m)求兩數最大公約數,如果為1則互素。
特別是當m為素數時,該結論即為費馬小定理,因為也稱歐拉定理是費馬小定理的推廣。
基本思路就是根先輸入n和a,并判斷是否互素,然后用定義法和通式法求出歐拉函數值,計算冪,求模后判斷,如果為1,則歐拉定理成立。
程序設計涉及到的是等級考試四級或二級內容。
1.輸入n和a,并判斷是否互素(圖3)

2.求歐拉函數值(圖4)

3.計算冪,并求模(圖5)

4.判斷模的值,如果為1,則輸出歐拉定理成立(圖6)

5.完整程序
為了能循環(huán)驗證,將所有程序加在循環(huán)里面(圖7);

如果輸入12和8,則提示非互素,程序返回;輸入12和5,輸出歐拉定理成立;當輸入11和5時,皆為互素,其實就是費馬小定理的驗證,這里不做贅述,有興趣的朋友可以參考筆者之前發(fā)的文章(圖8)。

其實上述這個程序所涉及的知識點是等級考試二級內容。
6.利用自定義函數
這是等級考試四級內容。
從上述程序里,大家看到,判斷互素用了兩次,所以使用自定義函數應該是更好一些,思路比較清晰(圖9)。
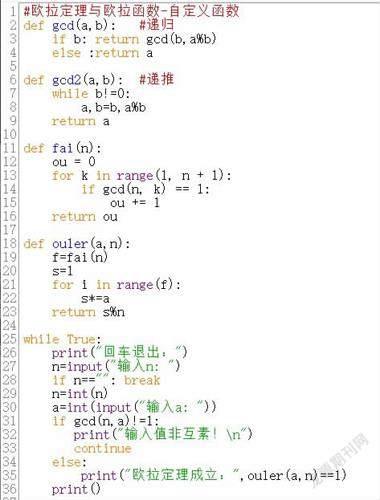
這里定義了兩個求最大公約數的函數,以此來判斷是否互素,一個是遞歸函數,一個是遞推函數,放在一起,便于比較理解。fai()函數是求歐拉函數值,ouler()調用fai()函數求得f值,然后計算a的f次冪,并對n求模。
主程序中判斷ouler()函數返回值,如果為1,則說明歐拉定理成立。
前面我們利用歐拉定理的定義來驗證其正確性,而在歐拉函數求法時,前面用的是定義形式,這里還可以用通用式來求歐拉函數值(圖10)。

這是自定義函數求歐拉函數值,測試結果與之前相同。大家也可以研究其他編程方法,這里不再討論。
本文如有不當之處,請各位同仁、朋友斧正。

