金屬波紋管剛度的簡化有限元分析*

劉達列 胡瀟毅

(浙江農(nóng)林大學(xué)光機電工程學(xué)院 浙江杭州 311300)

金屬波紋管具有位移補償、連接、密封、減震等重要作用，作為基礎(chǔ)元件在機械密封系統(tǒng)、管道系統(tǒng)、冷卻系統(tǒng)、船舶和電力等領(lǐng)域廣泛應(yīng)用[1]。金屬波紋管的力學(xué)性能對整個系統(tǒng)的安全運行具有重要意義，研究人員對金屬波紋管的剛度、強度、穩(wěn)定性、疲勞壽命及振動特性等做了大量研究[2-10]。尤其是剛度作為波紋管設(shè)計的主要性能參數(shù)，是波紋管力學(xué)性能研究的熱點。有限元分析技術(shù)在剛度特性研究中的應(yīng)用非常普遍。姜宏春等[2]利用ANSYS對擠壓成型波紋管的軸向剛度進行了計算，并與EJMA經(jīng)驗公式計算結(jié)果進行了對比。萬宏強和汪亮[3]通過對計算經(jīng)驗公式的溫度修正，應(yīng)用有限元軟件計算了低溫環(huán)境下的波紋管軸向剛度。占豐朝等[4]采用有限元方法對不等壁厚的U形波紋管剛度進行了非線性分析，并通過實驗結(jié)果進行了驗證。譚金等人[5]利用有限元研究了波紋管波片波形直線段、圓弧段幾何尺寸對其剛度的影響。修筑等人[6]對工業(yè)上常用波紋管的軸向剛度進行了仿真計算，分析了壁厚變化對軸向剛度的影響，并與實測數(shù)據(jù)進行了對比。在這些研究中，主要采用實體殼單元或者軸對稱單元來模擬波紋管，但由于波紋管特殊的幾何形狀，通常需要生成大量單元來進行分析。尤其當(dāng)波紋管僅僅是大型模型的一部分，而需要對整個模型進行分析，或者需要研究波紋管參數(shù)對整個系統(tǒng)的影響時，采用實體殼單元等建模較為耗時，效率較低。

本文作者利用ANSYS軟件的Matrix27剛度單元建立波紋管簡化模型，對不同試件的軸向剛度和扭轉(zhuǎn)剛度進行有限元計算，并與實體有限元模型計算結(jié)果及EJMA工程實際經(jīng)驗公式計算值進行了對比，從而驗證該簡化模型的可靠性。同時應(yīng)用該簡化模型對含有波紋管的整體系統(tǒng)的結(jié)構(gòu)分析進行了研究。

1 Matrix27剛度單元模型理論

對于金屬波紋管，尤其是作為位移補償件的波紋管來說，在使用過程中的剛度屬性是它最主要的特性。按照不同的載荷及位移性質(zhì)，波紋管剛度又可分為軸向剛度、彎曲剛度、扭轉(zhuǎn)剛度等。文中利用ANSYS軟件[11]的Matrix27剛度單元來模擬波紋管的剛度特性，同時滿足結(jié)構(gòu)靜態(tài)平衡的要求。該單元無需定義波紋管本身的幾何尺寸，只由矩陣中的各個系數(shù)來反映單元總體的彈性運動響應(yīng)特性。假設(shè)波紋管兩端的變形較小，滿足經(jīng)典梁理論的平面截面條件，則波紋管兩端的變形模式完全可以由兩端橫截面中心處的3個平移和3個轉(zhuǎn)動分量確定。Matrix27剛度單元是通過2個節(jié)點構(gòu)成的一種有限元單元，每個節(jié)點具有6個自由度，即3個線位移和3個角位移。該單元由12×12剛度矩陣K表示，即

該矩陣為對稱矩陣，共有78個獨立的系數(shù)，即k1，k2，…，k78，這些系數(shù)與波紋管的剛度屬性直接相關(guān)。計算出矩陣中的78個獨立系數(shù)，即可在ANSYS中定義Matrix27單元的78個實常數(shù)，從而創(chuàng)建波紋管簡化模型。由Matrix27單元的剛度矩陣屬性可得[12]

(1)

其中K11的含義為：當(dāng)Matrix27單元2個節(jié)點中其中一個節(jié)點i固定時，只需要考慮另一個節(jié)點j的6個自由度，即矩陣K可簡化為一個6×6的剛度矩陣來描述節(jié)點j處的力和變形之間的關(guān)系:

(2)

其中kxx為X方向或軸向的線剛度；kyy、kzz為Y方向和Z方向的線剛度；kφφ為繞X軸的轉(zhuǎn)動剛度即扭轉(zhuǎn)剛度；kθθy和kθθz為繞Y軸和Z軸轉(zhuǎn)動剛度；kθy、kθz為節(jié)點處彎矩與沿Y軸、Z軸的線位移之間的彎曲剛度。剛度矩陣K可用于描述不同形式的波紋管如矩形和U形波紋管的剛度屬性。文中主要研究U形波紋管。對于U形波紋管，由于周向?qū)ΨQ性，可得kyy=kzz，kθθy=kθθz=kθθ和kθy=kθz。

同理，K22描述另一個節(jié)點j固定時，節(jié)點i處的力和變形之間的關(guān)系。由于波紋管結(jié)構(gòu)的對稱性，可知

K22=K11

K矩陣中的另外2個分矩陣為

K12=DK22

及

其中D為平衡轉(zhuǎn)換矩陣：

(3)

式中：Lb為波紋管總長度。

綜上可得，要想在ANSYS中創(chuàng)建Matrix27剛度單元來準確模擬波紋管，必須先通過理論計算或者實驗測試確定各剛度值，其中采用EJMA標準提供的工程近似法是一種較為簡便的剛度計算方法[13]。EJMA給出U形波紋管軸向剛度的經(jīng)驗計算公式為

(4)

式中：Dm為波紋管平均直徑；t為波紋管壁厚；n為波紋管的波數(shù)；w為波高；Eb為波紋管材料在室溫下的彈性模量；Cf為系數(shù)，也可由EJMA標準查到。

Y方向和Z方向的線剛度為

(5)

式中：L為波紋管總長度。

U形波紋管繞X軸的轉(zhuǎn)動剛度即扭轉(zhuǎn)剛度的計算公式為

(6)

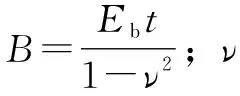
繞Y軸和Z軸的轉(zhuǎn)動剛度為

(7)

節(jié)點處彎矩引起Y軸和Z軸線位移的彎曲剛度為

(8)

通過以上各式計算波紋管的剛度分量并代入剛度矩陣K，即可在ANSYS中創(chuàng)建基于Matrix27剛度單元的簡化模型來模擬波紋管。以上公式主要針對U形波紋管給出，如對矩陣K里面的剛度系數(shù)略作調(diào)整，也可模擬其他形式的波紋管，如矩形波紋管等。

2 波紋管有限元建模

文中采用U形波紋管作為算例，分別建立有限元實體模型和簡化模型，計算2種不同有限元模型得到的軸向剛度和扭轉(zhuǎn)剛度，并將簡化模型的分析結(jié)果與實體有限元模型結(jié)果以及EJMA理論值進行比較。U形金屬波紋管的幾何結(jié)構(gòu)如圖1所示，do為波紋管外徑，di為內(nèi)徑，q為波距，rh為波峰中線半徑，rv為波谷中線半徑。

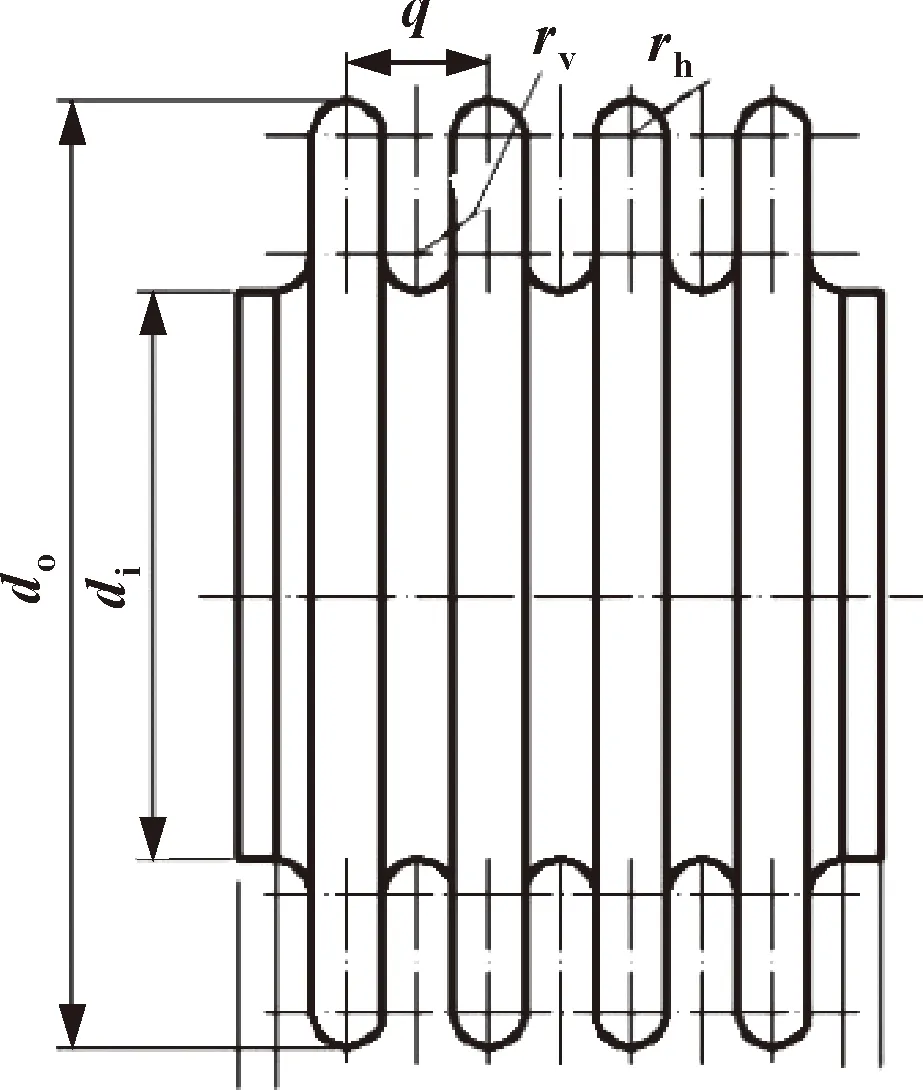
圖1 波紋管結(jié)構(gòu)參數(shù)Fig.1 Structural parameters of bellows

下面共選用4個試件進行分析，其中試件1和2取自于文獻[14-15]的實驗?zāi)Ｐ停嚰?和4取自于某密封系統(tǒng)的連接波紋管實物模型。試件的結(jié)構(gòu)尺寸如表1所示。波紋管材料的彈性模量E=207 GPa，密度ρ=7 850 kg/m3，泊松比ν=0.3。

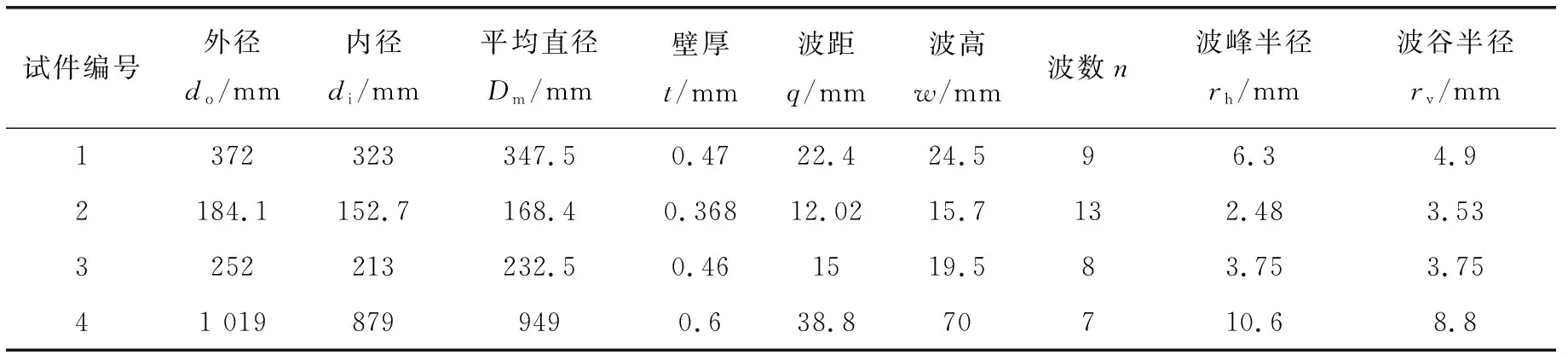
表1 波紋管結(jié)構(gòu)尺寸Table 1 Structural parameters of bellows samples

2.1 波紋管實體模型建模

首先基于有限元軟件ANSYS建立波紋管實體模型，選擇殼體單元shell63[11]進行模擬。由于波紋管屬于薄壁結(jié)構(gòu)，殼體單元shell63具有彎曲能力和薄膜效應(yīng)，能承受面內(nèi)載荷和法向載荷，同時具有分析塑性、應(yīng)力硬化、大變形、大應(yīng)力的能力，能較好地模擬波紋管結(jié)構(gòu)。建立的有限元模型如圖2所示，網(wǎng)格劃分時在波紋管圓弧段及一些圓弧過渡處進行了網(wǎng)格細化處理。為分析波紋管的剛度屬性，此處采用一端固定，另一端自由的約束條件來模擬波紋管的工作狀態(tài)。

圖2 波紋管有限元實體模型Fig.2 Solid FEA model of bellows

2.2 波紋管簡化模型建模

再對4個波紋管試樣利用Matrix27剛度單元建立有限元簡化模型。首先根據(jù)波紋管結(jié)構(gòu)參數(shù)計算剛度矩陣K的各個系數(shù)，用于定義Matrix27單元的78個實常數(shù)。然后在波紋管兩端中心處創(chuàng)建2個節(jié)點，連接2個節(jié)點并生成Matrix27單元就完成了簡化模型的建模。另外在兩端中心節(jié)點處各生成一個質(zhì)量單元Mass21來模擬波紋管本身的質(zhì)量，即每個質(zhì)量單元表示1/2的波紋管總質(zhì)量。建立的有限元模型如圖3所示，可以看到該模型非常簡單。在模型兩端節(jié)點施加與實體模型同樣的載荷和約束條件即可計算其剛度結(jié)果，并與實體模型計算結(jié)果進行比較。

圖3 波紋管簡化有限元模型Fig.3 Simplified FEA model of bellows

3 波紋管剛度計算結(jié)果及分析

完成有限元建模后即可對波紋管的軸向剛度和扭轉(zhuǎn)剛度進行計算。在自由端施加軸向載荷后可求得波紋管的軸向剛度為

kx=Fx/x

(9)

式中：Fx為軸向力；x為Fx作用下的軸向位移。

在彈性范圍內(nèi)，通過有限元模型求出波紋管受不同載荷后產(chǎn)生的軸向位移，將軸向位移x和軸向作用力Fx代入式(9)，即可求得波紋管的軸向剛度。

同樣對有限元模型施加扭轉(zhuǎn)載荷后即可求得波紋管的扭轉(zhuǎn)剛度為

kφ=T/φ

(10)

式中：T為自由端施加的扭矩；φ為扭矩作用下的扭轉(zhuǎn)角。

基于上述2種有限元模型計算的軸向剛度值、扭轉(zhuǎn)剛度值與EJMA經(jīng)驗公式(4)、(6)的計算結(jié)果的對比如表2所示。可以看出，簡化模型與EJMA經(jīng)驗公式的計算結(jié)果非常接近，其誤差在1%以內(nèi)。而實體模型所得結(jié)果與EJMA經(jīng)驗公式的計算結(jié)果的誤差也基本在5%以內(nèi)，與簡化模型的軸向剛度和扭轉(zhuǎn)剛度結(jié)果也基本一致。同時將文中試件1和試件2的簡化模型計算結(jié)果與文獻[14-15]中的有限元計算結(jié)果及實驗測試值進行對比，如表3所示，其結(jié)果也同樣保持一致。由簡化模型的剛度計算結(jié)果與EJMA理論計算值、實體有限元模型計算結(jié)果以及實驗測試結(jié)果的全面比較，說明文中采用的波紋管有限元簡化模型準確可靠。因文獻[14-15]并未進行波紋管扭轉(zhuǎn)剛度測量，表3中僅給出軸向剛度實驗測量結(jié)果。

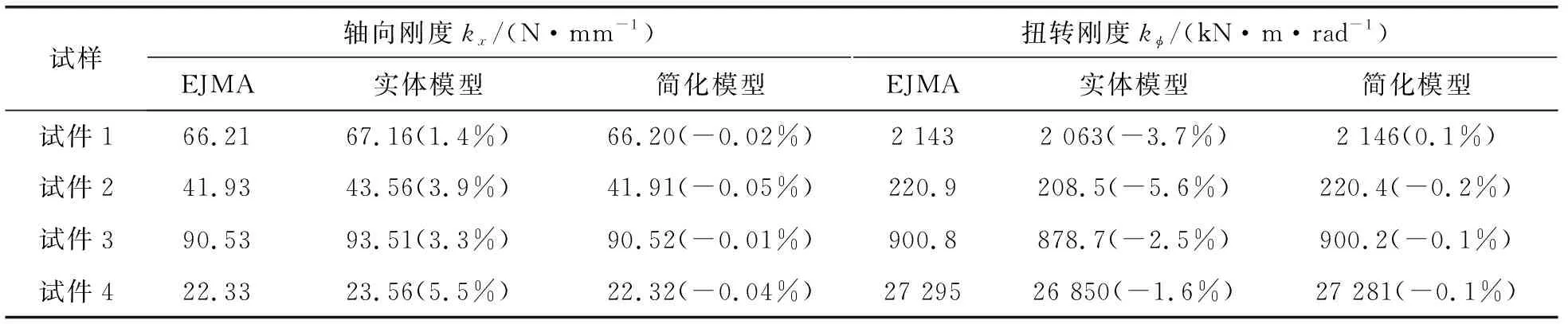
表2 波紋管剛度值比較Table 2 Comparison of bellows stiffness results

表3 波紋管有限元計算結(jié)果與部分實驗值[14-15]Table 3 FEA calculating results and part experimental values of bellows

從剛度矩陣K的推導(dǎo)過程可知，Matrix27剛度單元的實常數(shù)的物理意義就是波紋管的剛度屬性，而建模時實常數(shù)就是直接由EJMA理論值給出的，因此簡化模型的剛度計算結(jié)果與EJMA理論值完全吻合是符合預(yù)期的。同時也說明在建模時可以對Matrix27單元的剛度矩陣系數(shù)進行靈活的調(diào)整，如在波紋管介質(zhì)壓力、溫度等工作狀態(tài)發(fā)生變化時，可以根據(jù)實際情況改變剛度矩陣系數(shù)。因此該簡化模型相比較于其他模型更容易進行修正。此外，也可以根據(jù)其他形式的波紋管比如矩形波紋管的剛度計算公式來建立剛度矩陣，從而創(chuàng)建適用于矩形波紋管的簡化模型，讓文中方法具有更廣泛的應(yīng)用場景。

此外，當(dāng)波紋管僅僅是大型模型的一部分，而需要對整個模型進行結(jié)構(gòu)分析，或者需要研究波紋管參數(shù)對整個系統(tǒng)的影響時，采用實體殼單元等進行波紋管建模較為耗時，效率較低。而基于Matrix27剛度單元創(chuàng)建波紋管簡化模型則非常簡便。文中也對波紋管作為整體模型一部分時的情況進行了進一步分析，例如使用波紋管連接2個大型金屬密封箱體的場景。圖4中給出了采用殼單元和Matrix27單元模擬波紋管來連接金屬密封箱體的有限元整體模型和網(wǎng)格模型。對整體模型施加相同的載荷和邊界條件，得到的應(yīng)力和位移結(jié)果如圖5所示。可見，采用2種波紋管模型的整體結(jié)構(gòu)應(yīng)力和變形分布都保持了一致，其最大等效應(yīng)力均為72.3 MPa，最大總位移均為13.2 mm。雖然該結(jié)構(gòu)整體并不復(fù)雜，但是從中可以發(fā)現(xiàn)基于簡化波紋管模型進行整體建模的效率更高，在研究波紋管參數(shù)對整體系統(tǒng)的影響時也更為簡便，并能應(yīng)用于矩形波紋管和U形波紋管等不同結(jié)構(gòu)，對基于整體系統(tǒng)響應(yīng)的各類波紋管結(jié)構(gòu)參數(shù)優(yōu)化等研究具有通用意義。

圖4 整體模型中的波紋管建模Fig.4 Modeling of bellows as a part of the whole system:(a)shell elements model of bellows in the system;(b)Matrix27model of bellows in the system;(c)shell elements model meshes;(d)Matrix27 element model meshes

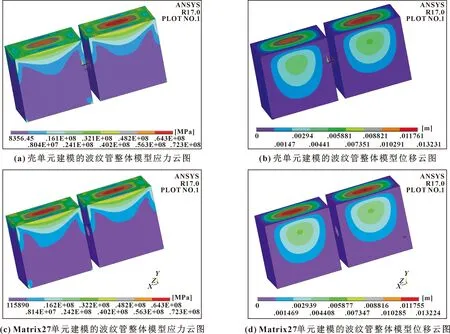
圖5 采用2種不同波紋管模型的整體結(jié)構(gòu)應(yīng)力和位移結(jié)果Fig.5 Stress and displacement results of the whole structure using two different bellows models:(a)stresscontour for shell elements model;(b)displacement contour for shell elements model;(c)stress contour for Matrix27 model;(d)displacement contour for Matrix27 model

4 結(jié)論

(1)基于Matrix27剛度單元對金屬波紋管進行有限元建模，通過有限元分析計算了U形波紋管的軸向剛度和扭轉(zhuǎn)剛度，計算結(jié)果和實體殼單元模型計算結(jié)果以及EJMA經(jīng)驗公式計算值吻合良好。該結(jié)果也與其他研究人員的實驗結(jié)果保持一致。

(2)建立的波紋管簡化模型相較于實體模型的規(guī)模大幅度縮減，在研究含有波紋管的整體系統(tǒng)時尤其方便。該模型可以根據(jù)波紋管工作狀態(tài)如介質(zhì)壓力、溫度等靈活調(diào)整模型自身的剛度屬性，并能應(yīng)用于矩形波紋管和U形波紋管等不同結(jié)構(gòu)，相較于其他波紋管模型具有更好的通用性。該簡化模型有助于有限元技術(shù)在波紋管設(shè)計工作中得到更好的應(yīng)用。