近距離爆破作用下既有襯砌動力響應數值分析

王 偉，江 鴻，袁 青，楊 林，陳培帥

(1.中交第二航務工程局有限公司，武漢 430040；2.中交公路長大橋建設國家工程研究中心有限公司，北京 100088；3.交通運輸行業交通基礎設施智能制造技術研發中心，武漢 430040；4.長大橋梁建設施工技術交通行業重點實驗室，武漢 430040)

隨著我國國民經濟的快速發展，交通基礎設施建設需求量大。特別是山嶺地區，受地形、地質等因素限制，公路隧道改擴建工程大量涌現[1]。考慮線路整體線型及高差條件，一般情況下在建隧道與既有隧道的設計間距較小，在建隧道施工中由于開挖擾動或爆破控制不當等因素往往會造成既有隧道襯砌的開裂及損傷等現象，嚴重威脅著既有隧道的運營安全[2]。因此，如何有效地控制在建隧道爆破對既有隧道的影響，仍然是目前亟需解決的關鍵問題。任登富等[3]依托貴陽地鐵暗挖隧道工程對數碼電子雷管錯峰減振技術進行研究，數碼雷管可精準授時實現各炮孔錯相減振，確保鄰近建筑物的安全；趙志剛等[4]依托大斷面黃土隧道工程，結合現場條件與工程經驗對光面爆破參數進行優化設計，確保了既有隧道安全運營；吳慧等[5]依托某擴建隧道工程，通過精細化炮孔設計控制了爆破振動對既有隧道的危害；林立宏等[6]依托樓山隧道擴挖工程對鄰洞隧道振動衰減規律進行研究，鄰洞隧道迎爆側振動強度大于背爆側，而既有隧道空間對振動衰減效果明顯；蔣楠等[7]依托某緊鄰隧道工程對爆破振動作用下既有襯砌結構動力響應特征進行研究，得出振速峰值衰減經驗公式；汪平等[8]依托京張高鐵隧道工程對小近距隧道爆破下緊鄰既有隧道迎爆側洞內振動信號進行分析，并提出針對掏槽孔的控爆措施。

綜上，目前有關改擴建隧道爆破對既有建(構)筑物的影響研究較多，主要集中在爆破振動對既有結構的影響規律、爆破控制技術等方面，而有關既有結構的動力響應及安全控制標準研究還不全面，缺乏普遍適用性。鑒于此，本文采用現場測試和數值模擬方法研究在建隧道爆破對既有隧道襯砌結構的振動響應，確定適合于該在建隧道爆破對既有襯砌結構的安全控制閾值，確保既有隧道的運營安全，以期為類似隧道施工爆破控制提供借鑒。

1 工程概況及重難點

某在建隧道為單向三車道城市主干道，設計車速50 km/h。隧道長度為630 m，最大埋深為145 m，最大開挖寬度為16.32 m，最大開挖高度為10.45 m，隧道洞身圍巖主要以Ⅴ級強～中風化砂、泥巖為主，呈黃褐色～灰褐色，泥質結構，具有水平層理，層狀構造，局部存在薄層狀構造，遇水易軟化，開挖后不及時支護存在坍塌施工風險，施工開挖時先做好超前支護，部分V級圍巖段現場采用臺階法開挖，上下臺階間距控制在(1～2)D(D為開挖洞徑)。由于在建隧道與既有隧道之間的凈距較小(見圖1)，為27.3 m，按照《公路隧道施工技術細則》[9]的要求，屬于小凈距一般影響程度。為了減小在建隧道在施工時對既有隧道的影響，需要對在建隧道爆破進行嚴格控制。上臺階掏槽孔的形式為傾斜掏槽孔，掏槽孔垂直深度比循環進尺長0.3 m，為1.5 m，炸藥采用2號巖石乳化炸藥，掏槽孔總裝藥量最大為16.80 kg，各類炮孔之間采用毫秒延時爆破，相鄰炮孔時間間隔不小于100 ms。

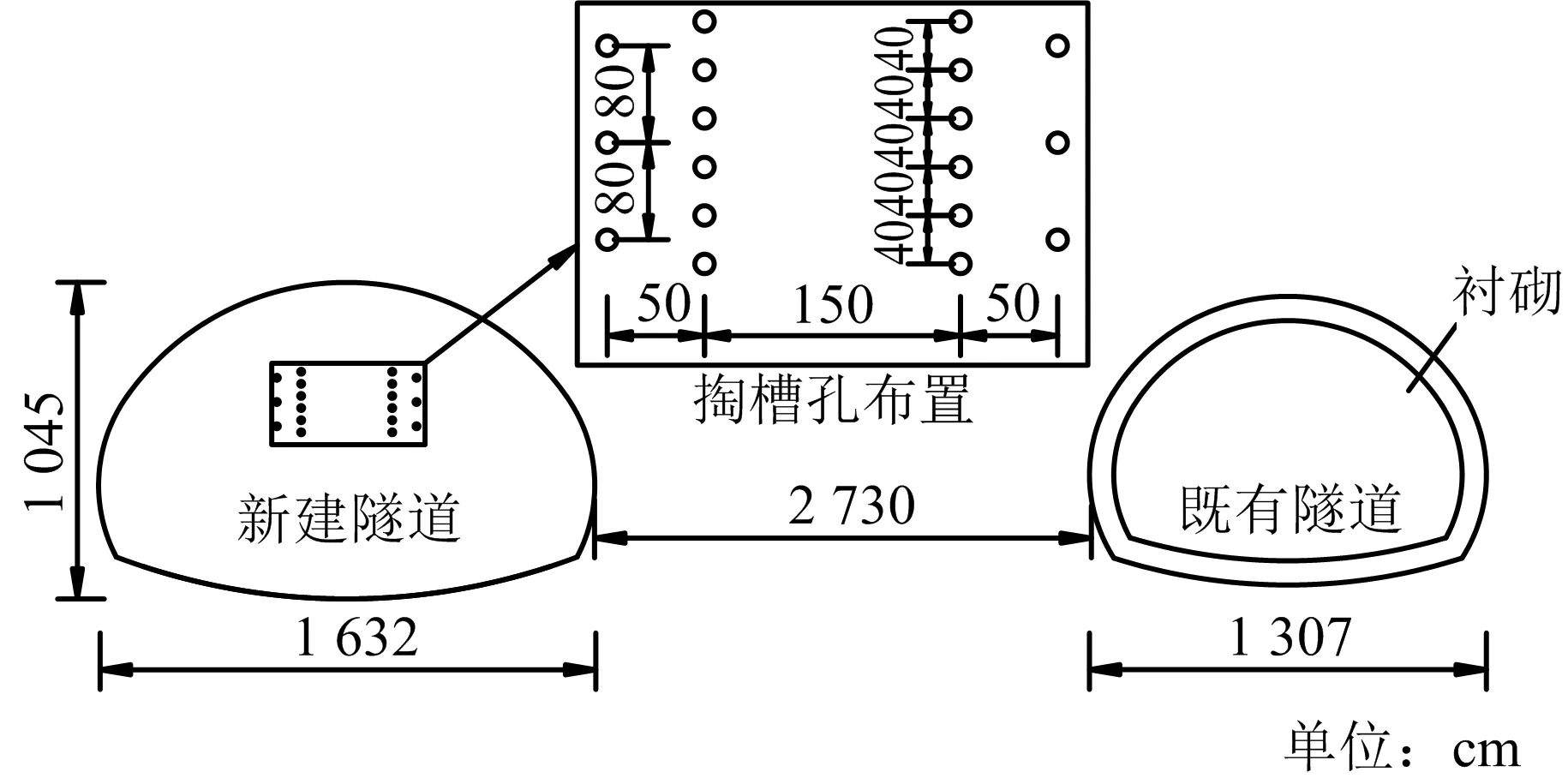
圖1 在建隧道與既有襯砌位置關系

2 數值計算模型

2.1 數值模型建立

為研究在建隧道爆破對既有隧道襯砌結構的動力響應，建立三維數值計算模型，如圖2所示，整個計算模型尺寸為80 m×120 m×80 m(長×寬×高)，其中假設x為水平方向，y為隧道掘進方向，z為垂直方向。模型主要由巖體、既有襯砌、空氣、炸藥4部分組成，均采用Solid164實體單元。為提高計算速度，模型單元劃分時隧道近區網格加密，遠區網格相對稀疏，模型四周及底部均采用無反射邊界，地表采用自由邊界，采用kg-m-s統一單位制。由于在建隧道掏槽孔的裝藥量最大，爆破產生的動力響應越大，爆破分析模型建立時僅考慮掏槽孔爆破作用，炸藥等效作用位于隧道開挖斷面中心位置[10]。

圖2 數值計算模型

2.2 模型參數選取

巖體與既有襯砌視為均質體，采用塑性隨動模型本構關系(*MAT_PLASTIC_KINEMATIC)，部分計算參數如表1所示，其他參數見文獻[11-12]；炸藥采用高能炸藥模型本構(*MAT_HIGH_ EXPLOSIVE_BURN)及相應狀態方程(*EOS_JWL)描述，炸藥模擬參數分別為：V′為初始相對體積，取1.0；A、B、R1、R2、ω為炸藥材料參數，一般通過現場振動測試進行修正，分別取42 GPa、0.44 GPa、3.55、0.16、0.41；炸藥密度ρ取1 100 kg/m3；爆速D取為3 400 m/s；已開挖區域及既有襯砌內部空氣采用空材料模型本構(*MAT_NULL)及相應狀態方程(*EOS_LINEAR_POLYNOMIAL)狀態方程進行模擬，相關參數為：E為初始能量密度，取2.5×106Pa；比體積μ取1.4；狀態方程常數C0～C3、C6取0；狀態方程常數C4～C5取0.4；空氣密度密度ρ取1.25 kg/m3。

表1 巖體及既有襯砌參數

3 數值計算結果分析

3.1 數值模擬對比分析

為保證數值模擬的準確性，通過現場測試結果對數值模擬參數進行修正，現場測試測點布置在與爆破源中心線在同一斷面的既有襯砌迎爆側邊墻位置，如圖3所示。為進一步研究在建隧道爆破對既有襯砌結構的動力響應，分別提取了爆破源同斷面既有襯砌8個不同位置(拱頂、左右拱腰、左右邊墻、左右拱腳、仰拱)的振動速度及爆破影響最大的迎爆側縱向邊墻位置測點的爆破振速，監測點間距為2 m，其中：vx、vy、vz、v合分別代表x、y、z方向振速及三向合振速。

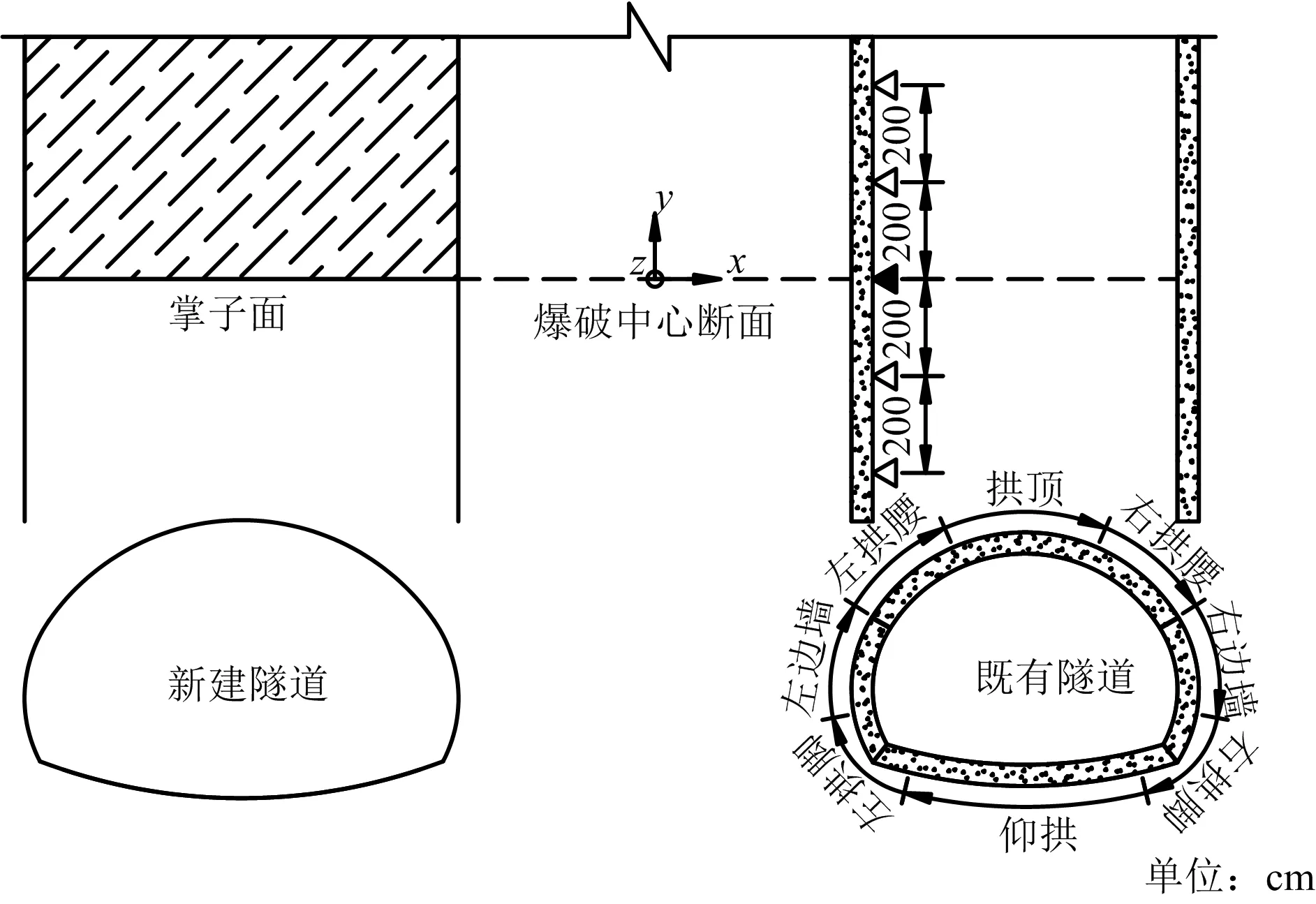
圖3 測點布置

現場測試與數值模擬合振速對比驗證分析如圖4所示。從圖中可以看出，現場測試振速曲線表現出明顯階段性峰值振速，與隧道炮孔裝藥量和所用雷管段位相匹配，各毫秒雷管所對應的階段性振速峰值依次減小，表明隧道爆破開挖由內向外逐層進行，依次為掏槽孔→輔助孔→崩落孔→周邊孔，各炮孔最大段裝藥量也逐級減小。而同一監測點現場測試爆破合振速與數值模擬合振速最大值相接近，相對誤差為4.37%，其中掏槽孔(雷管段位為MS1)爆破振動作用下合振速峰值最大為4.35 cm/s，爆破時程曲線與數值模擬結果基本吻合，說明數值模擬結果能較好地反映現場實際爆破振動影響。

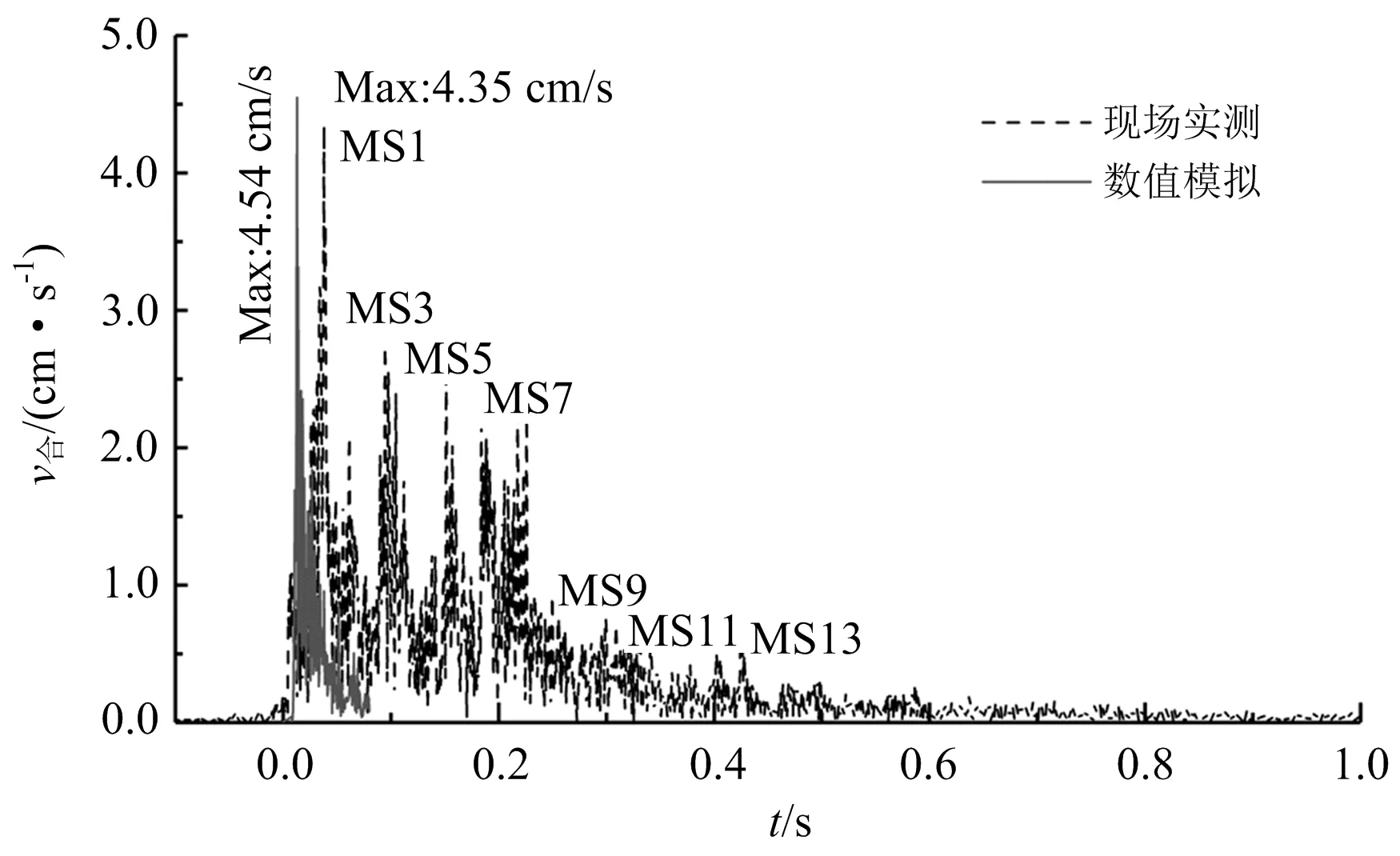
注：MS1～MS13分別表示延時毫秒雷管段別。

3.2 爆破振速分析

既有襯砌合振速分布云圖如圖5所示。從圖中可以看出，隧道爆破振動波首先傳播到與爆破源同斷面的既有襯砌，且既有襯砌迎爆側左邊墻位置先產生振動響應，并形成振動圈沿隧道襯砌逐步向外擴展，在距離最近的迎爆側左邊墻合振速達到最大值(t=12 ms時)，此刻圖中紅色區域代表合振速最大區域，即為爆破振動影響最大位置。隨著時間推移，振動圈逐漸擴大(t=15 ms時)，合振速不斷衰減，合振速峰值呈現先急劇增大，后逐漸衰減的變化趨勢，此刻云圖色譜顏色變淡(t=18、22 ms時)，迎爆側合振速明顯大于背爆側的現象，因此，既有襯砌迎爆側為爆破振動危險區。

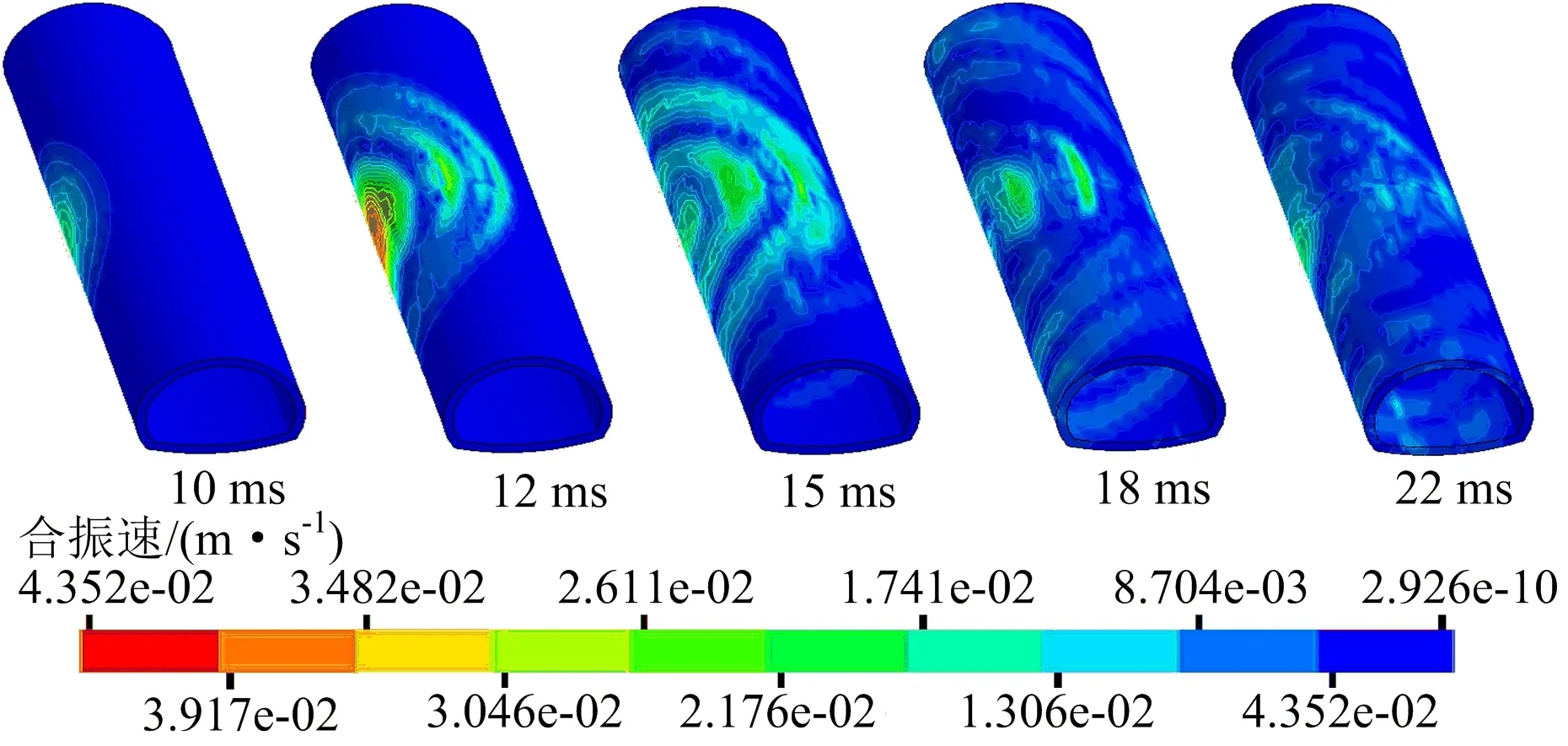
圖5 既有襯砌合振速分布云圖

既有襯砌爆破振速分布規律如圖6所示。從圖6a既有襯砌各向振速分布曲線中可以看出，整體表現出迎爆側位置爆破振速明顯大于背爆側，迎爆側振速約為背爆側振速的4～7倍，其中迎爆側左邊墻位置各向振速均最大，vx、vy、vz、v合分別為4.13、1.83、0.86、4.54 cm/s，其值均小于規范[9]控制標準值8～10 cm/s，而背爆側右邊墻和右拱腳位置爆破振速最小。爆破荷載作用下，既有襯砌結構主要以水平徑向振速(x方向)為主，水平切向振速與垂向振速次之，整體合振速與水平徑向振速變化規律基本一致，且數值相差不大，因此，在監測過程中以水平徑向振速(x方向)峰值大小來評價爆破振動影響程度是合理的。

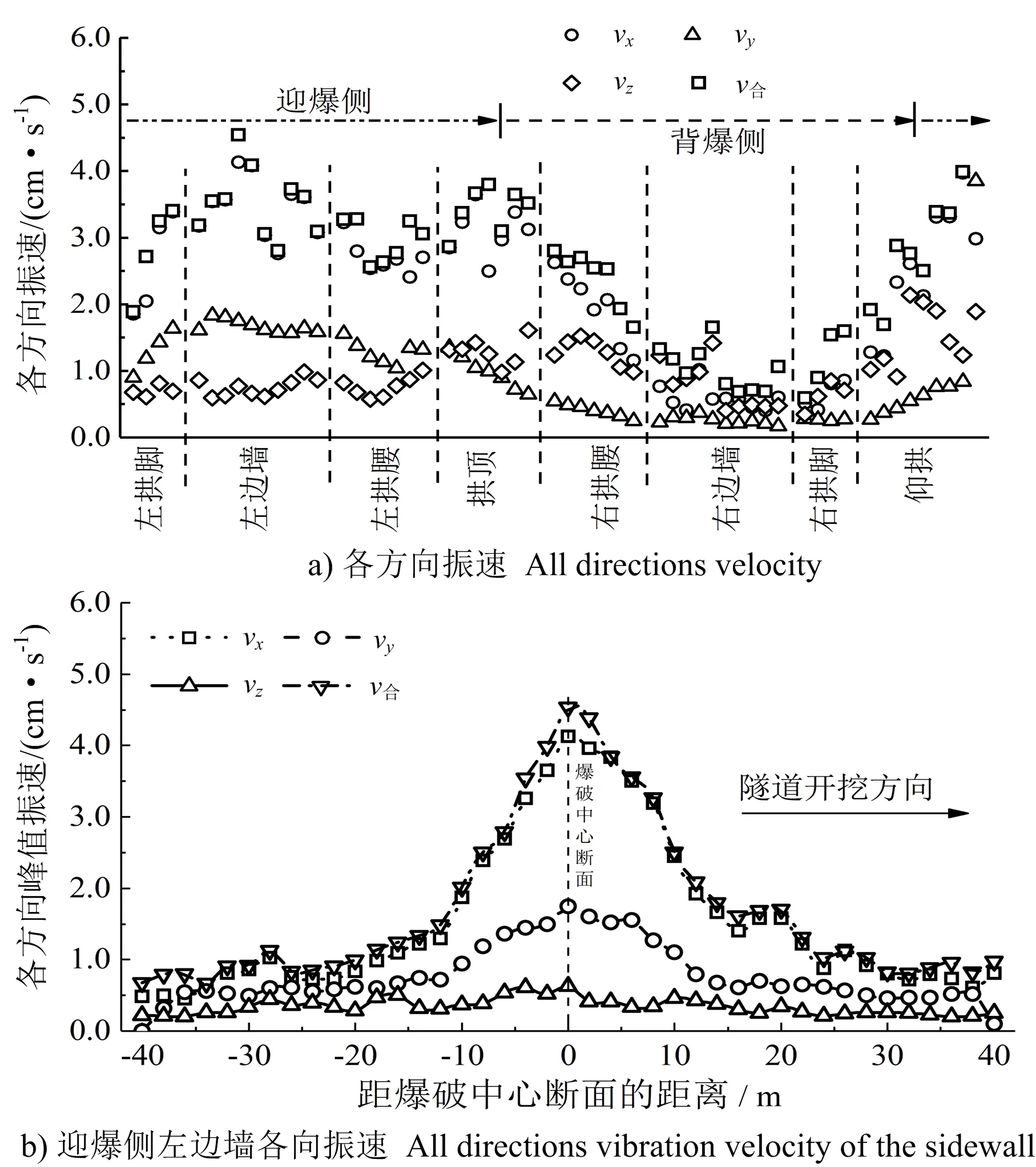
圖6 既有襯砌爆破振速分布規律

此外，既有襯砌左拱腳至左拱腰位置各向振速大小依次為vx>vy>vz，拱頂至右邊墻至仰拱位置各向振速大小依次為vx>vz>vy，從既有襯砌拱頂位置開始迎爆側垂向振速大于水平切向振速，而背爆側則相反，說明迎爆側主要受到爆炸應力波的垂直入射作用，水平徑向振速與水平切向振速表現突出；而背爆側主要受到應力波通過上部拱頂和下部仰拱的繞射作用，水平徑向振速與垂向振速表現較為突出。

為研究迎爆側既有襯砌邊墻位置縱向分布規律，對既有襯砌邊墻位置測點各向振速進行提取(0斷面為與爆破源的位于同斷面的既有襯砌斷面)，如圖6b所示。從圖中可以看出，各向爆破峰值振速基本關于爆破中心斷面呈對稱分布狀態，隨著爆心距的增大而逐漸衰減，在距離爆破中心斷面(1～2)D范圍內各向峰值差振速異明顯，大于此距后各向爆破峰值振速較接近。而已開挖方向既有襯砌迎爆側邊墻位置爆破振速衰減速率略大于未開挖方向，說明已開挖方向掌子面后方由于空洞的存在導致爆破振動傳播過程中爆破能量損失較大，爆破振速減小速率加快。

3.3 爆破應力分析

既有襯砌應力分布云圖如圖7所示。從圖中可以看出，在建隧道爆破作用下，爆炸應力波傳播規律與爆破振速傳播規律相吻合，均由爆破源近區產生逐漸向周圍傳播，先到達既有襯砌迎爆側，后逐漸向背爆側擴散，故迎爆側受到較高的沖擊拉應力，其中最大拉應力主要集中在迎爆側邊墻、拱腳及拱頂位置，最大值為0.41 MPa，因此迎爆側拱腳至拱頂位置在爆破施工過程中應重點監測。

圖7 既有襯砌應力分布云圖

4 結果與討論

綜上分析，爆破荷載作用下既有襯砌結構振速與應力分布規律基本相同。選取了41組迎爆側邊墻位置爆破合振速v合與最大拉應力σt進行線性擬合(見圖8)，可得：

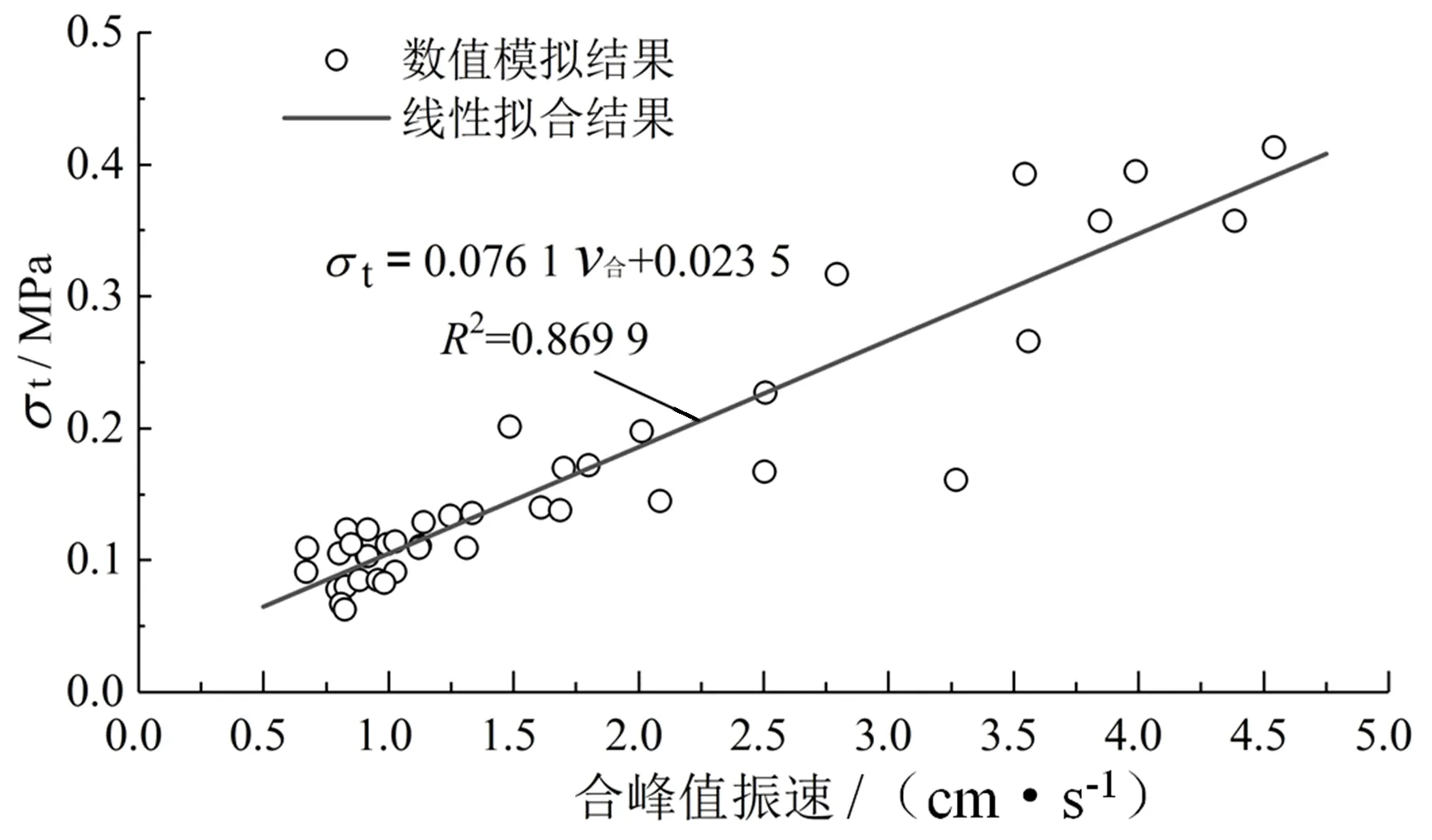
圖8 最大拉應力與合峰值振速擬合

σt=0.076 1v合+0.023 5，R2=0.869 9

(1)

既有襯砌隧道采用50 cm厚的C30鋼筋混凝土，在動荷載作用下既有襯砌抗拉強度會有一定的提高，但考慮爆破損傷及服役年限等不利因素影響，既有襯砌極限抗拉強度取1.30 MPa[13]。為保證既有襯砌結構的運營安全，需要考慮一定安全系數1.7[14]，根據式(1)可得在建隧道爆破條件下，既有襯砌的安全振速閾值為9.87 cm/s。因此，在隧道爆破施工過程中應根據爆破安全振速閾值對爆破參數進行優化控制，避免影響既有襯砌結構的安全。

5 結論

1)掏槽孔裝藥爆破條件下的數值模擬結果與現場測試進行對比驗證，兩者合峰值振速曲線變化規律相吻合，峰值振速較接近，相對誤差僅為4.37%，說明數值模擬結果能夠較好地反映現場爆破振動響應。由于不同炮孔之間的裝藥量和延時雷管段別存在較大差異，現場測試峰值振速曲線表現出明顯的階段性。

2)爆破荷載作用下既有襯砌迎爆側峰值振速明顯大于背爆側，約為背爆側的4～7倍，其中迎爆側邊墻位置峰值振速最大，而背爆側邊墻及拱腳位置振速相對較小，且主要以水平徑向振速為主，因此，爆破振動監測以水平徑向峰值振速大小來評價爆破振動影響程度也是合理的。迎爆側邊墻位置縱向振速分布表現為隨著爆心距的增大而逐漸減小，距離爆破中心斷面(1～2)D范圍內各向峰值振速存在較大差異，而后較接近。

3)既有襯砌最大拉應力與爆破峰值振速分布規律基本一致，通過線性擬合建立了爆破峰值振速與最大拉應力之間的關系式，確定既有襯砌的安全振速閾值為9.87 cm/s，因此，應根據此安全振速閾值對爆破施工進行控制。