優化迭代步長的兩種改進增量諧波平衡法1)

黃建亮 張兵許 陳樹輝

(中山大學應用力學與工程系,廣州 510275)

引言

增量諧波平衡法(incremental harmonic balance,IHB) 是一個半解析半數值的方法,由Lau 和Cheung[1]于1981 年提出以來,是把增量過程牛頓-拉弗森(Newton-Raphson)迭代過程和諧波平衡過程(伽遼金(Galerkin)平均過程)兩者有機地結合起來,已被成功地推廣應用于非線性振動的各個領域.Lau[2]和陳樹輝[3]分別于1995 年和2007 年對該方法的發展及其應用做了很好的綜述.在文獻[3-4]中,IHB 法已被總結為具有兩大優點:(1)應用于分析強非線性振動問題,并得到高精度解;(2)是一類求解非線性微分方程的計算方法,適用于大范圍參數變化的定量分析.

IHB 法已廣泛應用在工程中的各個領域,包含航空航天、車輛交通、海洋工程、機械等各種非線性振動問題的分析中[5-8].Wang 和Zhu[9]建立了非圓鏈輪的汽車皮帶傳動系統的動力學模型,用IHB法研究減小凸輪軸角度變化的效果.Mitra 等[10]利用IHB 法分析了強非線性半潛式平臺系統的主諧波響應和高階次諧波響應.在機械振動中,齒輪的振動被廣泛研究,Li 等[11]分析了具有動態齒隙的齒輪副系統在內外周期激勵下的非線性動力學特性;Zhou 等[12]基于IHB 法分析了考慮齒隙、阻尼、傳動誤差和嚙合剛度的直齒圓柱齒輪副動力學模型,發現了跳躍不連續現象和多個穩定解共存.IHB 法對各種動力學問題具有良好的求解效果.Wang 等[13]將非線性波傳播問題的控制方程轉換為相應的具有多個時滯的非線性時滯微分方程,并應用IHB 法進行計算,大大簡化推導的過程和計算的時間.Cheng 等[14]應用IHB 法分析了附加恒力對準零剛度隔振器的主共振和1/3 次諧波共振的影響.Li 和Chen[15]利用IHB 法研究了空氣壓縮機模型的周期運動,混沌運動和分岔行為.Karli?i?等[16]利用IHB 法分析了基于馬蒂厄-達芬(Mathieu-Duffing)非線性振子模型的非線性壓電能量采集器的穩態響應.Shen 等[17]用IHB 法研究了馬蒂厄-達芬振子的分岔和混沌路徑,識別出了一系列振子的倍周期分岔點,發現它們近似服從普適標度律.IHB 法也被應用于分數階非線性方程的計算過程中,Shen 等[18]將IHB 法應用到分數階非線性振子的動力學分析中,建立了該振子周期解的一般形式來獲得高精度的解.對于振動系統里含有多個不可約頻率的準周期運動問題,Huang 等[19-21]將IHB 法發展成為多時間尺度IHB 法,應用于求解含邊頻帶的準周期運動,自動跟蹤非線性系統的準周期運動頻率響應.竇蘇廣等[22]和蘇鸞鳴和葉敏[23]將IHB 法應用于非線性系統參數識別,分析了在周期、分岔和混沌等復雜運動狀態下的參數識別,并驗證了IHB 法相對于其他方法有明顯的抗噪性能.此外,他們還將增量諧波平衡非線性識別理論運用到實驗建模方法中[24-25].

為了提高IHB 法適應性,人們對它進行了各種改進,主要集中在兩個方面.第一方面是要提高IHB 法的計算效率.Wang 和Zhu[26]對非線性代數方程的余項使用快速傅里葉變換逼近,非線性代數方程的雅可比矩陣使用Broyden 擬牛頓迭代方法逼近,從而提高了諧波平衡過程的收斂速度;第二方面是解決系統響應曲線在峰值(或拐點)處的自動跟蹤問題.為了可使IHB 法能更好的追蹤響應隨參數變化情況,特別是在峰值(或拐點)處自動跟蹤,避免出現迭代不收斂的問題,可利用弧長延拓法對IHB 法進行改進[4,26-27].另外,Zheng 等[28]在線性增量過程中引入Tikhonov 正則化來解決迭代中的不適定問題,從而改變IHB 法的收斂性能.然而對IHB 法的各種改進,沒有涉及到如何選擇初值條件的問題,在給定的初值條件有時并不能保證IHB 法的收斂性.

在IHB 法的牛頓-拉弗森迭代過程中,初值可以任意設定,實際上IHB 法的牛頓-拉弗森迭代過程相當于對初值進行多次嘗試,并不能保證初值的收斂與否,當迭代的誤差增大時相當于換一個初值進行重新迭代嘗試.本文針對這一問題,引入回溯線搜索(backtracking line search,BLS)優化算法[29]來調節IHB 法的收斂步長,使步長逐漸減小直至滿足弱沃爾夫(Wolfe)條件,即下降性條件,來對初值進行迭代計算.在此基礎上,引入迭代負梯度方向,再利用迭代優化算法狗腿法(dogleg method)[30]的思想,加快其收斂速度,提高了初值嘗試的局部收斂范圍,從而提高了IHB 法牛頓-拉弗森迭代的收斂性.

1 傳統的增量諧波平衡法

考慮一個一般形式的n維非線性振動系統,可表示為如下平衡微分方程

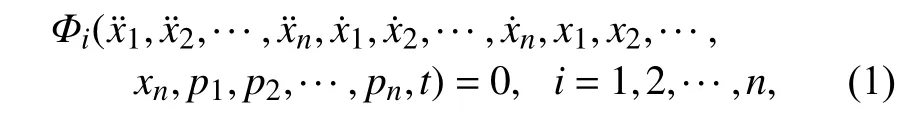
其中,“·”表示對時間t的微分,xi(t) 是位移變量,pi表示第i個外激勵,Φi是二階的非線性常微分方程.引入新的時間變量 τ,定義為

其中,ω 為系統的振動響應頻率.方程(1)可表示為

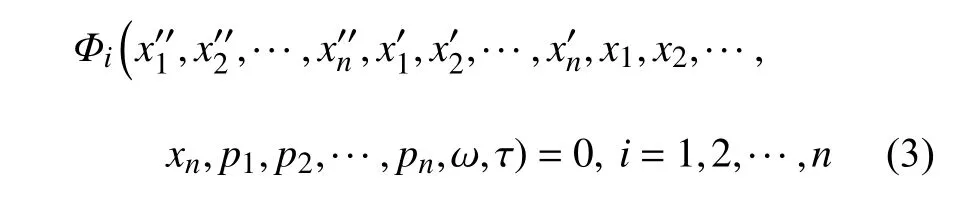
其中,“ ′ ”表示對時間 τ 的微分.

IHB 法的第一步是增量過程,即牛頓-拉弗森迭代過程.設xi0,pi0和 ω0是方程(3)的解,則其鄰近解可用增量形式表示為

其中,Δxi,Δpi和Δ ω 為增量.把方程(4) 代入方程(3),并略去 Δxi,Δpi和 Δ ω 的高階小量,得到了線性化的增量方程

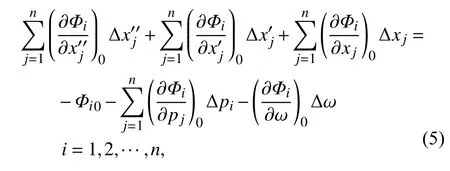
其中,下標0 表示為函數增量的初值.方程(5)可表示為矩陣形式

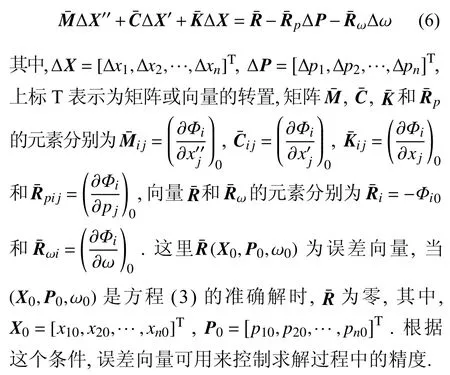
IHB 法的第二步是諧波平衡過程,即伽遼金平均過程.將n維非線性系統的穩態解及其增量都展開成傅里葉級數

其中,nc和ns是正整數,表示諧波項項數;Cs,Ai和ΔAi分別表示為

那么向量X0及其增量可分別表示為傅里葉系數向量A及其增量ΔA

積分上式并整理歸并為以 ΔA,Δ ω 和 ΔP為未知量的代數方程組

這里,KA和Rp是nt×nt的矩陣,R和Rω是nt×1 的列向量,nt=n×(nc+ns) .當要分析某一固定外激勵幅值下的頻率響應曲線時,在方程(14)中取P為固定值,即 ΔP=0,那么方程(14)變成

當要分析某一固定外激勵頻率下的各響應幅值隨外激勵幅值變化的響應曲線時,在方程(14)中取ω為固定值,即 Δ ω=0,那么方程(14)變成

在用傳統的IHB 法對方程式(19)或式(20)的求解過程中,要給定一個假定的初值,然后可先利用諧波平衡過程再利用增量過程,或也可先利用增量過程再利用諧波平衡過程,追蹤出所有的解.在增量過程中,可應用頻率增量,振幅增量,或弧長增量,具體可參見文獻[3-4].

如上所述,在用傳統IHB 法求解過程中,事先要給定一假定的初值,因此涉及到給定初值的選取問題.一般說來,當碰到這類問題時,一般是用三種途徑來解決:(1)憑IHB 法使用者的經驗,事先給定一接近于精確解作為IHB 法的初值;(2)以線性化系統得到的解作為IHB 法的初值;(3)利用攝動法等求得小參數范圍內的弱非線性振動的解作為IHB 法的初值.在傳統IHB 法用牛頓-拉弗森迭代過程中,如給定的初值在通往收斂的路徑上,那么解就會收斂至精確解,即此初值點是在其收斂范圍內.為了擴大初值點的選擇范圍,在用牛頓-拉弗森迭代過程中,本文將對迭代的增量進行兩個方面的改進.

2 引入BLS 優化算法的改進增量諧波平衡法(GIHB1)

其中,向量KAk和Rk分別表示KA和R在第k次迭代的結果.

現對傳統IHB 法中的迭代增量進行改進.首先,引入目標函數

當 ‖R‖→0 時,f(A)→0 .再引入一次函數和基于Cauchy-Point 的二次函數

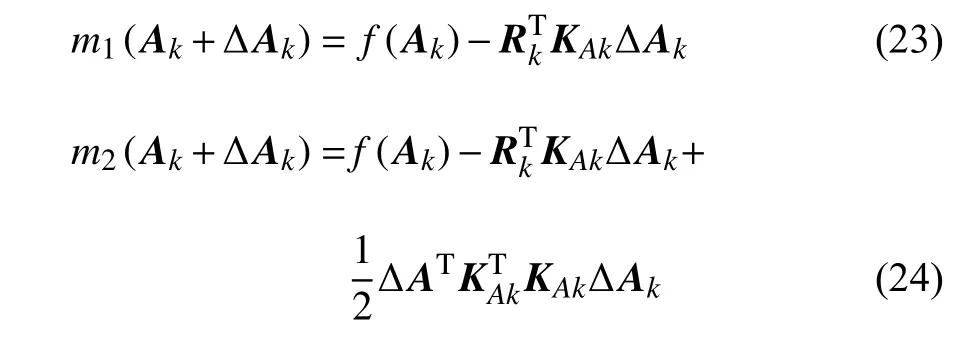
其中,向量Ak表示A在第k次迭代的結果.

當初值選擇恰當時,‖ ΔA‖ 越小,對f(Ak+ΔAk)在點Ak上進行模擬,m2(Ak+ΔAk) 與f(Ak+ΔAk) 的差越小.在迭代過程中,用m2(Ak+ΔAk) 代替f(Ak+ΔAk)進行求解,則增量變為

當KAk為非奇異矩陣時,等價于原牛頓-拉弗森迭代增量式(21),即使得迭代一步就到達m2(Ak+ΔAk)最小點.

當初值選擇不當時,可導致 ‖ ΔA‖ 較大,m2(Ak+ΔAk) 代替f(Ak+ΔAk) 吻合度較差,因此導致f(Ak+ΔAk) 的值不降反增,從而導致迭代不收斂.對此,引入BLS 優化算法將其迭代步長進行改進,以為牛頓-拉弗森迭代方向,由于

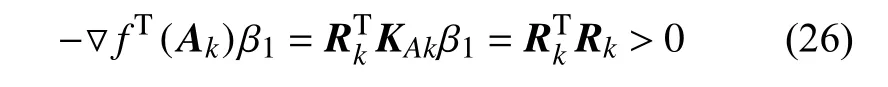
因此牛頓-拉弗森迭代的方向 β1與負梯度方向呈銳角,滿足方向下降條件.在 β1前乘以系數 α ,當α較小時,滿足弱Wolfe 條件時

即可選定迭代步長,然后再進行IHB 法的第二步諧波平衡過程(Galerkin procedure),其中,常數c通常較小,一般可取c=1.0×10-4,該優化算法的迭代過程如圖1 所示.在圖1 的算法中,為了保證較快的迭代速度,取 α =1 為牛頓-拉弗森迭代的初值,ρ在每次迭代時與 α 相乘,為了保證步α β1逐漸減小,取 0 ＜ρ ＜1 .隨著迭代次數的增加,α 值逐漸減小,即A的增量 α β1逐漸減小,直至滿足弱Wolfe 條件,然后跳出循環,以得到Ak為初值,重新執行牛頓-拉弗森迭代過程.

圖1 結合Backtracking line search (BLS)優化算法的IHB 法(GIHB1)Fig.1 Algorithm for a generalized IHB method with backtracking line search (BLS) method (GIHB1)

3 引入狗腿法思想并結合BLS 算法的改進IHB 法(GIHB2)

為了加快BLS 算法的迭代運算速度,應用狗腿法的思想,在此過程中加入兩個調節參數用于控制迭代方向.當 ‖ ΔA‖ 較小時,為負梯度方向,即最快的下降方向.m2(Ak+ΔAk) 在 β2方向上的最小值對應的系數 αmin可由

系數 αmin的主要作用是調節負梯度方向的步長,使得該步長和模擬函數牛頓-拉弗森迭代的步長處于同一個量級.在狗腿法思想基礎上,引入兩個調節參數 α1和 α2用于加快BLS 算法的迭代運算速度.令Ψ1k=α1αminβ2,Ψ2k=β1,其中,α1是調節目標函數f(Ak) 和二次模擬函數m2(Ak+ΔAk) 的迭代方向,α1∈(0,0.1) .當 ΔA沿 著 0 →Ψ1k→Ψ2k方向時,m2(Ak+ΔAk) 逐 漸下降到最小值,其中 0 表示為零向量.

引入函數

用于調節迭代的方向,其中,α2起線性化分割的作用,其值可取 α2∈(0,0.1) .同時,引入m2(Ak+ΔAk)與f(Ak+ΔAk) 的擬合系數 ρk,可表示為

此系數 ρk越大時,m2(Ak+ΔAk) 與f(Ak+ΔAk)的吻合程序越高,f(Ak+ΔAk) 越滿足下降條件.算法的迭代過程可利用系數 ρk值的大小來判斷 α 是否滿足條件.對于系數 ρk界定一個閾值 ρ0,當 ρk＞ρ0時,系數 α 滿足條件;否則繼續減小,直至滿足ρk＞ρ0,該算法的迭代過程如圖2 所示.

在圖2 所示的算法中,α =1 時迭代方式為牛頓-拉弗森迭代,α 與F(α) 的模長有正相關的關系.隨著迭代次數的增加,α 值逐漸減小,即A的增量F(α) 的模長逐漸減小,直至 ρk＞ρ0,然后跳出循環,得到初值Ak,然后重新執行牛頓-拉弗森迭代過程.

圖2 結合BLS 算法和狗腿算法的改進IHB 法(GIHB2),其中在狗腿算法的函數 F (α) 中引入2 個調節參數 α 1 和α2Fig.2 Algorithm for a generalized IHB method (GIHB2) combined with BLS method and dogleg method that contains two parametersα1 and α2 in the functionF(α)

值得注意的是上述兩種改進的IHB 法隨著 α 的減小,迭代效率會逐漸降低,當 α ＜10-6時,即認為迭代不收斂.為了提高收斂性的同時,提高迭代的效率,在算法實現過程中,可設 α 的下界值為0 .01,若α ＜0.01 ,則令Ak+1=Ak+0.1β1改變初值,重新執行算法的迭代過程.

4 算例

利用3 種IHB 法,即傳統的IHB 法、結合BLS 算法的GIHB1 法和引入狗腿思想并結合BLS 算法的GIHB2 法,對兩個算例的初值問題進行分析,一個是經典的單自由度范德波爾(van der Pol)振蕩,另一個是耦合的兩自由度范德波爾振蕩.在IHB 法的求解過程中,此二類范德波爾振蕩的極限環周期解依賴于給定的初值條件.為了檢驗上述3 種IHB 法計算結果的準確性,本文采用四階龍格-庫塔(Runge-Kutta,RK)數值法作為比較.四階R-K數值法是直接對微分方程采用時間積分法,它可以較準確地給出系統某一時刻的位移、速度和加速度的數值.

4.1 van der Pol 振蕩

單自由度van der Pol 振蕩方程為

其中,“·”表示對間t的導數,參數 λ 在區間 [ 0,1.0] 內取值用來分析系統響應的霍普夫分岔.當單自由度van der Pol 振蕩方程(32)中的2 個參數 ε 和 λ 確定時,該振蕩方程具有唯一一個極限環.這類van der Pol 振蕩方程在航空航天、力學以及電子等工程領域都有很廣泛的應用.例如,Motta 和Malzacher[31]發展了湍流經過機翼面的van der Pol 模型,根據此模型構建了開環與閉環的流量控制.Akhtar 等[32]提出了水動力作用在圓柱/橢圓柱結構上的范德波爾-達芬振蕩模型,用此模型得到的計算結果與CFD 的結果一致.Facchinetti 等[33]基于van der Pol 振蕩方程研究了在渦振中結構與波的耦合振蕩.

值得注意的是,經典攝動法只能適用于 ε 為小參數時van der Pol 振蕩方程的求解,而不適用于大參數時的求解.Burton[34]說明了當 ε ＞1.0 時,利用攝動法去求解會得到錯誤的結果.而IHB 法的優勢是不僅適用于弱非線性系統,也適用于強非線性系統,不失一般性,文中 ε 可取大參數作為分析.

引入新的時間變量

方程(33)變為

其中,“ ′ ”表示為時間變量 τ 的導數.

因方程(34)只含奇次項,系統是對稱的振蕩響應,可將x展開為含有m個奇次諧波項的傅里葉級數

根據式(14),得

其中,KA是 2m×2m的矩陣,對應于傅里葉系數向量

向量R和Rω可分別由式(16)和式(17)計算得到.在本文中取誤差向量R的模 ‖R‖ 小于1 .0×10-7作為IHB 法諧波平衡過程的收斂條件.

顯然,式(36)中所含的未知量的數目比方程的數目多2 個,由于系統響應頻率 ω 是未知的,因此必須選定 Δ λ 為主動增量,再選定式(37)中的某一諧波項系數為參考量,如b1,那么該參考量的增量為零,即 Δb1=0,這樣方程(36)就可求解.具體步驟可參見文獻[3-37]等.

現利用上述3 種方法分別對van der Pol 振蕩方程(32)求解,其中,λ =0.87 ,ε =5.0 ,選定b1為參考量.同時,在式(35)中取諧波項項數為m=25 .圖3所示為在取不同初值時用3 種方法得到的誤差‖R‖與迭代次數的關系.從圖中可以得到:

(1)圖3(a)中選定初值為頻率 ω0=0.58,諧波項系數a1=1.0 ,b1=1.0,其余諧波項系數設為零,可以看出傳統的IHB 無法收斂,另外兩種改進方法均可收斂,GIHB1 法經25 步迭代達到‖R‖＜1.0×10-7的收斂條件,GIHB2 法經23 步迭代達到收斂條件,其響應頻率為 ω =0.5877 ;

圖3 不同初值條件下用3 種IHB 法求解van der Pol 振蕩方程(32)迭代收斂情況,其中,ε =5.0 ,λ =0.87 .初值分別為:(a) ω 0=0.58 ,a 1=1.0 ,b 1=1.0 ;(b) ω 0=0.58,a 1=1.0,b 1=1.4 ;(c) ω 0=0.58,a 1=1.8,b1=-0.7Fig.3 Iteration convergence of solution of van der Pol Eq.(32) with different initial values using the three IHB methods,where ε =5.0,λ=0.87 .Initial values are (a) ω 0=0.58 ,a 1=1.0 ,b 1=1.0 ;(b) ω 0=0.58 ,a 1=1.0,b 1=1.4 ;(c) ω 0=0.58 ,a 1=1.8,b1=-0.7

(2)圖3(b)中選定初值為頻率 ω0=0.58,諧波項系數a1=1.0 ,b1=1.4,其余諧波項系數設為零,可以看出三種方法都可收斂,傳統IHB 法誤差 ‖R‖ 先增大再減少,其最大值可達到3113,然后開始下降,在誤差增大過程中,增量的模長較大,易出現跳出牛頓-拉弗森迭代的現象,導致整個迭代不收斂.而對改進后的兩種方法來說,誤差 ‖R‖ 可一直保持減少,直至滿足迭代條件.可以看出傳統IHB 法需要28 步迭代達到收斂條件,而改進后的兩種GIHB 法分別只需要25 步和15 步迭代達到收斂條件;

(3)圖3(c)中選定初值為頻率 ω0=0.58,諧波項系數a1=1.8 ,b1=-0.7,其余諧波項系數設為零,可以看出傳統IHB 法無法收斂,兩種改進GIHB 法均可收斂,GIHB1 法經214 步迭代才能達到收斂條件,而GIHB2 法只需58 步迭代即可達到收斂條件.

圖4 所示為用3 種IHB 法求解van der Pol 振蕩方程(32) 的初值a1和b1的選定范圍,其他初值為ω0=0.58 及諧波項系數除值a1和b1外都為零.可以看出,兩種改進后的方法其初值的選定范圍一樣,且均多于傳統IHB 法的初值選定范圍.圖5 所示為取λ=0.87,ε =5.0 時van der Pol 振蕩方程(32)的極限環,可以看出3 種IHB 法求出的結果是一致的,是因為兩種改進的GIHB 法只涉及到增量過程的改進,而諧波平衡過程沒有改變;同時3 種IHB 法求得的結果與用四階R-K 法求得的數值結果高度吻合.

圖4 用3 種IHB 法求得van der Pol 振蕩方程(32)解的初值 a1 和b1的選定范圍,其他初值為 ω 0=0.58 及其他諧波項系數設為零Fig.4 The regions for the initial value for a1 and b1 of solutions of van der Pol Eq.(32) using the three IHB methods,the other initial value for frequncy is ω 0=0.58 and the other initial harmonic terms are set to be zero

圖5 用3 種IHB 法和四階龍格-庫塔數值法求得范德波爾振蕩方程(32)的解,其中 λ =0.87 和ε=5.0Fig.5 Solutions of van der Pol Eq.(32) by the three IHB methods and numerical integration using the fourth-order R-K method,where λ=0.87 andε=5.0

4.2 耦合van der Pol 振蕩

眾多學者對工程中出現的耦合van der Pol 振蕩的動力學特性感興趣.Barron 和Sen[35]考慮了在一質量-彈簧結構上4 個耦合van der Pol 振蕩的同步性.Siewe 等[36]從實驗上分析了在非線性與時滯耦合的兩個van der Pol 振蕩的同步性,實驗得到的結果與理論分析相一致.現考察兩自由度耦合van der Pol 振蕩方程[37-38]

其 中,μ1=-0.1 ,μ2=0.5 ,γ1=0.1 ,γ2=0.08 .同樣 利用IHB 法求解這類強非線性耦合振蕩系統,引入新的時間變量 τ =ωt,方程變為

因方程(39)只含有奇次項,系統是對稱的振蕩響應,可將x1和x2展開為含有m個奇次諧波項的傅里葉級數

其中,m=10 .根據式(14),同樣可得方程(36),其中,KA是 4m×4m的矩陣,對應于傅里葉系數向量

同樣選定 Δ λ 為主動增量,再選定式(41)中的諧波項系數b11為參考量,那么該參考量的增量為零,即 Δb11=0 ,根據方程(36)即可得在不同參數 λ 下系統響應的頻率 ω ,即 λ -ω 響應曲線.在此例中,給定不同的初值,利用IHB 法會得到不同的 λ -ω 響應曲線.設選定初值為ω0=1.0

其中,l為取1 的個數,m-l表示取0 的個數.圖6 表示耦合van der Pol 振蕩方程(38)在其系數 μ1=-0.1,μ2=0.5,γ1=0.1 和 γ2=0.08 ,初值條件為 ω0=1.0 和式(42)下,3 種IHB 法計算所得的系統頻率 ω 與參數 λ 的對應關系曲線(ω -λ),在這些曲線上的每一點就對應系統的一個極限環.在圖6 中,3 種IHB 法都可求得系統響應頻率 ω ≈1.0 附近的 ω -λ 關系曲線,兩種改進的GIHB 法可求得系統響應頻率ω ≈0.67 和ω ≈0.3 附近的的ω -λ 關系曲線,而結合狗腿法和BLS 算法的GIHB2 法還可求得系統響應頻率 ω ≈0.4 和 ω ≈0.2 附近的的 ω -λ 關系曲線.表明了兩種改進后的GIHB 法相比傳統的IHB 法有更廣的初值選定范圍,得到了傳統IHB 法較難求得的解,特別是結合狗腿法和BLS 算法的GIHB2 法可以得到系統解的全貌.值得一提的是:進一步研究表明,在 ω ≈1.0 附近的 ω -λ 關系曲線有一半的點對應的極限環是穩定的,另一半對應的極限環是不穩定的;其余4 條曲線對應的極限環也是不穩定的.

圖6 不同初值條件下用3 種IHB 法求得耦合范德波爾振蕩方程(38)的解,其中,μ 1=-0.1 ,μ 2=0.5 ,γ 1=0.1 和γ2=0.08Fig.6 The solutions of coupled van der Pol Eq.(38) with different initial values using the three IHB methods,where μ 1=-0.1 ,μ 2=0.5,γ1=0.1 ,andγ2=0.08

圖7 所示為不同初值條件下用3 種IHB 法求解耦合van der Pol 振蕩方程(38)在 ω ≈1.0 附近迭代收斂情況,其中,λ =0.08 ,μ1=-0.1,μ2=0.5 ,γ1=0.1和 γ2=0.08 .圖7(a)中選定初值為頻率 ω0=1.0,諧波項系數取式(42)中的l=7 ,b11=0.7,可以看出三種方法都可收斂,傳統IHB 法誤差 ‖R‖ 在前10 迭代過程中在 [ 0,100] 間波動,然后開始下降,達到收斂條件.用兩種改進的GIHB 法得到的誤差 ‖R‖ 一直減少,直至滿足迭代條件.看出傳統IHB 法需要18 步迭代達到收斂條件,而兩種改進的GIHB 法分別只需要12 步和10 步迭代達到收斂條件.圖7(b)中選定初值為頻率 ω0=1.0 ,諧波項系數取式(42)中的l=8,b11=0.8,可以看出傳統IHB 法在迭代的前10 步過程中波動,第11 步誤差徒然變大,之后迭代不收斂.而兩種改進的GIHB 法得到的誤差 ‖R‖ 一直減少,直至滿足迭代條件.改進后的GIHB1 法和GIHB2 法分別只需要14 步和11 步迭代達到收斂條件.圖8所示為取λ =0.08 ,μ1=-0.1 ,μ2=0.5 ,γ1=0.1 和γ2=0.08時耦合van der Pol 振蕩方程(38)的極限環,可以看出3 種IHB 法求得的結果一致,并與用四階R-K 法求得的數值結果高度吻合.

圖7 不同初值條件下用3 種IHB 法求解耦合van der Pol 振蕩方程(38)在 ω ≈1.0 附近迭代收斂情況,其中,λ =0.08 ,μ 1=-0.1,μ2=0.5,γ 1=0.1 和γ2=0.08Fig.7 Iteration convergence of solution of coupled van der Pol Eq.(38)near ω ≈1.0 with different initial values using the three IHB methods,where λ =0.08 ,μ 1=-0.1 ,μ 2=0.5 ,γ 1=0.1 ,andγ2=0.08

圖8 用3 種IHB 法和四階龍格-庫塔數值法求得耦合van der Pol 振蕩方程(38)的解,其中,λ =0.08 ,μ 1=-0.1 ,μ 2=0.5 ,γ 1=0.1 和γ2=0.08Fig.8 Solutions of coupled van der Pol Eq.(38) by the three IHB methods and numerical integration using the fourth-order R-K method,where λ =0.08 ,μ 1=-0.1 ,μ 2=0.5 ,γ 1=0.1,and γ2=0.08

5 結論

針對傳統IHB 法遇到的初值選擇問題,本文提出了兩種改進的IHB 法,第一種是引入BLS 優化算法的改進IHB 法(GIHB1),其目的是為了調節IHB 法的迭代步長;第二種是在第一種改進的基礎上再結合狗腿法思想的改進IHB 法(GIHB2),其目的是為了調節迭代方式,使迭代方向沿著較快的下降方向,從而加快BLS 算法的迭代運算速度.兩個自治系統的算例說明了兩種改進IHB 法的有效性,第一算例表明兩種改進的IHB 法的初值選擇范圍遠大于傳統IHB 法的初值選擇范圍,且GIHB2 法在一些情況下求得解的收斂步數遠少于GIHB1 法;第二個算例表明在給定的初值條件下,傳統的IHB 法只能得到1 條 ω -λ 關系曲線,GIHB1 法可以得到3 條ω-λ關系曲線,而結合狗腿法思想的GIHB2 法可以得到5 條 ω -λ 關系曲線,同樣地,GIHB2 法求得解的收斂步數也小于GIHB1 法.另外,兩種改進的GIHB 法只是改進了增量過程,而沒有改變諧波平衡過程,計算的結果與傳統IHB 的結果是一致的,所以兩種改進的GIHB 法對于非自治系統的分析也是有效的.綜上,引入BLS 優化算法再結合狗腿法思想的GIHB2 法在解決初值問題上是傳統IHB 法的有效補充,可進一步推廣至高維非線性振動系統上.