基于數值模擬正交試驗的采空區穩定性因素的敏感性分析

何榮興，韓智勇，劉 洋，張 晶，鄒開華

(1.東北大學資源與土木工程學院，遼寧 沈陽 110819；2.內蒙古科技大學礦業研究院，內蒙古 包頭 014010)

地下礦產資源采出后形成采空區，采空區周圍巖體的力學平衡被打破，在重力和次生應力作用下，會產生裂隙和變形。采空區的長期存在使一些礦區的地壓活動加劇，相繼從局部崩落發展到大范圍的突然崩落，引起地表大范圍的巖移，造成了嚴重的破壞。目前，采空區已成為金屬非金屬礦山安全生產的主要危險源[1]，因此準確評估采空區穩定性狀態，對于確定采空區處理方法和處理時機具有重要的指導意義。

目前，采空區穩定性評價方法主要有定性分析法、定量分析法、現場監測分析法等。采空區變形破壞總是在若干特定影響因素作用下產生的，而每一個影響因素又由若干因子組成，采空區穩定性受多種因素制約，各因素間又相互關聯，決定了采空區穩定性評判是一個復雜的系統工程。因此，越來越多的學者采用數學方法對采空區穩定性進行綜合評價[2-9]。在建立評價體系中，采空區穩定性因素的影響權重確定方法主要是專家打分法和1～9標度法，但二者均帶有一定的主觀性，影響采空區的評價結果。確定各影響因素的敏感性對確定復雜采空區失穩主控因素及相應的臨界值并設計采場結構參數、為采空區穩定性綜合評判體系構建過程中權重確定具有十分重要意義。國內外學者在此領域開展了大量研究工作。宋衛東等[10]從礦柱載荷、強度、失穩形式及影響因素四個方面推導出2種礦柱的安全系數計算公式，采用6因素、5水平正交試驗分析礦柱穩定性影響因素的敏感性，并研究主要影響因素與礦柱安全系數之間的關系。 尹升華等[11]建立計算矩形礦柱安全系數的簡化公式，采用正交極差分析對礦柱穩定性影響因素的敏感性進行評價，得到礦房寬度、礦柱寬度與礦柱安全系數間的關系曲線。隨著計算機技術的發展，數值模擬在多方案理論研究方面具有明顯優勢，數值模擬已成為研究采空區穩定性的重要手段之一。王曉軍等[12]利用FLAC3D軟件完成多因素組合影響階段礦柱上采過程數值模擬正交試驗，分析了單一影響因素與頂板臨界厚度的關系，利用多元非線性回歸的數學方法，建立了上采過程3因素組合影響下頂板臨界厚度數學預測公式。何標慶[13]利用FLAC3D軟件對福建省某礦區大型采空區群的穩定性進行了模擬，結果表明采空區間柱多發生塑性破壞，采空區上下盤圍巖存在冒落風險。彭超等[14]利用FLAC3D軟件對某大理巖礦山采空區穩定性進行了模擬分析，結果表明采空區塑性破壞主要發生在頂板淺層圍巖，采空區不會發生大規模失穩，并根據不同區域的穩定性制定相應的處理方案。

鑒于采空區穩定性受多因素影響的特點，本文綜合各類巖體分級標準評價指標，能夠反映巖體力學參數且容易量化的影響采空區穩定性因素，采用正交試驗確定研究方案，利用霍克布朗準則，將各方案中的巖體質量指標轉化了巖體力學參數，利用FLAC3D軟件模擬分析影響采空區穩定性各因素的敏感性，對確定采空區穩定性評價的權重及礦山采場結構參數提供參考。

1 采空區穩定性影響因素分析及選取

影響采空區穩定性的因素較多，一般可概括為巖體質量因素、采空區規格參數和誘發因素三類。巖體質量是影響巖體穩定性的最基本因素，目前國際巖體分級標準包括Q分級[15-16]、RMR分級[17-18]、MRMR分級[19-20]以及《工程巖體分級標準》(GB/T 50218—2014)，各分級標準所需的巖體質量因素見表1。不同分級標準的側重點和選擇巖體質量因素不盡相同，因此，本文選定的分析采空區穩定性影響因素能基本反映巖體質量，容易量化，而且通過這些因素可直接或間接估算出巖體的力學參數。點荷載強度或單軸抗壓強度是反映巖體質量的重要指標，是大部分分級標準都不可缺少的，而且也是估算巖體力學參數的基礎，二者具有良好的相關性，考慮到單軸抗壓強度更加直接，因此選擇巖石單軸抗壓強度作為采空區穩定性的分析指標。巖石質量指標RQD、節理間距、巖體完整性系數、節理面產狀、節理面條件等表征結構面特征的因素，存在相關性或是同一參數在不同方面的反映程度，根據上述原則選擇巖石質量指標RQD、節理間距作為采空區穩定性因素進行分析。地下水對巖體工程穩定性和巖體本身強度具有重要影響，因此地下水因素在采空區穩定性分析中是不能忽略的。在已知節理面條件和產狀的條件下，通過選定的上述因素即可獲得巖體的RMR值即反映巖體質量，再利用Hoek-Brown強度準則便可估算出巖體的抗拉強度、內聚力、內摩擦角、彈性模量等力學參數。在模擬計算中還需要泊松比來確定水平應力大小和體積模量等參數，因此最終選擇的影響采空區穩定性巖體質量因素包括單軸抗壓強度、RQD、節理面間距、地下水、泊松比等5個參數。

表1 不同分級標準包含的巖體質量因素Table 1 Rock mass quality factors included in different grading standards

采空區穩定性很大程度上受采空區本身規格參數影響，主要包括采空區的高度、面積、埋藏深度、形狀。生產實踐中形成的采空區形狀較為復雜，很難量化，為了便于分析量化，本文簡化為規則采空區，用采空區的長寬比來定量表征采空區的形狀。因此，在采空區規格參數中選擇采空區的高度、面積、埋深、長寬比作為采空區穩定性評價因素。

實踐表明，眾多采空區災害的發生，多是由于連續強降雨、山體滑坡、大規模爆破振動、采動擾動影響以及相鄰采空區的影響等因素誘發的，可稱為誘發因素，這些因素和采空區本身的穩定性無直接關系，且難于量化，因此本文不予考慮。

2 正交試驗方案及力學參數估算

2.1 正交試驗方案設計及數值模型建立

根據上述分析，本文選取9個因素，分別為單軸抗壓強度、RQD、節理面間距、地下水、泊松比、采空區高度、采空區面積、采空區埋深和采空區的長寬比，并對各因素對空區穩定性影響程度進行分析。根據正交原則設計了“9因素4水平”的正交試驗方案(表2)。利用FLAC3D軟件建立各方案采空區模型，由于后續正交分析中要比較各方案的塑性區體積，為使結果具有可比性，建立模型時盡量使各模型采空區周圍的圍巖網格尺寸和密度保持一致，由于篇幅有限，只列出前4個方案的數值模型，如圖1所示。

表2 正交試驗方案Table 2 Orthogonal test scheme

圖1 前四個方案模型圖Fig.1 The simulation model of the four test schemes

對模型施加邊界條件，模型底部采取鉸支固定邊界法，四周邊界約束其橫向位移，初始垂直應力為自重應力，根據模型尺寸以及方案中采空區的埋深，在模型頂部分別施加1.08 MPa、6.48 MPa、11.87 MPa和17.28 MPa的垂直應力，水平應力根據凈水壓力假設，計算公式見式(1)。

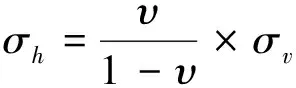
(1)

式中：σh、σv分別為圍巖水平應力和垂直應力；v圍巖泊松比。

本次數值計算將礦巖視作非線性彈塑性介質，采用莫爾-庫倫準則作為屈服準則，其控制方程見式(2)。

(2)

式中：σ1、σ3分別為最大主應力和最小主應力；c、φ分別為材料黏聚力和內摩擦角；F為破壞判斷系數，當F≥0時，材料將發生剪切破壞。

另外，材料在拉應力狀態下，采用抗拉破壞強度準則。其力學模型見式(3)。

F=σt-Rt

(3)

式中：σt為材料所受拉應力；Rt為材料抗拉強度。如果拉應力超過材料抗拉強度(F≥0)，材料將發生拉破壞。

2.2 巖體質量參數量化和力學參數估算

巖體質量參數對采空區穩定性的影響通過對圍巖力學參數反映出來，因此各方案的巖體質量參數估算圍巖的力學參數，不僅可將巖體質量參數量化，還可以為數值模擬采空區穩定性提供基礎。目前，最常用的巖體參數估算方法是經驗公式法，被廣泛采用的方法主要有完整性系數(Kv)修正法、費森科法[21]、格吉法[22]以及霍克-布朗法[23]。 眾多研究[24-25]認為Hoek-Brown強度準則比較全面地反映了巖體結構等特征對巖體強度的影響，是發展最完善的方法。Hoek-Brown巖體破壞準則表達式見式(4)。

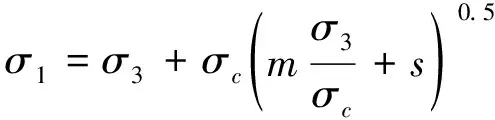
(4)

式中：σ1、σ3分別為巖體破壞時的最大主應力和最小主應力；m為巖體的Hoek-Brown常數；s為巖體材料性質的無量綱系數，m、s可用式(5)和式(6)估算。

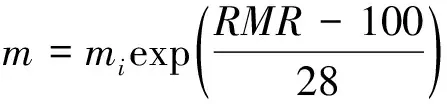
(5)

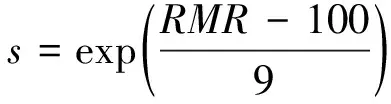
(6)

式中：mi可根據不同類型巖體的Hoek-Brown常數表[20-21]來選取；RMR可根據巖石的強度、RQD值、節理間距以及地下水影響的綜合評價巖體分類指標，其值可通過節理巖體的巖石力學分類(RMR)表計算得出[26-27]。

當σ1=0時，由式(4)可以得到巖體的抗拉強度，見式(7)。

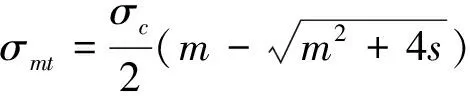
(7)

Hoek-Brown給出巖體彈性模量Em與地質強度指標GSI的關系見式(8)。

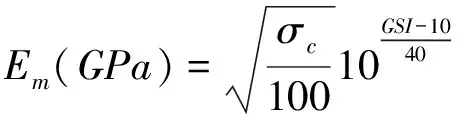
(8)

式(8)可以用巖體分類指標RMR替代GSI值進行彈性模量估算。

Mohr-Coulomb強度準則認為巖體強度主要與巖體的內聚力c和內摩擦角φ有關，而最大主應力和最小主應力σ1、σ3之間存在線性關系，見式(9)。

σ1=σmc+kσ3

(9)

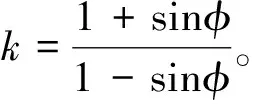
當0<σ3<0.25σc時，所做的三軸實驗結果同時符合Hoek-Brown準則與Mohr-Coulomb準則，可由式(4)確定的不同σ1、σ3對式(9)回歸得到巖體抗壓強度σmc和k。

另外，巖體內摩擦角和內聚力可由式(10)和式(11)求解。

(10)

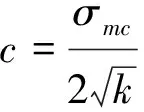
(11)

假設采空區圍巖為石灰巖，節理面稍粗糙，寬度<1 mm，節理面巖石軟弱，根據不同方案的巖體質量數據獲得相應的RMR等相關參數，再利用Hoek-Brown準則便可估算出相應的力學參數，見表3。

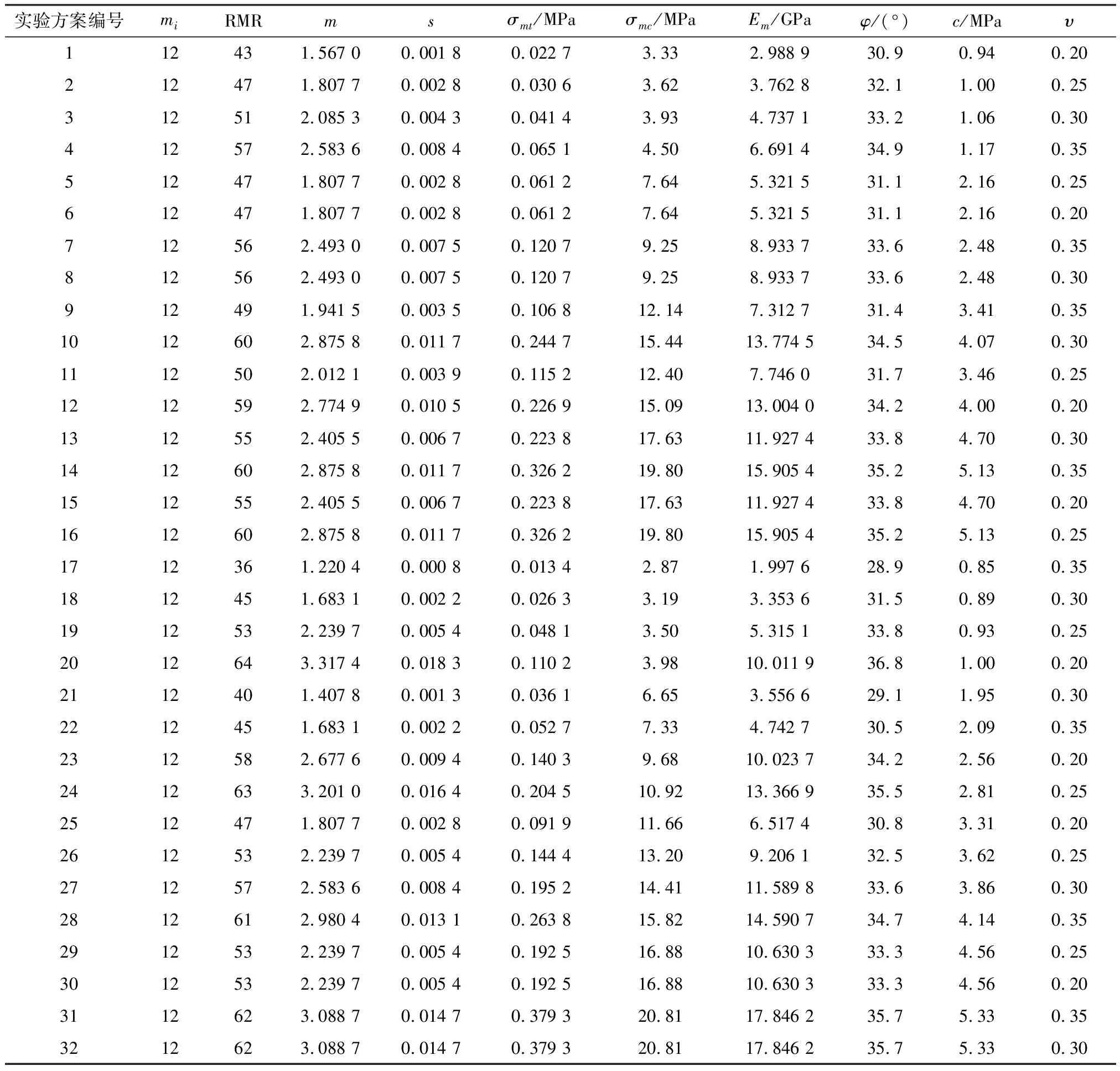
表3 各試驗方案的計算參數Table 3 Parameters of each test scheme

3 模擬結果分析

為了對表1的試驗方案進行評價，需要制定評估指標。采空區圍巖的塑性變形，可表征采空區失穩的開始，塑性區總體積的大小可評估采空區最終的穩定程度。不同采空區參數條件下，采空區頂板和邊壁的塑性變形程度是不同的，有些采空區邊壁巖體不斷片幫導致最終采空區失穩，有些采空區失穩形式是頂板直接冒落，為評估采空區參數和失穩形式關系，頂板塑性區和邊壁巖體塑性區可作為模擬結果的評估指標。因此，選擇采空區塑性區總體積，頂板塑性區體積和邊壁巖體塑性區體積作為各方案評估的指標。利用Fish語言編輯的塑性區體積查詢小程序，可獲得各方案的塑性體積，結果見表4。

對表4中的采空區模擬結果進行極差分析，結果見表5。其中，K1i、K2i和K3i分別為指標采空區頂板塑性區體積、采空區邊壁塑性區體積和采空區圍巖塑性區總體積在水平i下指標的偏差平均值(i=1、 2、 3、 4)，Rj為對應三個指標的極差(j=1、2、3)。

表4 各試驗方案的計算結果Table 4 Statistics of calculation results of each test scheme

通過極差計算得到的采空區頂板塑性區體積的影響因素敏感性主次順序依次為：單軸抗壓強度>采空區埋深>采空區面積>泊松比>涌水量>RQD>節理面間距>采空區長寬比>采空區高度；采空區邊壁塑性區體積的影響因素敏感性主次順序依次為：采空區埋深>采空區長寬比>單軸抗壓強度>采空區高度>采空區面積>RQD>節理面間距>泊松比>涌水量；采空區塑性區總體積的影響因素敏感性主次順序依次為：單軸抗壓強度>采空區埋深>采空區面積>采空區高度>采空區長寬比>泊松比>節理面間距>RQD>涌水量。綜合這3個指標可知，采空區埋深、采空區面積、單軸抗壓強度、長寬比均排在前列，為進一步評估這4個因素隨水平變化對采空區穩定性的影響趨勢，將表5中各指標偏差的平均值，繪制成與對采空區敏感性最為敏感的4個因素、水平的關系趨勢圖，如圖2～圖4所示。各指標的偏差平均值大小與單軸抗壓強度、采空區面積、采空區埋深和采空區長寬比因素水平變化呈曲線變化關系，采空區頂板塑性區體積偏差平均值隨水平變化呈快速降低-緩慢減小或緩慢升高-快速上升的變化關系，邊壁塑性區體積偏差平均值隨水平變化呈先增加后降低的變化關系，圍巖塑性區總體積偏差平均值隨水平先變化近似呈線性增加或降低變化關系。總之，采空區埋深、采空區面積、單軸抗壓強度、長寬比4個因素是對采空區穩定性影響最為敏感的，在評估采空區穩定性和設計礦房尺寸時，應將這4個因素作為重點因素。

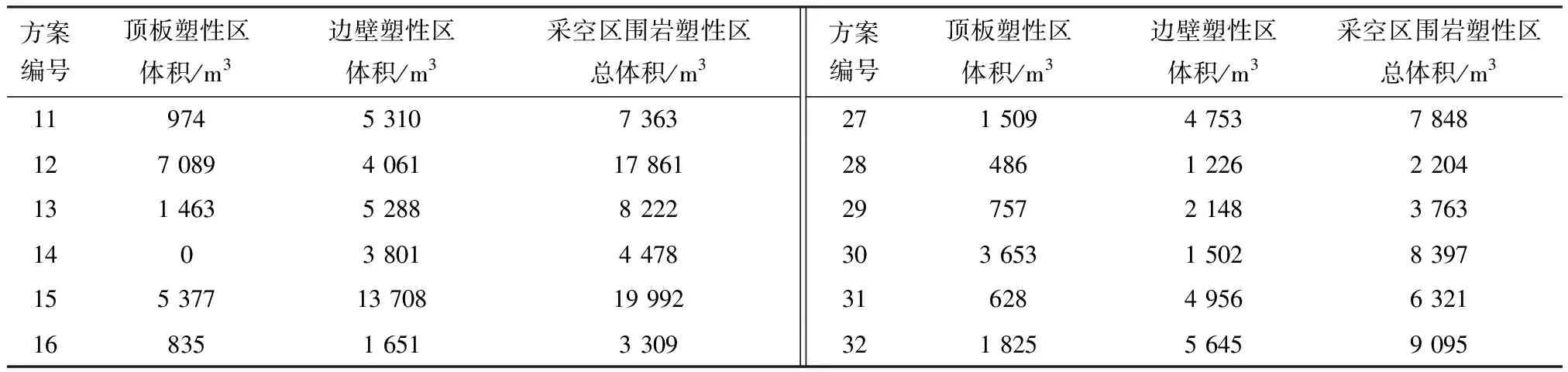
續表4

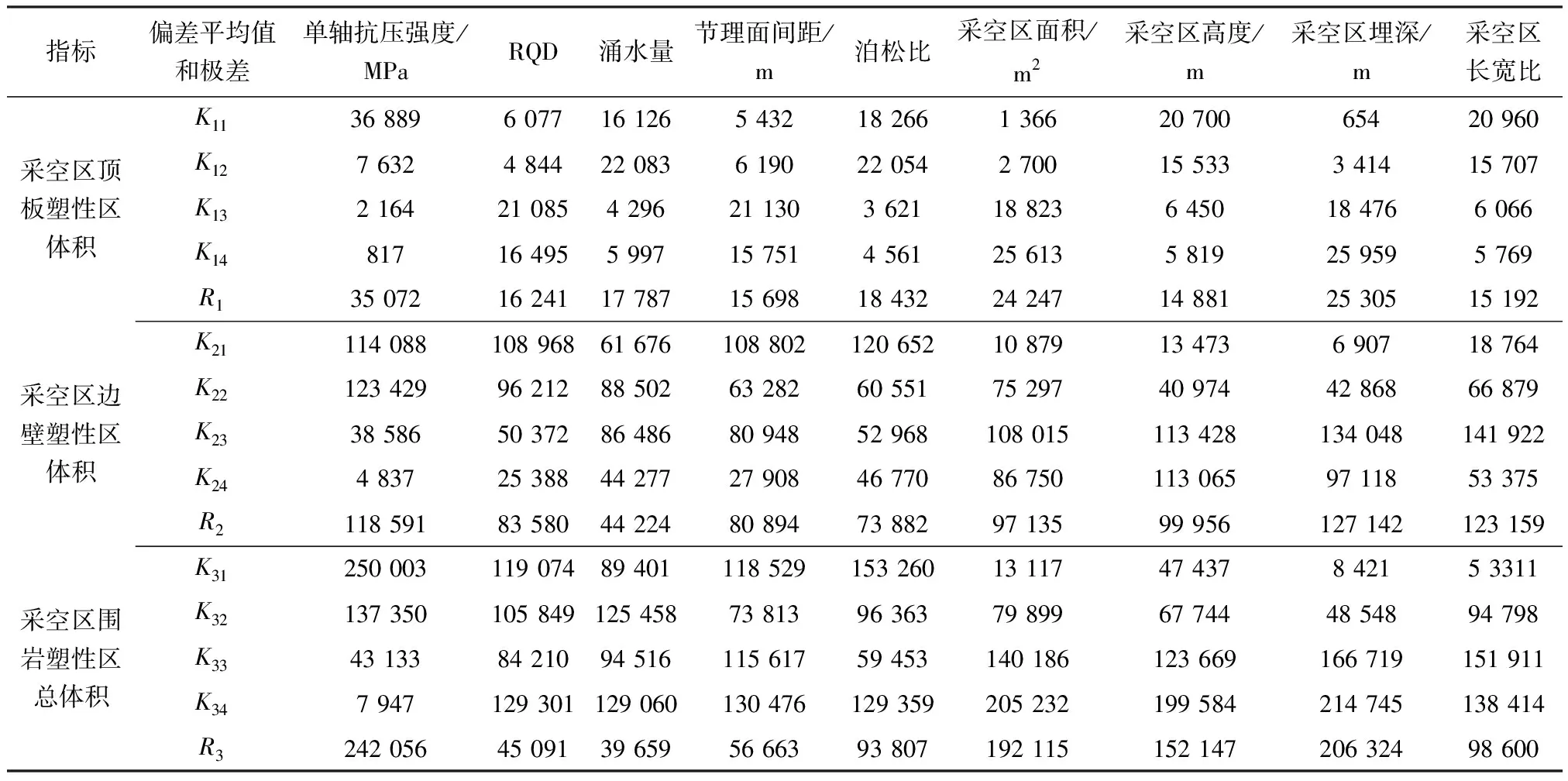
表5 各試驗方案的極差分析Table 5 Extract analysis results of each test scheme

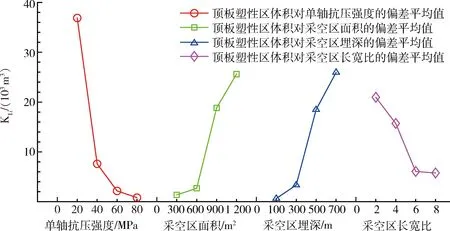
圖2 頂板塑性區指標偏差平均值隨因素和水平的變化趨勢Fig.2 Trend of the deviation average value of volume of roof plastic zone along with factors and levels

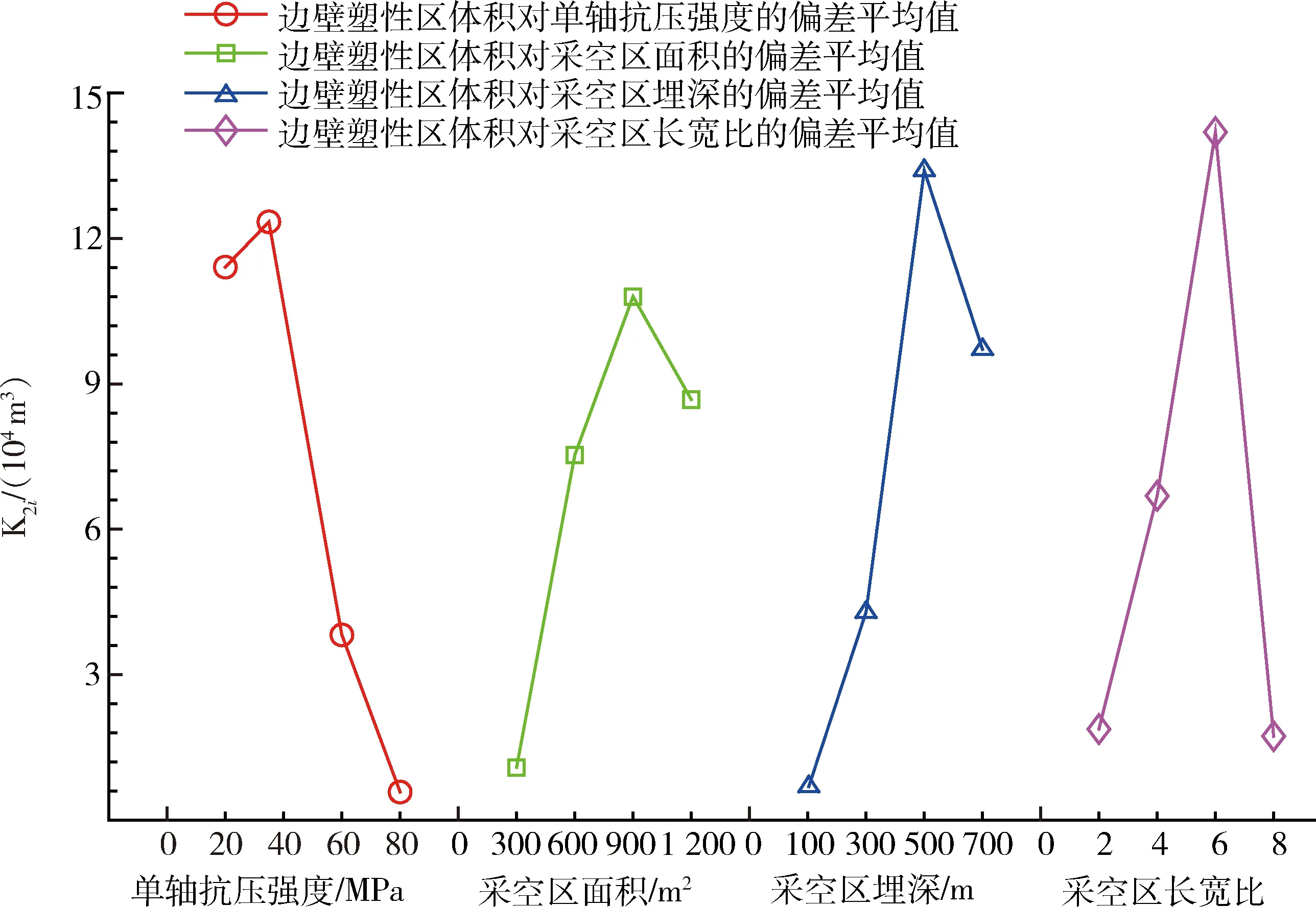
圖3 邊壁塑性區指標偏差平均值隨因素和水平的變化趨勢Fig.3 Trend of the deviation average value of volume of sidewall plastic zone along with factors and levels

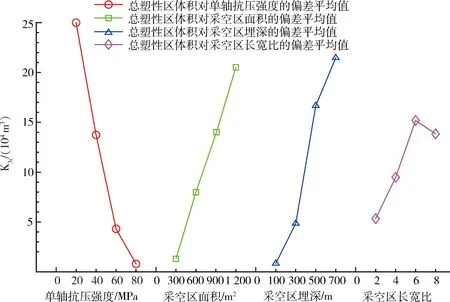
圖4 總塑性區指標偏差平均值隨因素和水平的變化趨勢Fig.4 Trend of the deviation average value of volume of total plastic zone along with factors and levels

4 結 論

1) 在頂板塑性區體積，邊壁塑性區體積和塑性區總體積評估指標下，各因素對采空區穩定性影響的敏感性不盡相同，根據不同指標下的因素敏感性順序，采空區埋深、采空區面積、單軸抗壓強度、長寬比4個因素是對采空區穩定性影響主要因素。

2) 采空區頂板塑性區體積偏差平均值隨水平變化呈快速降低-緩慢減小或緩慢升高-快速上升的變化關系，邊壁塑性區體積偏差平均值隨水平變化呈先增加后降低的變化關系，圍巖塑性區總體積偏差平均值隨水平先變化近似呈線性增加或降低變化關系。

3) 對于具體礦山而言，巖體質量參數已固定，某一采深條件下的采場穩定性主要取決于采空區面積和長寬比，采場結構參數和穩定性也需要根據采深的變化進行動態評估。