Wi-Fi網絡移動邊緣計算資源分配策略研究

沈 冬，方旭明

（西南交通大學，四川 成都 611756）

0 引言

隨著無線通信技術的飛速發展，移動設備的應用種類變得日益豐富，衍生出虛擬現實（Virtual Reality，VR）、增強現實（Augmented Reality，AR）等時延敏感型、計算密集型應用。然而由于受限于體積，移動設備的計算能力、電池能量有限，可能無法及時處理這類應用。此外，該類應用的計算可能會消耗大量能量[1]，從而縮短移動端續航時間或電池壽命。由歐洲電信標準化協會（European Telecommunications Standards Institute，ETSI）提出的移動邊緣計算[2,3]（Mobile Edge Computing，MEC），可以較好地解決上述問題。通過該技術，移動設備可將計算任務卸載到靠近用戶側和位于接入網絡邊緣的MEC服務器，從而減輕移動端的計算負擔，降低任務處理時延與移動端能耗。

如今，由IEEE 802.11系列標準所定義的Wi-Fi已經成為最受歡迎的無線數據傳輸技術之一，有超過一半的用戶數據通過Wi-Fi網絡進行傳輸[4]。最新一代Wi-Fi標準802.11ax已經正式封標，并已投入使用，該標準具有高吞吐量、低時延等特點。Wi-Fi網絡具有大帶寬、低時延、分布廣、無移動運營商資費等特點，且用戶數據僅在局域網內進行傳輸，安全性高，因此相比蜂窩網絡更能滿足移動邊緣計算的需求。

關于移動邊緣計算的相關研究主要集中在MEC網絡架構[5]、計算任務卸載策略[6]、計算任務卸載策略與資源分配聯合優化算法[7]。由于MEC服務器通常需要在資源有限的情況下同時為多個移動設備提供計算服務，因此，計算任務卸載策略與資源分配算法對移動邊緣計算的性能有顯著影響。計算任務卸載與資源分配的聯合優化問題已成為移動邊緣計算的研究熱點之一。

絕大部分文獻基于蜂窩網與車聯網，研究移動邊緣計算下的計算任務卸載與資源分配聯合優化問題。在文獻[8]中，作者將數據壓縮技術引入多用戶單服務器MEC系統，在滿足時延限制的條件下，通過聯合優化卸載策略、資源分配和數據壓縮比例以降低移動端能耗。文獻[9]針對提供內容緩存服務的MEC系統，提出了內容緩存決策、卸載決策、資源分配聯合優化問題，并通過將用戶請求的內容緩存到MEC服務器的方式，避免相同內容的重復傳輸，降低回傳鏈路的帶寬占用與任務處理時延。針對車聯網中由于車輛移動導致的任務卸載失敗的問題，文獻[10]考慮車速等限制條件，提出了動態卸載策略，即通過將任務分成多個子任務并卸載到不同基站的服務器進行并行計算的方式，實現在任務卸載不中斷的前提下，最小化每個基站的任務處理時延。文獻[11]提出了一種啟發式算法，以優化所有移動端的最大任務處理時延，從而提高了用戶公平性。文獻[12]針對多用戶多服務器的MEC系統，提出了基于強化學習的分布式任務卸載策略，以實現服務器的計算負載均衡。

針對Wi-Fi網絡移動邊緣計算下的計算任務卸載與資源分配的研究數量較少，且相關文獻的研究場景主要是基于蜂窩與Wi-Fi的異構網絡，并通常對資源分配模型進行了簡化，或不滿足Wi-Fi網絡資源分配的限制條件，因此所提資源分配算法不適用于802.11ax Wi-Fi網絡。文獻[13]在基于蜂窩與Wi-Fi的異構網絡下研究單用戶任務卸載問題，通過基于深度強化學習的算法以優化任務卸載長期開銷，實現任務處理時延、排隊時延、成本的折中。文獻[14]以最小化移動端時延開銷為優化目標，研究了基于Wi-Fi網絡MEC架構下的聯合任務卸載與資源分配問題；然而該文獻僅簡單地考慮傳輸速率與服務器負載強度和服務用戶數量成反比，并沒有給出具體的資源分配模型。文獻[15]的作者將能量捕獲技術引入MEC系統，研究由基于非正交多址（Non-Orthogonal Multiple Access，NOMA）技術的蜂窩與基于正交頻分多址（Orthogonal Frequency Division Multiple Access，OFDMA）技術的Wi-Fi組成的異構網絡下的任務卸載與資源分配問題；然而該文獻在Wi-Fi網絡下采用的頻譜資源粒度為子載波，因此該文獻所提資源分配算法并不適用于頻譜資源粒度為資源單元（Resource Unit，RU）的802.11ax Wi-Fi網絡。文獻[16]提出了一種基于802.11ac Wi-Fi網絡的多接入點（Access Point，AP）多用戶MEC架構，并基于此架構研究任務卸載與資源分配聯合優化問題，通過分支限界法求解以最小化移動端能耗；然而作者在仿真時采用了固定調制與編碼方式（Modulation and Coding Scheme，MCS），且忽略了通信資源分配對傳輸速率的影響。文獻[17]研究了基于Wi-Fi與蜂窩異構網絡下的任務卸載問題，并提出了基于交替優化與線性規劃的優化算法，以降低時延與能耗的加權；然而該文獻沒有對通信與計算資源分配進行優化，且采用的Wi-Fi網絡為802.11ax之前版本的傳統Wi-Fi網絡，因此并不涉及802.11ax Wi-Fi網絡下的OFDMA資源分配問題。

綜上所述，目前鮮有基于Wi-Fi網絡的移動邊緣計算解決方案，且現有文獻在研究資源分配問題時，采用的頻譜資源粒度通常為按任意比例分配的帶寬、按任意數量分配的子載波或者是大小固定、規格單一的子信道，并且將香農容量等效為實際的傳輸速率。而最新一代802.11ax Wi-Fi網絡的頻譜資源可被分為多種不同固定規格的RU，并且實際的傳輸速率取決于RU規格和MCS，因此現有文獻所提資源分配算法并不適用于Wi-Fi網絡。

針對上述問題，本文基于802.11ax Wi-Fi網絡，對移動邊緣計算下的計算任務卸載與資源分配問題進行了研究，主要貢獻如下：

（1）給出了基于802.11ax Wi-Fi網絡的計算任務整體卸載與資源分配系統模型；

（2）考慮任務時延限制，建立了卸載決策與資源分配聯合優化問題，最小化移動設備的任務處理總能耗；

（3）提出了基于坐標下降法與任務優先級的卸載與資源分配方案，所提方案具有較低算法復雜度，且滿足802.11ax Wi-Fi網絡的資源分配限制條件；

（4）通過仿真驗證了所提方案能夠在顯著降低移動設備任務處理總能耗的同時，提高QoS滿意率，有效提高了基于Wi-Fi網絡的MEC性能。

1 系統模型與問題建模

假設在一個由單AP、多站點（Station，STA）組成的802.11ax Wi-Fi網絡中，AP含MEC服務器，具有通信、存儲和一定的計算能力，如圖1所示。AP和STA均是802.11ax設備，且工作在5 GHz頻段。

記STA集合為M={1,2,…,M}，STAm的計算任務為Tm=(dm,cm,τm)，其中，dm為任務數據量大小，單位為比特；cm為任務所需的CPU計算量大小，單位為時鐘周期（cycle）；τm為任務的時延限制，單位為秒。假設STA的計算任務無法進一步分割，STA只能對任務進行本地計算或者整體卸載。假設AP與STA的CPU在每個時鐘周期所能處理的指令數相同，即具有相同的每周期完成的指令數（Instructions Per Cycle，IPC），則AP與STA的計算能力僅與CPU頻率有關。假設同一個任務在本地進行計算以及在服務器進行計算所需要的CPU計算量相同。由于本文設計的方案僅針對計算任務，故假設系統內此時沒有通信業務，因此僅考慮計算任務的傳輸，不考慮計算任務與通信業務的混合傳輸。

1.1 本地計算模型

當STAm進行本地計算時，記STAm的本地計算資源為，則本地計算時延和能耗可以分別表示為：

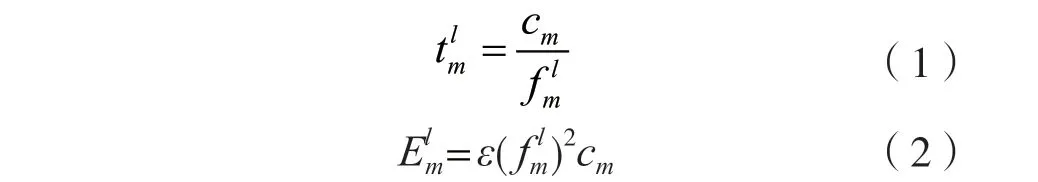
式中：ε為能耗系數[18]。

1.2 卸載計算模型

當STAm進行卸載計算時，STA首先需要將任務數據上傳給AP，其次由AP的MEC服務器對任務進行計算，最后AP將任務計算結果回傳給STA。

在802.11ax Wi-Fi網絡中，頻譜資源的最小粒度為RU，且每個STA只能使用1個RU。RU規格是離散的，且種類有限，以80 MHz帶寬為例，按照包含子載波個數由少到多，可將RU分為26-tone、52-tone、106-tone、242-tone、484-tone、996-tone RU。為了方便，將RU表示為其占用子載波的數量，則26-tone、52-tone、106-tone、242-tone、484-tone、996-tone RU可以分別表示為26，52，106，242，484，996。

STAm的上行傳輸速率可以表示為：

式中：pm為STAm的傳輸功率；gm為STAm到AP的信道增益；RUm為STAm所用RU的規格，記為其所包含的子載波數量；SINRm為AP在STAm所用RU上的信干噪比；V(RUm,MCS(SINRm))為在規格為RUm的RU上，接收端的信干噪比為SINRm時，所能達到的最大MCS所對應的傳輸速率；N0為噪聲功率譜密度；bc為單個子載波占用的帶寬。

RU規格越大，則帶寬越大，而采用更高階的MCS可以提高單個符號所攜帶的比特數，并且降低前向糾錯的編碼開銷，因此傳輸速率與RU規格和MCS成正相關。MCS的種類有限，且與SINR有關，SINR越大，則可以采用更高級別的MCS。本文將802.11ax協議所定義的接收機最小輸入靈敏度減去噪聲功率，以獲取SINR與MCS的映射關系。此外，通過查詢802.11ax協議的方式以獲取給定RU規格和MCS所對應的傳輸速率。

一般而言，任務計算結果比任務數據小很多[19]，因此忽略下行傳輸過程帶來的時延和能耗，則STAm的傳輸時延和傳輸能耗可以分別表示為：

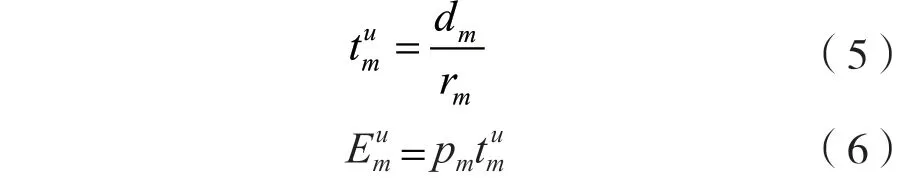
記AP為STAm分配的服務器計算資源為fms，則STAm的任務在服務器計算的時延可以表示為：

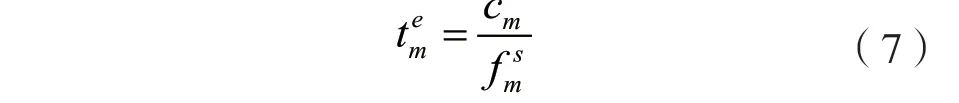
STAm的卸載計算時延和能耗可以分別表示為：

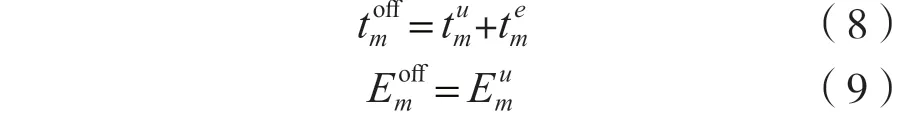
1.3 問題建模

記卸載決策向量為X={x1,x2,…,xM}，RU分配向量為RU={RU1,RU2,…,RUM}，傳輸功率分配向量為P={p1,p2,…,pM}，本地計算資源分配向量為，服務器計算資源分配向量為。本文在滿足任務時延限制的條件下最小化STA的任務處理總能耗，則優化問題可以表示為：

式中：xm=0為本地計算；xm=1為卸載計算；RUmax為AP所能提供的最大RU規格；F s為服務器的最大計算資源；為STAm的最大本地計算資源；為STAm的最大傳輸功率。

2 任務卸載與資源分配方案

在優化問題P中，整形變量的存在導致該問題是一個混合整數非線性規劃問題，且待優化變量較多，難以通過優化理論直接求得最優解。因此，本文將原始優化問題拆分為卸載決策子問題與資源分配子問題進行求解，通過在給定卸載策略的情況下求解資源分配子問題，并對卸載策略進行迭代優化以求得次優解。

2.1 資源分配子問題

在給定卸載策略的情況下，原始優化問題可轉化為本地計算資源分配問題P1與卸載計算資源分配問題P2的次優化問題，分別如式（11）、式（12）所示。

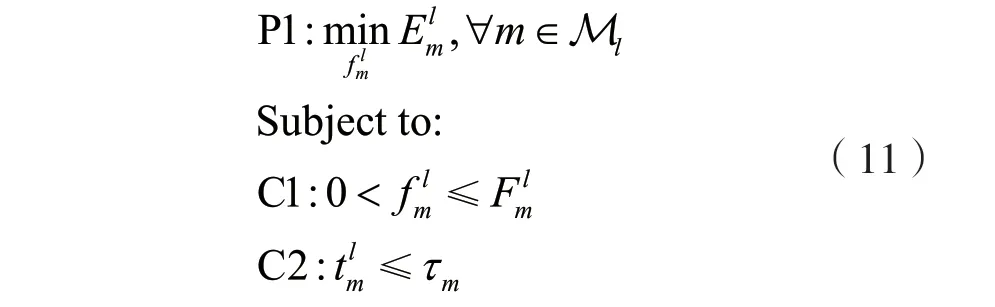
式中：Ml為進行本地計算的STA集合。優化問題P1為在滿足任務時延限制的條件下，最小化每個進行本地計算的STA的能耗。

式中：Moff為進行卸載計算的STA集合。優化問題P2為在滿足任務時延限制的條件下，最小化所有進行任務卸載的STA的能耗之和。

由于每個STA的信道質量、任務數據量、任務計算量、任務時延限制不同，因此當卸載策略確定后，均分帶寬資源、服務器計算資源的方式無法保證較好的性能，需要通過合理的通信資源與計算資源分配，以在盡量滿足任務時延限制的條件下，降低STA的任務處理總能耗。為此，本文綜合考慮Wi-Fi網絡的資源分配特點與限制條件，提出了一種基于任務優先級的資源分配算法（Task Priority Based Resource Allocation，TPBRA），流程如圖2所示。

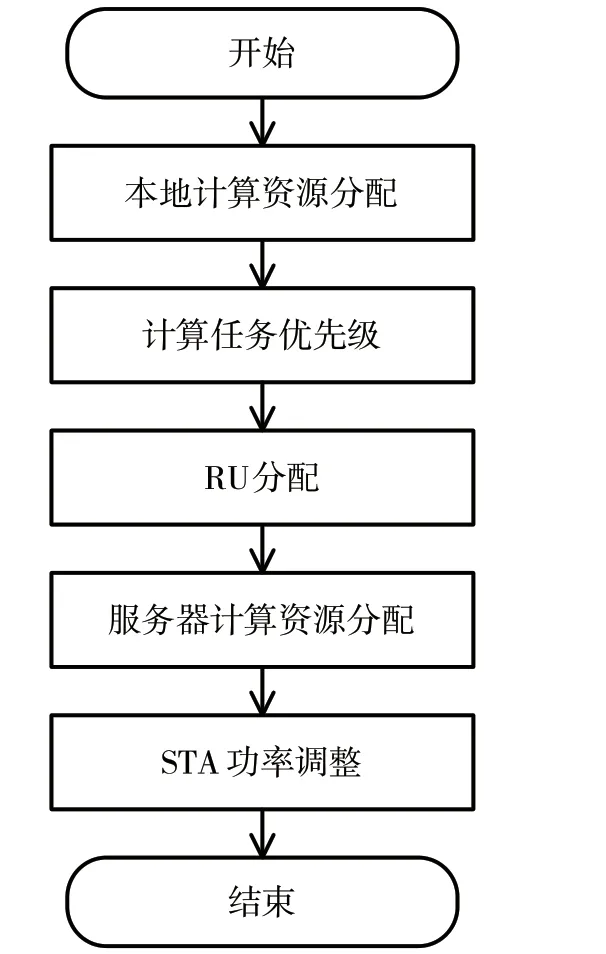
圖2 基于任務優先級的資源分配算法流程

基于任務優先級的資源分配算法流程具體如下文所述。

（1）本地計算資源分配。若STA進行本地計算，則AP無須為STA分配通信資源和服務器計算資源。由于移動設備可通過動態電壓調整（Dynamic Voltage Scaling，DVS）技術對本地計算資源進行調整，從而降低能耗[20]。因此在任務時延限制的條件下，STA的最佳本地計算資源可以表示為：

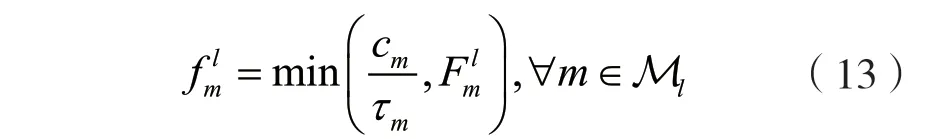
（2）計算任務優先級。對于進行任務卸載的STAm而言，根據STA所需最小服務器計算資源、所需最小傳輸速率、傳輸能力capacitym計算STA任務優先級wm，表達式分別為：

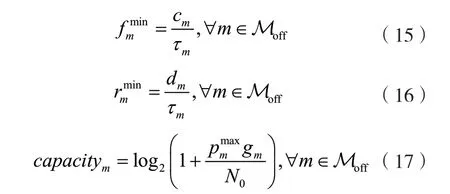
式中：αj(j∈{1,2,3})為優先級系數，且。對于任務數據量越大、任務計算量越大、任務時延限制越苛刻、信道質量越差、最大傳輸功率越小的STA而言，其任務的時延限制條件越不容易被滿足，因此為其設置更大的任務優先級，并在后續進行通信與計算資源分配時，為任務優先級更大的STA分配更多資源。

（3）RU分配。在802.11ax Wi-Fi網絡中，RU規格是離散的，其種類有限，且一個STA最多只能使用一個RU，因此本文將RU分配問題建模為RU規格與STA任務優先級的匹配問題。假設進行卸載的STA數為Moff，且將整個帶寬拆分為Moff個RU的RU規格組合共有K種，則RU分配問題可以看作從K種RU規格組合中選取一種最合適的RU規格組合，并且為這Moff個RU與STA確定一一對應的關系。

記第k種（k∈{1,2,…,K}）組合下各個RU的規格之比（由大到小排序）為s1,k:s2,k:…:sMoff,k。對STA按任務優先級由大到小的順序進行排序，得到排序后的STA編號n1,n2,…,nMoff∈Moff。將排序后的STA任務優先級之比歸一化為其中，然后將K種RU規格組合的RU規格之比歸一化為，其中，

本文將RU規格匹配問題建模為最小化多維空間中兩點距離問題進行求解。設最合適的RU規格組合為第k*種RU規格組合，則k*為：

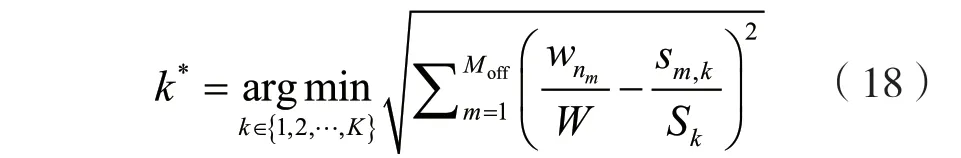
由于在盡量用完帶寬的前提下可用的RU規格組合數較少，因此本文使用窮舉法找到最合適的RU規格組合，最后通過式（19）得到每個參與卸載計算的STA所用的RU規格。

（4）服務器計算資源分配。由于服務器計算資源分配向量F s不會對移動端能耗的大小產生影響，因此本文將服務器計算資源按照任務優先級之比進行分配，如式（20）所示。任務優先級越大，說明該STA的任務時延限制越不容易被滿足，因此需要分給該STA更多的服務器計算資源。

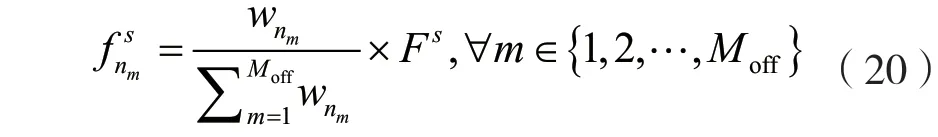
（5）STA功率調整。在完成上述步驟后，資源分配子問題可轉化為Moff個獨立的STA功率優化問題，其表達式為：

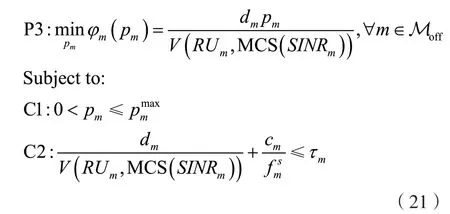
由于傳輸速率V與MCS呈一一對應的離散映射關系，因此難以給出目標函數φm與自變量pm的函數表達式。為了便于分析傳輸功率pm對能耗φm的影響，將傳輸速率V替換為香農容量，則可以得到式（22）所示的優化問題。

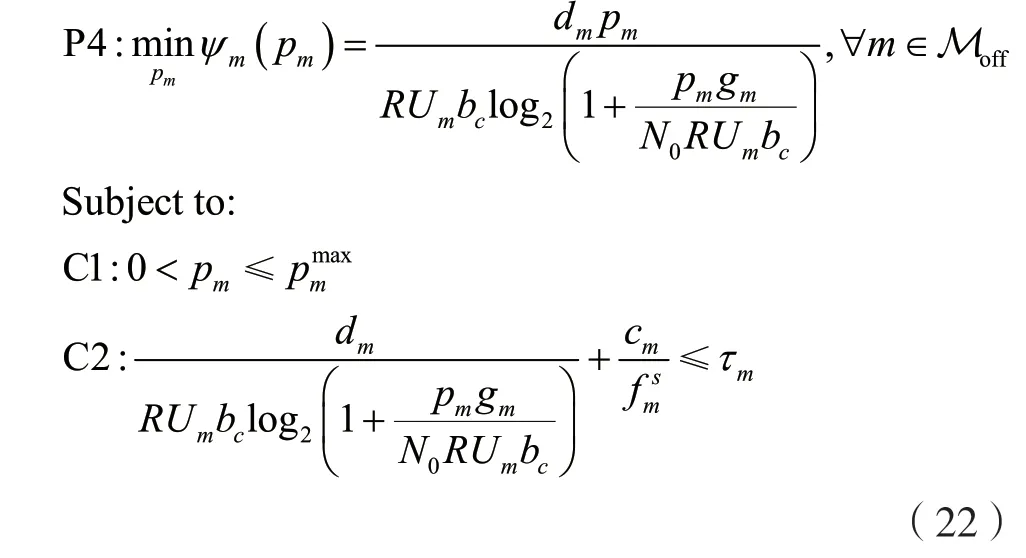
通過進一步求導分析不難得出(pm)>0，故ψm(pm)單調遞增。由于實際的傳輸速率與香農容量成正相關，因此可近似認為能耗隨著功率的增加而增大，故為了最小化STA能耗，需要在滿足任務時延限制C2和STA功率限制C1的條件下盡可能降低傳輸功率。根據上述結論，本文提出了如算法1所示的STA功率調整算法。

2.2 卸載決策子問題

坐標下降法（Coordinate Descent，CD）是一種簡單、高效的迭代優化算法，通過將一個高維的優化問題分解為若干個一維的優化問題，從而極大降低了問題的復雜度。與梯度下降法按照梯度方向搜索目標函數最優值不同，坐標下降法在每次迭代過程中按給定順序依次在每個坐標維度上搜索目標函數的最優值[21]。考慮到卸載策略為0-1變量，因此，對卸載策略向量的每個坐標維度進行搜索時，具有較低的復雜度，故本文基于坐標下降法對卸載策略進行迭代優化。卸載決策流程如圖3所示。

圖3 基于坐標下降法的整體卸載決策流程

基于坐標下降法的整體卸載決策流程具體如下文所述。

（1）確定初始卸載策略。首先預估STA按照最大本地計算資源對任務進行計算是否能滿足時延限制，若否，則STA需要將其任務卸載到MEC服務器。根據式（23）、式（24）確定初始卸載策略。

（2）通信與計算資源分配。按照如圖2所示的TPBRA算法進行資源分配。

（3）卸載策略迭代優化。記STA集合為M={1,2,…,M}，卸載策略優化順序向量為O={o1,o2,…,ok,…,oM}，?ok∈M，第k個被優化卸載策略的STA編號為ok。為了盡量滿足STA的時延限制，本文在計算改變STA卸載策略所帶來的系統增益時，同時考慮STA能耗降低收益和任務如果超時而導致的懲罰。在給定卸載決策向量X時，記RU(X)，P(X)，F l(X)，F s(X)分別為通過基于任務優先級的資源分配算法所得到的RU、傳輸功率、本地計算資源、服務器計算資源分配向量，則在給定卸載策略向量X與資源分配向量RU(X)，P(X)，F l(X)，F s(X)時，考慮超時懲罰后的能耗總開銷Call(X)，它可以表示為：

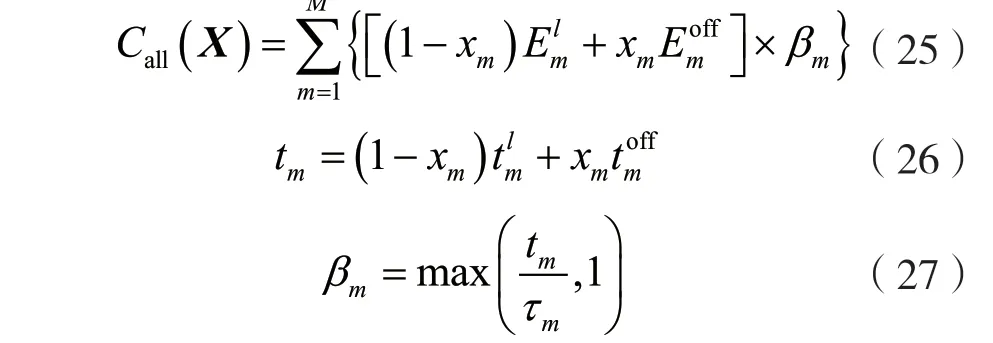
式中：βm為懲罰因子，當STAm的任務處理時延不滿足時延限制時，βm>1，STAm的能耗開銷會進一步增大。通過引入懲罰因子，使得算法在迭代過程中盡量避開不滿足時延限制的卸載策略，從而盡可能保證STA任務時延限制。

式中：⊕表示模2加運算符。

對于每次迭代過程而言，按照給定順序O依次對每個STA的卸載策略進行優化，每個已被優化的STA卸載策略都將作為已知量，用于后續的優化過程。對于單個STA的卸載策略優化而言，首先嘗試改變該STA的卸載策略，并重新進行資源分配，判斷改變該STA卸載策略是否能降低能耗總開銷。若可以，則需要改變該STA的卸載策略，否則該STA的卸載策略保持不變。因此可以表示為：

記第i次迭代所帶來的系統增益為Gi，則Gi可以表示為：

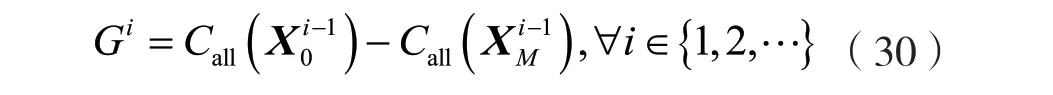
對于第i次迭代，若Gi>0，則本次迭代能夠帶來系統增益，因此本次迭代對卸載策略與資源分配結果的調整有效；若Gi≤0，則本次迭代無法帶來增益，因此本次迭代對卸載策略與資源分配結果的調整無效。則經過第i次迭代后得到的卸載策略向量可以表示為：

由于坐標下降法依次沿著單個變量方向對目標函數進行優化，因此在有限迭代次數內目標函數能夠收斂到一個局部最優解，故本文將算法收斂停止條件設置為Gi≤0。

基于坐標下降法的卸載策略（Coordinate Descent Based Offloading，CDBO）如算法2所示。

3 仿真結果與分析

3.1 仿真場景與參數設置

仿真場景為單AP多STA場景，STA隨機分布在AP周圍。假設需要卸載的任務數據量小于或等于AP所能提供的最大RU剩余承載能力，任務時延限制設置為任務在本地計算最小時延的50%～120%。除非特別聲明，其他仿真參數如表1所示。

表1 仿真參數

為了驗證本文所提方案的有效性，本文通過MATLAB對所提方案和以下3種基線方案的性能進行仿真。

（1）基線1（local-only）：所有任務進行本地計算，并在保證任務時延限制的前提下盡可能降低本地計算資源。

（2）基線2（offload-only+RRA）：所有任務進行卸載計算，并采用隨機資源分配算法，即AP在保證帶寬盡量用完的前提下，為STA隨機分配RU、均分服務器計算資源，且STA采用最大傳輸功率。

（3）基線3（offload-only+TPBRA）：所有任務進行卸載計算，并采用基于任務優先級的資源分配算法。

（4）本文所提方案（CDBO+TPBRA）：采用基于坐標下降法與任務優先級的卸載與資源分配方案。

通過多次實驗并對性能指標取平均值的方式得到仿真結果，性能指標包括了STA的任務處理總能耗、QoS滿意率。其中，QoS滿意率定義為任務處理時延小于或等于任務時延限制的任務數占總任務數的比例。

3.2 性能分析

3.2.1 改變STA數量

圖4和圖5分別為STA任務處理總能耗、QoS滿意率與STA數量的關系。其中，服務器最大計算資源為12 GHz。

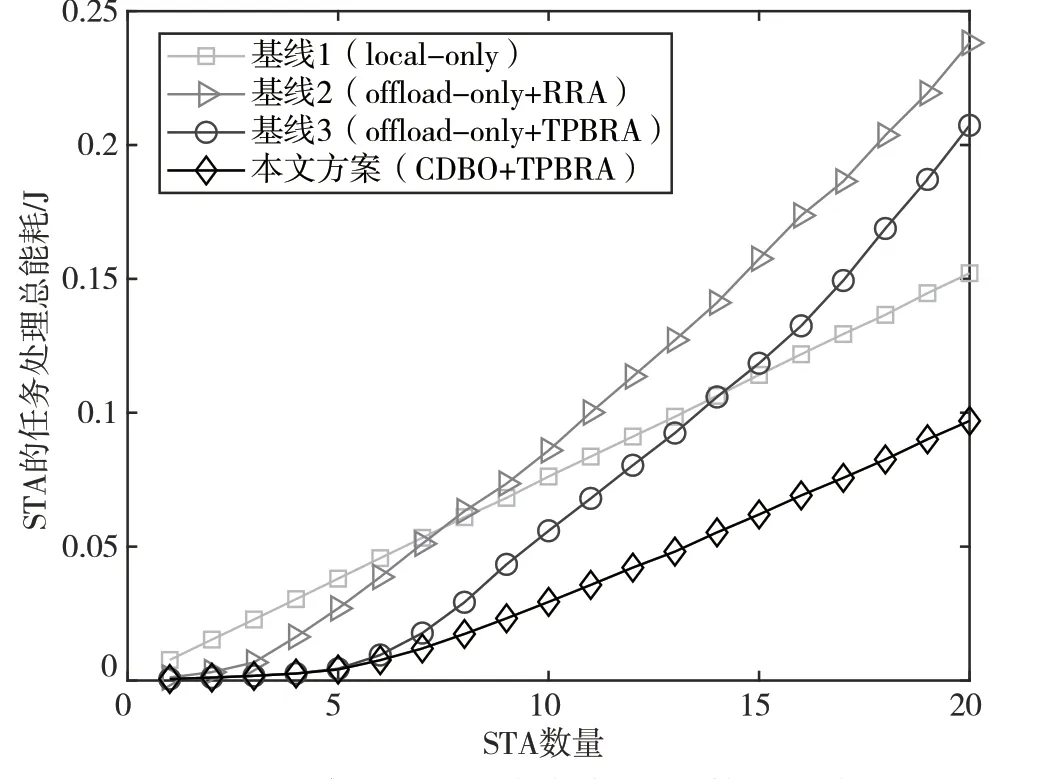
圖4 STA的任務處理總能耗與STA數量的關系

圖5 QoS滿意率與STA數量的關系

從圖4可以看出，本文所提方案的STA任務處理總能耗顯著低于其他方案，且本文所提基于任務優先級的資源分配算法能夠有效降低STA的任務處理總能耗。當STA數量較少時，本文方案的性能曲線與基線3重合，這是因為當STA數量較少時，通信與服務器計算資源是充足的，AP能夠較好地滿足所有STA的任務計算需求，此時本文所提方案會讓所有STA將任務卸載到AP進行計算。

從圖5可以看出，本文所提方案的QoS滿意率顯著高于其他方案，且本文所提基于任務優先級的資源分配算法能夠在通信、服務器計算資源較為充足的情況下適量提高QoS滿意率。當STA數量較少時，由于通信資源與服務器計算資源是充足的，此時全部卸載計算，本文所提方案均能較好地滿足STA的任務時延限制。隨著STA數量逐漸增多，全部卸載計算的QoS滿意率急劇下降，且當STA數增加到一定程度時，全部卸載計算已經無法滿足任何STA的任務時延限制。

綜合圖4與圖5可以看出，當STA數量較少時，由于STA能夠獲取足夠的通信與服務器計算資源，因此全部卸載計算與隨機資源分配也能夠獲得與本文方案較為接近的MEC性能；而當STA數量較多時，由于STA難以獲取足夠的通信與服務器計算資源，因此全部卸載計算與隨機資源分配的MEC性能急劇下降。本文所提方案的MEC性能隨STA數的增加下降較為緩慢，且即使在STA數較大時依然能夠保持不錯的MEC性能。可見本文提出的方案能夠適應不同STA數量，即能夠同時在資源受限與不受限時進行合理的卸載決策與資源分配，實現在盡可能滿足STA任務時延限制的條件下，降低STA任務處理總能耗的功能。

3.2.2 改變任務數據量大小

圖6和圖7分別為STA任務處理總能耗、QoS滿意率與STA任務數據量的關系。其中，STA數量為6，服務器最大計算資源為12 GHz。

圖6 STA的任務處理總能耗與STA任務數據量的關系

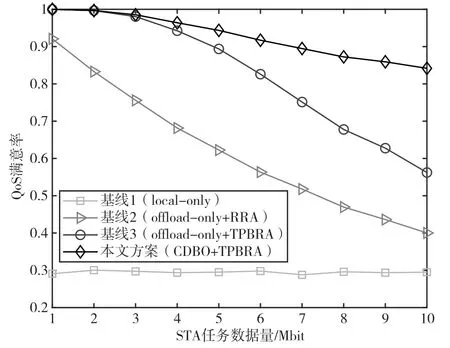
圖7 QoS滿意率與STA任務數據量的關系

從圖6可以看出，本文所提方案的STA任務處理總能耗顯著低于其他方案，且能耗上升速率也遠低于全部卸載計算與隨機資源分配。

從圖7可以看出，除全部本地計算外，其他方案的QoS滿意率均隨著任務數據量的增加而降低。此外，本文所提方案具有最高的QoS滿意率，且QoS滿意率的下降速率也遠低于全部卸載計算與隨機資源分配。

綜合圖6與圖7可以看出，當任務數據量較小時，將所有任務卸載到服務器進行計算以及進行隨機資源分配，也能夠獲得較好的MEC性能；當任務數據量較大時，全部卸載計算與隨機資源分配的MEC性能顯著下降，而本文所提方案的性能下降不明顯，即使在任務數據量較大時仍然能保持較好的MEC性能。這是因為本文所提方案綜合考慮STA計算能力、AP計算能力、任務屬性等參數進行合理的卸載決策，通過將時延限制較為苛刻、數據量較小、計算量較大的任務卸載到AP進行計算，而對時延限制較為寬松、數據量較大、計算量較小的任務在本地進行計算，以充分利用參數的多樣性，使得STA的計算任務與任務計算方式相匹配。此外，本文所提方案在進行資源分配時，為任務時延限制更苛刻、任務數據量更大、任務計算量更大、傳輸能力更差的STA分配更大的RU和服務器計算資源，因此能夠更好地滿足STA的任務時延 限制。

3.2.3 算法復雜度與算法收斂性

圖8為本文所提方案達到收斂所需算法平均迭代次數與STA數量的關系，其中，服務器最大計算資源為12 GHz。可以看出，當STA數量較多時，本文所提方案達到收斂所需算法平均迭代次數依然較小，且迭代次數隨STA數的增加近似呈現線性增長趨勢。

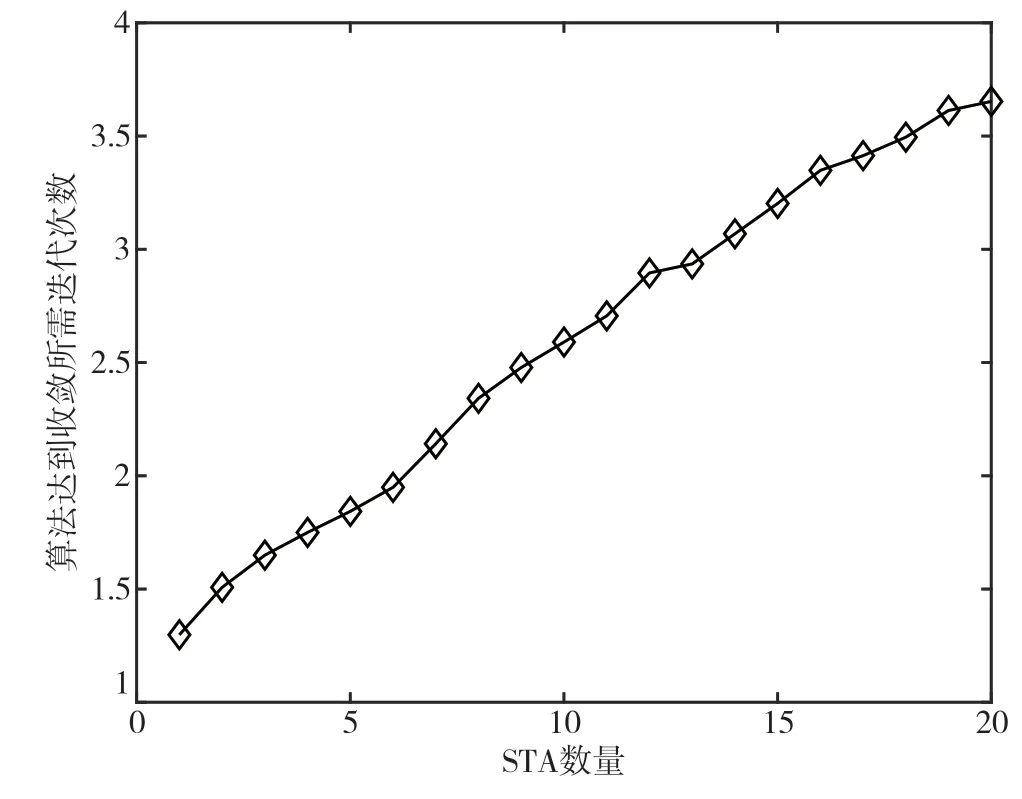
圖8 本文所提方案的算法平均迭代次數與STA數量的關系

圖9為本文所提方案在不同帶寬設置下的收斂性，其中，服務器最大計算資源為24 GHz，STA數量為8，STA任務數據量大小為6 Mbit。可以看出，隨著帶寬的增大，STA的平均傳輸時延降低，因此STA的任務處理總能耗也跟著降低。此外，本文所提方案的STA任務處理總能耗在不同帶寬下均隨著迭代次數的增加而呈現下降趨勢，且均能在一定迭代次數之后收斂到一個固定值，因此本文所提方案具有較好的收斂性。

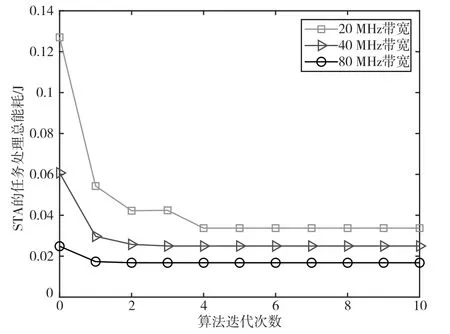
圖9 本文所提方案的收斂性

綜上所述，本文所提方案能夠在不同場景參數下，降低STA任務處理總能耗，提高QoS滿意率，同時具有較低的算法復雜度和較好的收斂性。

4 結語

本文基于802.11ax Wi-Fi網絡，對MEC計算任務卸載與資源分配問題進行了研究。首先給出了任務整體卸載與資源分配系統模型，其次建立了在時延限制條件下最小化移動終端任務處理總能耗的優化問題，再次設計了基于坐標下降法與任務優先級的任務卸載與資源分配方案，最后通過MATLAB對所提方案的性能進行了仿真。仿真結果表明，本文所提出的方案能夠在顯著降低移動端任務處理總能耗的同時，提高QoS滿意率，有效提高了基于Wi-Fi網絡的MEC性能。此外，本文所提方案即使在STA數較多時也能很快收斂，且算法迭代次數隨STA數的增加近似呈線性增長趨勢，因此方案本身的執行開銷不會對MEC性能造成太大負面影響，可見本文方案在實際的Wi-Fi網絡中具有較低的算法復雜度與較高的可行性。