基于瞬時特征參數的調制識別方法

劉 生，于萬里，王勤民

（1.中原工學院，河南 鄭州 450007；2.河南工程學院，河南 鄭州 451191）

0 引言

數字通信信號的調制識別是電子戰場目標信息獲取與態勢分析的重要環節，也是非協作解調的關鍵步驟和基礎。調制識別技術已經廣泛應用在通信對抗、軍事偵察、電磁頻譜管理等方面，在工程應用中，仍是研究的重點[1]。

目前針對通信信號的調制識別方法，主要有基于統計模式識別[2]、小波變換[3]和決策理論[2]等方法，每一種調制信號識別方法都各有特點。文獻[2]從特征參數提取角度改進了傳統決策理論算法，并利用決策樹對信號調制進行識別；文獻[3]通過分析小波的時頻圖區分信號，發現高信噪比小波效果較好，但低信噪比識別效果較差；文獻[4]則從識別方法上進行了創新，首次提出使用神經網絡對通信信號進行識別，雖然識別效果較好，但算法設計復雜且不便工程應用。隨著通信技術的發展，越來越多的算法被應用到實際的工程中。但在調制識別領域，復雜的算法還不能有效地被應用到工程中。因此，研究適合工程實現的自動調制識別算法有著很強的現實需求。

本文將瞬時幅度的譜密度最大值γmax、瞬時相位絕對值的標準偏差σap、瞬時頻率絕對值的標準差σaf與3層全連接神經網絡分類器（Three-layer Fully Connected Neural Network Classifier，TFCNNC）相結合，識別通信信號的調制類方式[5]。使用TFCNNC有效地避免了人為設置門限帶來的誤差。選用瞬時特征參數作為TFCNNC的輸入特征，識別調制方式，并通過仿真得出實驗結果，結果表明該方法不僅性能優于決策樹算法，且設計簡單，復雜度遠低于其他深度神經網絡，便于工程應用。

1 信號模型

在通信過程中，接收信號模型表示為：

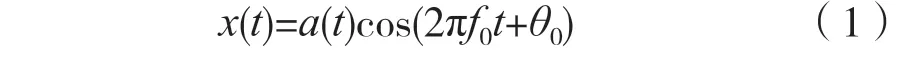
式中：a(t)為信號的瞬時幅度；f0為載頻；θ0為載波相位。

對x(t)進行希爾伯特變換（Hilbert），則可得到其正交分量v(t)，這樣就得到了解析信號z(t)，即可得到通信信號的幅度、相位、頻率等瞬時參數[6]。x(t)的解析信號為：

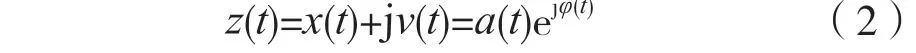
v(t)的計算公式為：

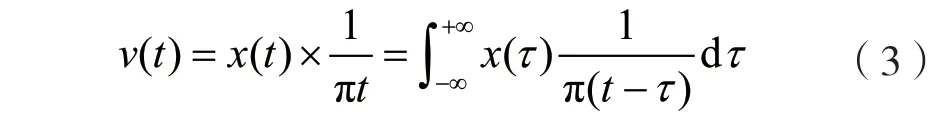
式中：τ為沖激響應因子。

由式（2）的變換，就可以對調制信號進行幅度、相位、頻率等信息的提取，得到信號的瞬時幅度

2 瞬時特征提取

通信信號的瞬時信息包括瞬時幅度、瞬時相位、瞬時頻率及不同角度的統計特征值，其中瞬時幅度、瞬時相位、瞬時頻率包含著調制信息[7]。對通信信號做調制識別，需要對信號的幅度、相位、頻率信息特征進行提取。

由瞬時幅度A(t)、瞬時相位φ(t)、瞬時頻率f(t)的值，可進一步得到調制信號瞬時特征參數，本文主要使用3個特征參數，分別是瞬時幅度的譜密度最大值γmax、瞬時相位絕對值的標準偏差σap、瞬時頻率絕對值的標準偏差σaf。

2.1 瞬時幅度的譜密度最大值

瞬時幅度的譜密度最大值γmax表征了信號瞬時幅度的變化情況，用來反映調制信號包絡的變化特性[8]，其表達式為：

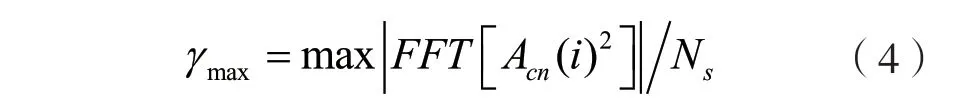
式中：Ns為數字信號的采樣點數；Acn(i)為歸一化瞬時幅度，Acn(i)=An(i)-1，An(i)=A(i)/ma，為瞬時幅度A(i)的平均值，用平均值對瞬時幅度進行歸一化的目的是消除信道增益的影響。

圖1展示了瞬時幅度的密度最大值，通過圖1可以得出頻移鍵控（Frequency Shift Keying，FSK）信號無包絡起伏、相移鍵控（Phase Shift Keying，PSK）信號有微弱的包絡起伏、幅移鍵控（Amplitude Shift Keying，ASK）信號包絡起伏較大，因此通過包絡值可以區分PSK、FSK、ASK信號。

圖1 瞬時幅度的譜密度最大值

2.2 瞬時相位絕對值的標準偏差

σap為相位絕對值的標準偏差，表示信號瞬時絕對相位的變化情況，其計算方式為：

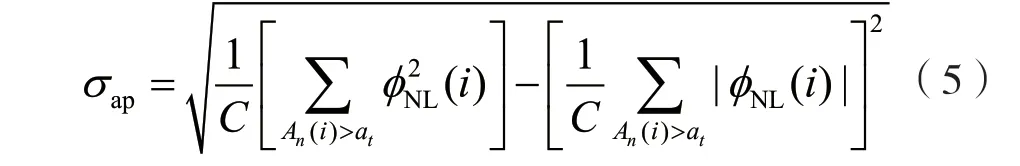
式中：C為非弱信號值的個數；An(i)為信號瞬時幅度的平均值；at為判斷弱信號的門限值，用于去除噪聲對微弱信號的影響；?NL(i)為經過零中心化處理后瞬時相位的非線性分量，在載波完全同步時，可表示為?NL(i)=?(i)-?0，其中，，?(i)表示無折疊瞬時相位。

圖2展示了瞬時相位絕對值的標準偏差，從圖2 中可以得知，σap可區分4PSK與2PSK和ASK信號。由于ASK信號不包含絕對相位信息，2PSK信號只有兩個瞬時相位值，經過零中心化處理后相位絕對值為常數，故也不含絕對相位信息，而對于4PSK信號，它含有4個瞬時相位值，因此其零中心化處理后相位絕對值不為常數，包含絕對相位信息，所以通過判斷相位絕對值是否趨近于零可以識別類內信號2PSK、4PSK。

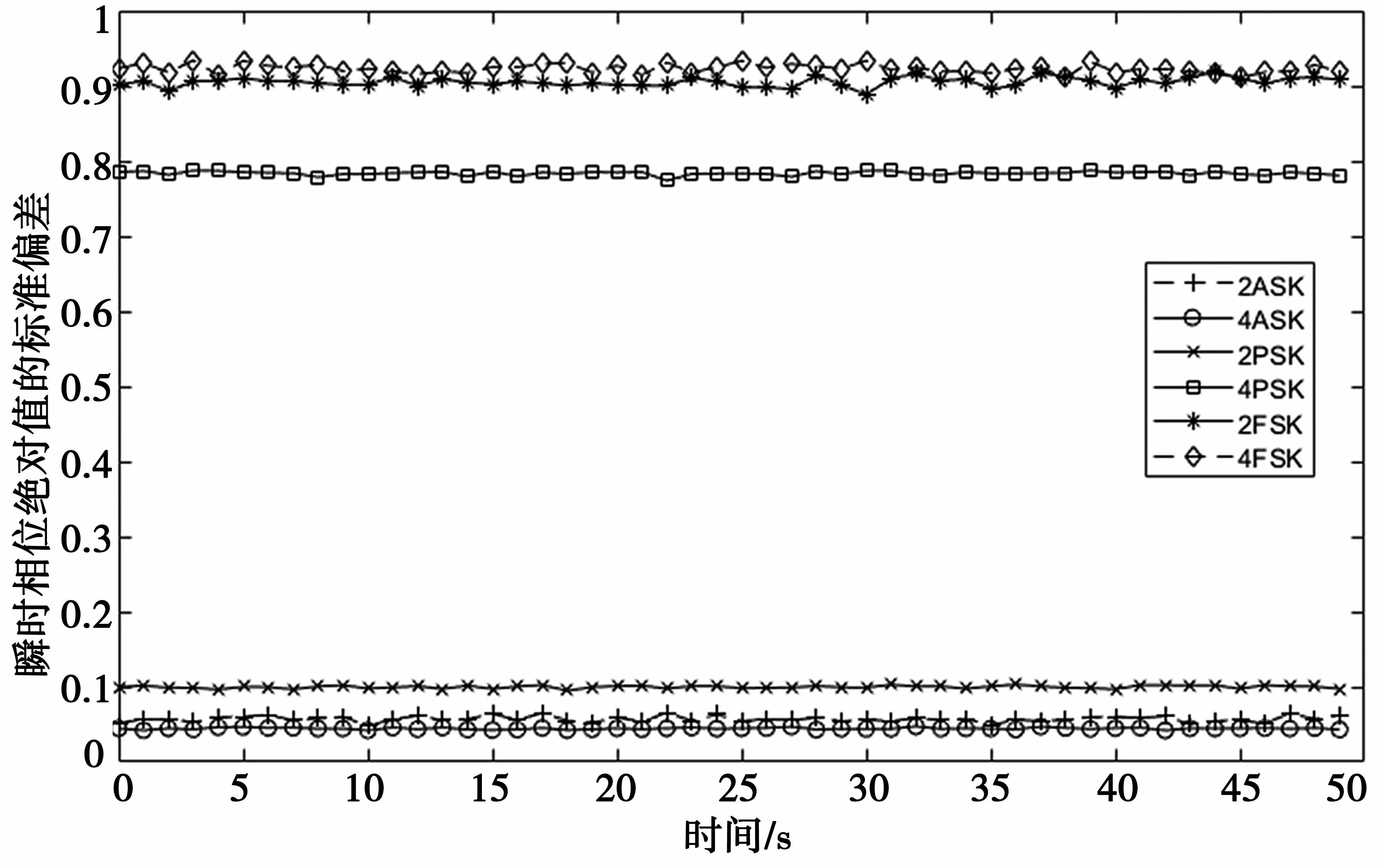
圖2 瞬時相位絕對值的標準偏差

2.3 瞬時頻率絕對值的標準差

瞬時頻率絕對值的標準差σaf表征信號的絕對頻率信息，可用來區分2FSK信號和4FSK信號。

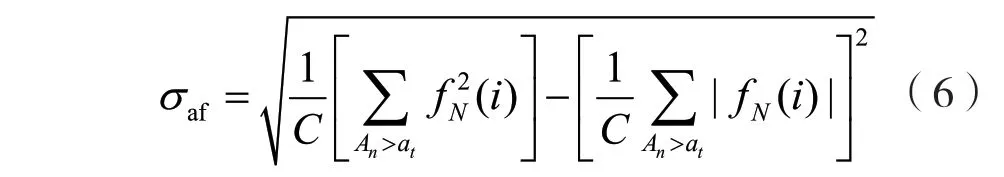
圖3展示了瞬時頻率絕對值的標準差，由圖3可知，2FSK信號的歸一化瞬時頻率的絕對值為常數，而4FSK信號的瞬時頻率有4個，歸一化后的絕對值不為常數，可區分出2FSK、4FSK、2ASK、4ASK信號。

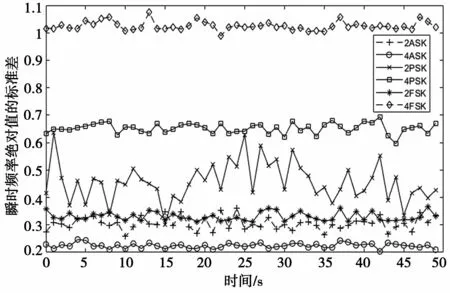
圖3 瞬時頻率絕對值的標準差

3 算法描述

目前，工程應用中大多使用決策樹，決策樹在工程應用中的優點是易于工程實現、設計流程較為簡單，缺點是門限設置較為復雜、人工操作容錯率較高、低信噪比下對數字通信信號的識別誤差大[9-11]。

針對低信噪比識別誤差大與決策樹算法設置門限復雜等問題，本文使用神經網絡作為分類器，可彌補以上缺點。目前，神經網絡在調制識別領域被廣泛應用，并在學術研究中獲得很大的突破，但在工程應用中很難實現，主要原因是深度神經網絡設計較為復雜，使用硬件資源較高且不易集成到實際工程中。而本文選用TFCNNC主要是利用神經網絡算法的分類識別功能，不進行卷積運算，進一步提取信號特征。

3層神經網絡是神經網絡的一種[12,13]，它是一種模仿動物神經網絡行為特征，進行分布式并行信息處理的算法數學模型。圖4展示了一個3層全連接神經網絡的結構，“Input”表示輸入層，“Layer”表示全連接層，“Output”表示輸出層，TFCNNC在結構設計中未使用卷積層，這樣做可以減少計算的復雜度，大大減少訓練的時間。x(i)表示瞬時特征參數γmax，σap，σaf的數據，y(i)表示網絡輸出信號的類型。TFCNNC在工程中的構建方式如下：

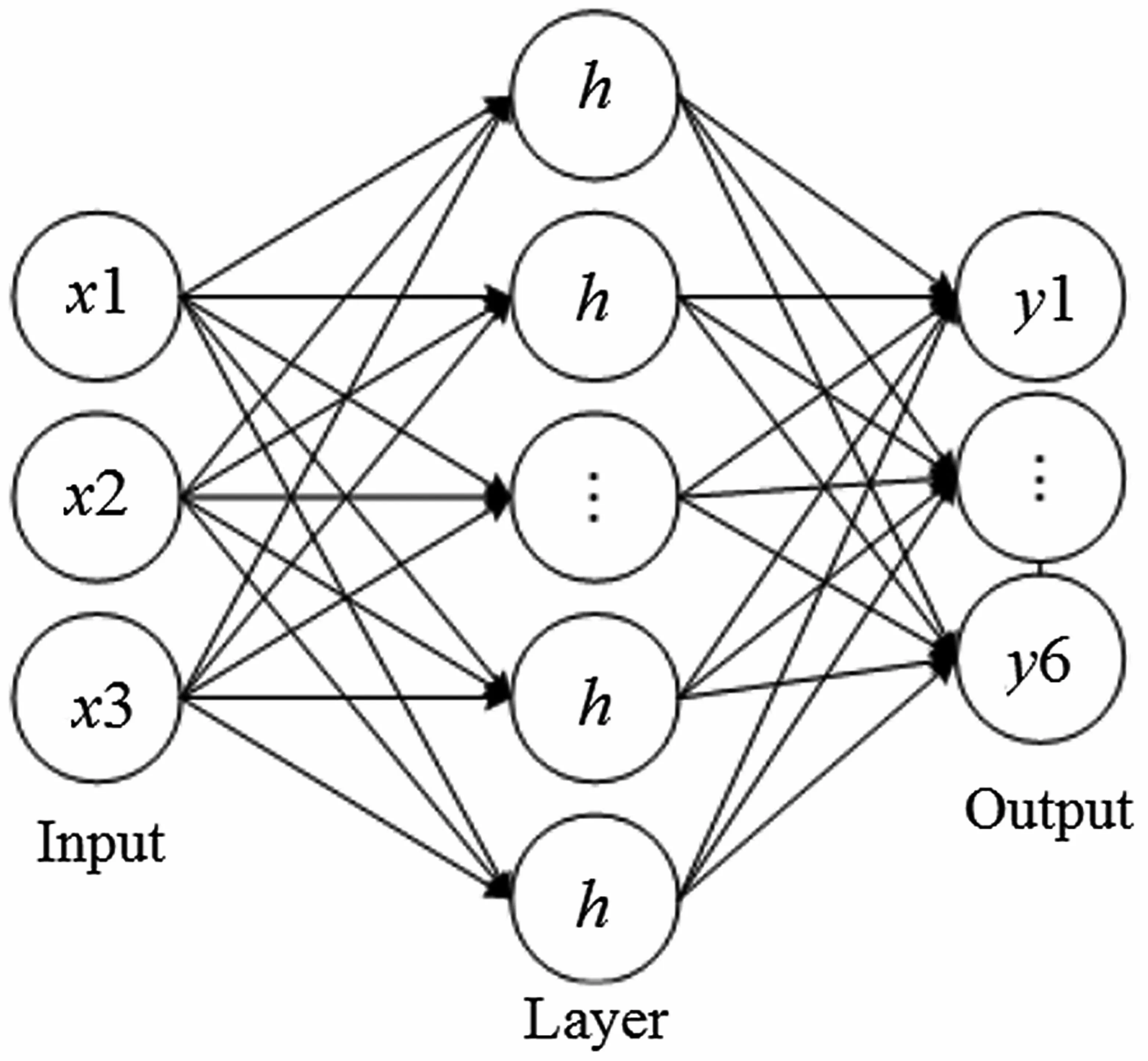
圖4 3層全連接神經網絡

（1）輸入層3×600×1,歸一化的數據長度為600，3種瞬時特征參數；

（2）全連接層1×1×50，可學習參數權重50×1 800，偏置50×1，步長為1，無填充；

（3）批量歸一化與ReLu層1×1×50；

（4）FullyConnected 1×1×6；

（5）Softmax分類器1×1×6；

（6）Output分類輸出1×1×6。

使用TFCNNC，其主要優點是網絡結構簡單，可以集成到工程中，低信噪比下識別率較高；缺點是需要先訓練模型，耗時較長。根據本文所采用的3個特征參數，使用TFCNNC對2ASK、4ASK、2FSK、4FSK、2PSK、4PSK信號進行識別。

從圖5展示的算法原理中可知，數據預處理主要是對數字通信信號求瞬時特征的γmax，σap，σaf，訓練模型主要是把預處理的信號進行訓練，得到網絡的權重和偏置項[14,15]，權重和偏置共同組成訓練模型，驗證識別主要是將訓練模型的權重和偏置直接應用于全連接層，將未知信號經過數據預處理后經過驗證識別出最終結果。具體識別步驟：首先對接收到的數字通信信號做下變頻處理；其次求解瞬時特征參數的3個特征值γmax，σap，σaf；再次訓練模型得到訓練后的權重和偏置；最后將訓練好的權重和偏置加載到驗證識別模型，從而得到最終的識別結果。其算法原理如圖5所示。

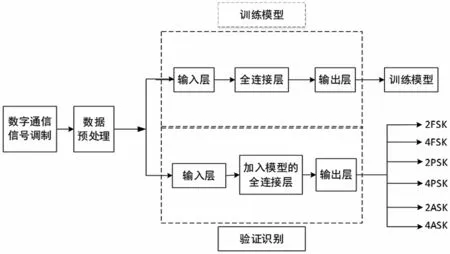
圖5 算法原理

4 仿真及結果分析

為驗證上述分析，進行仿真實驗，驗證低信噪比下決策樹與本文算法的識別結果。在載波同步條件下，對信號添加高斯白噪聲，載波頻率設置為 70 MHz，采樣頻率為200 MHz，符號速率10 MHz，信噪比的范圍是0～20 dB，仿真信號有2ASK、4ASK、2FSK、4FSK、2PSK、4PSK等6種。每 類信號產生了600組瞬時特征參數，每類信號隨機抽取200組數據作為驗證，將生成的數據以3×600的數組送入TFCNNC的輸入層，通過全連接層分類識別后，再經過softmax分類器即可得到分類結果。圖6是3層全連接網絡分類器的訓練過程。

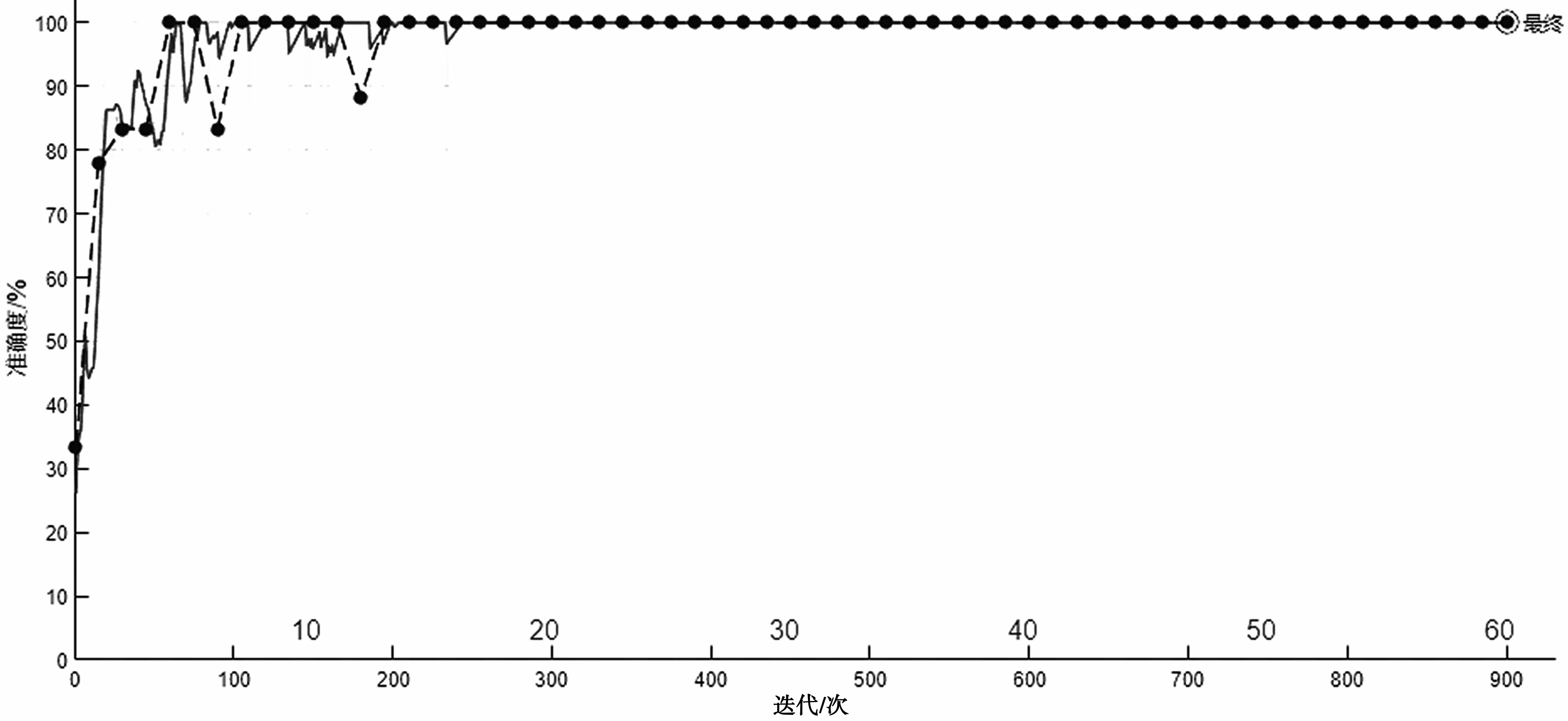
圖6 網絡訓練過程

在信噪比較低時，參數特征不能有效地區分調制類型，當信號低于5 dB時，決策樹算法[10]的識別效果較差，識別率受噪聲影響較大。在相同信噪比下，本文算法有更好的識別性能，每類信號的識別率相加取均值得到該信號的平均識別率，識別結果如圖7所示。神經網絡分類器識別算法和決策樹算法在不同信噪比下各種信號的識別率分別如表1、表2所示。

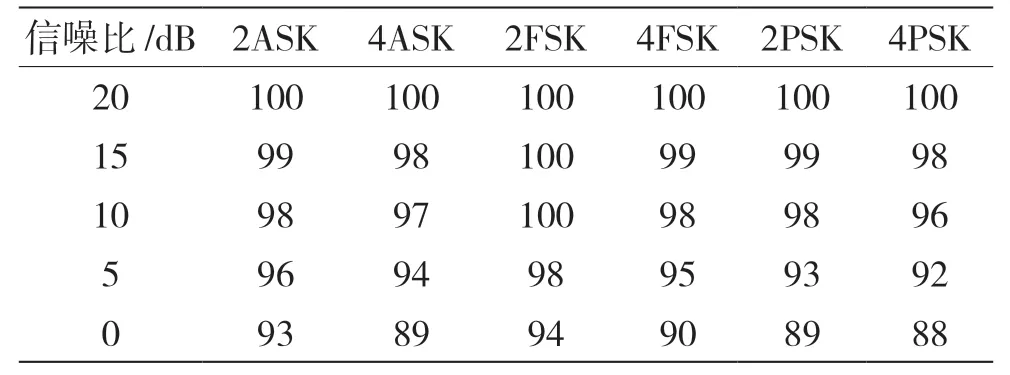
表1 神經網絡分類器算法識別結果 %

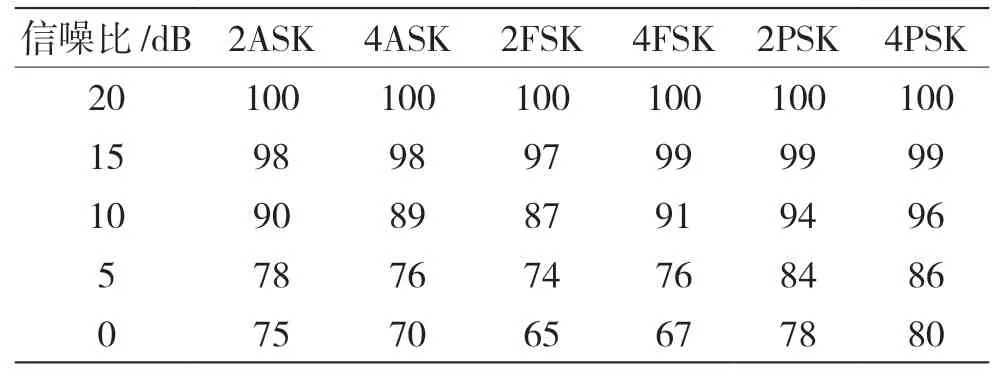
表2 決策樹算法識別結果 %

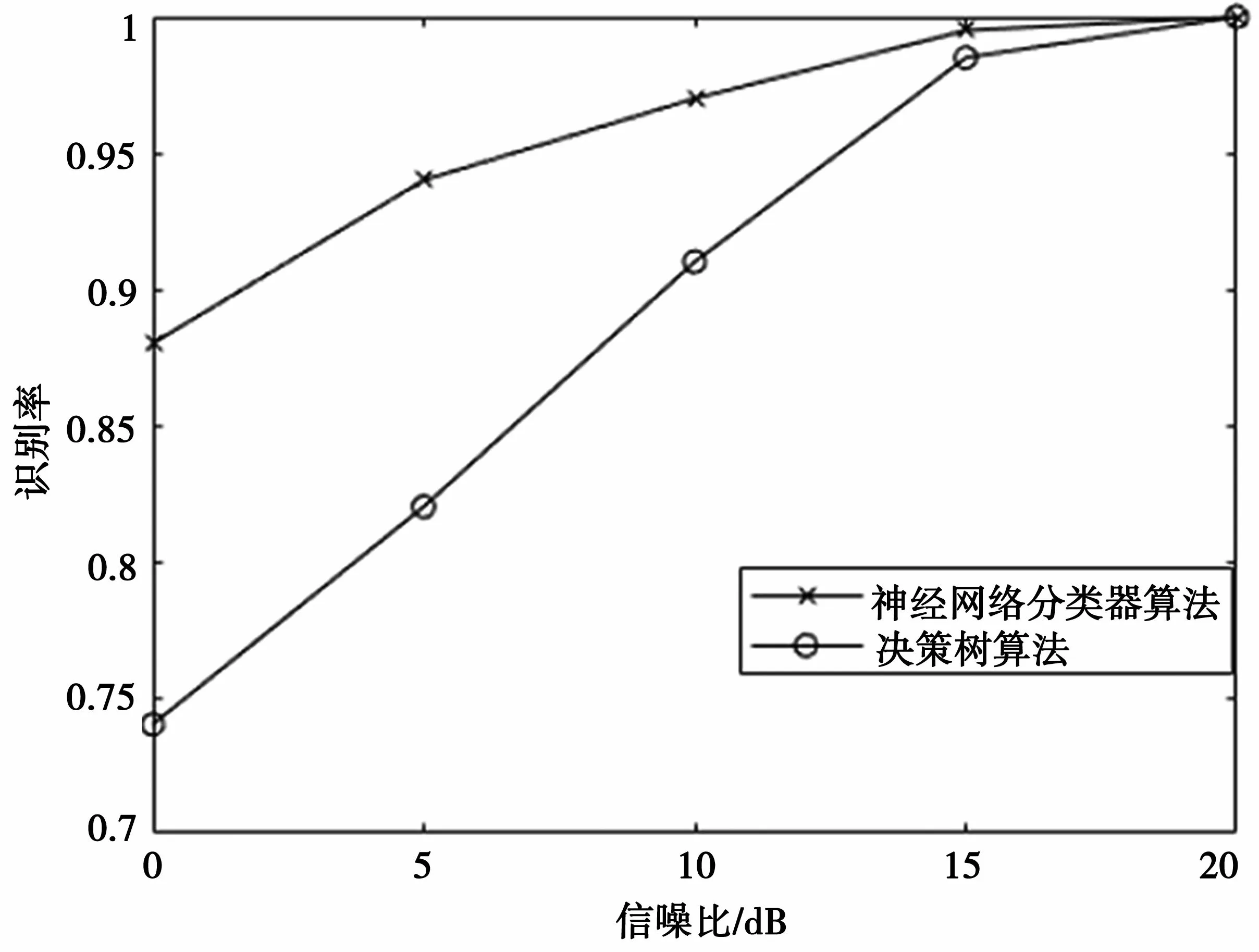
圖7 不同信噪比下信號識別率

由圖7、表1、表2可以得出，本文算法在15 dB 時各種數字通信信號的識別率均大于98%，10 dB時各種數字通信信號的識別率均大于96%，5 dB時各種數字通信信號的識別率均大于92%，0 dB時各種數字通信信號的識別率均大于88%。

5 結語

本文主要利用瞬時特征參數與TFCNNC相結合，具有低信噪比、高識別率、可集成到工程中的特性。整體算法的設計流程主要是，首先對數字通信信號進行數據預處理，選擇數據預處理的瞬時特征的3個參數；其次，將瞬時特征參數送入3層全連接神經網絡進行模型訓練，得到訓練好的權重系數和偏置系數；最后，將訓練好的權重系數和偏置系數應用到驗證識別過程。通過仿真驗證了該方法的有效性，實驗結果表明該方法在低信噪比時，相較于其他方法具有更高的識別率。下一步將研究如何把輕量化網絡應用到實際工程。