一種改進的樽海鞘群算法*
鄭洪清,謝 聰,周永權
(1.廣西職業師范學院教育學院,廣西南寧 530007;2.廣西農業職業技術大學,廣西南寧 530007;3.廣西民族大學人工智能學院,廣西南寧 530006)
群智能算法在許多領域發揮著重要的作用,近年來各種受自然界生物群體行為啟發的群智能算法被提出,如布谷鳥搜索(Cuckoo Search,CS)算法[1],灰狼優化(Grey Wolf Optimizer,GWO)算法[2]和鯨魚優化算法(Whale Optimization Algorithm,WOA)[3]等。Mirjalili等[4]根據樽海鞘群的覓食行為提出一種樽海鞘群算法(Salp Swarm Algorithm,SSA),因其原理簡單和易于實現,已成功應用于多個領域[5,6]。然而,樽海鞘群算法與其他群智能算法一樣,必須克服求解精度低和易陷入局部最優等缺點。諸多學者針對這一缺陷提出各種改進策略,如白鈺等[7]提出基于自適應慣性權重的樽海鞘群算法,引入慣性權重和差分變異思想提高算法性能;陳連興等[8]提出一種改進的樽海鞘群算法,對領導者引入加權重心取代最優個體位置和對個體逐維隨機差分變異,改進了算法的尋優性能,但這兩種算法的Rosenbrock函數求解精度較低。張鑄等[9]提出基于自適應正態云模型的引力樽海鞘群算法,結合引力搜索技術和正態云發生器有效提高收斂精度,全局搜索能力大大增強,但局部搜索能力相對較弱。王彥軍等[10]提出改進的樽海鞘群算法及其在焊接梁問題中的應用,利用精英反向學習、差分策略和Gauss變異為算法全局搜索奠定基礎;康俊濤等[11]提出基于樽海鞘群算法的桁架結構優化設計,在搜索過程中引入個體歷史信息改進算法,但算法改進效果不明顯。周新等[12]提出融合黃金正弦混合變異的自適應樽海鞘群算法,通過黃金正弦算法(Golden Sine Algorithm,Gold-SA)替換樽海鞘群算法領導者位置更新方式,并融合鄰域重心反向學習與柯西變異,改善算法性能,測試函數較為簡單。范千等[13]提出一種改進的樽海鞘群算法,采用折射反向學習機制和自適應控制因子提高優化性能;陳忠云等[14]提出基于混沌精英質心拉伸機制的樽海鞘群算法,采用Tent混沌和精英質心拉伸機制增強全局搜索能力;張嚴等[15]提出基于Levy飛行策略的改進樽海鞘群算法,對領導者位置進行Levy飛行更新,但以上算法求解精度較低。
雖然上述改進算法與基本SSA相比在性能上有了一定程度的改善,但求解精度還有提升空間。因此,本研究提出一種改進的樽海鞘群算法(Improved Salp Swarm Algorithm,ISSA),通過在追隨者階段引入差分進化策略和黃金正弦機制,共同增強算法尋優能力。通過23個基準函數測試,驗證ISSA算法的有效性。
1 樽海鞘群算法
樽海鞘群算法是模擬樽海鞘群覓食行為而衍生的一種群智能算法,在SSA中領導者引導群體進行食物搜索,其位置更新公式為
(1)
c1=2e-(4×l/lmax)2,
(2)
其中,Fj表示第j維領導者位置;c1是平衡全局搜索和局部搜索的重要參數,在迭代前期c1值較大有利于全局搜索,在迭代后期c1值較小有利于局部搜索;c2,c3∈[0,1];ubj,lbj表示第j維的上下界;l表示當前迭代次數;lmax表示最大迭代次數。
追隨者緊隨領導者后并依次形成鏈式結構,其位置更新公式為
(3)
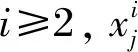
2 改進的樽海鞘群算法
2.1 改進領導者方式
基本SSA中,領導者完全依靠式(1)進行搜索,若領導者陷入局部最優,則追隨者必陷入局部最優。因此考慮對領導者第j維值采用隨機維度以拓展種群多樣性,有利于算法跳出局部最優,故領導者位置更新公式修改為
k=randperm(n),
(4)
(5)
其中,n為問題維數,randperm為生成不重復的隨機整數。
2.2 改進追隨者方式
在基本SSA中,當前追隨者位置僅取自身位置和上一個位置的平均值,若追隨者緊密相連,則不利于全局搜索,且未利用群體之間的交流信息,因此考慮對追隨者采用差分進化策略進一步拓展種群多樣性。首先剔除種群中領導者位置,從剩下種群中隨機生成3個不同位置的追隨者進行差分進化操作,具體計算公式如下:
(6)
其中,r1,r2,r3為追隨者中任意一個,且r1≠r2≠r3,b∈[0,1]為控制變異概率。
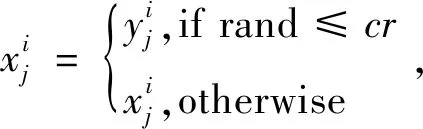
(7)
其中,cr∈[0,1]為控制交叉概率。
2.3 黃金正弦算法
黃金正弦算法是Tanyildizi等[16]提出的一種元啟發式算法,該算法基于正弦函數和單位圓的關系求解優化問題。Gold-SA遍歷單位圓上所有點,因而具有較強的全局搜索能力,而且在全局最優位置和當前位置采用黃金分割系數,因此也具有較強的局部搜索能力。Gold-SA位置更新公式為
(8)
其中,r1∈[0,2π]內的隨機數,r2∈[0,π]內的隨機數,x1=-π+(1-τ)×2π,τ為黃金分割系數,
x2=-π+τ×2π。為進一步提升Gold-SA局部搜索能力,在自身位置引入自適應慣性權重式(2),因此最終Gold-SA位置更新公式為
(9)
2.4 ISSA偽代碼
輸入:種群規模N,函數名稱及最大迭代次數,設置變異概率b和交叉概率cr,計算黃金分割系數。
①在領域范圍內隨機產生初始種群,計算其最優值及食物源位置。
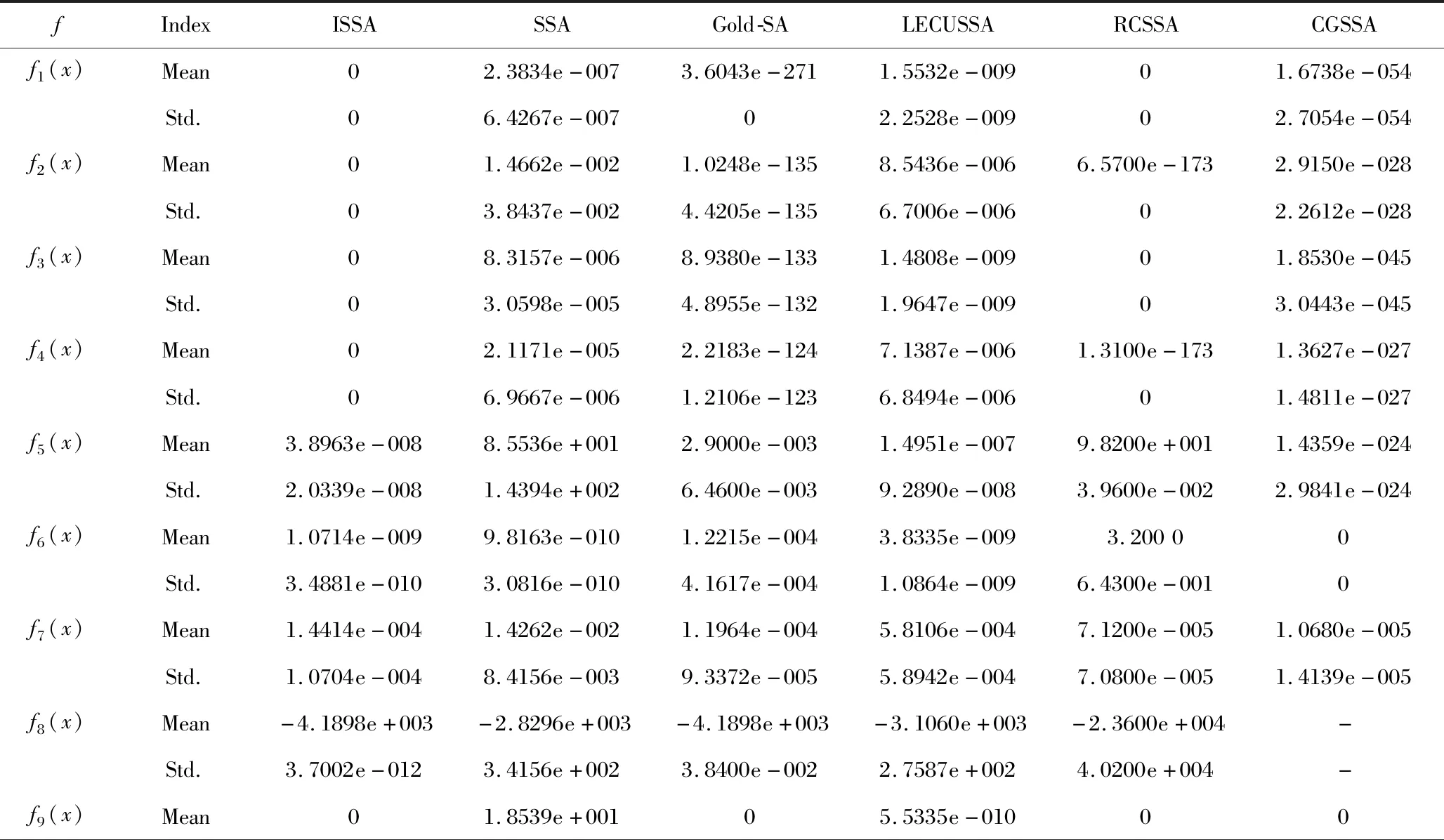
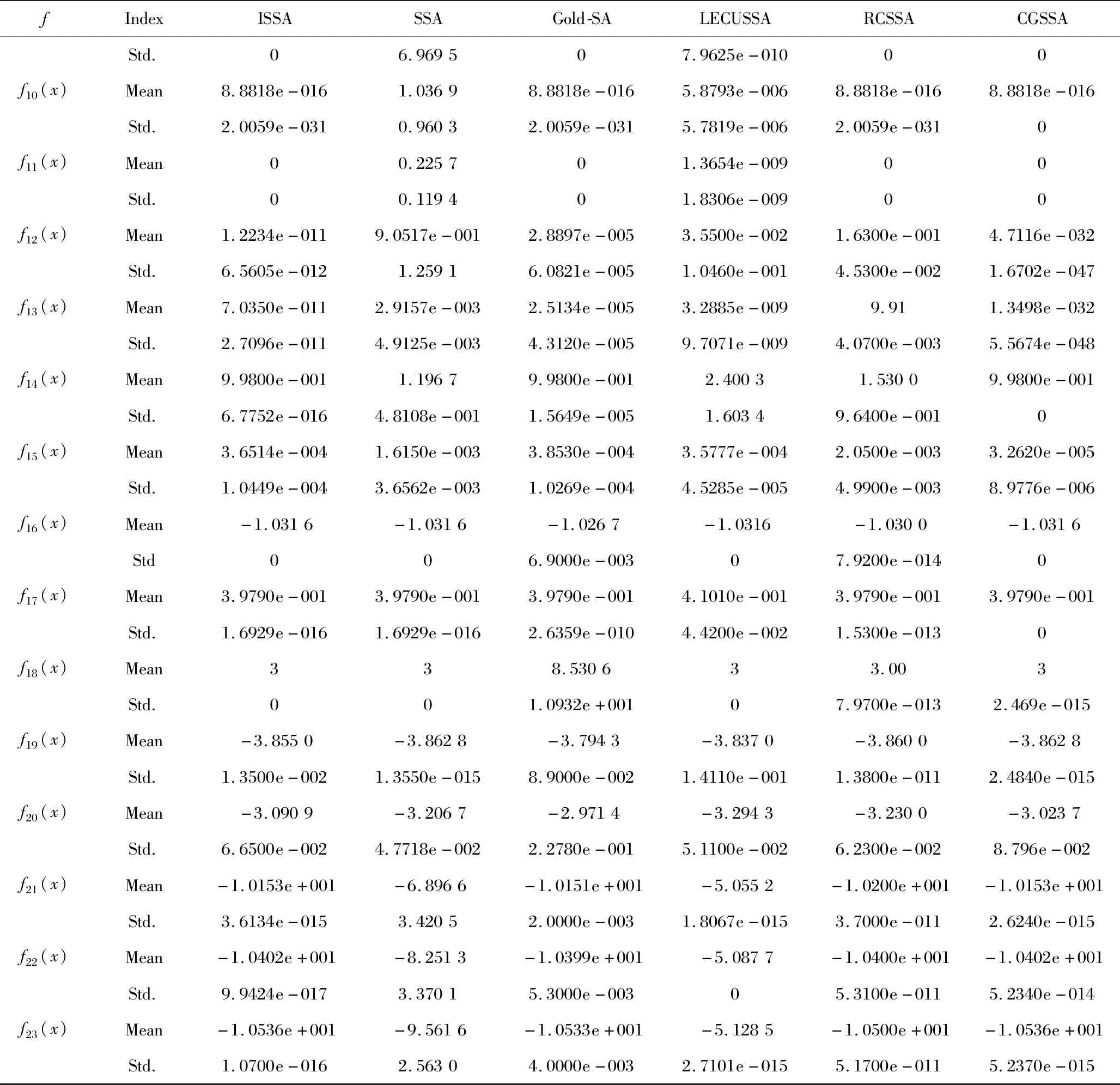
②Whilel ③ 計算式(2); ④ Fori=1∶N ⑤ Ifi≤N/2i ⑥ 執行式(4)、式(5); ⑦ Else ⑧ If rand ⑨ 執行式(6)、式(7); (3)氧化鋅回收技術仍需改進,火法回收應注重解決生產過程中能耗高且氧化鋅純度較低等問題,還應注重解決回轉窯內結圈問題。酸法回收過程產生的廢酸回收處理有待研究,氨法回收過程中產生的氨氣直接排放造成大氣污染,因此回收并處理氨氣也是氨法回收氧化鋅的重要研究內容 ⑩ Else 在ISSA中只是一定概率下執行式(6)、式(7)和式(9),并替換基本SSA中的式(3),因此并沒有增加算法的時間復雜度。 為檢驗ISSA的性能,選取文獻[9]中23個基準函數進行測試,并將其計算結果與基本SSA、Gold-SA和改進算法LECUSSA[15]、RCSSA[13]及CGSSA[9]進行比較,以驗證ISSA綜合改進策略的效果。為公平比較,所有算法的參數設置如下:N=30,lmax=500,b=0.2,cr=0.1,其余參數設置與原文獻相同。每種算法在Matlab 2016a軟件中獨立運行30次,計算每個函數的平均值(Mean)和方差(Std.),Mean和Std.越小,則性能越佳,結果如表1所示。 表1 基準函數的實驗結果Table 1 Experimental results of benchmark functions 續表Continued table 從表1可知,ISSA與基本SSA和Gold-SA比較,在7個單峰函數(f1-f7)測試下,ISSA的計算結果除函數f6比SSA、函數f7比Gold-SA差且相差甚微以外,其余5個函數的計算結果均優于SSA和Gold-SA,其中函數f1-f4達到理論值,函數f5的計算結果分別比Gold-SA和SSA高出5個和9個數量級,可見ISSA局部勘探能力優異。在6個多峰函數(f8-f13)測試下,ISSA的計算結果都優于SSA,有3個函數的計算結果與Gold-SA相等,有3個函數的計算結果優于Gold-SA,可見ISSA全局搜索能力更強。在10個固定維多峰函數(f14-f23)測試下,ISSA的計算結果除函數f19和f20比SSA稍差以外,大多數函數的計算結果均優于SSA或Gold-SA,證明ISSA全局搜索能力優異。 再將ISSA與改進算法LECUSSA、RCSSA及CGSSA進行比較,LECUSSA僅函數f15、f20求解結果比ISSA優越且差別不大,其余21個函數中有2個函數(f16、f18)求解結果與ISSA一致,另外19個函數求解結果均比ISSA算法差;RCSSA有5個函數(f1、f3、f9、f10、f11)求解結果與ISSA一致,有3個函數(f7,f19,f20)求解結果優于ISSA,其余函數求解結果均比ISSA差;除函數f8外,CGSSA有8個函數(f1-f4、f18、f20、f22、f23)求解結果比ISSA差,有3個函數(f9、f11、f16)求解結果與ISSA相等,其余11個函數求解結果優于ISSA。因此,總體來看,ISSA優于LECUSSA和RCSSA,次于CGSSA。 為直觀展示ISSA的收斂速度和計算精度,給出部分函數平均收斂曲線如圖1所示;為便于比較,縱坐標取平均函數值對數。從圖1可知,ISSA的平均收斂曲線速度比SSA快,計算精度比SSA高;但在迭代前期ISSA收斂速度慢于Gold-SA,這是由于在迭代前期ISSA以大概率執行差分進化策略,而在迭代后期ISSA收斂速度明顯優于Gold-SA。 圖1 函數收斂曲線Fig.1 Convergence curve of function 本研究提出了一種改進的樽海鞘群算法,通過在領導者位置引入隨機維度以拓展種群多樣性。在算法前期,追隨者以較大概率執行差分進化策略,進一步增強種群多樣性;在算法后期,追隨者以較大概率執行黃金正弦算法,同時在黃金正弦算法自身位置引入自適應慣性權重增強局部勘探能力。使用23個基準函數評估算法,結果表明ISSA尋優性能優于基本SSA和Gold-SA,同時與其他改進的樽海鞘群算法相比,ISSA算法也具有一定優勢。2.5 ISSA時間復雜度分析
3 仿真實驗與結果
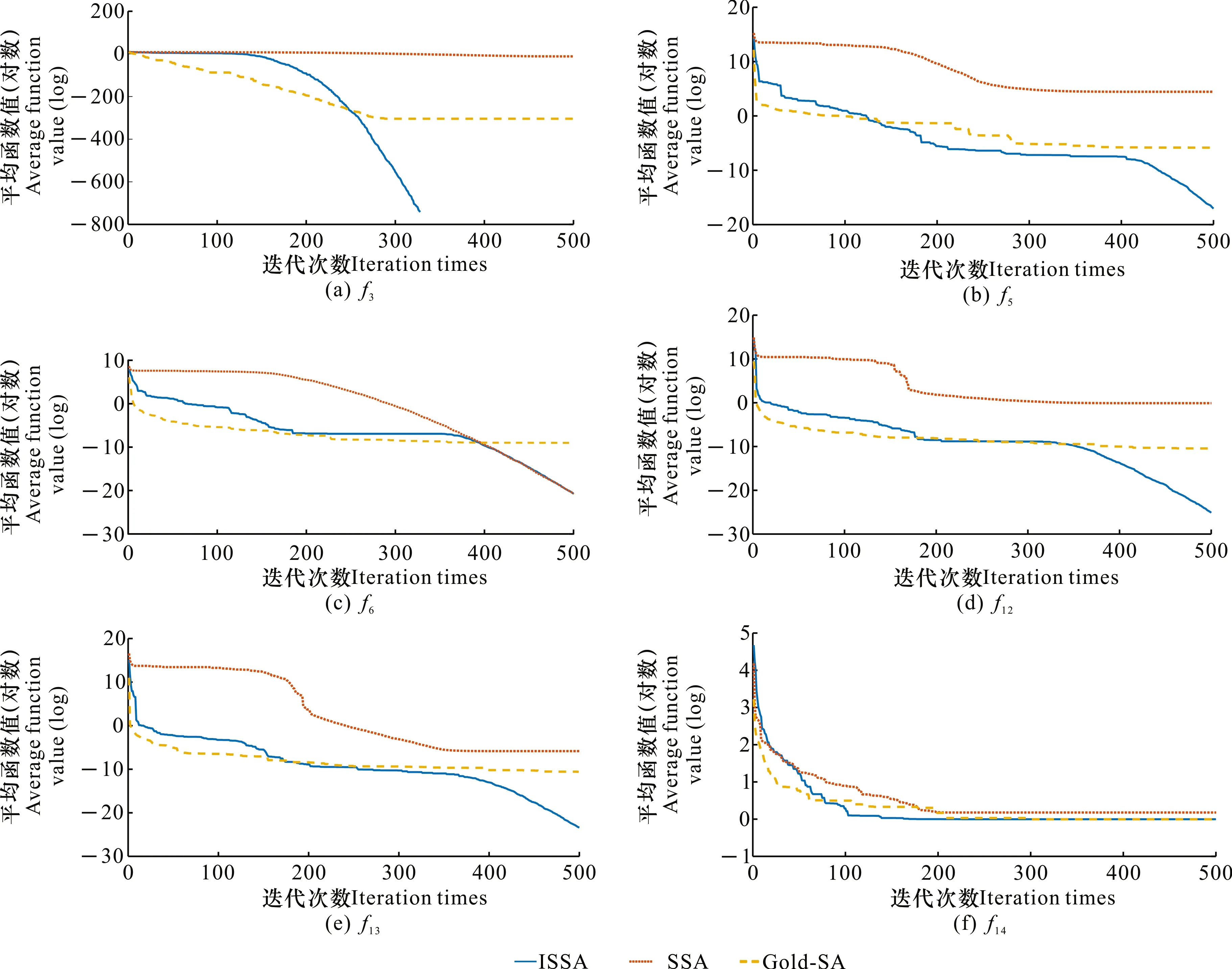
4 結論

