基于CEEMDAN分解的短時交通流組合預測

聶 鈴，張 劍，胡茂政

上海工程技術大學 航空運輸學院，上海 201620

隨著經濟的快速發展和城市化的不斷推進，汽車保有量高速增長，道路交通擁堵成為焦點問題。智能交通系統（intelligent transportation system，ITS）在實時交通信息基礎上，通過交通流誘導和控制，達到減少交通擁堵現象，節約出現時間的目的[1]。高效且準確的道路交通預測系統是ITS的重要組成部分[2]，如何確保短時交通流預測的效果成為了當前交通流預測領域的難點，同時也是交通研究方向的熱點之一。

近年來，國內外眾多學者在短時交通流預測的研究方向大多采用了智能算法組合優化的方法。馬秋芳在傳統的神經網絡基礎上，引入優化后的粒子群算法建立模型[3]；Qian等人利用遺傳算法對神經網絡的初始參數改進后進行交通流預測[4]；Lu等人采用滾動回歸ARIMA模型與長短期記憶（long short-term memory，LSTM）模型結合進行預測[5]；楊剛等人利用優化后的粒子群與最小二乘支持向量機結合進行交通流預測[6]。這些研究表明了智能算法組合優化進行短時交通流預測效果較好，隨著對交通流時間序列特點的深入研究，時間序列分解方法在交通流研究領域廣泛應用。殷禮勝等人提出交通流經過經驗模態分解后與改進粒子群算法優化LSSVM的組合預測算法[7]；肖進麗等人采用經驗模態分解結合差分進化組合優化BP神經網絡進行交通流預測[8]；Tian等人經過經驗模態分解后，在極限學習機的基礎上，結合ARIMA算法，提出一種新的混合短時交通流預測模型[9]。雖然這些短時交通流預測模型預測效果得到了提高，但很少有針對分解后的各個交通流時間序列分量的特點，建立與其適應的組合預測模型，因此如何將時間序列分解方法與預測模型更好地結合成為了交通流預測的熱點研究法方向之一。

在此基礎上，本文提出了基于CEEMDAN分解的短時交通流組合預測模型。首先鑒于交通流的不確定性和非線性，采用CEEMDAN算法對交通流時間序列進行分解；其次，利用PE算法對分解后的各個交通流時間序列分量分析的隨機特性，根據時間序列分量的不同隨機特性分為高頻序列分量、中頻序列分量和低頻序列分量，根據高頻、中頻和低頻序列分量的隨機特性分別建立GWO-BP模型、GWO-LSSVM模型和ARIMA模型進行預測；最后疊加各個高頻、中頻和低頻序列分量的預測結果，得到短時交通流最終預測值，并分析比較基于CEEMDAN分解的短時交通流組合預測結果與ARIMA模型、BP模型、LSSVM模型以及GWO-LSSVM模型的預測結果。

1 理論與方法

1.1 CEEMDAN算法

經驗模態分解法（EMD）方法是一種處理非平穩信號的方法，根據波動尺度將復雜的原始序列分解成不同賦值的IMF分量。但EMD方法在信號分解過程中會顯現模態混疊現象[10]，為解決這一問題，鑒于白噪聲均勻分布的特點，Wu等人在分解過程中加入白噪聲，提出了集合經驗模態分解法（EEMD）[11]，但分解后殘留的白噪聲導致EEMD方法分解具有較差的完整性。Torres等人提出了自適應噪聲完全集合經驗模態分解（CEEMDAN）[12]，將自適應高斯白噪聲添加至每一階段，有效地解決了模態混疊以及重構序列中存在殘留噪聲的現象，具有較好的分解完備性。

1.2 PE算法

排列熵（permutation entropy，PE）是一種度量時間序列復雜性的方法，可以表示時間序列的隨機性和突變性。PE算法計算簡便且運算效率高，同時針對非線性序列數據穩定性高，具有較強的抗干擾特點。PE算法的基本原理如下：

首先對交通流時間序列{X(i),i=1,2,…,}n進行相空間重構，進而得到相空間矩陣Y為：

式中，m為嵌入維數，τ為延遲時間，j=1,2,…,k。

對于重構后的相空間矩陣Y，每一行向量都可以得到一組符號序列S(g)為：

式中，j1,j2,…,j m表示重構向量各分量元素所在的列序號，g=1,2,…,l且l≤m!。

計算每種符號序列S(g)出現的概率P g(g=1,2,…,l)，根據Shannon熵的形式，將交通流時間序列X(i)的第l種符號序列的排列熵H p(m)定義為：

式中，0≤H p(m)≤lnm!，當P j=1/m!時，H p(m)達到最大值lnm!。

為了方便，將H p(m)進行標準處理：

式中，0≤H pE(m)≤1，H pE(m)值的大小表示時間序列隨性程度。值越大則代表序列隨機程度越強，反之，隨機程度越弱，呈現的規律越明顯。嵌入維數m和延遲時間τ對PE算法有著重要影響。

1.3 BP算法

BP神經網絡算法是一種前饋神經網絡，主要學習方式為利用梯度下降算法不斷迭代來優化神經元之間的權值和閾值[13]。雖然其非線性映射能力較強，但隱含層神經元的權值和閾值是隨機分配的，網絡結構較大且包含大量可變參數，結果容易陷入局部最優解從而導致算法過早結束，并且收斂性較差。BP神經網絡包括三個網絡結構：輸入層、隱含層和輸出層[14]，輸入層X=[x1,x2,…,x N1]，隱含層Y=[y1,y2,…,y N2]，輸出層Z=[z1,z2,…,z N3]，以全連接的方式連接各層之間。

1.4 LSSVM算法

SVM是應用于時間序列預測研究的一種有效模型，最小二乘支持向量機（least-squares support vector machine，LSSVM）[15]是對SVM模型的改進。LSSVM的損失函數為最小二乘線性系統，為了減少了求解過程中的計算量，采用等式約束，改變了SVM中的不等式約束。與其他預測模型相比，最小二乘支持向量機模型可以改善過度學習和訓練時間長的缺點，在解決非線性問題時具有更好的精度和準確度。LSSVM的優化模型如下：

1.5 ARIMA算法

ARIMA模型是預測平穩時間序列的最常用的線性回歸模型之一，由Ziegel、Box和Jenkins提出[16]。ARIMA模型雖然結構簡單以及計算簡便，但適用波形較為穩定的交通流數據[17]。ARMA模型通常用來分析時間序列，用ARMA(p,D,q)來表示該模型，其中p、D、q表示預測模型的結構參數，分別為自回歸AR(p)、差異度D和移動平均MA(q)。當時間序列表現為較穩定時，ARMA模型能很好地進行原始數據擬合。然而，當時間序列表現為不穩定時，則需要采用差分轉換過程將其轉換成穩定的時間序列。ARIMA模型用于模擬差分時間序列，所以也適用于不平穩序列，這個過程為ARIMA(p,d,q)，用數學表達式表示為：

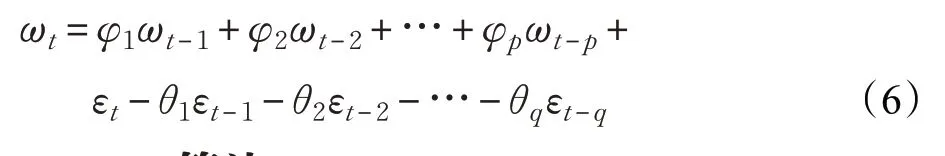
1.6 GWO算法

灰狼算法（grey wolf optimizer，GWO）是由Mirjalili等人在2014年提出的一種新群體智能算法[18]，主要學習方式是模擬狼群在自然界中的種群層次結構和捕食活動。GWO算法相對于其他算法，具有較強的收斂性和穩定性。GWO算法具有接近任何非線性函數的能力，且存在參數少、全局搜索能力強的優勢[19]。同時GWO算法適應性強且操作簡便，易于實現，同時與其他算法較容易結合，達到提高性能的效果。

GWO算法根據社會關系將整個狼群分為四個等級，第一級為α狼，屬于頭狼，負責決策，決定捕食、棲息地和時間，其他狼都必須服從α狼的命令。第二級為β狼，屬于協助狼，服從并協助α狼。第三級為δ狼，服從α狼和β狼，同時控制狼群的剩余部分。第四級為ω狼，ω狼沒有自主決策控制能力，它必須服從狼群其他等級的狼。前三級狼有著較好的適應能力，在α狼的引導下，有組織地對獵物進行跟蹤，圍捕和攻擊。GWO算法實現步驟如下：

假設灰狼狼群的規模為N，搜索空間為D維，第i只狼灰狼的位置表示為Xi=[x1(1),x2(2),…,xi(i)]，則狼群捕獵過程包括追蹤、狩獵和攻擊。灰狼在發現獵物后，逐漸靠近獵物并將其包圍，灰狼與獵物的距離是：

式中，t表示當前迭代次數，X(t)表示灰狼t次迭代后的位置矢量（即潛在解所在位置），Xp(t)表示獵物t次迭代后的位置矢量（即最優解所在位置），系數向量A和C的計算公式為：

式中，r1和r2表示0到1之間的隨機數，隨著迭代時間的增加，a從2減小到0。

根據α、β、δ這三種狼來估算獵物的位置，則其他狼的位置更新方法為：

2 基于CEEMDAN分解的短時交通流組合預測模型的建立

2.1 基于CEEMDAN分解的短時交通流組合預測模型

鑒于短時交通流時間序列具有較強非線性和隨機性，使用單一的預測方法進行交通流預測很難得到較好的預測效果。由于CEEMDAN分解具有良好的分解完備性，同時對原始交通流序列具有精準分解的優點，本文采用CEEMDAN分解方法對短時交通流序列進行分解得到多個分量，利用PE算法分析各個分量的隨機特性，將時間序列分量分為高頻、中頻、低頻分量。考慮到BP具備較強的非線性映射特征，采用BP算法對具有較強非線性和隨機性的高頻時間序列分量進行交通流預測，同時為了提高高頻序列分量預測效果，在BP算法的基礎上引入GWO算法優化其權值和閾值，建立GWOBP預測模型；考慮到LSSVM對于非線性波動數據具有較強的學習能力及較快的學習速度，因此采用LSSVM算法對具有一般非線性和隨機性的中頻時間序列分量進行交通流預測，同時為了提高中頻序列分量預測效果，在LSSVM算法的基礎上引入GWO算法優化其正則化參數和核函數參數，建立GWO-LSSVM預測模型；考慮到ARIMA對平穩序列具有良好的預測性能，因此采用ARIMA算法對較平穩的低頻時間序列分量進行交通流預測。最后疊加各個高頻、中頻和低頻序列分量的預測結果，得到短時交通流最終預測值。基于CEEMDAN分解的多分量組合短時交通流預測模型流程圖如圖1所示。

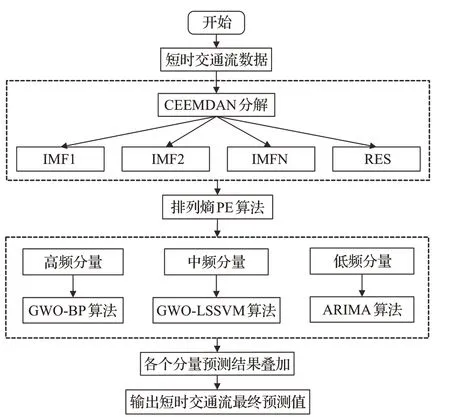
圖1 基于CEEMDAN分解的短時交通流組合預測模型Fig.1 Short-term traffic flow combination prediction model based on CEEMDAN decomposition

2.2 基于CEEMDAN分解的交通流時間序列

基于CEEMDAN分解的交通流時間序列實現步驟如下：

（1）在原始交通流時間序列y(n)加入服從標準正態分布高斯白噪聲序列v i(n)，信噪比為ε，經過第i次分解的交通流時間序列為y i(n)。

（2）利用EMD方法分解交通流量數據，獲得第1個模態分量取均值為IMF1(n)和第1個余量序列r1(n)。

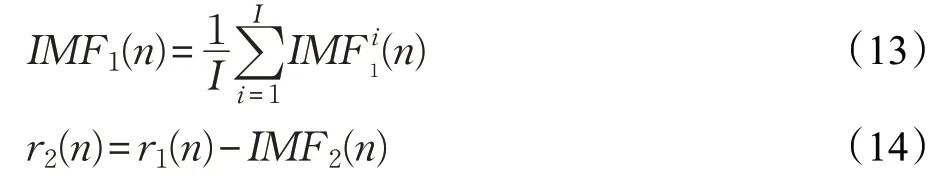
（3）進行EMD分解后的k階IMF分量交通流數據為E k(·)，第2個模態分量為IM F2(n)和第2個剩余分量序列為r2(n)。

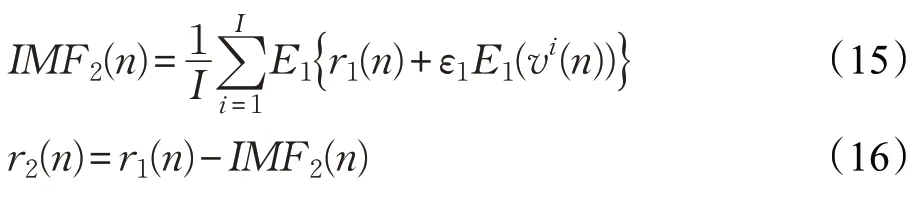
（4）第k個剩余分量序列為r k(n)和第k+1個IMF分量為IMF k+1(n)。

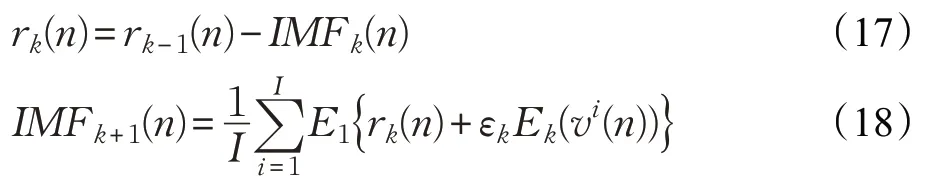
（5）重復以上步驟，直至余量不能分解，最終交通流時間序列被分解為y(n)。

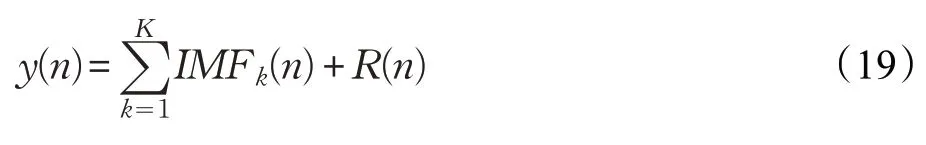
2.3 GWO-BP預測模型

GWO-BP算法的核心是將灰狼算法中種群位置信息設置為BP神經網絡的權值和閾值，當灰狼在追捕獵物過程中對獵物位置的判斷不斷更新自身的位置，不斷更新權值和閾值，最后找到最優解。針對高頻序列分量的GWO-BP預測模型實現步驟如下：

（1）進行BP神經網絡模型的構建。確定模型隱含層節點數目，輸入和輸出的參數，并對數據作預處理。

（2）GWO算法參數初始化。設定灰狼種群規模、種群搜索空間、位置信息維度、算法迭代的最大次數、灰狼狼群初始位置信息。

（3）確定適應度函數，對每個狼群個體進行BP神經網絡訓練，計算個體的適應度，從中選取適應度排名最高的3個灰狼，作為最優解xα、次優解xβ和第三優解xδ。

（4）更新余下灰狼ω狼個體的位置，同時計算并更新a、A和C參數。

（5）判斷是否達到步驟（2）設定的算法迭代的最大次數，若達到，則終止迭代，輸出最優灰狼α狼的位置，若未達到，則重復（3）至（4），直到達到步驟（2）算法迭代的最大次數。

（6）將求得的最優初始權值矩陣和閾值矩陣代入BP神經網絡模型，實現GWO-BP模型的建立。

（7）將預處理后的數據輸入至建立好的GWO-BP模型，即可得到各個高頻序列分量預測結果，與真實值進行對比，從而驗證該模型的可靠性。

2.4 GWO-LSSVM預測模型

GWO-LSSVM算法的核心是灰狼位置信息設置為LSSVM的正則化參數和高斯核函數，通過灰狼不斷更新位置，更新正則化參數和高斯核函數，找到最優解。針對中頻序列分量的GWO-LSSVM預測模型實現步驟如下：

（1）對數據進行預處理，通過歸一化處理將交通流原始數據修改為（-1，1）區間，同時將交通流時間序列分量數據劃分訓練集和測試集。

（2）GWO算法參數初始化。設定灰狼種群規模，種群搜索空間、位置信息維度、算法迭代的最大次數、灰狼狼群初始位置信息。

（3）確定適應度函數。對每個狼群個體進行LSSVM訓練，計算個體的適應度，由高到低排序，選取適應度排名最高的3個灰狼作為α狼、β狼、δ狼。

（4）更新余下灰狼ω狼個體的位置，同時計算并更新a、A和C參數。

（5）判斷是否達到步驟（2）預先設置的迭代的最大次數，若達到，則終止迭代，輸出最優灰狼α狼的位置，若未達到，則重復（3）至（4），直到達到預先設置的迭代的最大次數。

（6）將經過GWO算法獲得的正則化參數γ和核函數參數σ代入LSSVM模型，實現GWO-LSSVM模型的建立。

（7）將預處理后的數據輸入至建立好的GWO-BP模型，即可得到各個中頻序列分量預測結果，與真實值進行對比，從而驗證該模型的可靠性。

2.5 ARIMA預測模型

針對低頻序列分量的ARIMA預測模型實現如下：

（1）對低頻序列分量采用平穩性檢驗方法。首先觀察低頻序列分量的原始序列圖，對其進行平穩性驗證，如果該低頻序列分量表現為不平穩時，則反復對其進行差分處理，直至低頻序列分量表現平穩為止，該過程所進行的差分處理的次數即為ARIMA(p,d,q)中d的參數值。

（2）確定低頻序列分量預測模型的階數。通過觀察自相關圖以及偏自相關圖來確定ARIMA(p,d,q)中p和q的參數值，建立一個可行性模型。通過參數估計及診斷檢驗過程中，從所有可行性模型中選擇合適的模型。根據AIC和BIC準則選擇合適的ARIMA模型。

（3）對建立的低頻序列分量的預測模型診斷檢驗。驗證所建的模型是否適用于交通流時間序列，為了保證模型的殘差序列為白噪聲，對模型采用顯著性檢驗方法，同時進行假設檢驗。

（4）根據以上步驟，將確定的預測模型導出，作為預測的訓練模型。

3 仿真結果與分析

3.1 實驗數據的選取

在道路存在突發狀況、信號燈配時等眾多因素的影響下，道路交通流通常具有非線性和不確定性的特點。通過繪制一定時間內采集的交通流時間序列曲線，可以發現交通流具有周期性的特征，工作日（周一至周五）的交通流變化規律尤其相似。為了驗證基于CEEMDAN的組合預測模型進行短時交通流預測的有效性，本文的實驗數據來自于PeMS系統2018年6月4日—2018年6月8日5個工作日，5 min為采樣間隔的交通流數據。

首先對道路旁車輛檢測器采集的原始交通流數據進行預處理，數據處理后可以得到1 440個交通流量數據點。為了建立交通流預測模型，利用歷史數據預測下一時刻的交通流。以預測點前2 h的交通流序列作為模型輸入，以預測的交通流序列作為模型輸出。基于上述規則，前四個工作日的1 152個交通數據點可以建立1 128個輸入輸出數據集，構成模型的訓練集，第五個工作日的交通流數據點建立288個輸入輸出集，構成模型的測試集。交通流數據集分為訓練集和測試集，比例為4。采樣間隔為5 min，連續5個工作日的交通流時間序列曲線如圖2。

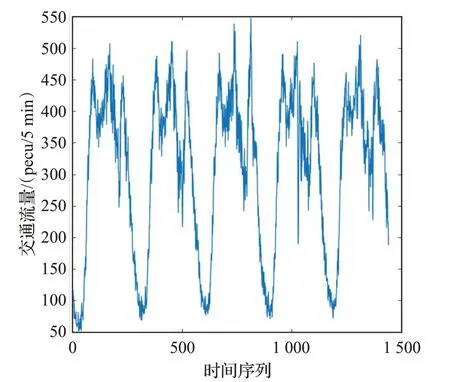
圖2 5個工作日的交通流時間序列曲線Fig.2 Time series curve of traffic flow in 5 working days

3.2 基于CEEMDAN算法的交通流時間序列分解

通過MATLAB軟件，采用CEEMDAN算法對交通流時間序列進行分解，在分解過程中分解過程中，加入500組白噪聲信號，標準差為0.2。該算法的輸入數據是以5 min為時間間隔的交通流時間序列，輸出的是IMF分量。基于CEEMDAN分解的交通流各個序列如圖3所示。

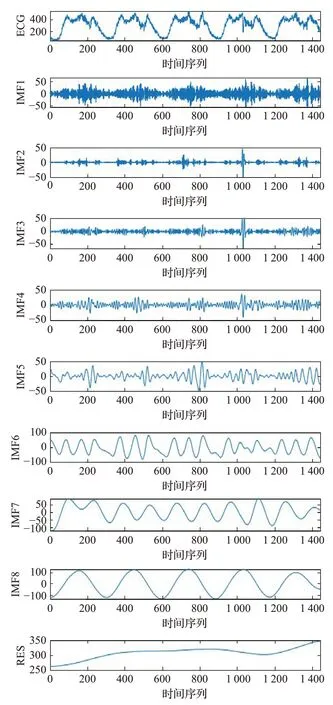
圖3 基于CEEMDAN分解的各個序列Fig.3 Each sequence based on CEEMDAN decomposition

為了減少計算規模，對分解后的各個時間序列分量進行隨機性分析，采用PE算法計算各個時間序列分量的排列熵，為了提高運算效率，將嵌入維數設置為m=6，延遲時間設置為t=3，通過Matlab計算得到各個時間序列分量的排列熵值，如表1所示，各個分量的標準化排列熵值的分布，如圖4所示。根據分解結果和排列熵值，分析各個時間序列分量的隨機性。從圖4和表1可以看出，IMF1的排列熵值最大，RES的排列熵值最小，隨著分量序列數的增加，排列熵值減小，表明時間序列分量的隨機性逐漸減弱。IMF1～IMF3分量具有較大的隨機性，列為高頻序列分量；IMF4～IMF6分量的隨機性一般，列為中頻序列分量；而IMF7、IMF8和RES分量的隨機性較弱，列為地頻序列分量，為后續混合預測模型的構建提供了依據。

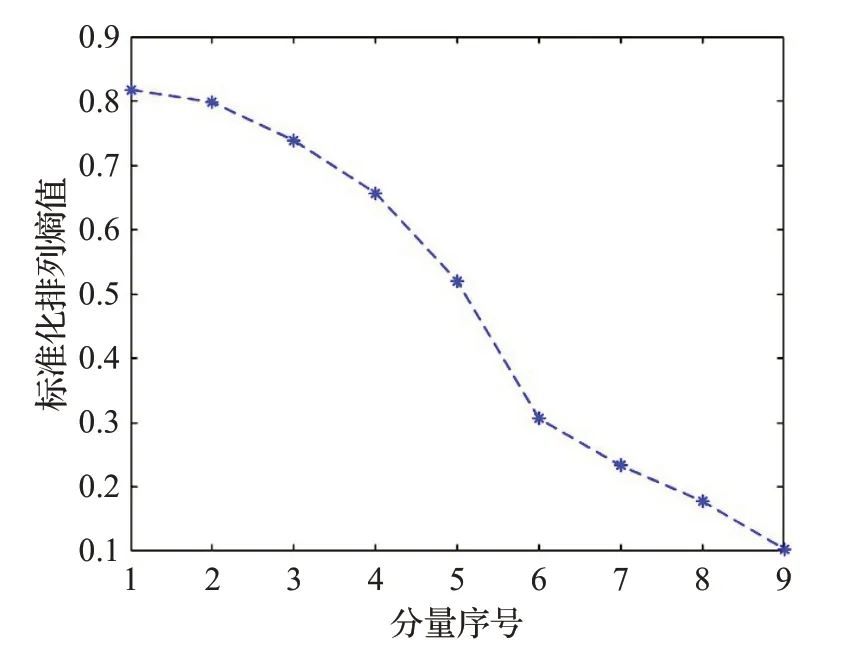
圖4 各個時間序列分量的標準化排列熵值分布圖Fig.4 Distribution diagram of normalized permutation entropy of each time series component

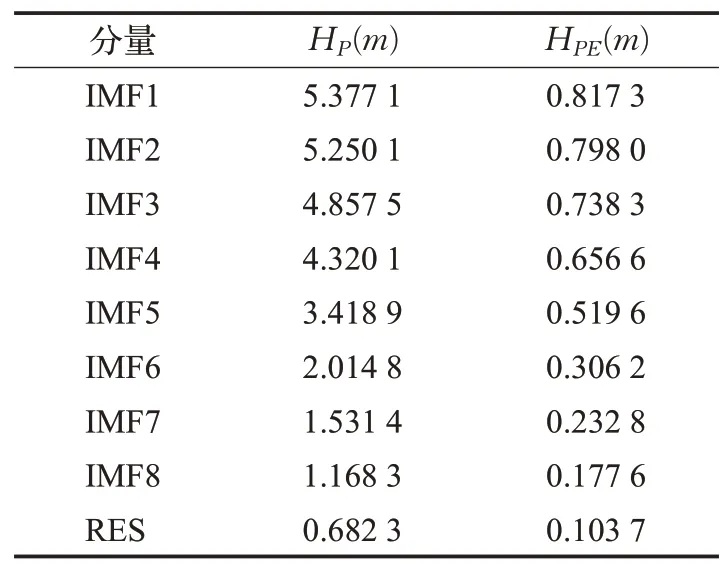
表1 各個時間序列分量的排列熵值Table 1 Permutation entropy of each time series component

3.3 基于CEEMDAN分解的短時交通流組合預測

針對交通流的高頻、中頻和低頻序列分量的特點分別建立GWO-BP模型、GWO-LSSVM模型和ARIMA模型進行預測。對于顯現較強非線性和隨機性的高頻序列分量IMF1～IMF3，采用GWO-BP模型進行預測；對于顯現一般非線性和隨機性的中頻序列分量IMF4～IMF6，采用GWO-LSSVM模型進行預測；對顯現較平穩的低頻序列分量IMF7、IMF8和RES，采用ARIMA模型進行預測。原始交通流時間序列基于CEEMDAN算法分解的9個分量預測結果如圖5所示。

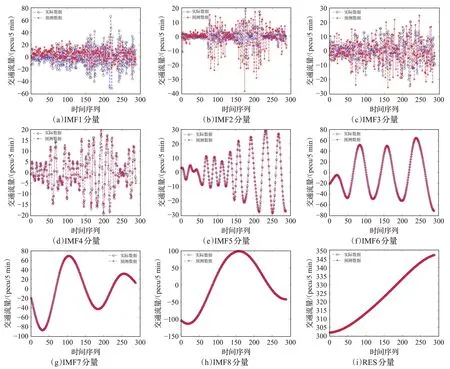
圖5 各分量預測結果曲線Fig.5 Forecast result curve of each component

預測評價指標是用來分析對比預測效果的，同時可以達到驗證模型的預測有效性的目的。本文采用均方根誤差（RMSE）和平均百分比誤差（MAPE）評價指標來評價模型預測結果。均方根誤差（RMSE）評價是用來評價觀測值和真實值的偏離程度，為了反映預測結果的離散程度以及預測精度。平均百分比誤差（MAPE）是用來評價整體預測結果與真實值的偏離程度，為了反映模型預測結果的好壞。評價指標公式如下：

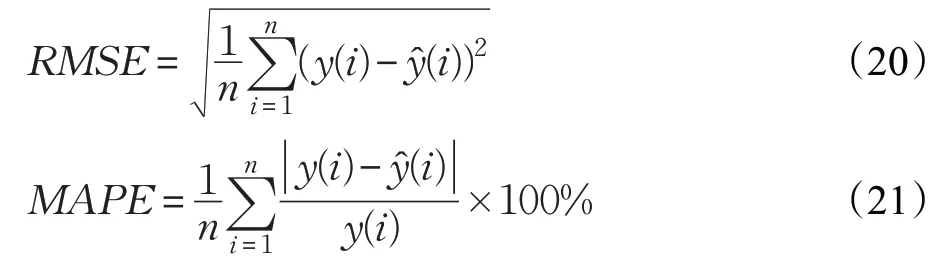
其中，y(i)表示i時刻的實際交通流量數據，y?(i)表示i時刻的預測交通流量數據，n表示預測樣本數量。RMSE和MAPE值越小表示模型預測誤差越小，預測效果越好。

為了驗證本文提出的預測模型的有效性，本文將基于CEEMDAN分解的短時交通流組合預測結果與采用ARIMA模型、BP模型、LSSVM模型及GWO-LSSVM模型的預測結果進行對比，如圖6所示。

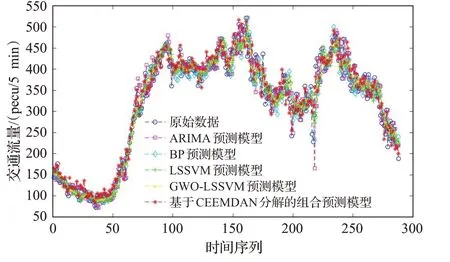
圖6 各預測模型預測結果與實際值比較Fig.6 Comparison of predicted results of each prediction model with actual value

基于CEEMDAN分解的組合預測模型與其他預測模型性能對比如表2所示。

由表2的2個交通流預測結果評價指標分析出，相比于其他4個預測模型，本文提出的基于CEEMDAN分解的短時交通流組合預測模型與交通流的真實值的擬合度最好。從表2可以看出，由于交通流隨機程度較大，ARIMA模型通常適用于平穩時間序列，因此采用ARIMA模型預測結果與交通流真實值的擬合程度最低。BP模型和LSSVM模型對交通流預測結果與真實值的擬合程度逐漸提高。與采用單一模型進行預測相比，采用組合預測方法，GWO-LSSVM模型對交通流真實值擬合程度進一步提升，但偏離程度仍然略高。本文提出的基于CEEMDAN分解的短時交通流組合預測模型，經過CEEMDAN序列分解，針對隨機程度不同的時間序列分量建立不同的預測模型，其預測結果明顯優于其他模型，預測誤差最小，均方根誤差RMSE為20.42，平均百分比誤差為5.8%。證明了所提出的組合預測模型有效地利用了ARIMA模型處理隨機性小的時間序列的優點，以及采用組合預測方法可以提高預測效果的特點。綜上所述，基于CEEMDAN分解的短時交通流組合預測模型能夠提升預測精度，具有良好的預測效果。

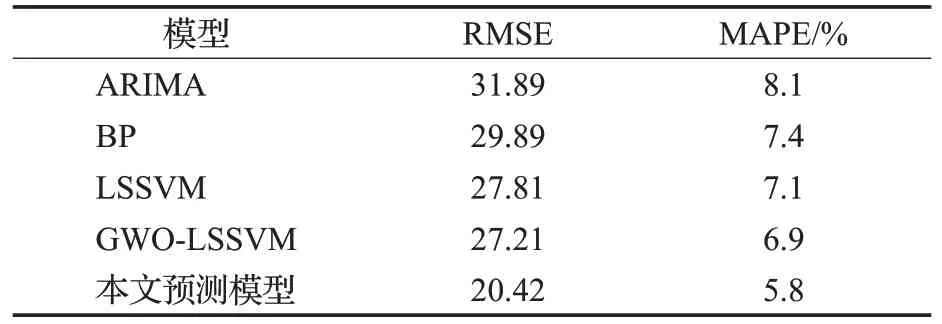
表2 預測模型性能對比Table 2 Performance comparison of prediction models

4 結束語

針對交通流數據具有非線性及隨機性的特點，本文提出基于CEEMDAN分解的短時交通流組合預測模型。首先利用CEEMDAN算法對交通流原始時間序列進行分解，其次，利用PE算法對分解后的各個交通流時間序列分量分析的隨機特性，根據時間序列分量的不同隨機特性分為高頻序列分量、中頻序列分量和低頻序列分量，根據高頻、中頻和低頻序列分量的隨機特性分別建立GWO-BP模型、GWO-LSSVM模型和ARIMA模型進行預測，疊加各個序列分量的預測結果，得到最終預測值。最后，通過采集的連續五個工作日的交通流進行仿真驗證，結果表明，本文提出的預測模型預測精度高于其他預測模型，在一定程度上提高了預測效果。但由于本文使用的交通流數據有限，且只考慮單一路段交通流預測，并未考慮其他路段的影響，將空間位置關系的影響加入交通流預測是本文下一步的研究方向。