堆積床相變蓄熱系統的傳熱特性研究

陳冬連 于程,* 張程賓 劉向東

1 東南大學能源與環境學院

2 揚州大學電氣與能源動力工程學院

1 前言

風能、太陽能等可再生能源對于實現“碳中和”具有重要意義，但可再生能源的間歇性和波動性問題對能源安全構成了威脅，而蓄熱技術利用蓄熱材料來存儲熱量實現能源削峰填谷、保障能源安全，受到了廣泛的關注[1-2]。其中相變蓄熱技術得益于較高的能量儲存密度具有較好的發展前景，但常用的相變材料（Phase Change Materials，PCM）導熱系數較低，制約了相變蓄熱技術的應用。為有效克服這一缺陷，研究人員采用堆積床方式構建相變蓄熱單元[3-4]。Regin 等[5]研究了以相變膠囊為基礎的堆積床相變蓄熱系統，發現可顯著提高蓄熱單元換熱速率。但堆積床相變蓄熱系統對堆積床內的耦合傳熱機理和堆積床相變蓄熱系統蓄熱性能的影響規律尚不清晰。

因此，本文建立勻速熱流條件下堆積床相變蓄熱系統非穩態傳熱模型，研究入口溫度對堆積床 PCM 的熔化行為演化特性和溫度分布特性的影響，從而為堆積床相變蓄熱系統的優化設計打下基礎。

2 模型的建立

2.1 物理模型

本文建立了一種堆積床相變蓄熱系統，其結構示意圖如圖1（a）所示。在堆積床中，傳熱流體從左側流入堆積床內，與膠囊顆粒發生對流換熱，而后從右側流出。另外，假設堆積床的外壁面有良好的保溫措施，是絕熱壁面。在堆積床中，膠囊顆粒的排布方式是有規律的，整個堆積床是由多個重復性單元在徑向和軸向堆疊而成的。

由于堆積床的每個單通道具有相同的流動傳熱特性，而單通道是關于 y、z 軸對稱的，為減少計算量，可進一步將計算模型簡化成1/4 單通道模型。為均勻速度分布和避免回流，在計算模型中堆積段的兩側分別增加入口段和出口段。本文的計算模型如圖1（b）所示，由入口段，堆積段及出口段等三部分構成，其中通道入口段 L1 長度為30 mm，堆積段 L2 長度為96 mm，出口段L3 長度為80 mm。為了保證顆粒能順利填充到通道內，顆粒直徑需要略小于通道截面尺寸。其中，顆粒的半徑尺寸為6 mm，通道截面寬度W的尺寸為6.1 mm，高度H的尺寸為6.1 mm。

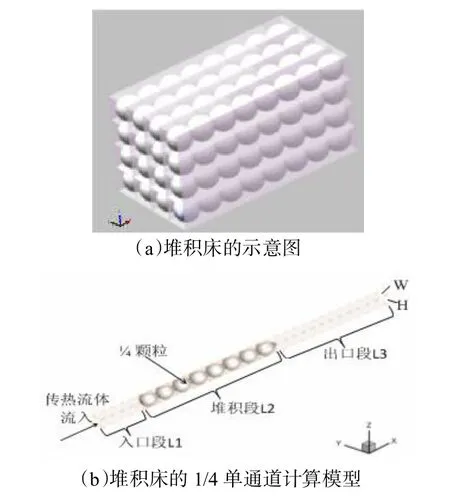
圖1 堆積床的結構示意圖

2.2 數學模型

為簡化 PCM 的熔化過程模型，本文主要做出了以下假設：1）假設堆積床的外壁為絕熱。2）PCM 的固相和液相性質是恒定不變的。3）忽略相變膠囊的厚度，假設膠囊內充滿相變材料。4）相變膠囊位置固定，無旋轉、移動、上浮或下沉的現象。

通過上述假設，可以得到簡化的連續性、動量和能量的方程：

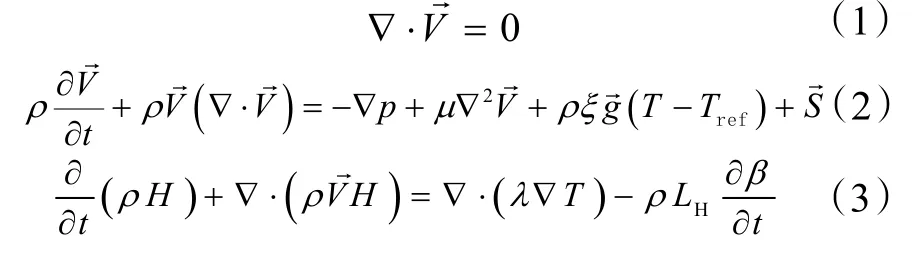
式中：V為速度矢量，ρ為密度，μ為動力粘度，ξ為熱膨脹系數，λ為導熱系數，t為時間，p為壓力，T為溫度，g為重力加速度，S為能量方程源項，LH是熔化的比熱潛熱，β是液相率，Tref為基準溫度，本文使用PCM 平均熔化溫度作為參考溫度。H為 PCM 的總焓值焓（H=h+ΔH）。

本文主要利用焓法模型模擬相變蓄熱堆積床里的 PCM 的熔化過程，分為三個階段：固體，液體和糊狀階段。引入了無量綱液體分數來計算PCM 在糊狀區域的熱特性，用溫度來表示：

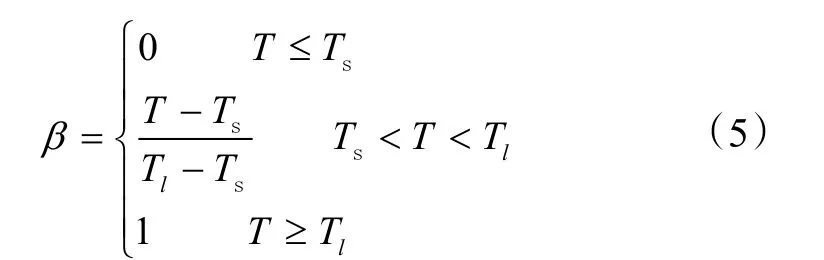
其中，下標l和S分別表示PCM 的液相線和固相線。利用由Carman-Koseny 方程導出的動量源項來修正PCM 在糊狀區液體流動，得到：

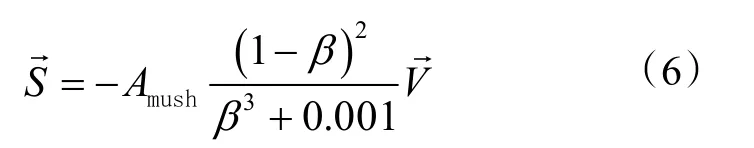
其中，Amush是糊狀區域常數，在105到108之間變化。由于較大的糊狀區常數更有利于得到準確的結果，本文糊狀區常數取108。

對于傳熱流體與相變膠囊外表面的對流換熱，進行簡化假設：1）傳熱流體的流動是非定常、不可壓縮的。2）傳熱流體性能不變。3）忽略粘滯散熱和體積力的影響。

本文中，堆積床的初始溫度為293 K，入口流體溫度為303 K。為保證入口流體為層流狀態，流體速度為0.1 m/s。相變膠囊選取PCM 材料為Paraffin-RT25，傳熱流體為液態水，具體的物性參數如表1 所示。

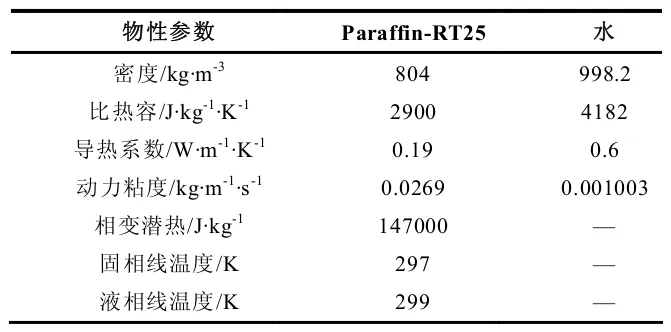
表1 PCM 和傳熱流體的物性參數

2.3 獨立性驗證

對于復雜物理過程的瞬態熔化過程，網格質量和時間步長選擇是兩個關鍵的參數設置。為了提高計算的收斂性，本文采用結構化網格。另外，采用不同網格尺寸進行網格獨立性檢測，確保本文數值計算解均為網格獨立的解。本文分別采用1164000，1708000 和2246000 這3 種網格和0.05 s、0.1 s、0.5 s 的時間步長，以完全熔化時間為指標進行了網格尺寸和時間步長獨立性檢測，結果表明當網格大于1708000 且時間步長為0.1 s 時，仿真結果為網格和時間步長獨立的解。為了節省時間消耗和計算資源，目前本文采用網格為1708000 和時間步長為0.1 s。

3 模擬結果與分析

3.1 PCM 熔化行為演化特性

圖2 給出了入口速度相同時，三種入口流體溫度下堆積床內PCM 液相率隨時間的變化。從圖中可見，溫度為303 K，308 K 和313 K 的堆積床 PCM 液相率分別在700 s、400 s、280 s 達到平衡狀態。入口傳熱流體溫度為313 K 的堆積床，相比較溫度為303 K、308 K 的堆積床，其熔化時間分別縮短了150.0%、42.9%。這主要由于傳熱流體與 PCM 的溫差增大、溫度梯度增大，使熱量更快從傳熱流體向相變膠囊傳遞，加快了 PCM 的熔化速率，從而堆積床的液相率變化更快。

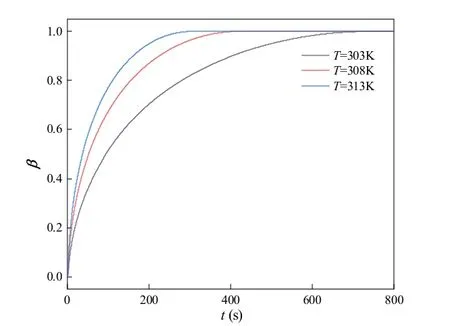
圖2 三種入口流體溫度下堆積床中 PCM 液相率隨時間的變化

圖3 給出了堆積床中相變膠囊位置和截面位置。這里需要指出的是，僅選擇沿流動方向的第六個相變膠囊顆粒，并取其垂直于流動方向的球體中心面及前后3 mm（膠囊半徑為6 mm）截面。圖4 展示了圖3 所示截面上的PCM 液相率分布云圖。可以看出，在堆積床中相變膠囊由外而內的逐漸熔化，溫度越高對應的 PCM 的液相越多。在280 s 時，溫度為313 K 的 PCM 基本熔化完全僅膠囊中心處有少量固態存在。溫度為308 K 的 PCM 有較小區域的固態存在。而溫度為313 K 的 PCM 卻有超過3 mm 范圍的大量固態存在。再次驗證了入口傳熱流體溫度越高，對應的堆積床內 PCM 的熔化行為越好。

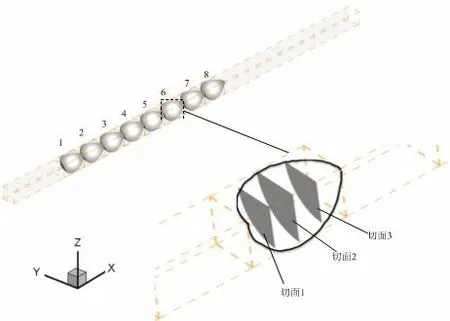
圖3 堆積床中相變膠囊位置和截面位置示意圖

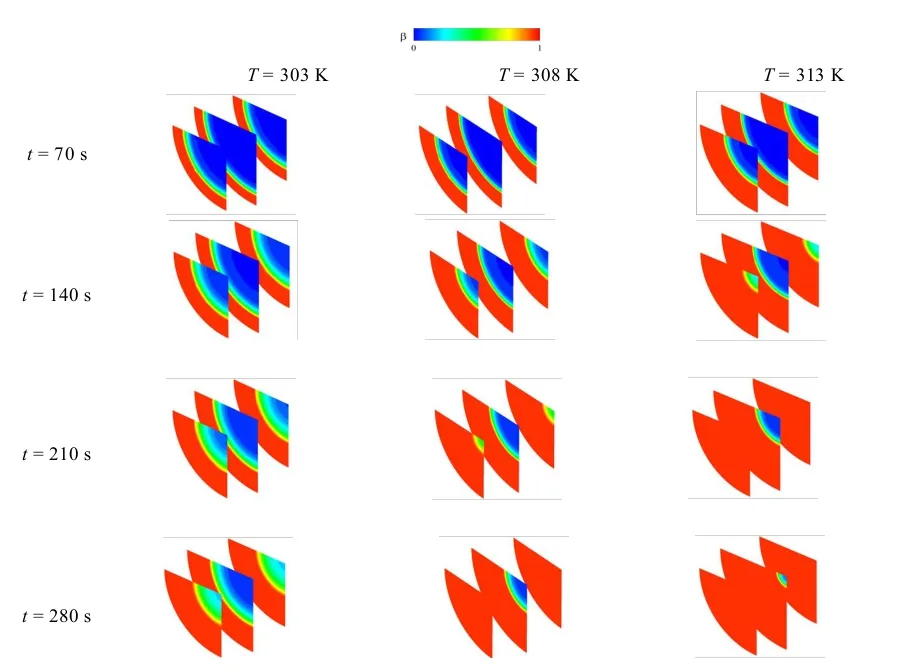
圖4 三種入口流體溫度下堆積床PCM 在不同時刻的液相率分布云圖

3.2 堆積床的溫度分布特性

圖5 給出了三種入口流體溫度下，相變膠囊內的溫度隨時間的變化。從圖可以看出，不同溫度下的 PCM 內的溫度曲線有明顯差異。這里需要指出的是，僅選擇沿流體流動方向的距離球心3 mm 處膠囊內的溫度。從單條溫度分布曲線可以識別出三個不同的階段：快速升溫階段（I），接著是恒溫階段（II），最后是幾乎線性的溫度升高階段（III）。

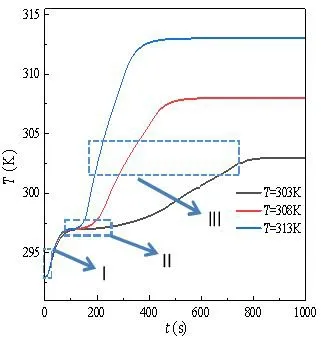
圖5 堆積床內膠囊溫度隨時間變化圖

從圖5 可以看出，I 區持續時間在0～80 s，是顯熱蓄熱階段，PCM 的溫度從初始溫度293 K 快速上升到相變溫度297 K。由于初始溫度與相變溫度相差較小，不同入口傳熱溫度對于該階段的區域長度影響較小。II 區持續的時間在80 到240 s，由于 PCM 的相變，其中熱量被 PCM 儲存為熔化潛熱，因此溫度保持恒定。該階段的持續時間取決于熔化潛熱值及換熱速率。相同的潛熱值下，換熱速率越大的堆積床在此階段所持續時間就越短。從圖可以看出，溫度為313 K，308 K 和303 K 對應的區域 II 持續的時間段分別為80～120 s、80～160 s、80～160 s。傳熱流體溫度越高，換熱速率越大，導致持續時間逐漸縮短。III 區與I 區相似，溫度線性上升是由于PCM 的顯熱蓄熱。PCM 溫度上升到傳熱流體入口溫度，堆積床的蓄熱達到一個平衡狀態。由于平衡溫度與 PCM 相變溫度相差較大，不同入口流體溫度對于該階段的溫度變化影響較大。

3.3 堆積床的蓄熱性能

高溫傳熱流體進入堆積床，與相變膠囊換熱將熱量傳遞后再流出堆積床。在熔化過程中，相變膠囊與傳熱流體的換熱是一個動態的過程，其總換熱量即可作為堆積床的蓄熱量。為了分析流體溫度對蓄熱性能的影響，圖6 給出了三種入口流體溫度下堆積床的蓄熱量隨時間的變化。從圖中可以看出，溫度為303 K、308 K、313 K 的堆積床蓄熱達到平衡狀態分別需要768 s、475 s、374 s。與入口流體溫度為303 K、308 K 的堆積床對比，溫度為313 K 達到最終熱平衡的時間分別縮短了105%、27 %。入口流體溫度的增加能明顯縮短堆積床的蓄熱時間，這主要由于高的傳熱溫差，使得熱量能以更快的速率從流體向PCM 中傳遞。另外，從圖中還可以看出，溫度為303 K、308 K、313 K 的堆積床在熔化過程中傳遞的熱量分別為994 J、1075 J、1157 J。與入口流體溫度為303 K、308 K 的堆積床對比，溫度為313 K 所儲存的熱量分別提高了16.39%、7.63%。在一定程度上，入口流體溫度的增加可以提高堆積床的蓄熱量。由于堆積床平衡溫度隨入口流體溫度增加而增加，使得 PCM 的顯熱蓄熱值增加，進而使得堆積床的總蓄熱量增加。

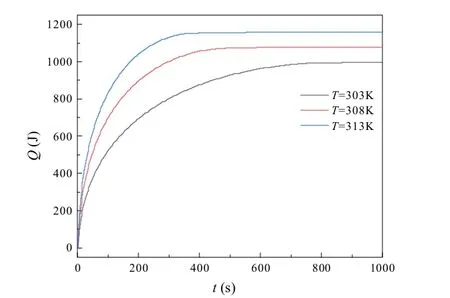
圖6 三種入口流體溫度下堆積床的蓄熱量隨時間的變化

4 結論

本文建立了勻速熱流條件下堆積床相變蓄熱系統非穩態傳熱模型，重點研究了不同入口流體溫度下 PCM 的熔化行為演化特性，溫度分布特性和蓄熱性能，主要得出以下幾點結論：

1）入口流體溫度的增加改善了堆積床的熔化性能。相同工況下，傳熱溫度為313 K 的堆積床與溫度為303 K 和308 K 的相比，PCM 完全熔化時間分別縮短了150.0%、42.9%。

2）同一初始溫度下，傳熱流體溫度對快速升溫階段和恒溫階段的PCM 溫度變化影響較小，對后期升溫階段的PCM 影響較大。

3）傳熱流體溫度的增加顯著加快了堆積床的蓄熱過程，且在一定程度上提高堆積床的蓄熱量。溫度為313 K 的堆積床與入口流體溫度為303 K、308 K 的相比，所達到最終熱平衡的時間分別縮短了105%、27 %，所儲存的熱量分別提高了16.39%、7.63%。