基于商空間粒度的序關(guān)系及其轉(zhuǎn)換研究
李海霞
(莆田學(xué)院 新工科產(chǎn)業(yè)學(xué)院,福建 莆田 351100)
0 引言
日常生活中人們時(shí)刻進(jìn)行著觀察、對(duì)比、決策.要進(jìn)行對(duì)比,首先要對(duì)事物按某種尺度進(jìn)行量化,在量化的基礎(chǔ)上排泛序[1]、求解問(wèn)題.對(duì)于比較復(fù)雜的問(wèn)題,在更小的細(xì)節(jié)上劃分的序(微觀序)下解決,會(huì)陷入細(xì)節(jié),難以求解,或者說(shuō)求解的復(fù)雜度比較高,這時(shí),需要進(jìn)行轉(zhuǎn)換,將微觀序轉(zhuǎn)化為更粗粒度上的序(宏觀序),在該序上解決問(wèn)題,可以降低求解問(wèn)題的復(fù)雜度,提高求解效率.
文章基于商空間粒度理論,討論了元素上的序(微觀序)到集合上的序(宏觀序)的轉(zhuǎn)換、集合上的序(微觀序)到集合冪集上的序(宏觀序)的轉(zhuǎn)換以及信息表上序的轉(zhuǎn)換,給出了微觀序到宏觀序轉(zhuǎn)換的步驟,并舉例說(shuō)明微觀序到宏觀序的轉(zhuǎn)換在人們生活中的應(yīng)用.
1 相關(guān)概念
1.1 商空間粒度理論
粒度(Granularity)[2-6]就是取不同大小的對(duì)象,是描述模糊和不確定性對(duì)象的工具.也就是說(shuō),將原來(lái)“粗粒度”的大對(duì)象分割成若干個(gè)“細(xì)粒度”的小對(duì)象,或者把原來(lái)若干個(gè)“細(xì)粒度”的小對(duì)象合并成一個(gè)粗粒度的大對(duì)象,進(jìn)行研究.我國(guó)學(xué)者張鈸院士曾經(jīng)指出:“人類智能的一個(gè)公認(rèn)的特點(diǎn):人們能從極不相同的粒度空間上觀察和分析同一問(wèn)題.人們不僅能在不同粒度世界上進(jìn)行問(wèn)題的求解,而且能夠很快地從一個(gè)粒度世界跳轉(zhuǎn)到另一個(gè)粒度世界,往返自如,毫無(wú)困難.這種處理不同粒度世界的能力,正是人類問(wèn)題求解的強(qiáng)有力的表現(xiàn)”[7].
在求解實(shí)際問(wèn)題的過(guò)程中,根據(jù)求解問(wèn)題的不同,需要不同粒度世界的描述.有時(shí)候解決同一問(wèn)題時(shí),同時(shí)需要若干不同粒度的世界.商空間理論[6-7]用三元組(X,f,T)描述一個(gè)問(wèn)題,其中X表示問(wèn)題的論域;f是論域的屬性,是對(duì)對(duì)象X的特征的刻劃;T是論域的結(jié)構(gòu),指論域X中各元素的相互關(guān)系(如距離、半序、拓?fù)涞?.分析或求解問(wèn)題(X,f,T),是指對(duì)論域X及其有關(guān)的結(jié)構(gòu)、屬性進(jìn)行分析、研究.比如,當(dāng)X很復(fù)雜時(shí),可以對(duì)X的大小粒度進(jìn)行簡(jiǎn)化,產(chǎn)生一個(gè)新的較大粒度的論域[X],那 么 把 原 問(wèn)題(X,f,T)變成新的層次上的問(wèn)題([X],[f],[T]).即從較粗粒度[X]去考察問(wèn)題.
1.2 商空間族的性質(zhì)
商空間族[7]即所有可能的商空間構(gòu)成的集合.
定義1給定一論域X,設(shè)R是X上一切等價(jià)關(guān)系的全體.定義R1,R2∈R,若x,y∈X,xR1y?xR2y,則稱R1比R2細(xì),記為R2 定義2給定X上的兩個(gè)拓?fù)銽1,T2,設(shè)Ti的全體開集構(gòu)成的集合族Oi,i=1,2.若O2是O1的子族,則稱T1比T2細(xì),記為T2 定義3設(shè)(X1,T1),(X2,T2)∈(X,T),若X1 定理1在(X,T)上定義如上的“<”關(guān)系,則(X,T)構(gòu)成一個(gè)完備半序格. 從不同粒度來(lái)考察問(wèn)題,所有可能選取的商空間和結(jié)構(gòu)就是(X,T)中的元素,文章主要討論對(duì)于給定的問(wèn)題,如何從(X,T)中選取更“粗”的元素進(jìn)行求解——將論域中的子集當(dāng)作新的元素進(jìn)行研究,用數(shù)學(xué)術(shù)語(yǔ)來(lái)講,就是對(duì)X進(jìn)行劃分,得到商集[X],然后對(duì)[X]進(jìn)行研究. 沒(méi)有什么東西是絕對(duì)微觀的或絕對(duì)宏觀的.采用微觀的觀點(diǎn)還是宏觀的觀點(diǎn)主要取決于觀察者的目的、理解和所處的環(huán)境等.不同的觀察者對(duì)相同的事物有不同的尺度[8],因此對(duì)于相同的事件,不同的觀察者會(huì)存在不同的觀點(diǎn)和不同的解決方法,即所謂的“橫看成嶺側(cè)成峰”. 泛系相對(duì)性[9-11]是指系統(tǒng)的相對(duì)性和關(guān)系的相對(duì)性,是形成宏觀序和微觀序的基礎(chǔ),宏觀和微觀不是絕對(duì)的,是相對(duì)的.根據(jù)泛系相對(duì)性,宏觀序是一般的序,而微觀序是從更小的細(xì)節(jié)上劃分的序.從粒度的觀點(diǎn)來(lái)看,宏觀序是在比微觀序更粗的粒度空間研究序. 由于解決問(wèn)題或決策的需要,經(jīng)常需要將微觀序轉(zhuǎn)換成宏觀序[12-13],在更粗的粒度空間解決問(wèn)題,以提高求解問(wèn)題的效率,降低求解問(wèn)題的復(fù)雜度. 如何將微觀序轉(zhuǎn)換成宏觀序呢? 結(jié)合1.2中商空間族的性質(zhì),接下來(lái)討論對(duì)于給定的問(wèn)題(微觀序下),如何通過(guò)商化,從(X,T)中選取合適的元素并定義宏觀序,以達(dá)到簡(jiǎn)化問(wèn)題的目的. 定義4集合A和B上定義序關(guān)系≤ ’: 滿足集合B中的元素或者大于集合A中的元素,或者與集合A中的元素沒(méi)有關(guān)系.將A、B上的這一關(guān)系記為g,則g= { 例1:設(shè)集合A= {a,b, 0, 1 },集合A上的序關(guān)系? = 圖1 集合A上的序關(guān)系f 眾所周知A= A的濾子:F= { 1,a}. A的理想:I= {b,0 }. 根據(jù)定義4,在F和I之間存在序關(guān)系≤′,將集合上的這一序關(guān)系記為g,則 g= { {F,I} ,≤′} = { < {0,b},{1,a} > }.如圖2所示. 圖2 { F,I }上的序關(guān)系g 序關(guān)系? 到序關(guān)系g的轉(zhuǎn)化如圖3所示. 圖3 序關(guān)系?到序關(guān)系g的轉(zhuǎn)換 顯然,序關(guān)系?= 從粒度的角度來(lái)看[4-5],微觀序?和宏觀序g是不同的粒度層次,宏觀序g是更粗的粒度空間上的序.在更粗粒度空間上解決問(wèn)題,能降低求解能提的復(fù)雜度. 定義5設(shè)A是一個(gè)集合,A的子集B?P(A)(P(A)是集合A的冪集合),B= {B1,B2,B3, …},對(duì)于任何X∈Bi如果存在集合Y, 并且滿足Y∈Bj,X?Y,則Bi?Bj. 例2:設(shè)集合A= {{a,b,c,d},{a,c},{a,b}, {a}},集合A上的序關(guān)系?′= 圖4 集合A上的序關(guān)系?′ 構(gòu)造滿足定義5的集合B,B={{{a,b,c,d}},{{a,c},{a,b}},{{a}}},則B上有包含關(guān)系?′,集合B和B上的包含關(guān)系?′形成序關(guān)系g′= 圖5 集合B上的序關(guān)系g′ 序關(guān)系?′到序關(guān)系g′的轉(zhuǎn)換如圖6所示. 圖6 集合上的序到集合的冪集上的序的轉(zhuǎn)換 容易得知,序關(guān)系?′= 同樣地,從粒度的角度[4-5]來(lái)看,微觀序?′和宏觀序g′是不同的粒度層次,宏觀序g′是更粗粒度空間上的序.在更粗粒度空間上解決問(wèn)題,能降低求解能提的復(fù)雜度. 信息表是粗糙集理論中對(duì)知識(shí)進(jìn)行表達(dá)和處理的基本工具.信息表與泛權(quán)場(chǎng)一一對(duì)應(yīng),故可以將信息表的研究轉(zhuǎn)變?yōu)閷?duì)泛權(quán)場(chǎng)的研究. 經(jīng)典粗糙集理論中,論域U是元素的集合,未能顯化事物和事物的區(qū)別,所以對(duì)事物的認(rèn)識(shí)不是很清晰.為此,引入了元素語(yǔ)義,構(gòu)成泛權(quán)場(chǎng),泛權(quán)場(chǎng)顯化了事物之間的區(qū)別,使得對(duì)事物的描述更全面,對(duì)事物的認(rèn)識(shí)更清晰. 定義6泛權(quán)場(chǎng)[1]:在一個(gè)廣義系統(tǒng)S=(A,B)中,如果滿足B:A→W,則S就是一個(gè)泛權(quán)場(chǎng),其中W為A的泛權(quán)集. 定義7子泛權(quán)場(chǎng):設(shè)泛權(quán)場(chǎng)fU:U→W,fX:X→W,集合X?U,如果對(duì)?x∈X,不存在y∈U-X,使得fX(x)=fU(y),稱fX是fU的子泛權(quán)場(chǎng). 特別地,設(shè)? 也是fU的子泛權(quán)場(chǎng). 定義8偏序“?”(“?”)上的宏觀序“?*”(“?*”):設(shè)fX、fY∈P(B),?fx∈fX和?fy∈fY要么fx?fy(fx?fy)或fx,fy沒(méi)有“?”關(guān)系,則有fX?*fY(fX?*fY).其中B為某泛權(quán)場(chǎng)所有子泛權(quán)場(chǎng)的集合;P(B)為B的冪集. 例3:假設(shè)有如圖7所示的泛權(quán)場(chǎng)布爾代數(shù): 圖7 某泛權(quán)場(chǎng)布爾代數(shù) 根據(jù)定義8,對(duì)圖7某泛權(quán)場(chǎng)布爾代數(shù)進(jìn)行商化,如圖8所示. 圖8 某泛權(quán)場(chǎng)布爾代數(shù)的商化 商化后得到如圖9所示的商化后的序. 圖9 商化后的序 在此基礎(chǔ)上,根據(jù)定義8,對(duì)圖9中的序繼續(xù)商化,如圖10所示. 圖10 對(duì)商化后的序的商化 構(gòu)造出更粗粒度空間上的宏觀序(線型序),如圖11所示. 圖11 商化后的宏觀序(線型序) 在這里,將原來(lái)的泛權(quán)場(chǎng)布爾代數(shù)通過(guò)求商、再求商,最終變成了線形序.大大降低了問(wèn)題的復(fù)雜性. 定理2任何一個(gè)泛權(quán)場(chǎng)布爾代數(shù),通過(guò)商化,最終可轉(zhuǎn)變?yōu)榫€形序. 定理3商化之后的偏序或線形序中,最小元為原布爾代數(shù)的理想,最大元為原布爾代數(shù)的濾子.商化越厲害,對(duì)應(yīng)的理想和濾子也越大. 為了提高問(wèn)題的求解效率,降低求解問(wèn)題的復(fù)雜度或者決策的需要,經(jīng)常需要結(jié)合商空間粒度理論將微觀序轉(zhuǎn)換為宏觀序,在更粗的粒度空間分析、解決問(wèn)題.具體轉(zhuǎn)換步驟如下: Step 1 分析研究當(dāng)前微觀序的元素和元素上的序關(guān)系(微觀序); Step 2 根據(jù)1.2商空間族的性質(zhì),在微觀序的基礎(chǔ)上構(gòu)造更粗的粒度空間——將論域中的子集當(dāng)作新的元素進(jìn)行研究; Step 3 定義出粗粒度空間上的序關(guān)系(宏觀序). Step 4 如有需要,再重復(fù)step1、step2、step3步,構(gòu)造出更粗粒度空間上的序. 微觀序從更細(xì)節(jié)的地方觀察和控制事物,而宏觀序從整體上、全局上觀察和控制事物.下面舉一個(gè)日常生活中微觀序到宏觀序轉(zhuǎn)換的簡(jiǎn)單例子. 例:升學(xué)考試過(guò)程:學(xué)生考試,獲得分?jǐn)?shù);學(xué)校根據(jù)招生人數(shù)、學(xué)生分?jǐn)?shù)高低以及排名,決定是否錄取. 考試是量化學(xué)生學(xué)習(xí)好壞的一個(gè)工具,考得的分?jǐn)?shù)是量化的結(jié)果.通常情況下,按照學(xué)生分?jǐn)?shù)的高低排名(圖12左),這是學(xué)生及家長(zhǎng)所關(guān)注的;對(duì)老師來(lái)說(shuō),更關(guān)注學(xué)生在各個(gè)分?jǐn)?shù)段的分布情況(圖12中);而對(duì)升學(xué)來(lái)說(shuō),只關(guān)注哪些學(xué)生被錄取(圖12右). 圖12左邊的序關(guān)系是微觀序,不適合做決策.對(duì)于學(xué)校來(lái)說(shuō),他們只需要確定一個(gè)升學(xué)的錄取分,如果考生的成績(jī)高于錄取分,則錄取,否則,不予錄取. 圖12 微觀序到宏觀序的轉(zhuǎn)換 可以看出,對(duì)于決策者學(xué)校來(lái)說(shuō),從宏觀序進(jìn)行升學(xué)錄取的效率更高. 人們?cè)谖⒂^序下,分析問(wèn)題、解決問(wèn)題的效率不高,經(jīng)常需要從微觀序轉(zhuǎn)換到宏觀序,從宏觀上做決策. 文章結(jié)合商空間粒度理論,重點(diǎn)討論了元素上的序到集合上的序的轉(zhuǎn)換、集合上的序到集合冪集上的序的轉(zhuǎn)換以及信息表上序的轉(zhuǎn)換,給出了微觀序到宏觀序轉(zhuǎn)換的步驟,并舉例說(shuō)明微觀序到宏觀序的轉(zhuǎn)換在人們生活中的應(yīng)用. 通過(guò)將微觀序轉(zhuǎn)換為宏觀序,對(duì)復(fù)雜問(wèn)題進(jìn)行更粗的粒度劃分, 將其轉(zhuǎn)化成較為簡(jiǎn)單的問(wèn)題, 從而有助于對(duì)復(fù)雜問(wèn)題的分析與求解.1.3 微觀序和宏觀序
2 微觀序到宏觀序的轉(zhuǎn)換
2.1 元素上的序到集合上的序的轉(zhuǎn)換
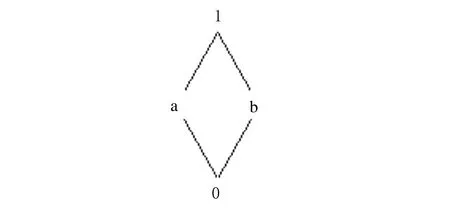
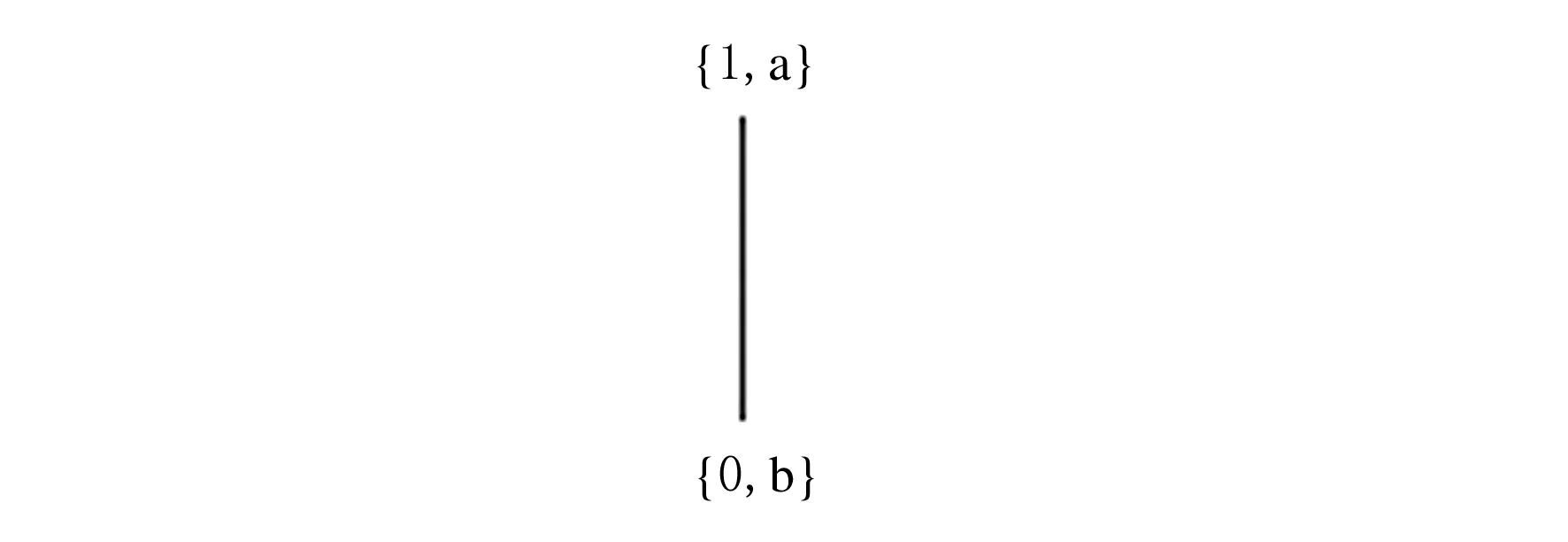
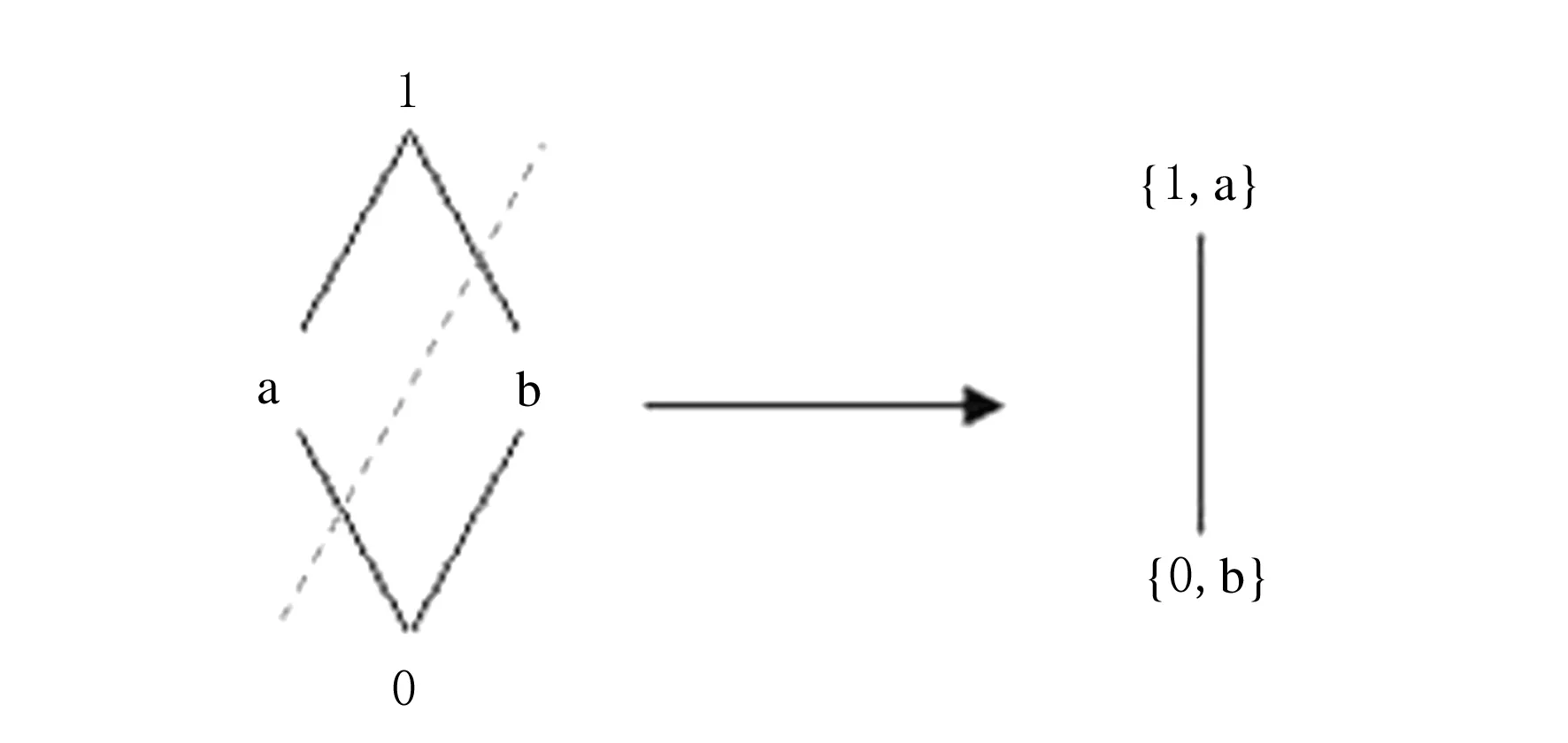
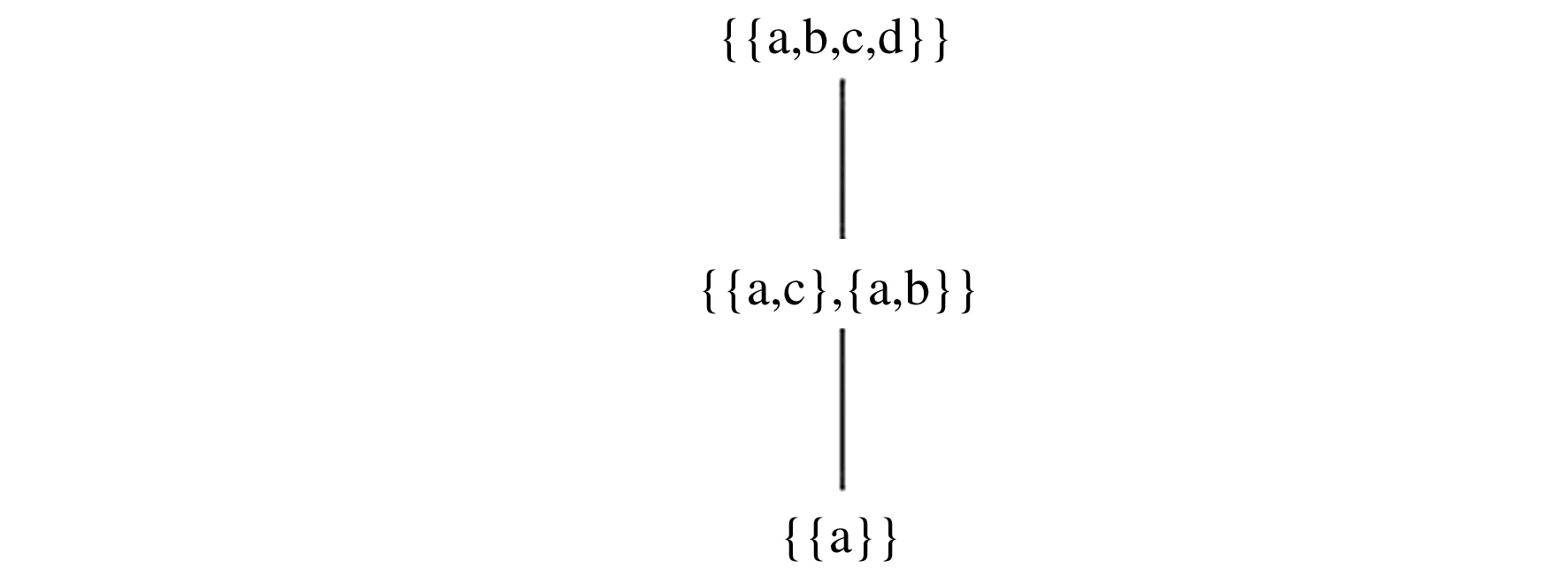
2.2 集合上的序到集合冪集上的序的轉(zhuǎn)換
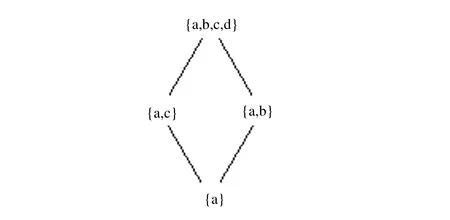

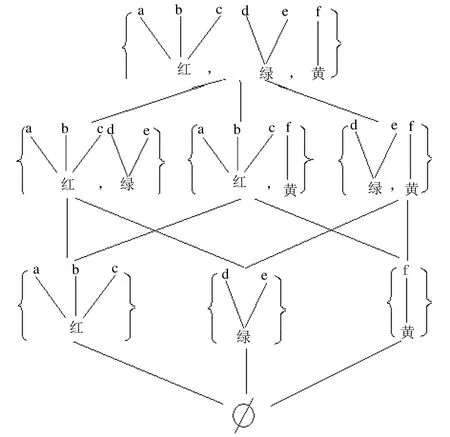
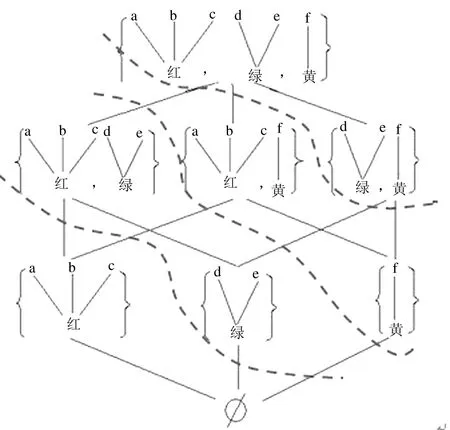
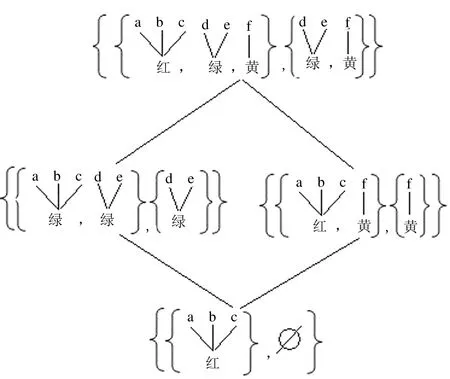
2.3 信息表上序的轉(zhuǎn)換
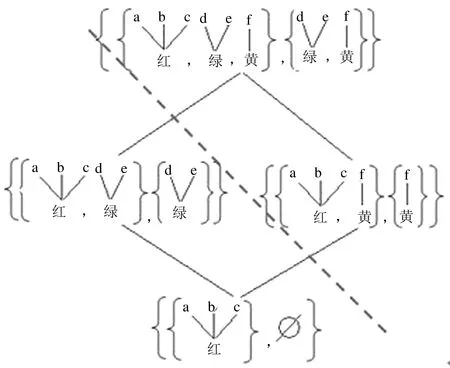
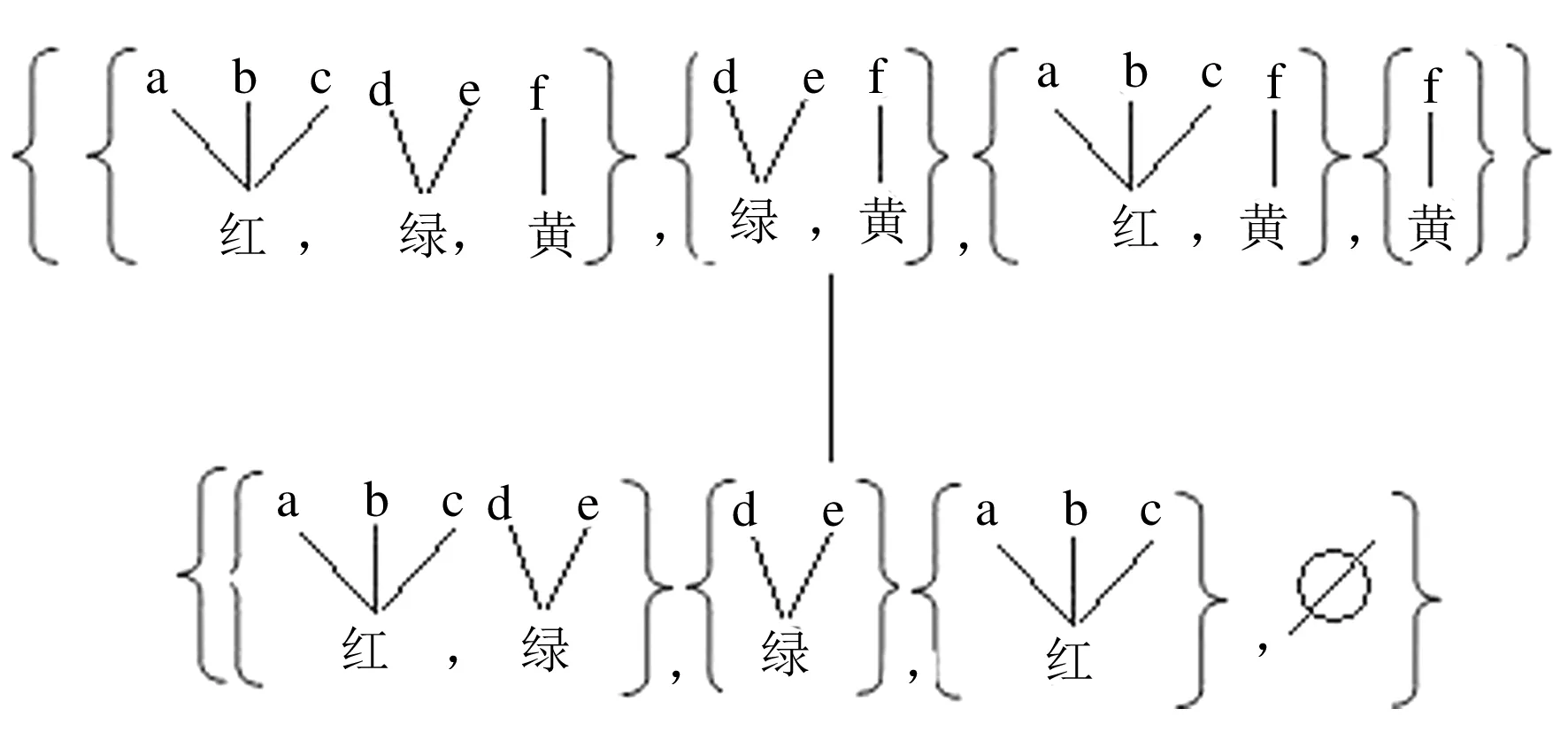
2.4 從微觀序到宏觀序轉(zhuǎn)換的方法
2.5 從微觀序到宏觀序轉(zhuǎn)換的應(yīng)用
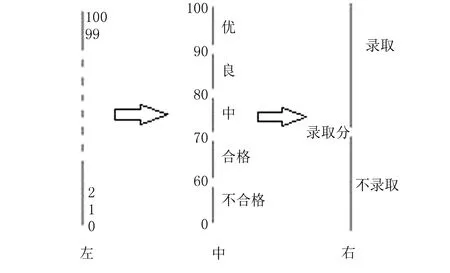
3 結(jié)語(yǔ)

