圍繞知識“生成”　提高課堂實效——以《等差數列的前n項和》為例

顧維維

圍繞知識“生成”提高課堂實效——以《等差數列的前項和》為例

顧維維

（江蘇省蘇州市吳中區木瀆金山高級中學，江蘇蘇州215128）

課堂教學是學生知識生成、思想鍛煉、技能習得的主陣地，圍繞知識“生成”，關注過程性教學，讓學生“親”經歷“真”思考，參與其中又“樂”在其中，提高課堂教學實效。

等差數列；首尾配對

高效課堂教學的一個重要特點是在教與學的過程中讓知識真實、自然地生成，對關鍵問題的細節設計往往是“成敗”的關鍵。筆者通過聽課學習有感而發，結合自身教學實踐，以《等差數列前n項和》為載體，闡述教學應如何圍繞知識生成而設計，進而從根本上提高課堂實效。

一、問題的提出

二、教學問題診斷與策略

如何讓“倒序相加”的思想在學生腦海里自然生成？首先高斯算法需要“配對”，當項數不定時，就要討論項數的奇偶性，討論起來就比較煩瑣，是否有簡便的算法成為客觀需求，這是需求鋪墊。其次，通過問題情境建立數學模型，設置問題1和問題2及其變式，讓學生深刻理解高斯算法的關鍵就是“配對”以及具體如何配對。這是知識與技能鋪墊。最后借助問題情境中“三角形數”模型的幾何直觀，同時結合“數的首尾配對”，學生容易想到“形的首尾配對”，即圖形的“倒置、拼補”思想萌芽就自然形成了，從“數”與“形”兩個角度突破難點。

三、教學過程

（一）創設情境，提出問題

傳說古希臘畢達哥拉斯學派的數學家經常在沙灘研究數學問題，他們在沙灘上畫點或用小石子表示數。一定數目的點或圓在等距離的排列下可以形成一個等邊三角形，這樣的數被稱為“三角形數”，如下圖所示。

那么第100堆的石子數是多少？

教師：這個題目蘊含了哪些我們前面學過的知識？請同學們回憶一下。

教師：第100堆的石子數是多少呢？

學生：第100堆有100層，若記最上面一層為第1層，那么第1層1個，第2層2個，第3層3個……第100層是100個，所以第100堆的石子數是1+2+3+4+……+98+99+100=？

教師：觀察這組數的求和有什么特點？

學生：這是一個首項和公差都是1的等差數列的前100項之和。

設計意圖：第一，對于“三角形數”模型，學生在前面學習數列的通項公式時已學習，使得學生能夠快速抓住關鍵問題，引出本節所要解決的問題。同時結合教師引導，學生能夠內化前面學的等差數列的相關概念。第二，“三角形數”模型是本節課的主要載體，貫穿于整個課堂教學活動。第三，模型本身拉近了與學生之間的距離，營造了輕松的學習氛圍，體現了情境引入的人文價值和應用價值。

（二）探索質詢，追根溯源

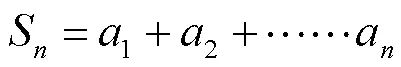
情境中的所求問題可以表示為：

教師：怎樣快速求出其和？

學生：考慮“首尾配對”，1+100=2+99=3+98=……=50+51。

教師：漂亮！你的想法很有創意，計算起來非常簡便。

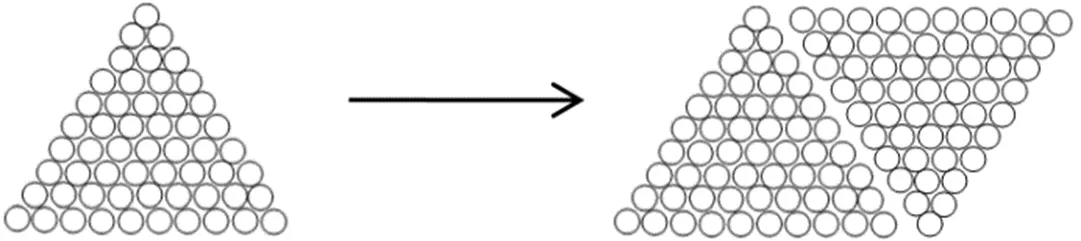
巧合的是，德國著名數學高斯在他10歲的時候就解決了這樣一個問題，和這位同學想法一致，通過對應首尾配對，將不同數的求和問題轉化為相同數的求和問題，即100=1＋2＋3＋……＋100＝（1＋100）＋（2＋99）＋……＋（50+51）＝101×50＝5050.

教師：這種解法非常好，但是有沒有什么弊端？

學生：不是都能配對的，比如項的個數是奇數個。

教師：很好！請同學們看問題2。

問題2：計算99=1+2+……+99的值。

教師：此時又如何解決呢？

學生1：99＝（1+2+……+99+100）－100=100－100＝4950。

教師：厲害！通過加一項減一項實現部分配對，化奇為偶，從而找到“相同數”，有沒有其他解法了呢？

學生2：99=（1＋2＋……＋98）＋99＝98＋99＝99×49＋99＝4950。

學生3：99=1＋（2＋……＋99）＝1＋101×49＝4950。

學生4：99＝（0+99）＋（1＋98）＋……＋（49＋50）＝99×50＝4950。

設計意圖：首先給出一個連續偶數項和的求和，理解首尾配對求和的原理和方法，然后通過問題2引導學生對連續奇數項和的求解問題的思考，進而更深層次地理解高斯求和的精髓和局限性，為后面倒序相加法的使用做出鋪墊。

問題3：以上我們僅僅是從數的角度構造“首尾配對”進行研究，請同學們回到問題情境中去，能否從其他角度考慮問題1呢？（小組合作討論）

小組代表：對圖形也進行“首尾配對”。

教師：你能畫出草圖嗎？

學生展示。

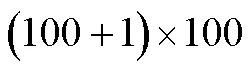
設計意圖：高斯算法需要“配對”，當項數不定時，那么就要討論項數的奇偶性。為了改進算法的同時引出倒序相加原理就設置了問題3，前面研究的“首尾配對”求和是從數的角度，借助情境中的幾何模型求和的。此時學生容易想到從“形”的角度考慮“圖形首尾配對”，即圖形的“倒置、拼補”思想萌芽就自然形成了。緊接著，學生經過小組合作探究，動手試驗，畫出草圖，得出結果。

問題4：如果將問題1中的100改為n，請計算S=1＋2＋3＋……＋.

教師：比一比誰算得既快又準。

教師：很好，那么對上述解法，如何用數學語言表示出來？

兩式相加，得2S＝（＋1）＋（＋1）+……+（+1）＝（+1）

教師：這種算法妙在哪里？你能給它起個名字嗎？

學生：不用考慮項數的奇偶問題，“首尾配對相加法。”

教師：很好，抓住了本質！

上述解法可以總結為兩步：首先倒序表示出S，然后兩式相加，所以在數學上稱這種解法為倒序相加法。

設計意圖：①根據問題3的討論，學生容易想到通過倒置配對，拼補成平行四邊形解決，強化學生對倒序相加法理解和運用；②避開了對項數奇偶的討論，使得教學活動更加緊湊連貫，學習目標更加清晰明確；③引導學生由圖形語言——數學語言——符號語言的轉化，培養學生的數學抽象和邏輯推理的數學素養。

教師：前面我們研究了100，S，都是從1開始加起來，能從其他數開始嗎？

問題5：根據問題情境，從第4行到第n行共有多少個石子？（小組合作探究并畫出草圖）

教師：都很棒，前面同學利用問題4的方法，將“梯形倒置”轉化為平行四邊形處理，后面同學使用“分割”手段，整體減去部分，在問題1結論的基礎上計算，兩種解法答案化簡后是一致的，可謂“殊途同歸”！（幾何畫板動態展示，如下圖所示）

設計意圖：由三角形倒置拼補，類比研究梯形倒置拼補，進一步強化學生對倒序相加法原理的理解和運用，為后面等差數列求和公式的推導奠定了基礎。

（三）自主探究，匯報交流

S＝1＋2＋3＋……＋a-2＋a-1＋a

S＝a＋a-1＋a-2＋……＋3＋2＋1

兩式相加得，2S=（1＋a）＋（2＋a－1）＋……＋（a＋1）=（a＋1）

S＝1＋2＋3＋……＋a=1＋（1＋）＋（1＋2）＋……＋[1＋（－1）]

S＝a＋a－1＋……＋1=a＋（a－）＋（a－2）＋……＋[a－（－1）]

兩式相加得2S＝（1＋a）＋（1＋a）＋（1＋a）＋……＋（1＋a）＝（1＋a）

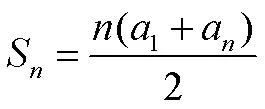
S＝1＋（1＋d）＋（1＋2d）＋……[1＋（－1）]

＝1＋[1＋2＋……（－1）]

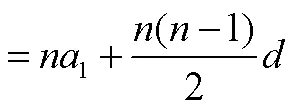
教師：（1）公式一和公式二是否相等？請給出嚴格證明；

（2）這兩個公式中共包含哪些量？如何選取合適公式進行計算？

設計意圖：從問題3到問題5，讓學生經歷特殊——一般——再一般的探究過程。基于上述活動經驗的積累，學生對問題6等差數列求和公式的推導變得水到渠成。在這個過程中放手讓學生自主推導，并交流成果，使學生對倒序相加法認識得到了進一步的升華。

四、反思與感悟

（一）以教材為方向，用“好”教材，精心設計問題情境

筆者參閱了各個版本的教材，深刻挖掘教材中所給情境的內涵，以及它們之間的區別和聯系，認為問題情境的創設應“源于課本，高于課本”，一般應遵循適用性、目的性、科學性和趣味性原則。本文創設的問題情境是從學生熟悉的“三角形數”入手，引出“高斯算法”，讓學生理解其“配對”思想，為后面問題1和問題2的研究做了較好知識準備；同時借助“三角形數”模型的幾何直觀，為后面問題4、5、6的研究做了思想、方法準備，貫穿于整個教學活動之中。

（二）以問題為主線，遵循知識生成、發展規律

教學活動的設計是基于“人”為前提，設計是“為人服務”的，應遵循知識生成方式和發展的規律。尤其在重難點處的設計應充分以學生為中心，站在學生的角度看待問題，想學生之所想，解學生之所惑。如何讓“倒序相加”的思想在學生腦海里自然生成？這就是本節課的難點，教學設計以問題串線貫穿始終，從問題情境到問題1，從問題1到問題6，始終秉持以自主探究、動手實驗、合作交流、成果展示、“查缺補漏”的方式讓學生參與進來，問題設置上層層遞進，分散問題難度，將重難點逐步“瓦解”。

（三）以重視“過程性教學”為原則，建構高效教學活動

《普通高中數學課程標準（2017年版）》明確提出學習評價既要關注學習結果，更要重視學生學習過程。過程性教學的關鍵是要創造合適的條件將學生“融入”到教學活動上來，讓學“親經歷，真思考”。比如在前面問題探討時，學生會遇到不定項數連續等差數列求和時該怎么辦，是硬著頭皮分類討論算下去，還是“另尋出路”？教師應留有一定時間讓學生經歷這樣一個思維過程，而不是直接或間接說出結果，再或者“逼著”學生往這個結果上引導。本文適時給出了問題3，讓學生主動發現可以從“數”和“形”兩個角度同時考慮，此時的學生有了一種“恍然大悟”。有了這種思想萌芽，緊接著讓學生思考、試驗，然后交流成果。讓學生真實經歷了這樣一個自主探究的完整過程，從根本上提高了課堂教學的有效性。

[1] 中華人民共和國教育部.普通高中數學課程標準(2017年版)[M].北京:人民教育出版社,2018.

G632

A

1002-7661(2022)10-0135-03