轉化思想在初中數學建模教學中的應用
梁燕冰(廣東省佛山市南海區(qū)獅山鎮(zhèn)羅村第二初級中學)
數學建模的過程是“分析問題—合理假設—分析模型—找到方法—建構模型—檢驗模型—解決問題”。培養(yǎng)學生的數學建模能力是教師的重要任務之一,然而提起數學建模,很多學生不知道其中的內涵,更不用說掌握建模的方法。下面,筆者談談如何將數學建模問題歸類與轉化成學生熟悉的、易懂的數學問題,從而更好地幫助學生理解數學建模并掌握相關方法。
一、轉化為方程問題的數學建模
方程是指含有未知數的等式。在對實際問題建模的過程中會經常涉及一些等量關系,此時可以在數學建模中構建方程模型。
例1 現有兩塊大小相同的長方體木板,用它們來測量桌子的高度,如圖1 放置并測量數據,然后改變木板的放置方法;如圖2 放置并測量數據,試計算桌子的高度。
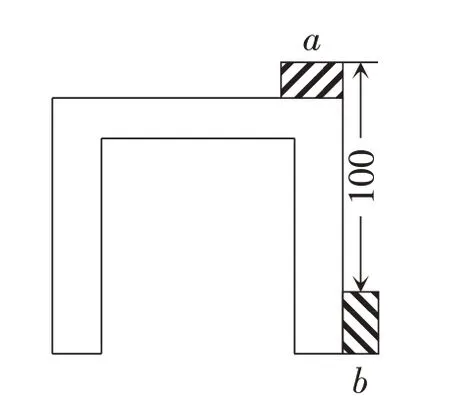
圖1
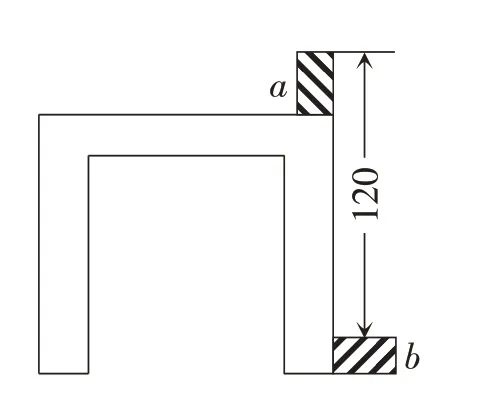
圖2
教師引導學生先假設木塊的長、寬和桌子的高度,然后讓學生小組討論并匯報。
解:設木塊的長為acm,寬為bcm,桌子的高為xcm,
依題意,得b+x-a=100,a+x-b=120。
兩式相加,消元求出x=110。因此,桌子的高度為110 cm。
【反思】經過師生共同探討,學生感受到了什么是數學建模,也體會到了求解成功的喜悅。同時,通過例題教師還總結了在生活中測量桌子高度的方法,讓學生感受到了學以致用的樂趣。
二、轉化為幾何問題的數學建模
幾何與人類的生活密切相關。實際生活中的數學建模問題,尤其涉及角度問題時,需要轉化為常見的幾何問題,利用銳角三角函數、勾股定理等知識進行求解。
例2如圖3,有一把搭在墻上的梯子長4 m,其與地面所成的角度為45°。當把它調整為與地面成60°角時,求梯子的頂端沿墻面上升了多少。

圖3
教師指導學生把梯子的兩種擺放情況簡明地畫出來(如圖4),然后師生一起分析并完成解題過程。
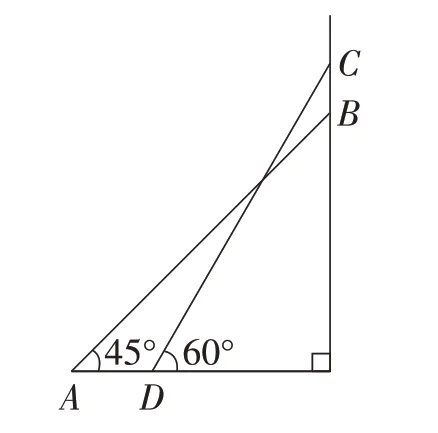
圖4
解:梯子的頂端沿墻面上升的高度為BC=
【反思】教師引導學生依據題設畫出幾何圖形,把題目中看似不容易表示的“梯子的頂端沿墻面上升了多少”等價轉化為“求線段BC的長度”,化繁為簡。此題是學生在學習三角函數時的常見題型,計算過程不復雜,重在讓學生學會把生活中的一些數學建模問題用幾何圖示分析并求解,讓學生不再認為數學學習枯燥。
三、轉化為不等式相關的數學建模
對于生產決策、購買方案、統(tǒng)籌安排等現實生活中的問題,可以通過分析數據,然后轉化為不等式進行計算解決。
例3班主任讓小明和小紅用70 元獎勵金去購買鋼筆和筆記本共20件,獎勵平時表現突出的學生。已知鋼筆每支5元,筆記本每本1元,班主任要求鋼筆的數量不少于筆記本的數量,共有多少種購買方案?
教師先引導學生理解題意,并提醒學生注意取值范圍的限制,然后師生共同完成解答過程。
解:設購買筆記本x本,依題意,得

教師引導學生根據實際情況取整并檢驗,得出共有3 種購買方案:鋼筆12 支,筆記本8 本;或者鋼筆11支,筆記本9本;或者鋼筆10支,筆記本10本。
【反思】涉及方案的建模題目對于很多學生來說都比較困難。此例題中,教師引導學生把題目中的兩個條件“購買金額不超過70元”和“鋼筆的數量不少于筆記本的數量”直接轉化為不等式,列出不等式組來求解,而取整數其實就是對模型的檢驗。此題讓學生經歷了數學建模的整個過程,不僅讓學生體會了數學建模的含義,還讓學生對數學的學習更有興趣和信心。
四、轉化為函數問題的數學建模
在現實生活中,最大獲利、成本最低等問題可以嘗試構建函數模型來求解。
例4某養(yǎng)豬場若每天投入3.2 元,則可讓一頭60 kg重的生豬每天增加2 kg。已知當時生豬的市場價格為每千克20元,但同時估計每天每千克生豬價格下降0.4 元。對于該養(yǎng)豬場而言,當時60 kg 重的生豬在什么時候出售可以獲得最大利潤。
解:設在t天后出售生豬,養(yǎng)豬場能獲得最大利潤,此時養(yǎng)豬場的投入為3.2t元,每頭生豬能賣( 20-0.4t)( 6 0+2t)元,最大利潤為( 2 0-0.4t)( 6 0+2t)-3.2t=1 200+40t-24t-0.8t2-3.2t= -0.8t2+12.8t+1 200=-0.8(t2-16t)+1 200= -0.8(t-8)2+1 251.2。所以,在8 天后賣出生豬,可以獲得最大利潤。
【反思】此題是一道關于二次函數的最值問題,教學時應該引導學生配方,根據實際情況來檢驗答案的合理性。此題中,經過8 天后,雖然后來投入是8 ×3.2=25.6(元),但產出比原本的60×20=1 200(元)多了51.2元,因此是可行的。
五、轉化為統(tǒng)計問題的數學建模
統(tǒng)計知識在經濟、管理等多領域被廣泛應用,實際生活中出現的個數和成績等問題,常常需要轉化為統(tǒng)計問題,再利用有關知識加以解決。
例5 在日常生活中,我們經常會遇到用空瓶換汽水的問題。如果用m個空瓶可以換1 瓶新的汽水,當原有n瓶汽水時,最多能喝到多少瓶汽水呢?
教師引導學生列舉一些簡單、具體的實際情況來分析,如現有10 瓶汽水,用3 個空瓶可以換1 瓶新的,最多能喝到多少瓶汽水呢?師生共同探究得出答案:可以借來1個空汽水瓶,連同最后剩下的2個空汽水瓶一起再換1瓶新的,喝完后再還回去1個瓶子,所以最多能喝14+1=15(瓶)。教師引導學生從特殊到一般,共同解答此題。
解:每m個空瓶換1 瓶飲料,則當擁有(m-1) 個空瓶時,就可以借1個瓶子從而換得新的1瓶,然后把借來的瓶子歸還。因此,當喝完n瓶飲料得到n個空瓶后,又能得到瓶飲料,總共最多能喝(瓶),除不盡時則向下取整數。
【反思】題目中的量是抽象的m和n,沒有具體數量,看似很復雜,教師用特殊化方法,一步步地引導學生分析題意,找到解題方向,并解決特殊情況,然后從特殊情況出發(fā)探討一般情況,把看似困難的數學建模問題轉化為容易解決的統(tǒng)計問題。
在教學實踐中,教師要善于引導學生把生活中的問題轉化為方程、幾何、不等式、函數、統(tǒng)計類問題,并讓其經歷數學建模的過程,從而讓學生更好地學習數學建模,不斷提高數學建模能力。

