公路棄土場邊坡的穩定影響因素敏感性分析

丁文潔，馬祥配，彭永和，別鳳華，楊超，解露茜

(山東省第八地質礦產勘查院，山東地礦局有色金屬礦找礦與資源評價重點實驗室，日照地質地理信息大數據研究院，日照市土地質量評價與污染修復重點實驗室，山東 日照 276826)

0 引言

隨著我國經濟建設的加快，基礎設施建設不斷加強。在公路建設中由于受道路運輸等條件的限制，不可避免的會產生大量棄土棄渣，因而，在公路建設時必然要設置一定的棄土場來滿足棄土處置的需要[1]。

公路棄土場由于其欠固結、多孔隙、非飽和等結構特點[2]，在降雨及動力荷載的影響下極易發生失穩滑坡[3]。研究棄土場邊坡的穩定性，可以盡可能減小棄土場的潛在破壞性，對避免由于棄渣產生次生災害、減少水土流失具有重要意義。在棄土場的選址、支擋措施等設計中就可有針對性地采取相應的措施，達到安全、經濟和有效的目的。

目前，我國針對公路棄土場開展的研究很少。譚鵬[4]分析了棄土場失穩破壞機理并研究提出了棄土場穩定性分析方法，沈明祥[5]通過現場調查和計算分析評估了貴州省六盤水至威寧高速公路棄土場穩定性，鄭鶴丹[6]運用Geo Studio軟件對棄土體邊坡穩定性進行了評估，分析正常工況和非常工況條件下棄土體邊坡的穩定性，李研[7]對高速公路棄土場的處置方案進行了研究。以上文獻從分析機理、現場調查、計算分析、風險評價、處置方案設計等方面研究了高速公路棄土場的相關問題，但均缺乏穩定影響因素敏感性的分析。因此，在實際工作中，有必要結合具體工程實例對高速公路棄土場進行穩定影響因素敏感性分析，預防地質災害的發生。

公路棄土場在填筑過程中，需要根據棄土場的用途、穩定性，以及綜合經濟性等多種因素確定壓實控制標準。本文以日照市嵐山區某棄土場為例，通過MIDAS GTS NX進行數據模擬，在不同壓實控制標準的情況下，歸類分析高度和坡度對邊坡穩定性系數的變化規律，從而找到邊坡失穩的敏感因素。

1 敏感性分析原理

影響邊坡穩定的因素有坡角、坡高、黏聚力、內摩擦角、含水率、重度以及地震、降雨等，各因素對邊坡失穩的破壞程度是不同的，因此,通過邊坡穩定影響因素的敏感性分析，可以找出影響棄土場邊坡穩定的敏感因素，分析影響邊坡穩定性各因素與邊坡安全系數之間的相關性，即分析各因素的變化對于邊坡安全系數的影響程度[8]。

敏感性分析是系統分析中對系統穩定性的一種不確定性分析方法[9-10]。

本文通過MIDAS GTS NX進行模擬，計算出不同條件下的安全系數，然后選取任意一個影響因素在可能范圍內變化，且保持其他影響因素不變來計算安全系數，最后計算各影響因素的敏感性。

2 棄土場現狀

日照市嵐山區某棄土場，坡腳距實驗小學邊坡坡頂約10m。整個棄土場坡面平緩，坡面未見滑坡，坡頂未見裂縫、坍塌現象，整個坡面完整性好。

棄土場堆土巖性為素填土，最大厚度約6.0m，中密，濕，成分以回填風化巖碎屑為主；其下為殘積成因砂質黏性土，硬塑狀；底部為晉寧期花崗片麻巖，強風化，變晶結構，片麻狀構造，主要成分為石英、長石及其他暗色礦物，巖體呈致密的砂礫狀及角礫狀(圖1)。坡頂植被不發育。

1—填土；2—強風化花崗巖圖1 棄土場剖面圖

3 建立基本模型

3.1 建模

本文根據實際的邊坡坡面形態、各巖層巖性及其物理力學特征構建模型[12-14]。采用MIDAS-GTSNX軟件中的有限元強度折減法(SRM)[15-18]算出邊坡的等效應變塑性區及安全系數，以此分析邊坡穩定性。

模型分為兩個部分，分別是棄土場基底區A和棄土區B(圖2、圖3、圖4)，圖中單位為m，計算時線網格控制間距0.5m。

約束條件:模型左右兩側為水平約束,底部固定,上部及坡面為自由邊界。

本構模型:根據土體的應力應變特性,選取本構模型為Mohr-Coulomb模型。

初始應力:僅考慮自重應力產生的應力場。

計算收斂標準:收斂誤差小于定值10-6,最大迭代次數1000次，計算終止。重力加速度選取9.80665m/s2，幾何誤差0.0001。

圖2 一級邊坡二維模型(A)二級邊坡二維模型(B)

圖3 一級邊坡剖面等效應變云圖

圖4 二級邊坡剖面等效應變云圖

3.2 軟土強度參數試驗

堆放于棄土場的土主要為坡積粉質黏土，開展了直剪試驗[19]，得到了不同壓實度下的黏聚力、內摩擦角值和容重值(表1)。

表1 直剪試驗結果一覽表

4 模擬計算

根據前人[20]對工程邊坡進行過的研究，整理總結并通過現場工程地質勘查分析，影響邊坡穩定性的因素有很多[21]，主要影響因素有坡腳角度、邊坡高度、巖(土)體的抗剪強度性指標內摩擦角和巖(土)體的黏聚力[22]。壓實度決定了巖(土)體的抗剪強度性指標內摩擦角和巖(土)體的黏聚力，本文主要分析在不同壓實控制標準的情況下，研究坡腳角度、邊坡高度對邊坡穩定性系數的影響。

本文采用控制變量法[23]來探究邊坡穩定性，運用MIDAS GTS NX進行安全系數計算。假設該邊坡為均質土層，在不同壓實控制標準的情況下，選取不同的坡角β、坡高H，來獲得不同的安全系數，并對獲得的穩定系數進行分析。

(1)壓實度為90%時，黏聚力為28kPa，內摩擦角為14.6°，坡高分別選取5m、6m、7m、8m、9m、10m，坡比分別選取1∶0.5、1∶0.75、1∶1.00、1∶1.25、1∶1.50，得到相應的安全系數,詳見表2、表3。

表2 90%壓實度下不同坡高、坡比對應的安全系數(一級坡)

表3 90%壓實度下不同坡高、坡比對應的安全系數(二級坡)

(2)壓實度為92%時，黏聚力為33kPa，內摩擦角為15.3°，坡高分別選取5m、6m、7m、8m、9m、10m，坡比分別選取1∶0.5、1∶0.75、1∶1.00、1∶1.25、1∶1.50，得到相應的安全系數,詳見表4、表5。

表4 92%壓實度下不同坡高、坡比對應的安全系數(一級坡)

表5 92%壓實度下不同坡高、坡比對應的安全系數(二級坡)

(3)壓實度為95%時，黏聚力為41kPa，內摩擦角為15.5°，坡高分別選取5m、6m、7m、8m、9m、10m，坡比分別選取1∶0.5、1∶0.75、1∶1.00、1∶1.25、1∶1.50，得到相應的安全系數,詳見表6、表7。

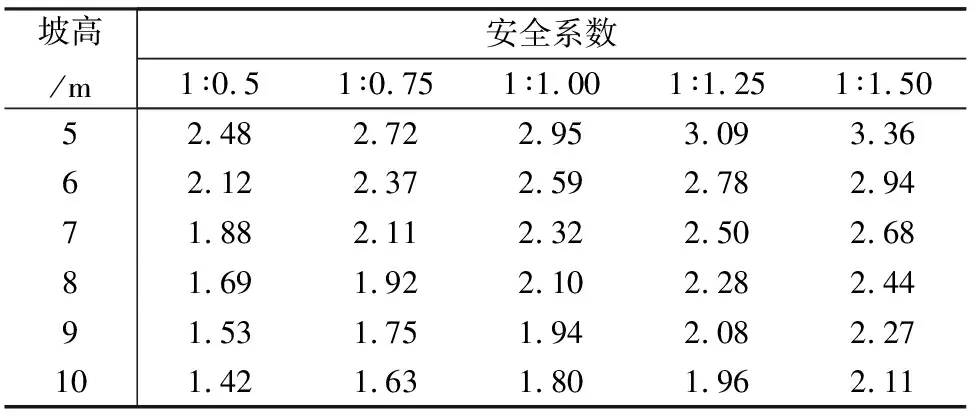
表6 95%壓實度下不同坡高、坡比對應的安全系數(一級坡)

表7 95%壓實度下不同坡高、坡比對應的安全系數(二級坡)

5 邊坡穩定性影響因素的敏感分析

公路棄土場在填筑過程中，已經根據實際需要確定了壓實控制標準。由于不同壓實控制標準決定了巖(土)體的內摩擦角和黏聚力，所以本次工作選取在不同壓實控制標準的情況下，改變坡高H、坡角β，進行影響因素的敏感分析。

5.1 邊坡高度的敏感性分析

利用數值模擬的結果(表2—表7),繪制坡高H與安全系數的關系圖(圖5)。通過圖5知,在相同的坡比下,坡高與安全系數呈向上凹的拋物線關系,且隨著坡高的增加,邊坡安全系數在不斷減小。坡高在5～7m范圍逐漸增大時，邊坡安全系數降低很快；在坡高在7～10m之間增大時，安全系數降低速率相較于穩定性系數在5～7m范圍內的變化要小。

a—90%壓實度一級坡坡高與安全系數關系圖;b—90%壓實度二級坡坡高與安全系數關系圖;c—92%壓實度一級坡坡高與安全系數關系圖;d—92%壓實度二級坡坡高與安全系數關系圖;e—95%壓實度一級坡坡高與安全系數關系圖;f—95%壓實度二級坡坡高與安全系數關系圖圖5 不同類別下坡高與安全系數關系圖

根據敏感度原理，計算出不同類別下棄土場坡高的敏感度，例如：90%壓實度一級坡，坡比為1∶0.5，當高度從7m減少到5m(降低約為28.57%)時，安全系數由1.42增加至1.89(增加約為33.10%)，棄土場坡高的敏感度約為1.158，而高度從7m增加到10m(增加約為42.86%)時，安全系數由1.42減小至1.08(降低約為23.94%)，棄土場坡高的的敏感度約為0.559。各個類別下的敏感度計算如表8。

(1)棄土場邊坡高度下降敏感度數值遠大于邊坡高度上升敏感度數值，由此可以得出：棄土場邊坡高度下降對安全系數影響比棄土場邊坡高度增加對安全系數影響敏感。

(2)隨著坡比的減小，無論邊坡高度下降還是增加，坡高對安全系數的影響有減小的趨勢,即說明隨著坡比的減小,邊坡高度的變化對穩定性的影響在減小。

(3)相同條件下，壓實度越大，無論坡高減小還是增加，坡高對安全系數的敏感度有下降的趨勢，說明壓實度越大，邊坡高度對安全系數的影響在減小。

表8 棄土場坡高敏感度統計表

5.2 邊坡坡比的敏感性分析

利用數值模擬的結果(表2—表7),繪制坡比與安全系數的關系圖(圖6)。通過圖6知,在相同的高度下,坡比與安全系數呈一定的線性關系,且隨著坡比由1∶0.5變化到1∶1.5,邊坡安全系數在不斷增大。

(1)棄土場坡比減小敏感度數值大于坡比增加敏感度數值，由此可以得出，棄土場坡比減小對安全系數影響比棄土場坡比增加對安全系數影響大。

(2)隨著高度的增加，無論坡比增加還是減小，坡比對安全系數的敏感度呈增加的趨勢，說明隨著高度的增加，坡比對安全系數的影響在增大。

根據敏感度原理，計算出不同類別下棄土場坡比的敏感度，例如：90%壓實度一級坡，坡高為5m，當坡比從1∶1.00增加到1∶0.50(增加約為100%)時，安全系數由2.40減少至1.89(減少約為21.25%)，棄土場坡高的敏感度約為0.213，而坡比從1∶1.00減小到1∶1.50(減小約為33.33%)時，安全系數由2.40增加至2.84(增加約為18.33%)，棄土場坡高的敏感度約為0.550。各個類別下的敏感度計算如表9。

(3)在相同高度下，壓實度越大，無論坡比增加還是減小，坡比對安全系數的敏感度減小，說明相同高度下，壓實度越大，坡比對安全系數的影響減小。

a—90%壓實度一級坡坡比與安全系數關系圖;b—90%壓實度二級坡坡比與安全系數關系圖;c—92%壓實度一級坡坡比與安全系數關系圖;d—92%壓實度二級坡坡比與安全系數關系圖;e—95%壓實度一級坡坡比與安全系數關系圖;f—95%壓實度二級坡坡比與安全系數關系圖圖6 不同類別下坡比與安全系數關系圖

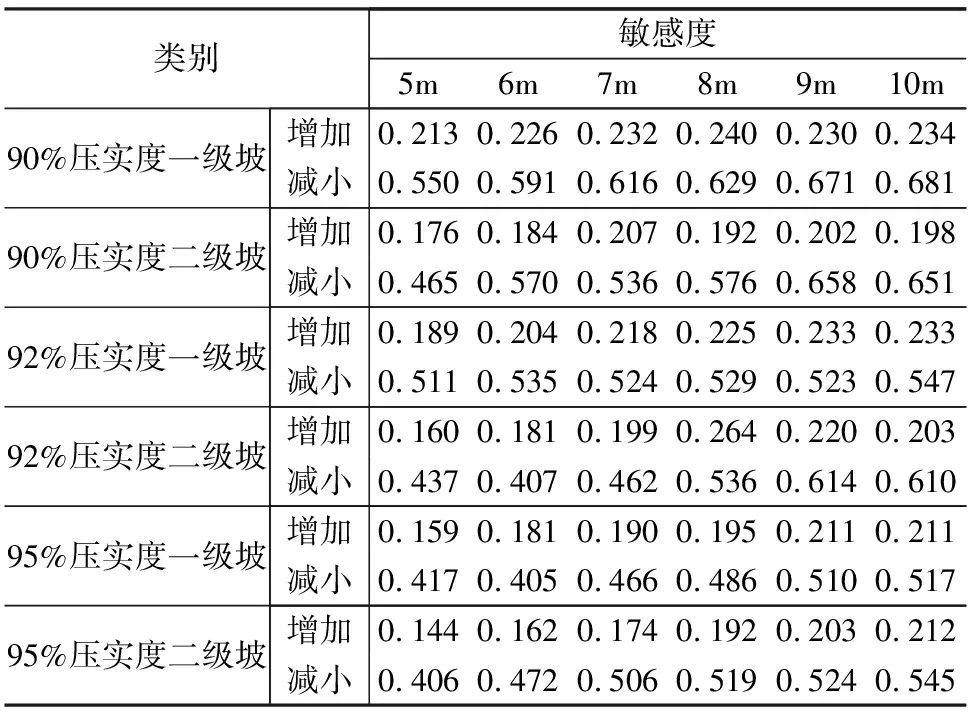
表9 棄土場坡比敏感度統計表

6 結論

利用MIDAS GTS NX軟件,對壓實度分別為90%、92%、95%，高度為5～10m,以及坡角為1∶1.50～1∶0.50的一級坡和二級坡進行了模擬,系統的對邊坡穩定性進行了分析。利用控制變量法,分析了在坡高和坡比單獨變化下邊坡的穩定性。利用敏感度,分析了在不同壓實控制標準下,坡高和坡比對安全系數的影響。以下為本文的主要結論:

(1)棄土場邊坡高度下降比棄土場邊坡高度增加對安全系數影響敏感；棄土場坡比減小比棄土場坡比增加對安全系數影響敏感。

(2)隨著坡比的減小,邊坡高度的變化對穩定性的影響在不斷減小；隨著高度的增加，坡比的變化對安全系數的影響增大。

(3)相同條件下，壓實度越大，邊坡高度和坡比對安全系數的影響越小。