低氣壓環境電氣化鐵路弓網電弧放電特性研究

景所立,魏 隆,陳 歡,李 杰,魯 超,母婷佑,陰國鋒

(1.中車青島四方機車車輛股份有限公司,青島 266000； 2.西南交通大學電氣工程學院,成都 611756)

引言

近年來，隨著高速鐵路技術的不斷進步，列車的運行速度也越來越高，伴隨而來的弓網電弧現象也越來嚴重[1]，電弧高溫、高能量的特性會對接觸線、受電弓滑板造成嚴重損傷[2]，已成為鐵路發展的重大阻礙之一。

對高原鐵路而言，弓網電弧帶來的危害將更為嚴重。某高原鐵路擬首次實現世界上速度等級最高的剛性接觸網懸掛結構，海拔高度高、氣壓低、氧氣稀薄[3-4]。上述特點將導致弓網耦合振動劇烈，電弧起弧閾值降低、強度增大，列車受流質量持續下降，嚴重影響列車安全穩定運行。故亟需針對高原鐵路特殊工況，開展高海拔、低氣壓環境下弓網電弧放電特性的相關研究，為高原鐵路的建設奠定理論基礎。

為進一步了解弓網電弧特性，保障鐵路牽引供電系統及列車的運行安全，國內外學者針對弓網電弧模型、弓網電弧電氣特性、弓網電弧電磁干擾等方面展開了大量實驗與仿真研究。在弓網電弧模型的研究方面，韓偉鋒等[5]利用流體動力學方程和麥克斯韋電磁場方程建立了弓網電弧的MHD數學模型、二維流固耦合模型，研究了弓網電弧的形態、電流密度和電場的分布特性。朱光亞等[6]根據弓網電弧周圍電磁場、熱場和氣流場的耦合關系，搭建了弓網多物理場耦合模型，并對弓網電弧的發生發展特性進行了研究。在弓網電弧電氣特性的研究方面，徐旻等[7]針對弓網電弧伏安特性進行了分析，發現燃弧尖峰電壓隨弓網間隙距離的增加呈指數增長關系。喬凱等[8]基于改進的Mayr模型，發現列車運行速度越高，電弧耗散功率越高， 燃弧尖峰電壓和熄弧尖峰電壓也越高。在弓網電弧電磁干擾的研究方面，陳嵩等[9]運用Simulink軟件搭建了弓網電火花噪聲仿真模型，并進行了弓網電弧對鐵路通信系統的干擾現象的分析與預測。黃金磊等[10]基于FEKO軟件對弓網離線電弧的電磁場的分布和衰減特性進行了研究，發現弓網電弧頻率越高，其衰減速度也越快。

某高原鐵路沿線海拔高、氣壓低，勢必會對弓網電弧特性造成影響，但國內外與其相關的研究卻寥寥無幾，更多的是關于氣壓對開關電弧和絕緣子的污閃特性影響的研究[11-15]，針對低氣壓環境弓網異質異構電極的放電特性的研究相對較少，因此依托某高原鐵路工程建設，亟需開展低氣壓環境弓網電弧放電特性分析研究。本文運用Comsol電流、磁場、傳熱以及層流四大模塊，基于電弧MHD模型，建立了低氣壓環境弓網電弧模型，對不同氣壓下弓網電弧的電壓特性、溫度場特性、電流密度特性進行了研究，并通過實驗獲得了不同氣壓下的電弧圖像、拉斷距離等實驗結果，驗證了仿真結果的正確性。

1 模型描述

1.1 簡化幾何模型

由于弓網電弧受電場、磁場、溫度場、氣流場等多個物理場耦合的影響，其本身的規律又有一定隨機性，對弓網電弧直接進行仿真較為困難，因此需要對仿真模型進行簡化，以提升仿真模型的收斂性。

仿真采用的簡化弓網系統二維模型如圖1(a)所示，接觸線直徑設為13 mm。為使接觸線更穩固地架設在接觸網上，需要用接觸線固定線夾固定在溝槽上，因此在幾何模型中也設計了兩個接觸線溝槽，其角度為89.4°，兩溝槽間距為5.22 mm[16]。受電弓滑板尺寸為5 mm×30 mm，弓網間距設為4 mm。

當用此模型進行計算后，發現網格需剖分得很細才能得到收斂的運算結果，尤其是溝槽區域的網格需要進行超細化甚至極細化處理，這極大地減慢了運算速度，因此需對弓網電弧幾何模型進一步簡化。進一步分析發現，對弓網電弧形態、溫度等特征起決定性作用的是接觸線底部區域以及受電弓滑板頂部區域，而溝槽區域只是對接觸線起固定作用，對弓網電弧影響不大。因此，可去掉接觸線溝槽部分，只保留其底部，得到簡化后的幾何模型如圖1(b)所示。

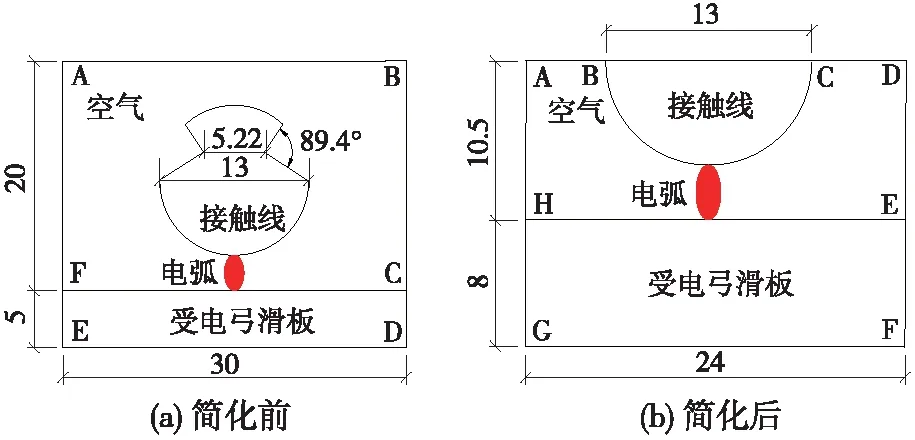
圖1 弓網電弧幾何模型(單位：mm)

1.2 材料物性參數設定

在弓網電弧模型中，材料物性參數包括電極材料(受電弓滑板、接觸網導線)以及弓網間隙空氣參數。接觸網導線選取直徑為4 mm的紅銅材料，其優點是導電性能優異、耐燒蝕性能好，適合進行電弧放電特性研究；受電弓滑板選取純碳滑板，其優點是在弓網滑動磨損時主要磨損滑板，從而保護接觸線材料，降低接觸線材料的更換頻率。電極材料具體的參數如表1所示。

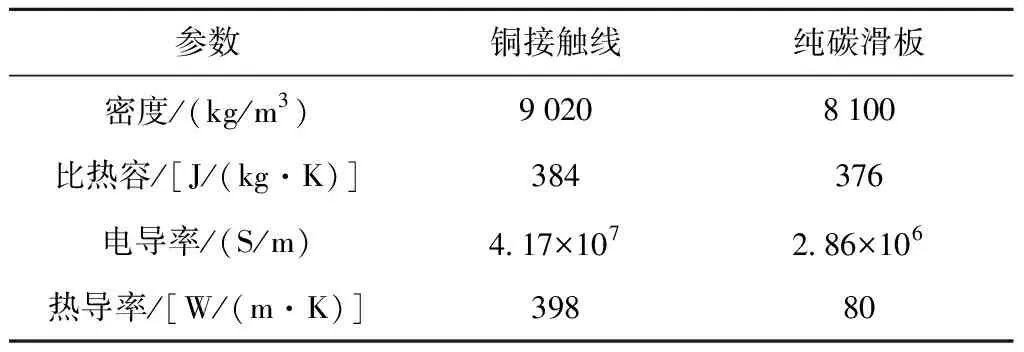
表1 電極材料參數

對于空氣參數的設定，其情況較為復雜。對于相對介電常數和相對磁導率，默認為1，但對于電導率和比熱容等參數，并不能簡單地用一個常數來表示。由于電弧本身的溫度很高，與環境設定的初始溫度相比差異極大，并且兩電極之間的電流流通是以電弧作為導體的，因此可以判斷空氣在電弧各區域由于溫度的不同其參數也會發生改變。且在不同的氣壓等級下，空氣的密度、比熱容、電導率、熱導率等參數也會發生變化。

為了使仿真結果更加精確，空氣區域的參數需要與實際情況盡可能一致。因此，在仿真模型中設置了隨環境溫度和氣壓變化的空氣參數，10.1 kPa(0.1 atm)，30.3 kPa(0.3 atm)，50.5 kPa(0.5 atm)，101.0 kPa(10.1 atm)四個氣壓等級下的空氣密度、比熱容、電導率、熱導率隨溫度變化曲線rho(T)、Cp(T)、sigma(T)、k(T)分別如圖2(a)、圖2(b)、圖2(c)、圖2(d)所示[17]。

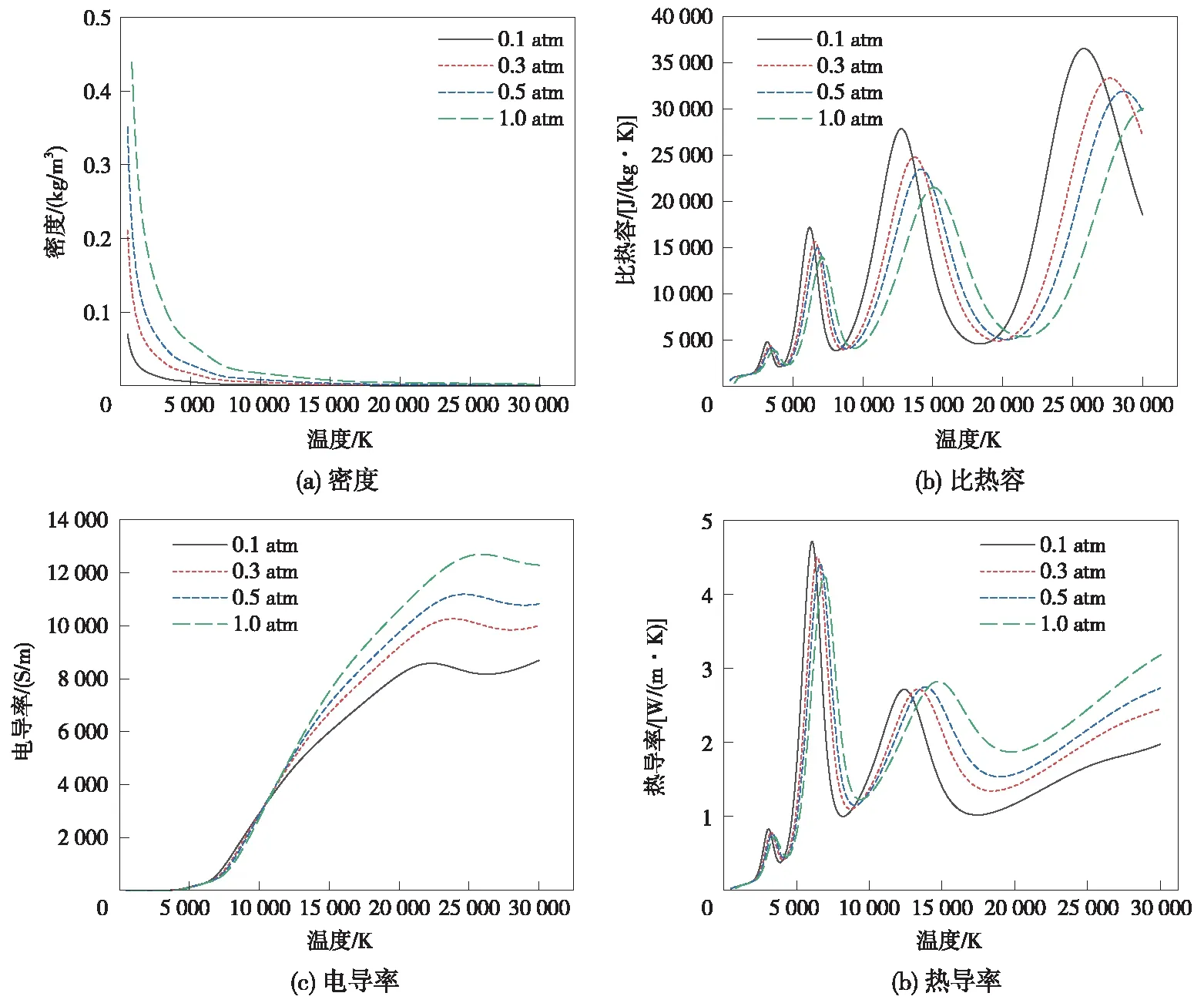
圖2 不同氣壓等級下空氣參數隨溫度變化曲線

1.3 電弧數學模型

弓網電弧模型是基于磁流體動力學理論建立的，該理論包括流體動力學方程、電磁場方程[18]。流體動力學方程是描述流體運動的基本方程組，主要包括流體質量守恒方程、動量守恒方程及能量守恒方程，電磁場方程主要包括Maxwell方程組，是研究電弧特性必不可少的工具。具體方程如下。

(1)質量守恒方程

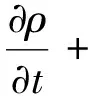
(1)

式中，ρ為電弧密度，kg/m3；t為時間，s；v為電弧等離子體的流場速度，m/s。

(2)動量守恒方程

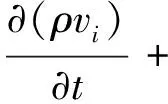
(2)

式中：vi為i=(r，z)方向上的速度分量，m/s；η為動力黏度，Pa·s；p為壓強，Pa；J為電流密度，A/m2；B為磁感應強度，T。

(3)能量守恒方程

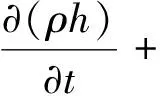
(3)

式中，h為焓；λ為熱導率；cp為比定壓熱容；Sh為能量源項，是電弧等離子體的能量來源，可通過式(4)計算得到

(4)

式中，σ為電弧等離子體電導率，S/m；V為流體粘性耗散項；J2/σ為電流流過電弧等離子體所產生的焦耳熱；QR為電弧等離子體通過輻射向外散發的能量。

(4)Maxwell方程

電弧電場φ的計算方程為

?·(σ?φ)=0

(5)

電弧電流密度矢量為

J=-σ?φ

(6)

電弧電流自感生電場的B0為

?×H0=J

(7)

B0=μ0(H0+M)

(8)

M=B0(μr-1)/μ0

(9)

或者

(10)

根據畢奧-薩伐爾定律，計算得接觸線電流產生的磁場為

(11)

綜上，電弧等離子體總的磁感應強度為

(12)

1.4 邊界條件

首先針對溫度場邊界條件進行設置，將空氣區域的溫度設置為293.15 K，接觸線頂部與受電弓滑板底部的溫度初始值設置為293.15 K，其余邊界上的溫度設為自然對流換熱，其溫度滿足如下方程

q·n=h(T-T0)

(13)

然后，對層流場邊界條件進行設置，空氣區域設置為一個標準大氣壓(1atm)，將受電弓滑板和接觸線設置為內壁(無滑移)邊界條件，模擬一個標準大氣壓下的仿真環境。并將邊界AB、CD、DE、HA設為開邊界，其他邊界不進行設置。

對于電流邊界，將受電弓滑板的底部邊界設置為接地邊界條件，電勢為0V；將接觸線底部設置為邊界電流源；將滑板頂部和接觸線的電極鞘層區域設置為電流守恒邊界條件[16]，并設置所有邊界為電絕緣邊界條件。

對于磁場部分，根據電磁場方程設置各區域所需磁場大小，并設置所有邊界為磁絕緣邊界條件，如表2所示。

表2 仿真邊界條件

2 仿真結果與分析

2.1 高海拔環境弓網電弧電壓特性分析

為探究高海拔環境弓網電弧放電特性，針對高海拔環境弓網電弧的電壓進行了研究。將電流設為50 A，弓網間距設為4 mm，空氣壓強分別設為101.0，50.5，30.3，10.1 kPa，在COMSOL中繪制出不同氣壓下弓網系統電勢分布圖，如圖3所示。

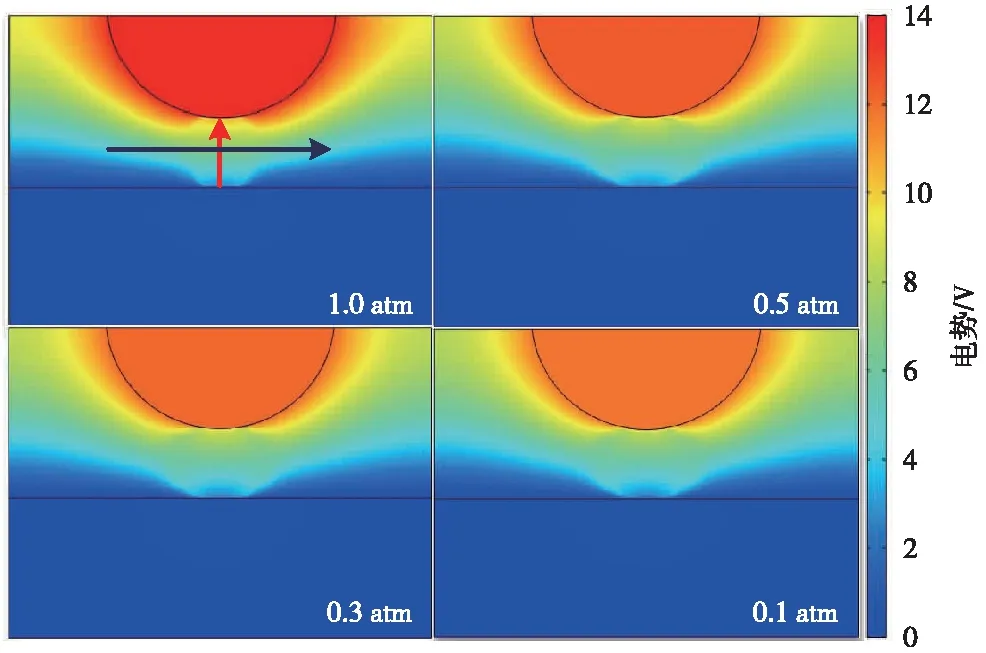
圖3 不同氣壓等級下弓網系統電勢分布

為更直觀地了解弓網系統電勢的具體分布，截取弓網系統軸向電勢數據進行分析，如圖3(a)中紅線所示，截取線原點(軸向距離為0處)為滑板頂部。繪制出不同氣壓下弓網電弧軸向電勢曲線，如圖4所示。

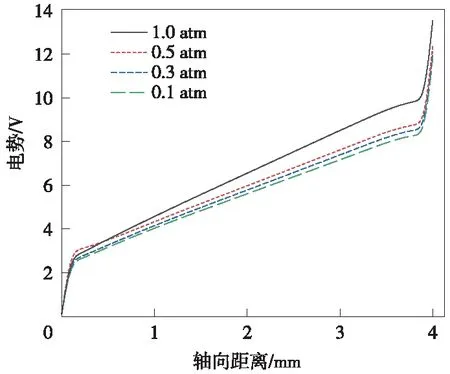
圖4 弓網電弧軸向電勢分布

從圖4可看出，弓網電弧軸向各點電勢隨氣壓的降低而降低，在電弧兩極區域存在明顯的電勢突變現象。且101.0,50.5,30.3,10.1 kPa下弓網電弧電壓分別為13.54,12.39,12.12 V和11.84 V，因此，氣壓越低，弓網電弧軸向電壓也越低。這主要是因為氣壓越高，空氣熱導率越高，使得電弧加速散熱，促進了電弧的去游離過程，需要通過電源補償更高的電壓來維持電弧燃燒，從而使電弧電壓升高[19]。且從圖4可看出，靠近電極區域單位距離壓降明顯大于弧柱區域。

2.2 高海拔環境弓網電弧溫度特性分析

為了分析不同氣壓對弓網電弧溫度的影響，分別將氣壓設為101.0,50.5,30.3 kPa和10.1 kPa，對這四種氣壓下的弓網系統溫度場分布情況進行仿真。為了更直觀地分析氣壓對弓網電弧溫度值的影響，分別按圖3(a)所示的紅色與黑色截線截取了弓網電弧軸向、徑向溫度數據，繪制了不同氣壓下的弓網電弧軸、徑向溫度分布，分別如圖5和圖6所示。在圖5(a)中，以軸向距離y=0.5 mm和y=3.5 mm為界將電弧劃分為陰極區、弧柱區和陽極區三部分，三者在不同氣壓下弓網電弧軸向溫度分布分別如圖5(b)、圖5(c)、圖5(d)所示。在圖6(a)中以徑向距離x=-1 mm和x=1 mm為界將電弧劃分為弧柱中心區和弧柱邊緣區，不同氣壓下弓網電弧弧柱中心區徑向溫度分布如圖6(b)所示。

圖5 不同氣壓下弓網電弧軸向溫度分布

如圖5(a)所示，弓網電弧軸向溫度近似呈馬鞍型，且陽極區域的軸向溫度均顯著高于陰極區域。這是由于弓網電弧兩電極材料不一樣導致的，陽極區域為銅材料，熱導率比陰極區域的碳材料要高，導熱能力較強，因此陽極區域電弧溫度較高[6,16,20]。

由圖5(a)可進一步得到：在101.0,50.5,30.3,10.1 kPa氣壓下，弓網電弧陰極區最高溫度分別為12 206,11 945,11 083,10 929 ℃，弧柱區最高溫度分別為9 771,9 706,9 661,9 610 ℃，陽極區最高溫度分別為16 500,16 071，15 715,15 113 ℃。即隨著氣壓的降低，弓網電弧軸向溫度逐漸降低，且在電弧兩極區域這一現象最為明顯。一方面，電弧溫度與電弧能量關系密切，氣壓的降低會使空氣分子自由程變長，粒子間的碰撞幾率減小，導致電弧溫度降低[19]。另一方面，氣壓降低時空氣比熱容會隨之下降[17]，導致弓網電弧吸收在吸收相同熱量的情況下溫度的上升幅度較小，在以上兩方面因素的綜合影響下，弓網電弧溫度隨氣壓降低而降低。

由圖6所示，隨著氣壓的降低，弓網電弧弧柱中心區溫度隨氣壓降低而降低的趨勢較為明顯，且最高溫度分別為9 298,9 257,9 245,9 207 ℃，而弧柱邊緣區溫度幾乎不變。

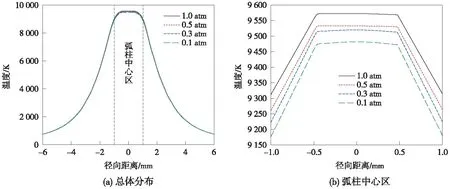
圖6 不同氣壓下弓網電弧徑向溫度分布

2.3 高海拔環境弓網電弧電流密度特性分析

為了分析不同氣壓對弓網電弧電流密度的影響，分別將空氣氣壓設為101.0,50.5,30.3和10.1 kPa，對這4種氣壓下的弓網系統電流密度分布情況進行仿真。

為了更直觀地分析氣壓對弓網電弧電流密度值的影響，截取弓網電弧軸、徑向電流密度數據，繪制了弓網電弧軸、徑向電流密度分布，如圖7和圖8所示。

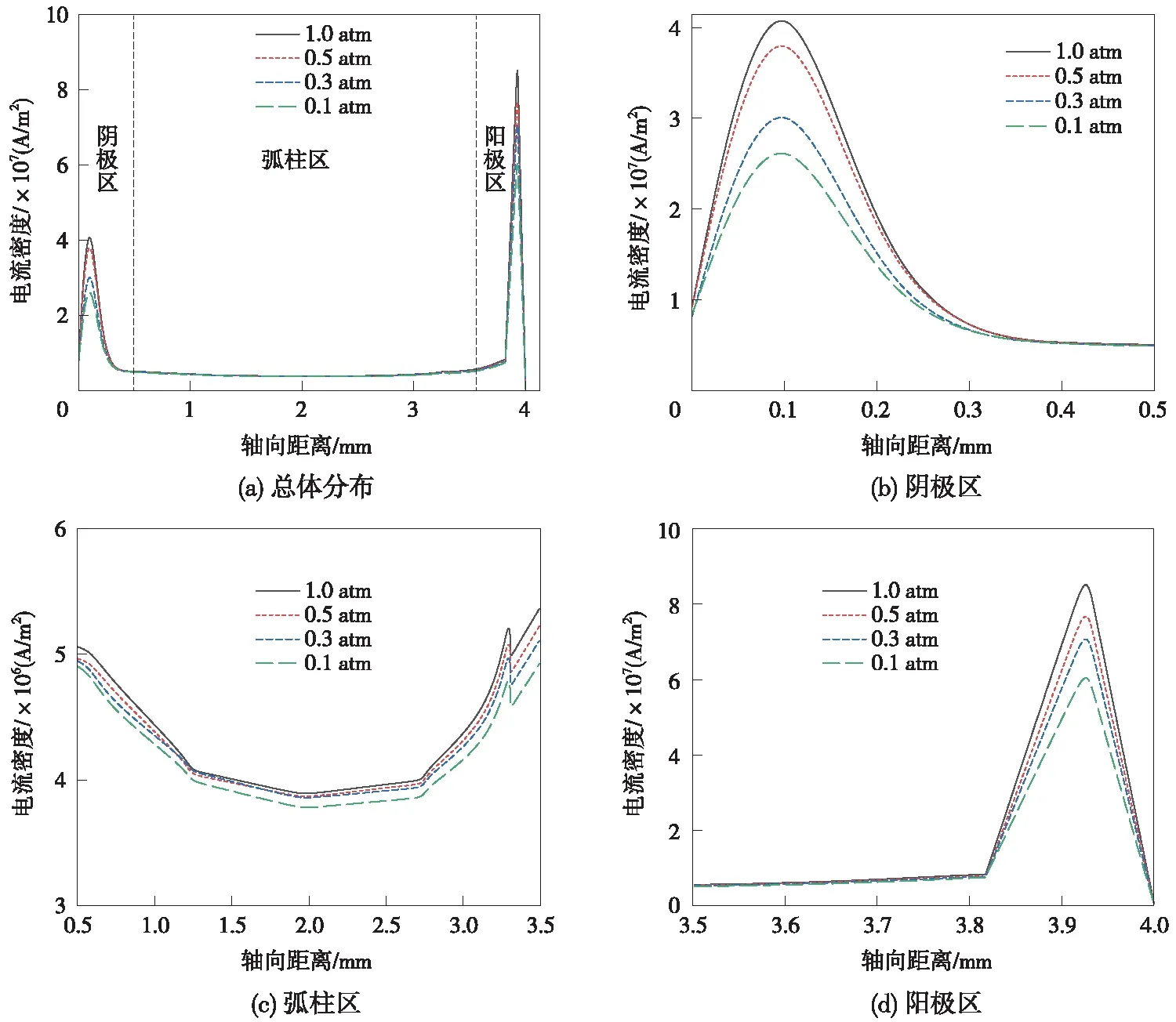
圖7 不同氣壓下弓網電弧軸向電流密度分布

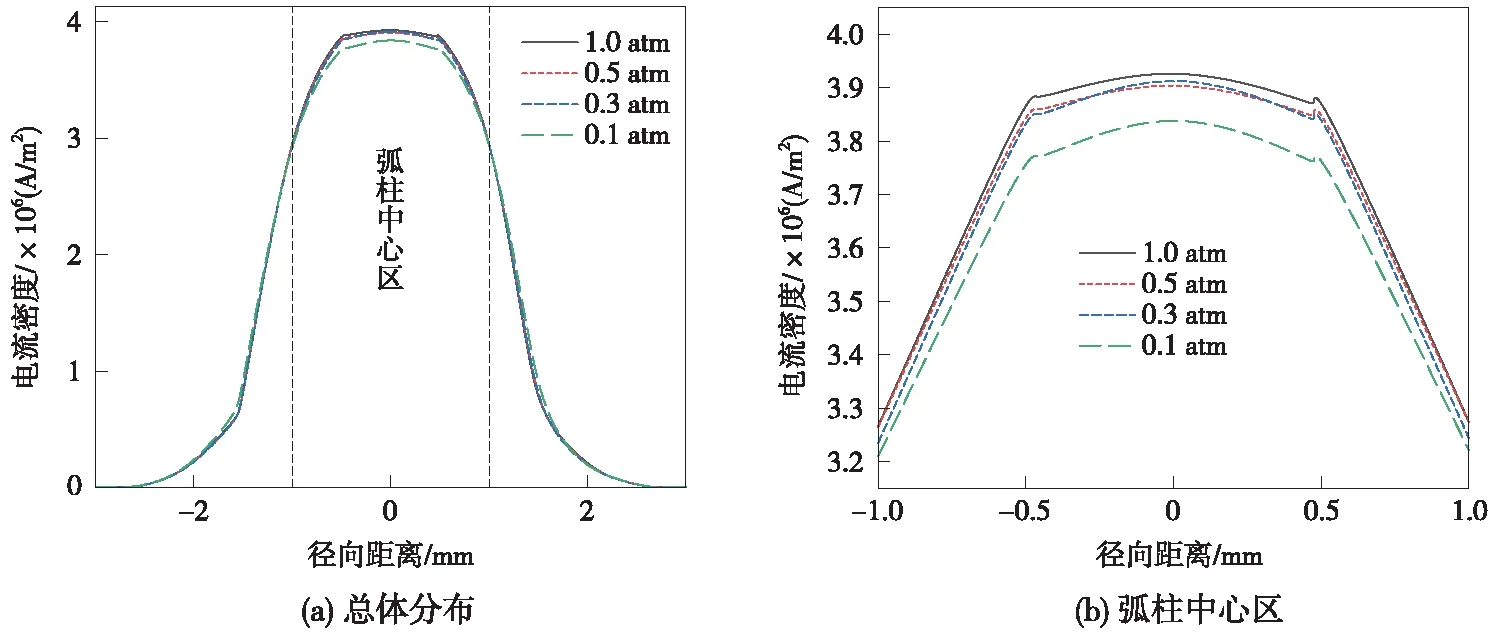
圖8 不同氣壓下弓網電弧徑向分布

由圖7可得到：在101.0,50.5,30.3,10.1 kPa氣壓下，弓網電弧陽陰極區最高電流密度分別為4.08×107，3.81×107，3.01×107，2.62×107A/m2，弧柱區最高電流密度分別為5.37×106，5.23×106，5.12×106，4.92×106A/m2，陽極區最高溫度分別為8.53×107，7.69×107，7.08×107，6.05×107A/m2。即隨著氣壓的降低，弓網電弧軸向電流密度逐漸降低，且在電弧兩極區域這一現象最為明顯。這是因為：一方面，氣壓的降低會增大空氣分子自由程，粒子間的碰撞次數減少，導致粒子間碰撞電離率減小[19]；另一方面，空氣電導率隨氣壓降低而減小[17]，導致傳導電子的能力減弱，使電弧電流密度減小。以上兩方面原因綜合導致了弓網電弧電流密度隨氣壓降低而減小。

3 實驗驗證

為了驗證上述仿真結果，搭建了弓網電弧放電實驗平臺，該平臺主要由限流電阻(5 Ω)、兩電極材料、直流電源、精密升降臺、高速相機以及示波器組成，如圖9(a)所示。同時為實現低氣壓的環境，實驗中使用氣壓調節范圍為5～100 kPa的環境氣壓艙來調節氣壓的高低。

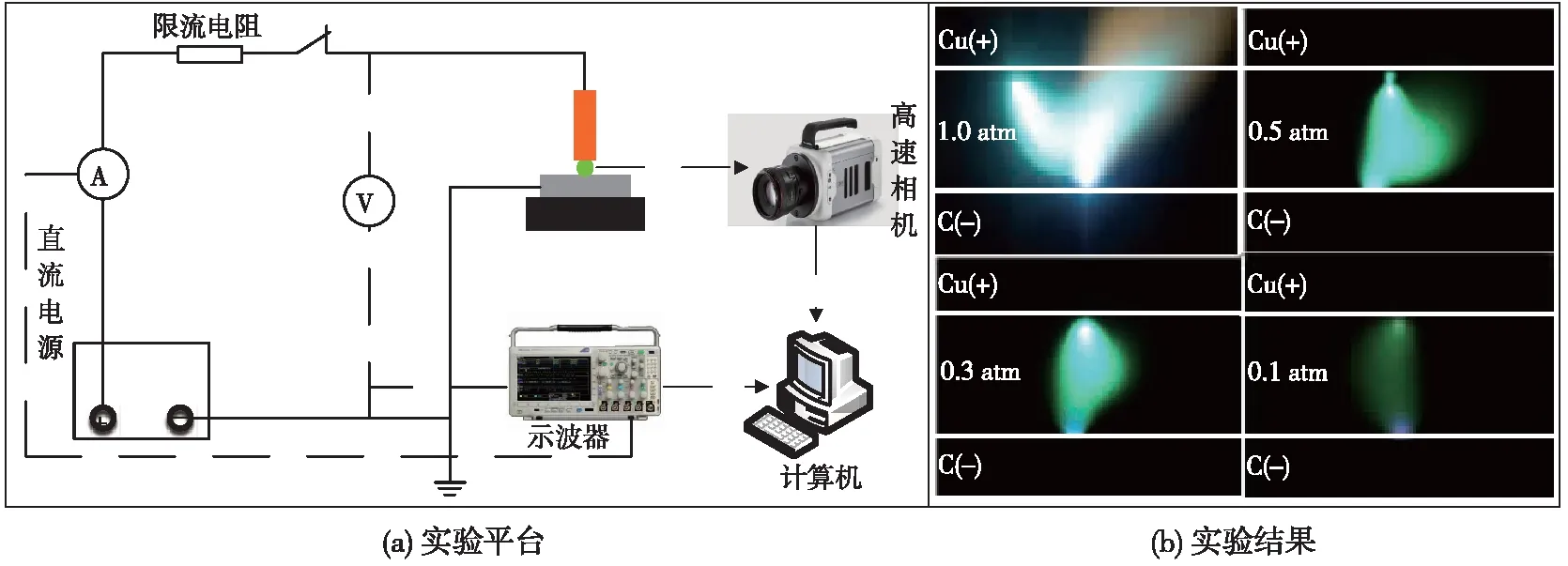
圖9 不同氣壓下弓網電弧形態對比

將銅接觸線作為陽極，純碳滑板作為陰極，并用砂紙打磨平整后分別固定在實驗平臺框架和精密升降臺上，利用直流恒流電源將電源電壓設定為200 V，電流設定為50 A，拉弧時間設定為10 s，最大拉弧距離設定為10 mm。精密升降臺由伺服電機配合渦輪絲桿減速機完成升降操作，其中伺服電機通過給定脈沖數及單位時間脈沖數來控制升降臺的位移距離及位移速度。

改變實驗氣壓條件，分別設為101.0,50.5,30.3,10.1 kPa待確認兩電極材料充分接觸后(接觸電阻約為10 mΩ)，進行低氣壓環境弓網電弧放電實驗，并使用高速相機記錄電弧燃弧過程，得到4種氣壓下的弓網電弧形態，如圖9(b)所示。

從圖9(b)可以發現，氣壓的高低會影響弓網電弧的燃弧過程。在同一弓網間距下，隨著氣壓的增大，弓網電弧燃燒程度越劇烈、產生的弧光越明亮。實驗拍攝的電弧圖像亮度隨氣壓的降低而減弱，這也意味著在同一弓網間距下，弓網電弧溫度隨氣壓降低而降低，與仿真結果吻合。從圖9(b)中還可以發現，在鄰近電極區域觀察到亮斑，陽極區亮度高于陰極區，表明弓網電弧兩極區域溫度高于弧柱區域，且陽極區溫度最高，與上述仿真結果一致。

弓網電弧維持能力是電弧燃弧過程的重要表征量，可用弓網電弧拉斷距離表示，弓網電弧拉斷距離即弓網電弧被拉斷一瞬間的弓網間距。一般而言，弓網電弧的拉斷距離越長，則表示電弧燃弧時間越長、熄弧越困難，由弓網電弧造成的危害越嚴重。為進一步探明低氣壓環境對弓網電弧維持能力的影響，將電流設為50 A，電極拉斷速度設為40 mm/s，在電壓分別為200，300，400，500 V的條件下測得不同氣壓等級下電弧的拉斷距離，如圖10所示。

由圖10可知，氣壓與弓網電弧的拉斷距離呈指數型關系。隨著氣壓的降低，弓網電弧的拉斷距離呈非線性增長，從101.1 kPa的135 mm增大至20.2 kPa的279 mm。即氣壓越低，弓網電弧拉斷距離越長，代表電弧維持能力越強，熄弧越困難，對滑板的侵蝕作用越強。這是因為根據氣體介質電場強度理論，在一定范圍內弧柱電場強度與氣壓成正比，即弧柱電場強度隨氣壓的降低而減小[21]。因此，低氣壓下需要更大的弓網間隙才能保證電源電壓低于電弧電壓，即滿足熄弧條件。依據上述理論，低氣壓下維持電弧所需電壓降低，即在同一間隙下，電弧電壓隨氣壓降低而降低，與仿真結論一致。

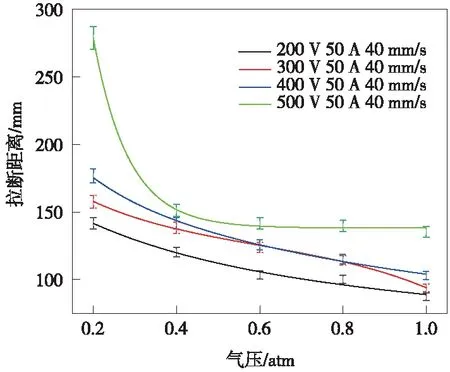
圖10 不同氣壓下弓網電弧拉斷距離

4 結論

基于準確的空氣電弧物性參數，在多物理場仿真軟件COMSOL Multiphysics中建立了考慮氣壓影響的弓網電弧仿真模型。利用該仿真模型針對氣壓對弓網電弧電壓、溫度、電流密度的影響進行仿真研究。進一步通過電弧實驗平臺獲得不同氣壓下的電弧圖像、拉斷距離等實驗結果，補充和豐富了氣壓影響弓網電弧的認識，同時驗證了仿真結論的正確性。主要結論如下。

(1)弓網電弧電壓隨氣壓的降低而降低。隨著弓網間隙氣壓從101.0 kPa降為010.1 kPa，弓網電弧軸向各點電勢不斷下降，電弧電壓從13.54 V降為11.84 V；靠近電極區域單位距離壓降明顯大于弧柱區域。

(2)弓網電弧溫度隨氣壓的降低而降低。隨著弓網間隙氣壓從101.0 kPa降為10.1 kPa，電弧軸向最高溫度從16 500 ℃下降至15 113 ℃；且弓網電弧與電極相鄰區域溫度顯著高于弧柱區溫度。實驗拍攝的電弧圖像亮度隨氣壓的降低而降低，且在臨近電極區域觀察到亮斑，與仿真結果一致。

(3)弓網電弧維持能力隨氣壓的降低而增強。在500 V電壓下進行拉弧實驗，弓網電弧的拉斷距離從101.0 kPa的135 mm增大至20.2 kPa的279 mm。表明低氣壓下維持電弧所需電壓降低，弓網電弧維持能力增強，將造成更嚴重的危害，在高原地區鐵路的建設和運營中應更加予以注意。