基于雙尺度理論優化混凝土力學性能的研究

高皓宸　李偉　張旭東

摘要：為了實現混凝土抗壓強度及彈性模量的精細化數值計算，基于雙尺度理論建立了混凝土雙尺度數值模型。該理論以有限元方法為載體，通過正交試驗對混凝土抗壓強度和彈性模量的影響因素進行了分析，并進行了力學試驗驗證。研究結果表明：1）雙尺度理論在混凝土數值模擬中的應用具有可行性，運用該方法的數值結果與試驗結果差值在4.22%之內;2）混凝土的抗壓強度受細觀參數影響高度顯著，其中砂漿性能對整體抗壓強度的影響比例可達24.35%;3）混凝土的彈性模量受細觀參數影響顯著，其中粗骨料性能對整體彈性模量的影響比例可達6.55%。研究結果揭示了混凝土內部的粗骨料、砂漿、界面過渡區與孔隙對整體性能的影響效應，為優化和設計新型混凝土材料提供了新思路。

關鍵詞：非金屬建筑材料;雙尺度理論;有限元方法;混凝土數值模擬;正交試驗

中圖分類號：TU5281文獻標識碼：A

DOI： 10.7535/hbgykj.2022yx02009

Study on optimizing mechanical properties of concrete based on two-scale approach

GAO Haochen LI Wei ZHANG Xudong

（1School of Urban Planning and Municipal Engineering，Xi′an Polytechnic University，Xi′an，Shaanxi 710600，China;2Network Information Center，Xi′an Jiaotong University，Xi′an，Shaanxi? 710049，China）

Abstract：In order to realize the refined calculation of concrete compressive strength and elastic modulus，a two-scale numerical model of concrete was established based on the two-scale approachThe finite element method was taken as the carrier of this approach，the influencing factors of concrete compressive strength and elastic modulus were analyzed through orthogonal experiment，and the result was verified by mechanical testThe results show that：1） the application of two-scale approach in numerical simulation of concrete materials is feasible，and the difference between the numerical results and the experimental results is within 4.22%;2） the compressive strength of concrete is significantly affected by meso parameters，and the influence proportion of mortar on the overall compressive strength is up to 24.35%;3） the elastic modulus of concrete is significantly affected by meso parameters，and the influence proportion of coarse aggregate on the overall elastic modulus is up to 6.55%The effects of coarse aggregate，mortar，interface transition zone and pores in concrete on the overall performance is revealed through the research results，which provide new methods for the optimization and design of new concrete materials

Keywords： non-metallic building material;two-scale approach;finite element method;numerical simulation of concrete;orthogonal experiment

混凝土是土木工程中最常用的材料之一。在宏觀尺度下，混凝土被假定為一種各向同性的均質材料;在細觀尺度下，混凝土表現為由粗骨料、硬化的水泥砂漿、兩者之間的界面過渡區（interfacial transition zone，ITZ）以及孔隙等構成的多相復合材料。

WITTMANN等[1]首次提出了“混凝土的細觀結構”，將基于細觀結構的研究思路和方法引入到混凝土材料宏觀性能的研究中，該研究為探索混凝土力學性能提供了一種精細化方法。劉光廷等[2]提出的隨機骨料模型已成為混凝土細觀結構建模使用較為廣泛的方法之一。馬懷發等[3]采用隨機骨料法對鋼筋混凝土梁進行了抗彎實驗分析。趙吉坤[4]采用對砂漿性能弱化的方法來模擬孔隙和微裂紋對混凝土宏觀力學性能及細觀破壞的影響。宋來忠等[5]將復合材料的增強顆粒形狀構建為星形，提供了創建更加接近真實試件的幾何模型方法。田夢云等[6]研究了各種因素對混凝土宏觀應力-應變關系和最終破壞模式的影響。

上述研究中，針對混凝土細觀結構中的界面過渡區以及孔隙實體對混凝土整體性能和破壞模式的影響研究還不夠深入，且研究的數值模擬邊界條件也存在著與實際混凝土力學試驗不符的問題。基于此，本研究將雙尺度理論作為理論基礎，根據自編程序模擬四相混凝土的幾何結構，通過模擬不同工況下的數值實現混凝土宏觀等效力學參數的計算。

1混凝土數值模擬方法

1.1細觀-宏觀雙尺度理論

混凝土是一種典型的多相復合材料，根據LI等[7]的復合材料雙尺度理論，對具有兩相或多相復合材料建立坐標系，如圖1所示[7]。

基于復合材料力學量的漸進展開式和攝動理論，將雙尺度位移場分解為宏觀和細觀2個尺度。

1.2混凝土數值模型

1.2.1混凝土雙尺度模型

本研究的數值模擬方法以雙尺度理論為基礎，而雙尺度公式的形式為有限元微分方程組，因此有限元法相對于離散元法等更適合作為數值模擬的載體。筆者將包括粗骨料、水泥砂漿、界面過渡區與孔隙在內的四相模型用于混凝土抗壓強度及彈性模量的有限元數值模擬。混凝土粗骨料按形狀可分為碎石與卵石。王曉琴等[8]提出不規則粗骨料顆粒比圓形粗骨料顆粒更能反映真實骨料的特點，計算結果也更接近于宏觀試驗。故模型中的碎石骨料被模擬為隨機多邊形，單個粗骨料示例如圖2 a）所示。其中，所有粗骨料在整體模型中的分布采用了隨機均勻算法。同時，粗骨料的級配滿足二維模型常用的Walraven表達式，如式（11）所示，且基于文獻[9]的算法保證骨料之間不會發生相交情況。

混凝土內部常常含有孔隙或微裂縫，它們對混凝土力學性能和失效破壞模式會產生影響。陳青青等[10]提出圓形、橢圓形、多邊形孔隙對計算精度影響有限，而圓形孔隙的計算效率明顯高于其他兩種。因此模型中的孔隙被模擬為圓形，孔隙在混凝土模型中滿足隨機均勻分布。

水泥砂漿在混凝土中起著膠結作用。混凝土的破壞往往發生于砂漿內部以及砂漿與骨料的交界處，砂漿強度性能對混凝土力學特性影響高度顯著[11]。

RAO等[12]認為在砂漿與骨料的交界處存在ITZ，這是由于壁效應以及骨料顆粒周圍水泥水化產生的孔隙而形成的。ITZ的材質與砂漿差別不大，但是其內部疏松多孔，因此ITZ容易成為混凝土整體的薄弱部位。ITZ幾何由已建成的粗骨料模型進行縮放而成，其厚度為100 μm，如圖2 b）所示。

1.2.2邊界條件與網格劃分

雙尺度模型處于單軸受壓狀態時的邊界條件應設置為底邊中點的橫向與縱向位移約束、底邊其余點的縱向位移約束以及頂邊的縱向位移荷載[13]，如圖3所示。

網格劃分及細部結構如圖3所示，網格單元為四邊形為主的線性平面應變單元。其中，對于橫截面尺寸沿縱軸不變、受有平行于橫截面而且不沿縱軸變化的面力或約束的物體，平面應變模型可以將其簡化為二維模型進行分析，相較于三維模型提高了計算效率。

1.3材料參數

基于文獻[14]—[16]中的相關規范參數賦予混凝土各組成相力學參數。一般情況下，粗骨料的抗壓強度遠高于水泥砂漿和界面過渡區，數值模擬時，粗骨料被假定為線彈性材料[17]，粗骨料的參數如表1所示。水泥砂漿屬于脆性材料，其抗拉強度遠小于其抗壓強度，因此砂漿的塑性損傷本構關系應分為抗壓與抗拉參數[5-6]，水泥砂漿的強度等級如表2所示。界面過渡區只存在于骨料與砂漿表面的交界處，其力學性能一般為砂漿的60%～80%[18-19]。界面過渡區的力學性能可以等價為水泥砂漿力學參數按一定比例的“弱化”，筆者將水泥砂漿與界面過渡區之間的弱化系數設置為08，如表3所示。

1.4數值模擬方法總流程

基于雙尺度理論和有限元方法的混凝土雙尺度模型數值模擬總流程圖如圖4所示，總體可分為以下4步。

步驟1：輸入模型的細觀組成相參數，進而生成各組成相的幾何模型。

步驟2：將生成的各組成相幾何模型逐一隨機投放至指定區域，同時進行碰撞檢測判斷，直至各組成相的占比達到輸入的預期值。

步驟3：完成幾何結構建模，并對整個模型進行網格劃分，賦予各組成相力學參數及設置邊界條件等步驟。

步驟4：將模型提交計算，基于雙尺度方法進行后處理，輸出所期望的混凝土宏觀力學參數。

2混凝土數值模擬正交試驗設計

基于前述數值模擬方法，混凝土內部的多種因素都有可能對混凝土抗壓強度、彈性模量產生影響。正交試驗可以高效分析多因素多水平對混凝土抗壓強度、彈性模量的影響效應，正交試驗中設置各因素的原因如下。

1）粗骨料的面積分數（因素A）可以反映出實際混凝土配合比的改變對整體強度性能的影響，粗骨料占比的改變也就意味著砂漿及界面過渡區面積分數的相對改變。

2）混凝土內部的孔隙率（因素B）可以反映出實際混凝土中存在的初始缺陷對整體性能的影響，孔隙率衡量著混凝土中是否存在初始缺陷及初始缺陷大小。

3）粗骨料的種類（因素C）可以反映出實際混凝土中選用不同種類的粗骨料對整體力學性能的影響。

4）水泥砂漿的性能（因素D）可以反映出實際混凝土中的水泥砂漿采用不同的強度等級對整體力學性能的影響。

正交試驗采用了L（4）正交表，各因素與水平的設置如表4所示。其中，因素C和D涉及了不同水平的材料屬性，具體如表1—3所示。

3結果與討論

3.1混凝土數值模擬結果與試驗驗證

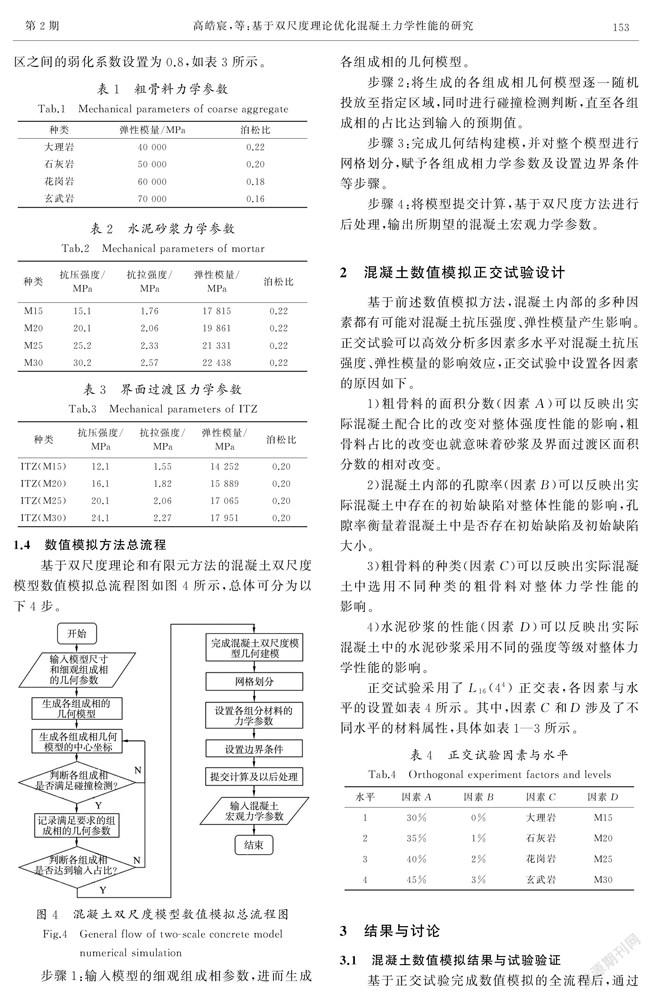
基于正交試驗完成數值模擬的全流程后，通過后處理得到的各工況下混凝土的應力-應變曲線如圖5所示。

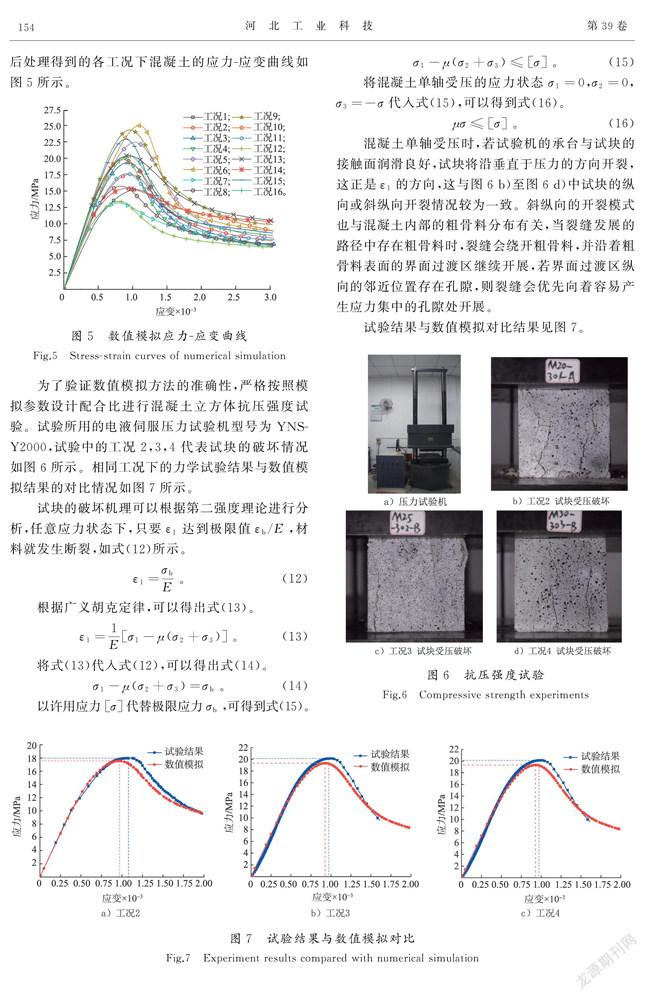
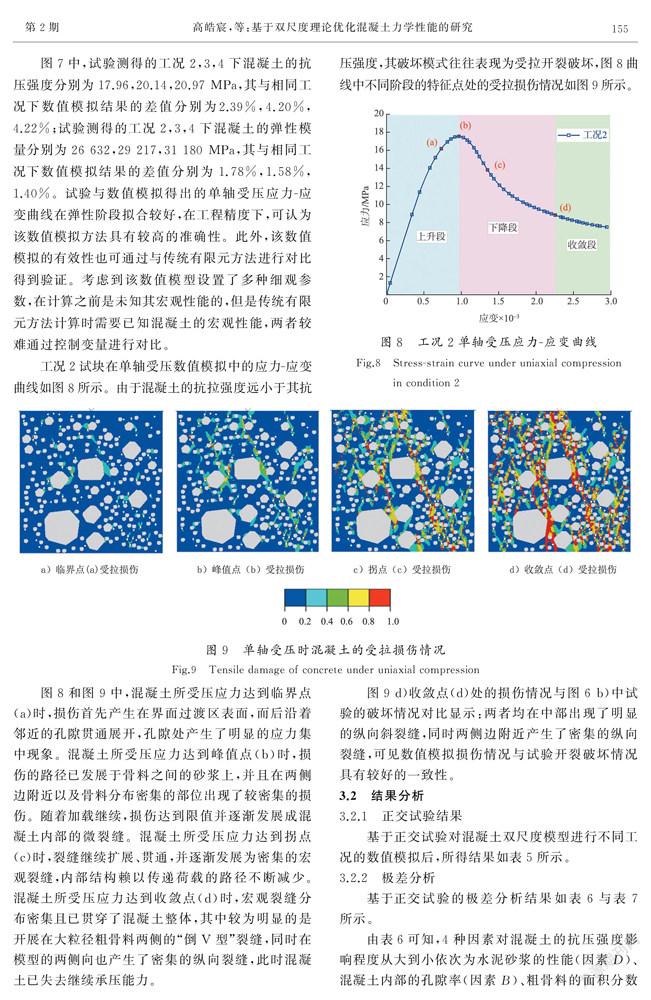
為了驗證數值模擬方法的準確性，嚴格按照模擬參數設計配合比進行混凝土立方體抗壓強度試驗。試驗所用的電液伺服壓力試驗機型號為YNS-Y2000，試驗中的工況2，3，4代表試塊的破壞情況如圖6所示。相同工況下的力學試驗結果與數值模擬結果的對比情況如圖7所示。

試塊的破壞機理可以根據第二強度理論進行分析，任意應力狀態下，只要ε達到極限值ε/E，材料就發生斷裂，如式（12）所示。

混凝土單軸受壓時，若試驗機的承臺與試塊的接觸面潤滑良好，試塊將沿垂直于壓力的方向開裂，這正是ε的方向，這與圖6 b）至圖6 d）中試塊的縱向或斜縱向開裂情況較為一致。斜縱向的開裂模式也與混凝土內部的粗骨料分布有關，當裂縫發展的路徑中存在粗骨料時，裂縫會繞開粗骨料，并沿著粗骨料表面的界面過渡區繼續開展，若界面過渡區縱向的鄰近位置存在孔隙，則裂縫會優先向著容易產生應力集中的孔隙處開展。

圖7中，試驗測得的工況2，3，4下混凝土的抗壓強度分別為17.96，20.14，20.97 MPa，其與相同工況下數值模擬結果的差值分別為2.39%，4.20%，4.22%;試驗測得的工況2，3，4下混凝土的彈性模量分別為26 632，29 217，31 180 MPa，其與相同工況下數值模擬結果的差值分別為1.78%，1.58%，1.40%。試驗與數值模擬得出的單軸受壓應力-應變曲線在彈性階段擬合較好，在工程精度下，可認為該數值模擬方法具有較高的準確性。此外，該數值模擬的有效性也可通過與傳統有限元方法進行對比得到驗證。考慮到該數值模型設置了多種細觀參數，在計算之前是未知其宏觀性能的，但是傳統有限元方法計算時需要已知混凝土的宏觀性能，兩者較難通過控制變量進行對比。

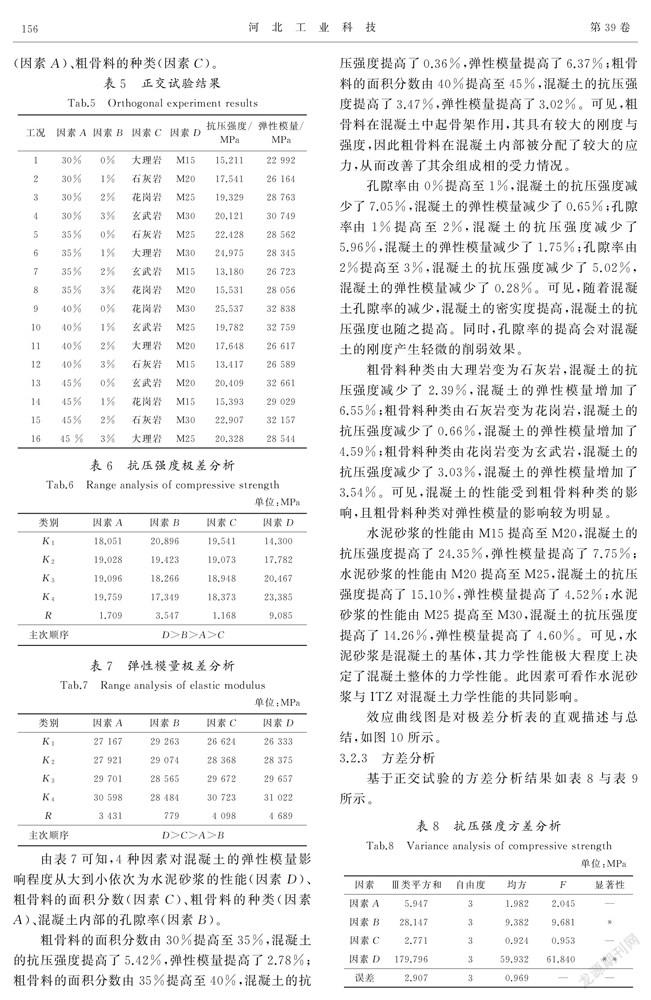
工況2試塊在單軸受壓數值模擬中的應力-應變曲線如圖8所示。由于混凝土的抗拉強度遠小于其抗壓強度，其破壞模式往往表現為受拉開裂破壞，[JP4]圖8曲線中不同階段的特征點處的受拉損傷情況如圖9所示。

圖8和圖9中，混凝土所受壓應力達到臨界點（a）時，損傷首先產生在界面過渡區表面，而后沿著鄰近的孔隙貫通展開，孔隙處產生了明顯的應力集中現象。混凝土所受壓應力達到峰值點（b）時，損傷的路徑已發展于骨料之間的砂漿上，并且在兩側邊附近以及骨料分布密集的部位出現了較密集的損傷。隨著加載繼續，損傷達到限值并逐漸發展成混凝土內部的微裂縫。混凝土所受壓應力達到拐點（c）時，裂縫繼續擴展、貫通，并逐漸發展為密集的宏觀裂縫，內部結構賴以傳遞荷載的路徑不斷減少。混凝土所受壓應力達到收斂點（d）時，宏觀裂縫分布密集且已貫穿了混凝土整體，其中較為明顯的是開展在大粒徑粗骨料兩側的“倒V型”裂縫，同時在模型的兩側向也產生了密集的縱向裂縫，此時混凝土已失去繼續承壓能力。

圖9 d）收斂點（d）處的損傷情況與圖6 b）中試驗的破壞情況對比顯示：兩者均在中部出現了明顯的縱向斜裂縫，同時兩側邊附近產生了密集的縱向裂縫，可見數值模擬損傷情況與試驗開裂破壞情況具有較好的一致性。

3.2結果分析

3.2.1正交試驗結果

基于正交試驗對混凝土雙尺度模型進行不同工況的數值模擬后，所得結果如表5所示。

3.2.2極差分析

基于正交試驗的極差分析結果如表6與表7所示。

由表6可知，4種因素對混凝土的抗壓強度影響程度從大到小依次為水泥砂漿的性能（因素D）、混凝土內部的孔隙率（因素B）、粗骨料的面積分數（因素A）、粗骨料的種類（因素C）。

由表7可知，4種因素對混凝土的彈性模量影響程度從大到小依次為水泥砂漿的性能（因素D）、粗骨料的面積分數（因素C）、粗骨料的種類（因素A）、混凝土內部的孔隙率（因素B）。

粗骨料的面積分數由30%提高至35%，混凝土的抗壓強度提高了5.42%，彈性模量提高了2.78%;粗骨料的面積分數由35%提高至40%，混凝土的抗壓強度提高了0.36%，彈性模量提高了6.37%;粗骨料的面積分數由40%提高至45%，混凝土的抗壓強度提高了3.47%，彈性模量提高了3.02%。可見，粗骨料在混凝土中起骨架作用，其具有較大的剛度與強度，因此粗骨料在混凝土內部被分配了較大的應力，從而改善了其余組成相的受力情況。

孔隙率由0%提高至1%，混凝土的抗壓強度減少了7.05%，混凝土的彈性模量減少了0.65%;孔隙率由1%提高至2%，混凝土的抗壓強度減少了5.96%，混凝土的彈性模量減少了1.75%;孔隙率由2%提高至3%，混凝土的抗壓強度減少了5.02%，混凝土的彈性模量減少了0.28%。可見，隨著混凝土孔隙率的減少，混凝土的密實度提高，混凝土的抗壓強度也隨之提高。同時，孔隙率的提高會對混凝土的剛度產生輕微的削弱效果。

粗骨料種類由大理巖變為石灰巖，混凝土的抗壓強度減少了2.39%，混凝土的彈性模量增加了6.55%;粗骨料種類由石灰巖變為花崗巖，混凝土的抗壓強度減少了0.66%，混凝土的彈性模量增加了4.59%;粗骨料種類由花崗巖變為玄武巖，混凝土的抗壓強度減少了3.03%，混凝土的彈性模量增加了3.54%。可見，混凝土的性能受到粗骨料種類的影響，且粗骨料種類對彈性模量的影響較為明顯。

水泥砂漿的性能由M15提高至M20，混凝土的抗壓強度提高了24.35%，彈性模量提高了7.75%;水泥砂漿的性能由M20提高至M25，混凝土的抗壓強度提高了15.10%，彈性模量提高了4.52%;水泥砂漿的性能由M25提高至M30，混凝土的抗壓強度提高了14.26%，彈性模量提高了4.60%。可見，水泥砂漿是混凝土的基體，其力學性能極大程度上決定了混凝土整體的力學性能。此因素可看作水泥砂漿與ITZ對混凝土力學性能的共同影響。

效應曲線圖是對極差分析表的直觀描述與總結，如圖10所示。

3.2.3方差分析

基于正交試驗的方差分析結果如表8與表9所示。

如表8所示，對于抗壓強度指標：水泥砂漿性能達到了高度顯著水平（α=0.01），孔隙率達到了顯著水平（α=0.05），粗骨料面積分數和粗骨料種類沒有達到顯著水平。

如表9所示，對于彈性模量指標：水泥砂漿性能達到了高度顯著水平（α=0.01），粗骨料種類達到了高度顯著水平（α=0.01），粗骨料面積分數達到了高度顯著水平（α=0.01），孔隙率沒有達到顯著水平。

4結語

將雙尺度理論作為理論基礎，通過有限元方法完成了混凝土雙尺度模型的數值模擬全過程，達到了對混凝土宏觀力學性能精細化計算與優化的目的，并基于數值模擬參數進行了混凝土立方體抗壓強度試驗來驗證模擬的準確性，結論如下。

1）基于混凝土雙尺度模型進行的數值模擬可以預測混凝土的宏觀力學性能。該方法已實現參數化、程序化，其參數可根據研究的需要進行靈活調整。

2）雙尺度理論和有限元方法首次被結合用于混凝土等效力學性能的精細化計算中，力學試驗結果證明該路徑可行。

3）混凝土的宏觀力學性能極大程度上受到細觀組成相的結構與性能的影響。粗骨料的作用更多在于增大混凝土剛度，其對抗壓強度的影響有限;砂漿的強度等級與混凝土的抗壓強度直接相關，砂漿性能決定了混凝土力學性能的上限;界面過渡區與孔隙是損傷與裂縫容易產生的部位，兩者決定了混凝土力學性能的下限。

目前混凝土中粗骨料的參數采用了線彈性本構關系，但實際中粗骨料是一種彈脆性材料，未來的精細化計算應該將粗骨料參數模擬為更加真實的本構關系。另外，目前雙尺度理論在混凝土數值模擬中的應用僅限于材料階段，未來雙尺度理論在混凝土數值模擬中的應用應向著結構階段發展。

參考文獻/References：

[1]WITTMANN F H，ROELFSTRA P E，SADOUKI HSimulation and analysis of composite structures[J].Materials Science and Engineering，1985，68（2）：239-248.

[2]劉光廷，王宗敏用隨機骨料模型數值模擬混凝土材料的斷裂[J].清華大學學報（自然科學版），1996，36（1）：84-89LIU Guangting，WANG ZongminNumerical simulation study of fracture of concrete materials using random aggregate model[J]. Journal of Tsinghua University （Science and Technology），1996，36（1）：84-89.

[3]馬懷發，陳厚群，黎保琨混凝土試件細觀結構的數值模擬[J].水利學報，2004，35（10）：27-35MA Huaifa，CHEN Houqun，LI BaokunMeso-structure numerical simulation of concrete specimens[J].Journal of Hydraulic Engineering，2004，35（10）：27-35.

[4]趙吉坤混凝土四相復合模型的三維細觀破壞模擬[J].土木建筑與環境工程，2009，31（4）：37-43ZHAO Jikun3D meso-scale failure simulation of four-phase composite concrete[J].Journal of Civil，Architectural & Environmental Engineering，2009，31（4）：37-43.

[5]宋來忠，廖大乾混凝土細觀結構的數值模擬研究[J].三峽大學學報（自然科學版），2018，40（6）：56-60SONG Laizhong，LIAO DaqianResearch on numerical simulation of meso-structure of concrete[J].Journal of China Three Gorges University（Natural Sciences），2018，40（6）：56-60.

[6]田夢云，張恩，曹瑞東，等基于細觀尺度的混凝土單軸力學性能仿真計算分析[J].應用力學學報，2020，37（3）：975-981TIAN Mengyun，ZHANG En，CAO Ruidong，et alMeso-scale simulation analysis of uniaxial mechanical behavior of concrete[J].Chinese Journal of Applied Mechanics，2020，37（3）：975-981.

[7]LI W，JIA Y J，LI L XA two-scale approach to numerically predict the strength and degradation of composites[J].Applied Composite Materials，2018，25（1）：85-103.

[8]王曉琴，楊名超，肖明，等自密實混凝土單軸壓縮試驗細觀模擬[J]中國科技論文，2020，15（12）：1410-1416WANG Xiaoqin，YANG Mingchao，XIAO Ming，et alMeso-scale simulation on uniaxial compression test of self-compacting concrete[J].China Sciencepaper，2020，15（12）：1410-1416.

[9]ERICSON C實時碰撞檢測算法技術[M].劉天慧譯北京：清華大學出版社，2010.

[10]陳青青，張煜航，張杰，等含孔隙混凝土二維細觀建模方法研究[J].應用數學和力學，2020，41（2）：182-194CHEN Qingqing，ZHANG Yuhang，ZHANG Jie，et al Study on a 2D mesoscopic modeling method for concrete with voids[J].Applied Mathematics and Mechanics，2020，41（2）：182-194.

[11]CHANDRA S，BERNTSSON LLightweight Aggregate Concrete Microstructure[M]. Norwich：William Andrew Publishing，2002.

[12]RAO G A，PRASAD B K PInfluence of type of aggregate and surface roughness on the interface fracture properties[J].Materials and Structures，2004，37（5）：328-334.

[13]CHEN Hongbing，XU Bin，WANG Jiang，et alParametric analysis on compressive strain rate effect of concrete usingmesoscale modeling approach[J].Construction and Building Materials，2020，246：118375.

[14]《工程地質手冊》編委會工程地質手冊[M].北京：中國建筑工業出版社，2007.

[15]杜修力，王陽，路德春水泥砂漿材料的靜動態應力應變關系研究[J].土木工程學報，2010，43（sup2）：119-126DU Xiuli，WANG Yang，LU DechunStudy on static and dynamic stress-strain relationship of cement mortar material[J].China Civil Engineering Journal，2010，43（sup2）：119-126.

[16]GB 175—2007通用硅酸鹽水泥[S].

[17]WRIGGERS P，MOFTAH S OMesoscale models for concrete：Homogenisation and damage behaviour[J].Finite Elements in Analysis and Design，2006，42（7）：623-636.

[18]ASBRIDGE A H，PAGE C L，PAGE M MEffects of metakaolin，water/binder ratio and interfacial transition zones on the microhardness of cement mortars[J].Cement and Concrete Research，2002，32（9）：1365-1369.

[19]LIAO Kuoyu，CHANG Pingkun，PENGA Y N，et alA study on characteristics of interfacial transition zone in concrete[J].Cement and Concrete Research，2004，34（6）：977-989.