距離最小化數據驅動計算方法中平衡因子取值影響研究

張玉輝，姜清輝

(武漢大學土木建筑工程學院，武漢 430072)

傳統彈性力學法求解邊值問題建立在聯立平衡微分方程、幾何方程以及物理方程的基礎上。其中平衡微分方程和幾何方程由靜力學平衡和運動學導出，無不確定性。而物理方程是在對觀測數據進行經驗總結和擬合的基礎上建立的，包括根據實驗數據識別現有模型參數，或者擬合提出一種新的材料物理模型，至今依舊是力學研究的熱點[1-3]，具有經驗性和不確定性。

距離最小化數據驅動計算方法是在大數據時代背景下由Kirchdoerfer 和Ortiz[4]首先提出，通過在應力-應變相空間內仿照應變能密度和應變余能密度的形式定義空間距離，在材料的宏觀力學響應數據庫內為每個積分點搜索并匹配最可能的應力-應變數據點。該方法在計算過程中不再依賴顯式表達式形式的材料本構關系，將聯立彈性力學三大方程的顯式求解問題轉變為搜索匹配最可能的靜力許可應力場、變形許可應變場和數據分配方案的最優化問題，最大程度上保留了觀測數據的原始性。各個搜索對象分別對應平衡微分方程約束下的可行解集、幾何方程約束下的可行解集和物理本構關系約束下的可行解子集。

針對數據點的質量，Kirchdoerfer 和Ortiz[5]在原有框架的基礎上，提出了熵最小化數據驅動計算方法，降低了數據噪音對計算精度的影響；針對邊值問題的類型，該方法的適用范圍被陸續推廣到動力學問題[6]、非線性彈性問題[7]以及非彈性問題[8]。在理論上，Conti 等[9]論證了該方法在數學層面上的一系列問題，Nguyen 等[10]給出了該方法在變分框架下的一般形式；在應用上，Yang 等[11]和Xu 等[12]將該方法與多尺度有限元法相結合，拓展了求解復合材料等效連續介質問題的新思路，Stainier 等[13]基于數字圖像關聯技術提出的數據識別方法能夠生成更有效的材料數據庫；在運行效率上，分層搜索方法[14]，k-d 樹搜索方法[15]的提出有效降低了計算開銷。

對比傳統彈性力學法，該計算方法除了以數據庫替換本構方程外，同時還要求輸入定義空間距離時使用的平衡參數。在一維桁架問題中，表現為一常數因子，記為C，用于平衡應力和應變單位上巨大的量級差；在平面和空間問題中表現為正定的常數矩陣，以保證距離度量始終為正，記為C，在平衡應力應變量綱的基礎上為各個方向上的分量也定義了權重。已發表的文獻多是針對數據庫容量[4-7,11-12]及數據點質量[5]對計算精度和運行效率的影響展開討論，對于平衡因子取值影響的討論卻很少，或是針對特定的模型和邊界條件，僅以計算結果的好壞給出取值建議[7,11-12]。

本文分別對線彈性桁架問題和線彈性平面問題中，平衡因子取值對算式的收斂速率和性能的影響進行了研究。結果表明：盡管平衡因子只是數值而沒有物理上的意義，不代表任何的材料力學響應，為保證計算精度，一定程度上仍需要反映材料自身的物理本構關系，這種依賴性將隨著數據點密度的上升而降低。

1 距離最小化數據驅動計算方法

上述整形約束二次規劃問題采用的求解策略是交替極小化算法。第一個極小化問題的描述為：從滿足物理本構關系的應力-應變場出發，找到相距最近的應力可行解和應變可行解；第二個極小化問題的描述為，從滿足力系平衡和幾何條件的應力-應變可行解出發，找到相距最近的應力-應變數據點。由此形成一個定點迭代過程：

式中：Zj表示第j步迭代中的數據點分配；PM表示子問題一向所有應力-應變可行解的集合(EL/KL)映射；PC表示子問題二向所有數據分配方案的集合(CL)映射。如圖1 所示。

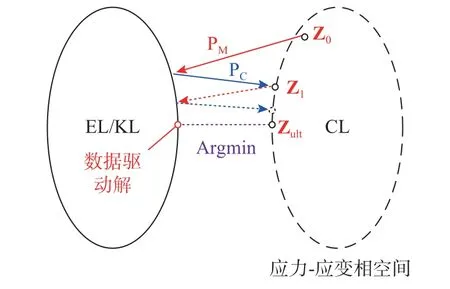
圖1 迭代流程Fig. 1 Iterative procedure

算法的目標在于，找到應力-應變相空間內，圖1 中兩個集合的交集或使二者距離取得最小值時的數據分配Zult。當Zj不再發生變化時，認為迭代收斂，滿足平衡和幾何約束條件的可行解輸出為力學邊值問題的近似解。輸入不同的迭代初值Z0、距離度量方式以及數據庫時，輸出的解不一定相同。

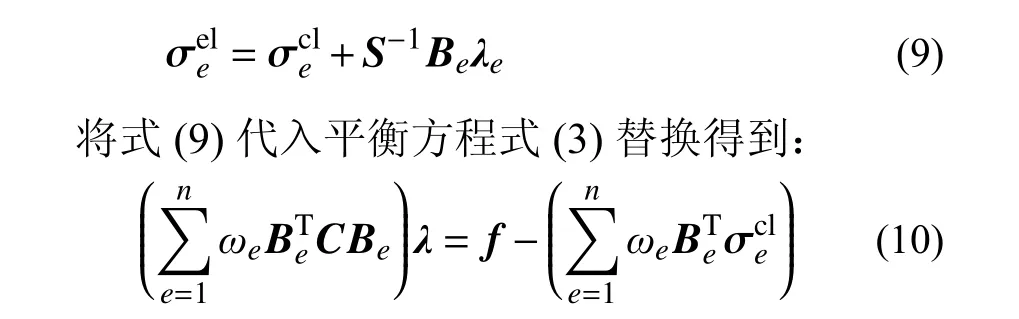
解線性方程式(8)和式(10)可得到節點位移列陣和拉格朗日乘子列陣，代入式(2)和式(9)即可得到應變可行解和應力可行解。

第二個極小化問題中約束條件式(2)、式(3)已滿足，只剩約束條件式(4)。有限元格式下，可以將問題分治到各個積分點，每個積分點均匹配最近的材料數據點時，全局罰函數最小，對應的數學模型為：

算法的本質是將碎片化后材料力學響應作為整形約束引入，從而找到滿足平衡方程和幾何方程，且與整形約束沖突程度最小的近似解。

2 桁架問題中常數C 的影響

文中使用的桁架和平面數據驅動計算程序均基于Visual Studio 19.0 平臺C++語言開發。

2.1 松弛問題的收斂速率

對收斂速率展開的分析建立在數據庫直接由材料宏觀力學特性表征的基礎上，即約束條件式(4)中去掉整形約束，數據庫替換為材料本構方程曲線：

式中，m=C/E為平衡常數與彈性模量的比例系數。

式(34)和式(35)表明，應力-應變可行解分別以恒定的收斂比線性收斂。以應力作軸，并將應變乘以彈性模量E投影到軸上，如圖2 所示。

圖2 桁架問題迭代過程Fig. 2 Iterative process of truss problem

當迭代步k趨于無窮時，應力-應變可行解都將收斂于精確解，而參數m只影響二者收斂的快慢。式(36)表明，分配的數據點始終位于該軸上應力和應變可行解之間，并最終恢復為有限元解。邊值條件對迭代路徑的影響主要體現在對可行解集合的限制，如靜定桁架結構的應力可行解始終保持為參考解(存在且只有一個靜力許可應力場)，在迭代過程中僅應變可行解發生改變。顯然，該類問題中平衡常數C的最優取值趨近于0，以加速應變解收斂。

2.2 原始問題的收斂性能

2.1 節中的討論基于數據點連續無間斷的假設，但是在實際情況中，數據點是離散且有限的，迭代過程不可能一直持續下去。該節主要討論數據庫為均勻分布的離散數據點時，平衡常數C對算式收斂性能的影響。恢復整形約束后的數據庫集合為：

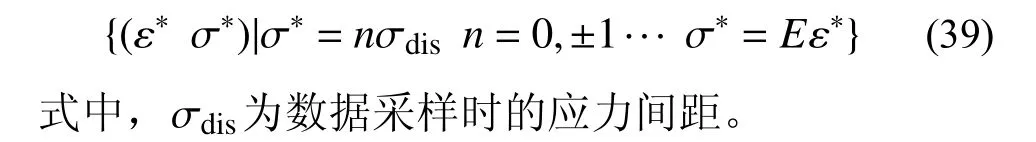
模型選用圖3(a)所示的代表性桁架[16]，位移約束和邊界荷載如圖所示，彈性模量E取10 MPa，兩桿橫截面面積取0.01 m2，荷載大小取3 kN，生成數據點的平均應力間距取10 kPa。平衡常數C取2×107時，對相同的迭代初值，松弛問題和原始問題對應的迭代路徑如圖3 所示。

對比圖3(b)及圖3(c)，當迭代步數較低時，二者路徑基本相同，但是在迭代末期，圖3(c)所示迭代過程在遠離參考解的位置收斂。這是由于原始問題中數據點作為整形約束，其間距限制了相鄰迭代步間數據點所能產生的最小改變量，形成了天然的收斂準則[17]。當自變量的變化不足以克服數據點間距時，算法將過早收斂。

以2.1 節松弛問題中應力-應變可行解的收斂速率聯立式(15)，應力數據在相鄰兩次迭代中的改變量計算如下：

2)數據點間距 σdis；給定迭代初值以及平衡常數后，應力-應變可行解將以恒定的收斂比線性收斂。迭代步數越多，收斂解的精度越高，這就要求數據點間距盡可能小。

3)系數m；式(40)表明，m=1 時，數據點的線性收斂比為50%；當m≠1 時，數據點的漸進線性收斂比將與應力-應變可行解中較大的一方相等(如圖3(b)中，m=2 時，應力可行解在第4 迭代步時已逼近參考解，此時數據點的收斂比與應變可行解一致)。當收斂階均為線性時，收斂比越大，收斂速率越慢，相鄰迭代步間自變量的變化量越小，越容易滿足停步準則，早熟收斂現象愈發顯著。

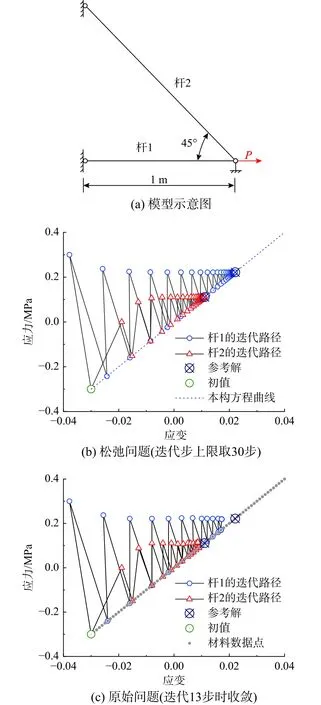
圖3 松弛問題和原始問題迭代路徑對比Fig. 3 Comparison of iterative paths between relaxation problem and original problem

從計算精度的角度看，當m＞1 時，經過充分迭代后，可以忽略應力項將式(42)改寫為：

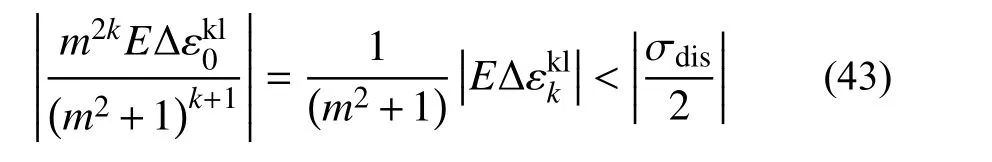
m越大，收斂時應變誤差越大；同理m＜1 時有：

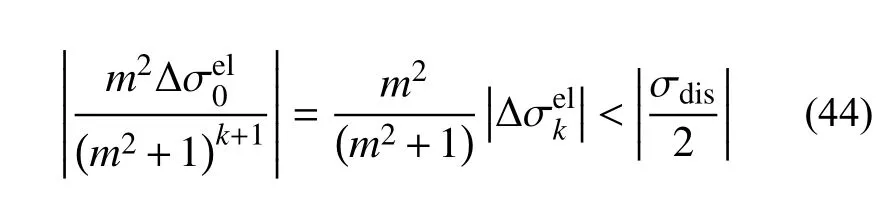
m越小，收斂時應力誤差越大；

本節分析表明，數據點的離散性將迭代步數k限制為有限的整數，這就要求C的取值能夠在有限的迭代步內，使應力-應變可行解均充分收斂至參考解鄰域。當m等于1 時，應力-應變解均以50%的收斂比線性收斂，二者相對精度不易產生較大差異。同時，數據點的漸進線性收斂比最小，迭代早熟收斂的可能性低，收斂解的可靠性高。當然，也可以根據實際工程中位移場和應力場計算精度需求和主要的邊界約束類型等靈活取值。

3 平面問題中矩陣C 的影響

對于平面問題，平衡系數從一個增加到九個，若按照對稱正定的要求給出系數矩陣C，剩余六個獨立參數。

3.1 松弛問題的收斂速率

從3.2 節生成的數據庫(數據庫A)中隨機選取初始數據分配方案Zini，然后，將其固定為每次試驗的迭代初值。將D中的每個元素分別乘上0 到2 的隨機系數，從而生成50 組滿足正定對稱約束的系數矩陣C用于試驗。為減輕量級變化帶來的影響，各矩陣均放縮至與D的二范數相等。圖5給出了第5 和第10 迭代步中，勢能和余能隨r變化的散點圖和擬合趨勢。

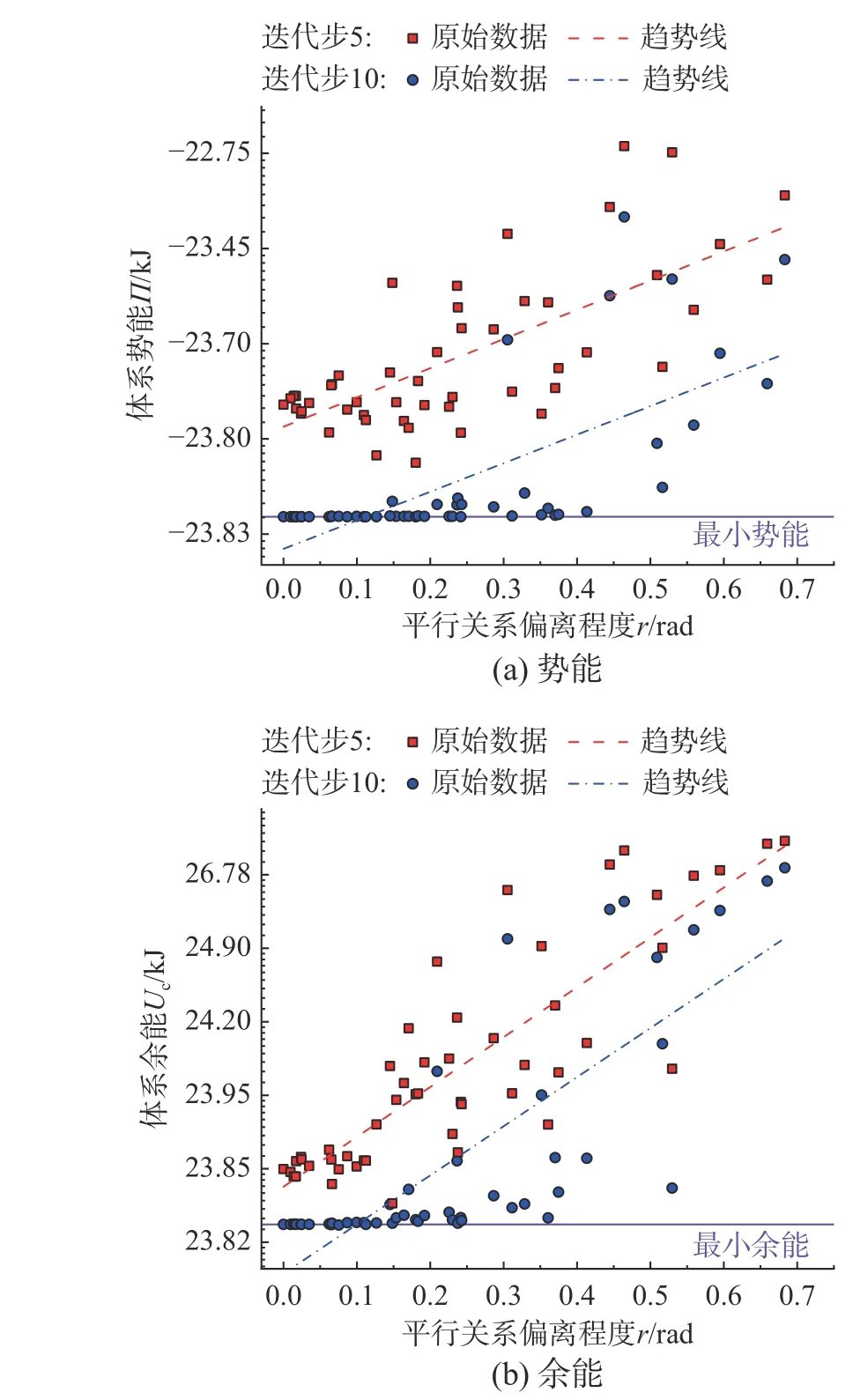
圖5 第5 和第10 迭代步的勢能和余能Fig. 5 Potential energy and complementary energy for thefifth and tenth iteration steps

從擬合趨勢上不難看出，隨r上升，勢能和余能均呈上升趨勢，這意味著算式收斂到精確解將需要更長的迭代步。至此，發現與m對應力-應變可行解收斂速率影響相反所不同的是，隨r的增大，以余能和勢能度量的應力-應變解整體收斂速率呈下降趨勢。

3.2 原始問題的收斂性能

為討論當數據庫為有限的離散數據點時，r對收斂性能的影響，構建了如下數據庫：離散數據點在域內均勻分布，應力數據取值的上下限為有限元參考解最大應力水平的1.2 倍。每個獨立的應力分量上均勻布置有20 個采樣點，正交組合后共生成8000 個數據點。在生成數據庫的過程中，應變數據直接由應力數據和給定的材料物理方程獲取。生成的數據庫記為數據庫A，其在應力空間內的投影如圖6 所示。

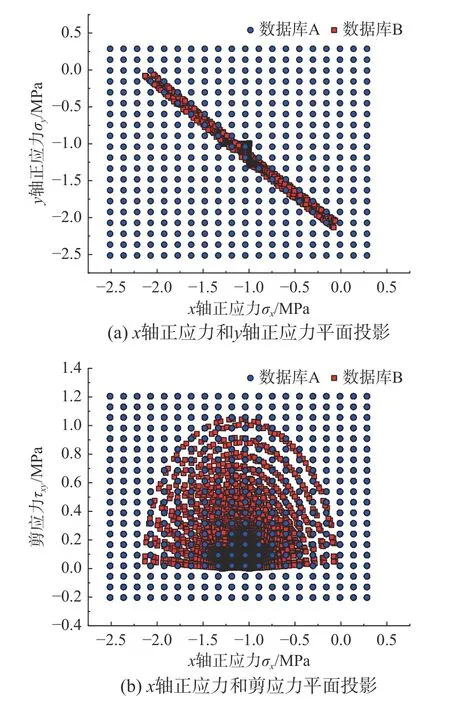
圖6 數據庫平面投影Fig. 6 Plane projection of database

第一節中指出算法的本質是找到滿足平衡方程和幾何方程，且與整形約束沖突程度最小的近似解。引入罰函數的數學意義是對數據點整形約束的放松，松弛后將形成以各個數據點為中心的凸包，但整個數據庫松弛后仍然是非凸集合。凸包的形態決定了跳出局部最優的難度，尖銳部分越有可能成為局部陷阱，“捕獲”迭代過程從而導致算法在局部極小值處收斂，如圖7 所示。

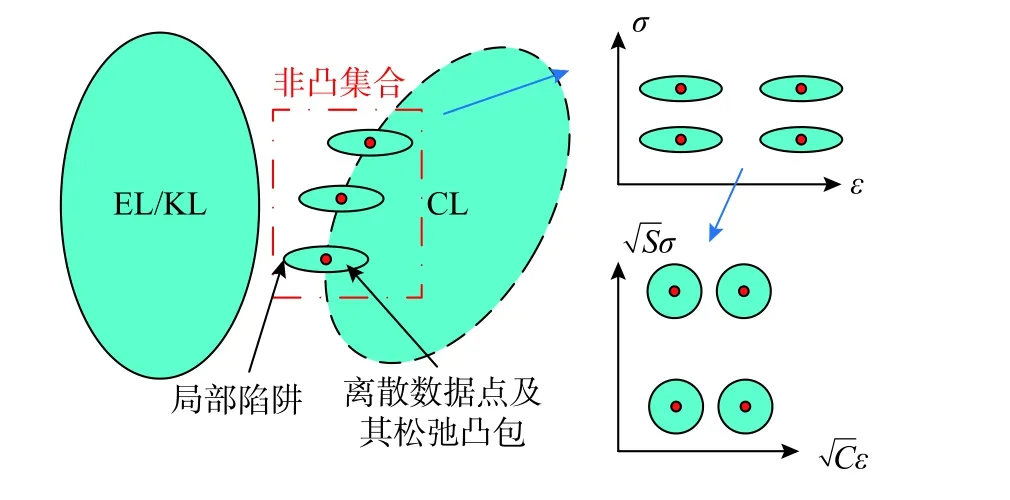
圖7 局部陷阱和自定義歐氏空間圖示Fig. 7 Visual illustration of local trap and custom Euclidean space

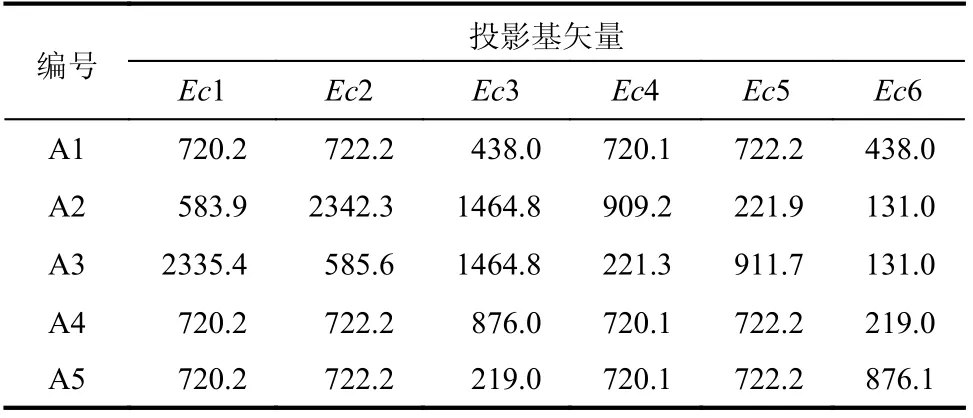
表1 基矢量方向上的方差Table 1 Variance in direction of basis vector

圖8 為Zini作為迭代初值時，應力數據的各個獨立分量與參考解的偏差絕對值統計直方圖。結果表明，方差越大的矢量方向上，收斂點的偏差幅度也越大。原因是方差一定程度上反映了給定數據庫在定義的歐氏空間內平均間距的大小，而在平均間距較大的矢量方向上，圖7 所展示的局部陷阱問題越嚴重。A1～A5 中的六個正交基矢量與應力-應變空間內相應分量之間的最大夾角不超過6°，在后續分析中近似為平行處理。

在試驗A2 中，數據庫A 在Ec2 和Ec3 基矢量方向上的方差最大，反映在計算結果(圖8(b)和圖8(c))中就是σy和τxy分量的偏差幅度最大；A3 的試驗現象與A2 類似；在試驗A4 和A5 中，數據庫A 分別在Ec3 和Ec6 基矢量方向上的方差最大，但是由于應力-應變數據是共同參與迭代的，因此，τxy分量的偏差幅度均增大。

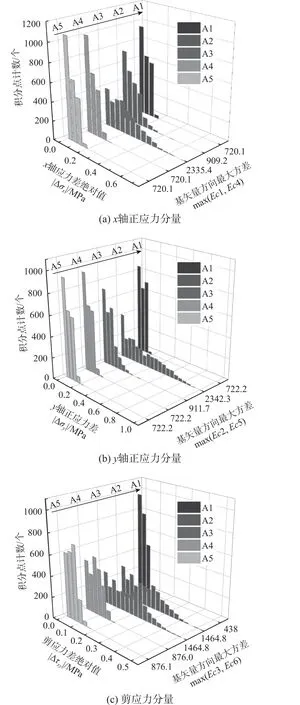
圖8 分配的數據點各應力分量與參考解之差Fig. 8 Difference of each stress component between assigned data point and reference solution

圖9 為某代表性積分點的應力數據在松弛問題和原始問題內的迭代路徑對比。其中標號C11=4C22對應試驗A2，標號C11=2C22則是在A2 的基礎上降低了r。在松弛問題中，C11=C22對照組仍沿直線路徑逼近精確解，各個分量的線性收斂比均為50%。隨C11/C22上升，σy和τxy分量收斂到參考解鄰域所需迭代步數顯著上升。從原始問題的迭代路徑觀察到，數據點在σx分量上均收斂至參考解鄰域，但在σy和τxy分量上，隨著C11/C22上升，與參考解的偏差幅度也相應上升。

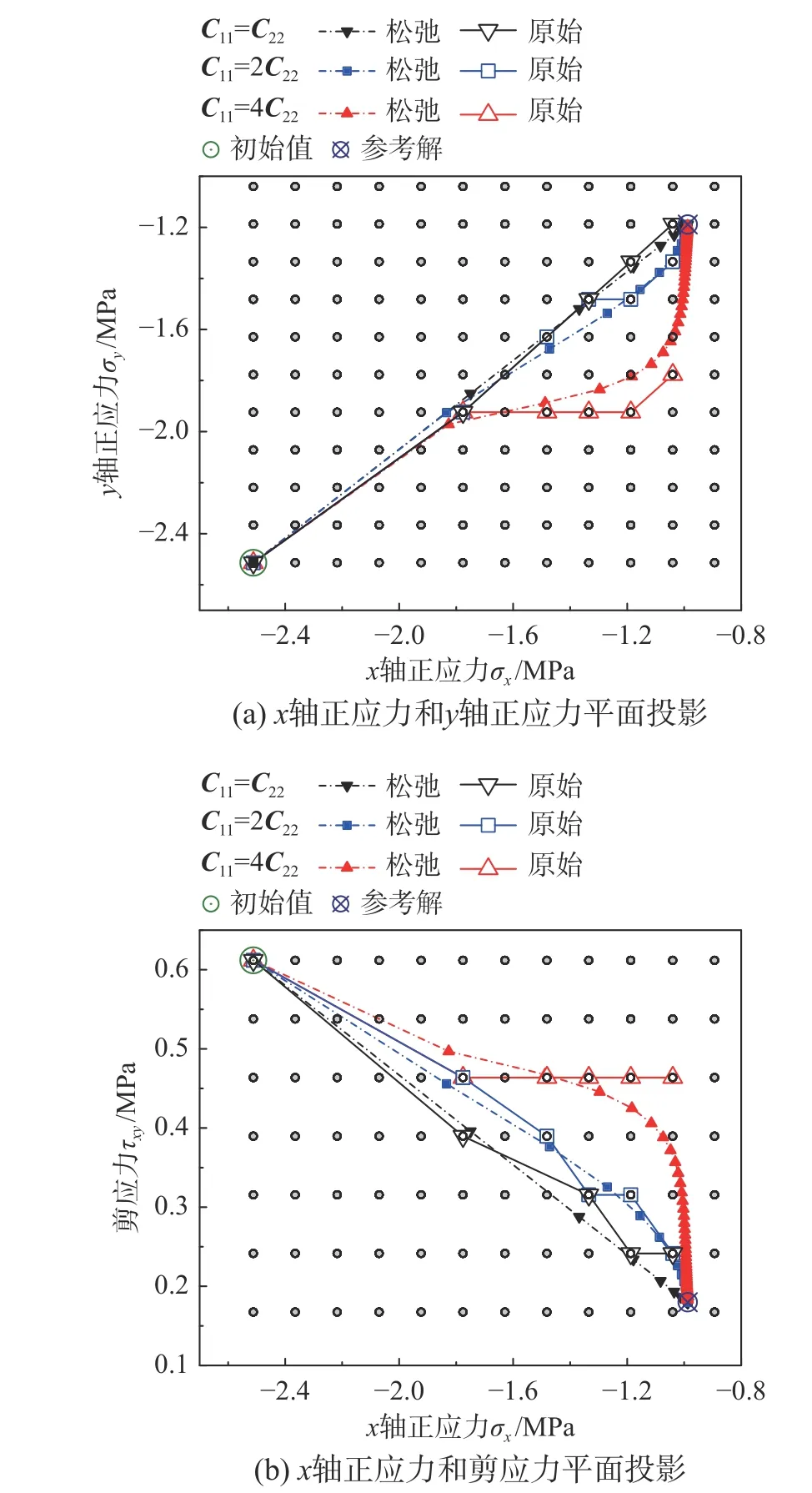
圖9 某代表性積分點的應力數據迭代路徑Fig. 9 Iterative path of stress data at a representative integral point

為進一步說明早熟收斂性質的影響，由圖4 中相同邊界條件但網格剖分更精細的有限元模型計算生成了第二個數據庫。共包含8044 個數據點，記為數據庫B，其在應力空間內的投影見圖6。

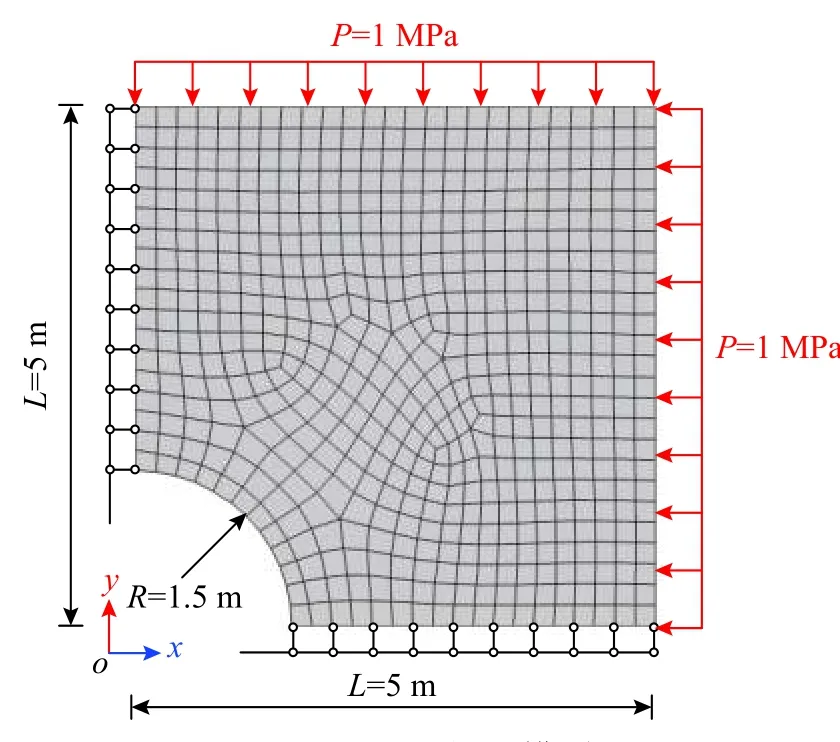
圖4 平面問題模型Fig. 4 Model of plane problem

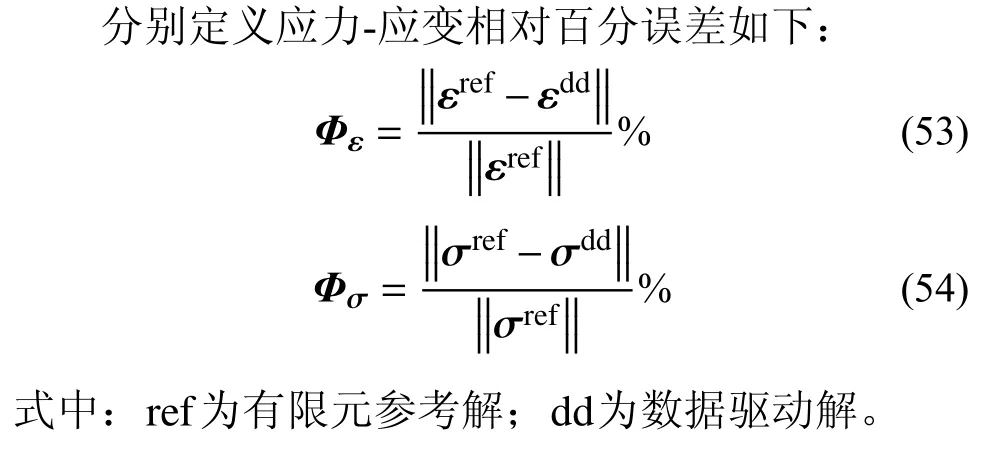
圖10 為使用不同數據庫驅動仿真計算時，各積分點的應力-應變相對誤差統計直方圖，計算過程中平衡因子取值均為D。分析表明：精確解附近的數據點密度比數據庫容量對算式精度的影響更大。從圖10 中可以看出，雖然數據庫容量相近，但使用數據庫B 的計算誤差明顯低于數據庫A。一方面，由于精確解附近的可行解集合被拓展，可能引入了新的全局最優解；另一方面，停步準則中允許出現更小的改變量，減小了在迭代過程中跳出局部最優的難度。合并兩個數據庫后，計算誤差仍與單獨使用數據庫B 相近，說明結合松弛問題在迭代末期、參考解鄰域內的性質來評價原始問題的收斂性能是有效可行的。

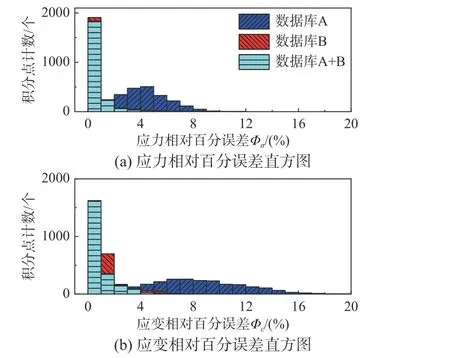
圖10 積分點誤差統計Fig. 10 Error statistics of integral points

4 結論

在線彈性距離最小化數據驅動算法的框架下，分別以桁架和平面問題為例，討論了平衡因子取值關于彈性常數的量級m和平行關系偏離程度r對算法的收斂速率及收斂性能的影響：

(1)在去掉整形約束的松弛問題中，對于給定的m，應力可行解和應變可行解分別以1/(1+m2)和m2/(1+m2)的收斂比線性收斂，并在迭代終止時作為近似解輸出。m越大于1，應力解的相對精度更高，m越小于1，應變解的相對精度更高。隨r的增大，以余能和勢能度量的應力-應變可行解整體收斂速率均呈下降趨勢。

(2)在包含整型約束的原始問題中，迭代路徑與松弛問題的主要區別在于：應力-應變數據點在相鄰迭代步間的最小改變量受整型約束限制，算法早熟收斂。r為0 時，應力-應變數據點沿直線逼近參考解，m取1 時的漸進線性收斂比最小，為50%；r不為0 時，數據點在各個分量方向上收斂到參考解鄰域所需的迭代步長出現較大差異。對于收斂較慢的分量，迭代終止時偏差幅度上升，早熟收斂問題愈發突出。

(3)除了m和r外，邊值約束條件的主要類型、隨機初值的選取、數據點間距也是影響算法收斂性能的因素。其中，精確解附近的數據點密度能夠很好解決數據點間距和平衡因子取值帶來的早熟收斂問題，從而保障算法的計算精度。