微波超視距雷達組網探測范圍研究

湯華濤 察豪 田斌 王彬彬

（海軍工程大學電子工程學院，武漢 430033）

引 言

微波超視距雷達是一種常用的對海探測雷達，在蒸發波導條件下，該雷達可實現超視距探測，即對艦船目標的探測距離大于視距. 為了評估微波超視距雷達的探測效能，以提供準確的信息保障服務，必須根據波導條件實時估計其對艦船目標的探測范圍.然而，超視距探測時雷達對艦船目標探測距離的估計不同于視距，傳統的雷達方程已不再適用，需考慮蒸發波導條件下傳播因子的變化情況[1]. 同時，隨著雷達裝備的發展，構建以網絡中心為主的雷達組網已成為必然趨勢，通過雷達組網，可以在不改變現有裝備性能的前提下，經過不同的組織形式來提高雷達的遠距離探測、反隱身和抗干擾能力[2]. 因此，研究微波超視距雷達組網狀態下對艦船目標的探測范圍具有重要的軍事意義.

微波超視距雷達探測目標時電磁波不再是直線傳播，在目標處不同高度上的入射波傳播因子不同，即目標處入射波的強度與高度有關. 在考慮傳播因子的基礎上，文獻[3-4]通過求解電磁波傳播的拋物方程，得到了蒸發波導條件下雷達作用距離的一種估計方法. 文獻[5-8]也做了類似的工作. 但是，以上研究沒有考慮目標雷達散射截面(radar cross section,RCS)在方位角上的起伏，都假設目標RCS 周向均勻分布，且研究對象為單部雷達.

通常情況下，艦船目標RCS 隨方位角的變化起伏很大，不考慮目標RCS 起伏得到的探測距離估計會與實際探測距離有所差異；同時，當雷達組網時，不同雷達對目標的觀測角度不同，得到的探測距離估計也不相同，多部雷達互補后得到的探測距離估計也將不同于單部雷達. 本文在蒸發波導傳播特性研究的基礎上，同時考慮艦船目標RCS 在高度和方位角上的分布，建立雷達組網時對艦船目標的探測范圍評估模型，分析雷達組網對艦船目標探測范圍的影響.

1 蒸發波導傳播因子估計

式中：F 和F-1分別表示傅里葉變換及傅里葉反變換因子；p=ksina，a為傳輸角.

2 艦船目標最大探測距離計算

任何目標的RCS 值都會隨探測方位角的不同而產生劇烈的變化[2]. 為了得到艦船目標RCS 隨方位角的變化情況，可利用仿真軟件建立艦船的三維幾何模型，然后計算其周向RCS，也可以通過實驗測試得到艦船目標不同角度RCS 值σθ，觀測方位角為θ.而對于目標RCS 在高度上的分布，與其相關的研究較少，目前還沒有成熟的理論成果[9-10]. 根據參考文獻[11]，可假設艦船目標RCS 在垂直高度上的分布服從高斯分布，且其分布密度函數為p(z)，設目標高度為h，將目標在高度上劃分為N等份，若N取值較大，每等份可近似作為點目標處理，則可得到高度為nΔz(n=0,1,2,···,N-1)的部分RCS 為

式中：Pr和Pt的單位均為dBW；G、Ls、L(R)的單位為dB；λ 的單位為m；σθ的單位為m2.

設雷達接收機靈敏度為Stmin，當Pr=Stmin時，可計算得到Rθ=Rmax，即得到觀測方位角為θ 時雷達對艦船目標的最大探測距離Rθ.

3 雷達網探測范圍評估模型

設有M部雷達組成雷達網，雷達網中有一部雷達探測到目標即視為雷達網探測到目標. 以某部雷達為坐標原點，建立直角坐標系，如圖1 所示，則其他雷達的坐標為 (xi,yi)(i=2,3,4,···,M). 假設與x軸夾角為 φ的方向上有一個目標，且軸線與正北方向夾角為φ，目標到原點的距離為d，則雷達網評估模型詳細步驟如下：

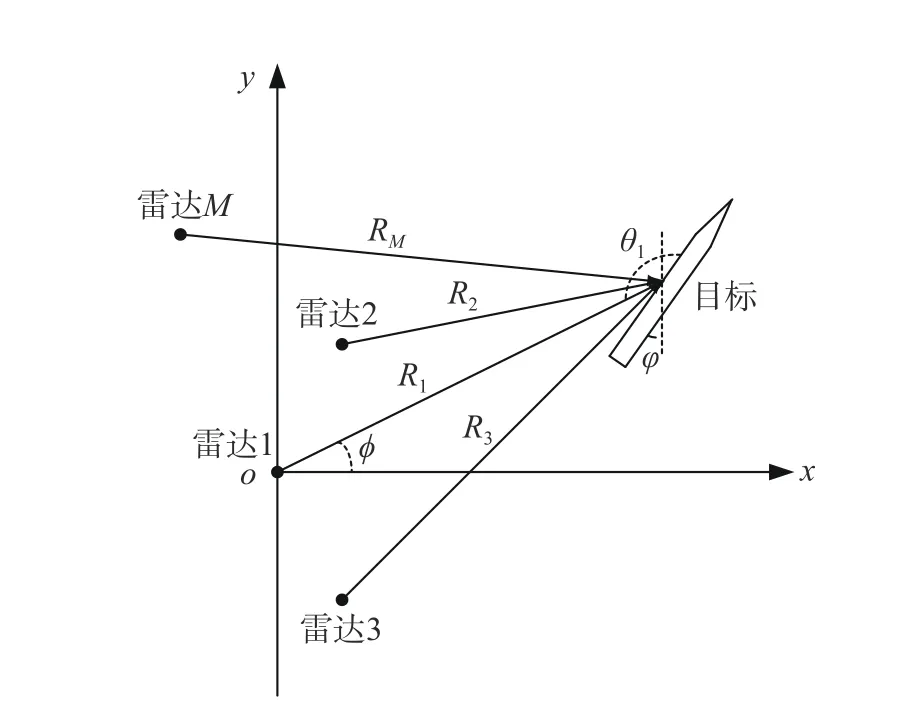
圖1 雷達組網探測示意圖Fig. 1 Diagram of detection radar network

1)計算雷達網各雷達對目標的觀測距離和觀測角：

上述評估模型同時考慮了蒸發波導和雷達組網對目標探測距離的影響，將目標RCS 按高度和方位角分布描述，并將雷達網對目標的全周向最大探測疊加，最終得到了雷達網對目標的探測范圍. 值得注意的是，本文在計算雷達網 φ方向上的目標最大探測距離時，采用的判定條件是目標自身姿態角φ 在0～359°的任何角度上(分辨率為1°)，雷達網都能探測到目標，與傳統的最大探測距離計算方法有所不同.

4 仿真分析

以某艦船為研究對象，其RCS 隨方位角起伏較大，在左右舷約90°及艦尾方向存在極大值，對目標總體RCS 貢獻較大，RCS 最大值為1.12×106m2，平均值為5.4×104m2. 蒸發波導高度12 m.

設由三部岸基微波超視距雷達組成雷達網，從南到北依次布設，坐標分別為雷達1(0，0)、雷達2(5，10)、雷達3(5，-10)(單位為km)，監視東面海域艦船目標，雷達1 所在的y軸為海岸線. 三部雷達參數相同，設置檢測概率90%、虛警概率10-6.

4.1 假設艦船目標的航行姿態未知

此時目標的軸線與正北方向夾角未知，認為雷達對目標的觀測角可能為任意角度，利用文獻[2]中的方法單獨計算各雷達對目標的最大探測距離為79 km，并將探測范圍相互疊加，與本文中雷達組網時的方法計算結果做對比，結果如圖2 所示.

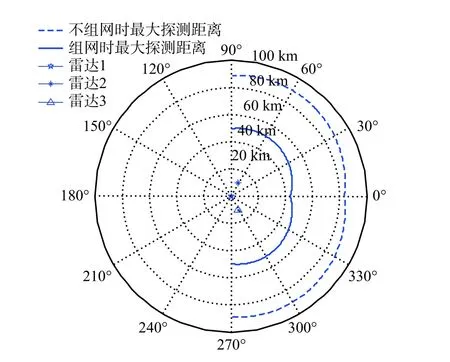
圖2 目標航行姿態未知時的有效探測范圍Fig. 2 Effective maximum detection range of unknown navigation attitude

圖2 中，雷達不組網時，各雷達探測范圍相互疊加后最大探測距離大約為90 km；雷達組網時的探測范圍反而比不組網時小，最大探測距離約為50 km.但事實上，文獻[2]中在計算各雷達對目標的最大探測距離時，采用的是目標平均RCS，由于目標RCS 在方位角上的起伏特性，目標各方位角上RCS 大于平均RCS 的占比為19%，即用文獻[2]中的方法計算得到的結果準確率為19%，當目標的航行姿態未知時，雷達對目標的最大探測距離有81%的概率達不到90 km. 而本文算法得到的最大探測距離為最大有效探測距離，即目標的航行姿態未知時，雷達網對目標的最大探測距離至少為50 km. 為了研究雷達組網對目標最大探測距離的影響，使用本文第3 節建立的雷達網評估模型時，在第2 步、3 步中，若全部Pri＜Stmin，并不立即進入第4 步，而是繼續以1°的步長增加φ 直至φ+359°；若在φ+1°～φ+359°的所有角度上，存在Pri=Stmin的占比大于等于19%，則進入第5步，否則進入第4 步. 使用更改后的雷達網評估模型計算準確率為19%時的最大探測距離如圖3所示.

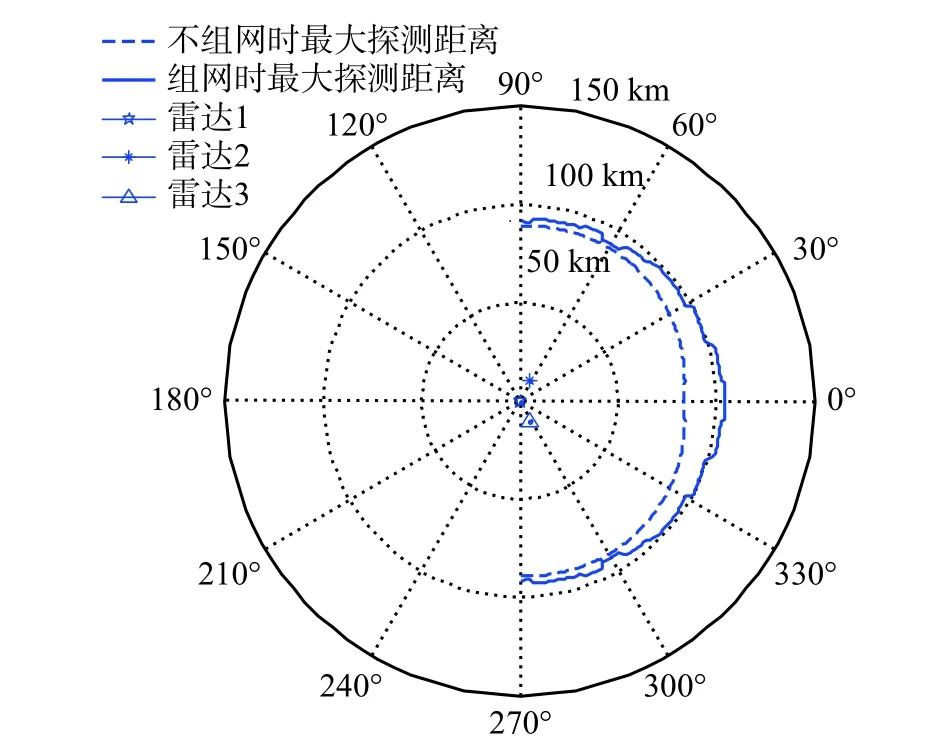
圖3 目標航行姿態未知時的探測范圍Fig. 3 Maximum detection range of unknown navigation attitude

圖3 中，雷達組網對目標的探測范圍為一段折線形成的包絡面，該探測范圍與不組網時相比增大了約11.20%；折線最遠處距離雷達1 約105 km，處于雷達網的正東面，與不組網相比增大了約16.67%. 由于目標部分角度的RCS 較大，雷達組網后各雷達對目標的觀測角度不同，探測距離相互補充，增大了對目標的探測范圍.

4.2 假設艦船目標由南向北航行

此時目標的軸線與正北方向夾角為0°，雷達網對目標的觀測范圍以左舷為主，利用本文方法計算雷達網對目標的有效探測范圍，結果如圖4 所示.

圖4 中，雷達網對目標的有效探測范圍最大值約130 km，最小值約50 km. 由于目標左右舷約90°及艦尾方向RCS 較大，當目標處于雷達網南面時，雷達網對目標的觀測方向以艦艏為主，最大探測距離較小；當目標處于雷達網北面時，雷達網對目標的觀測方向以艦尾為主，最大探測距離較大；當目標處于雷達網東面時，雷達網對目標的觀測方向以左舷為主，最大探測距離最大.

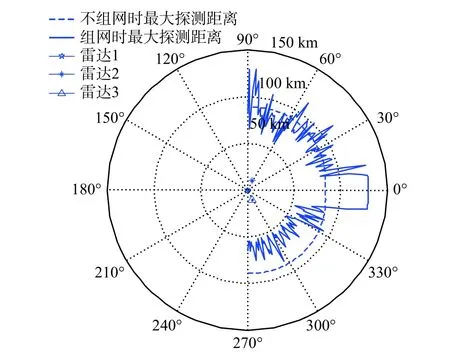
圖4 目標由南向北航行時的有效探測范圍Fig. 4 The effective maximum detection range of the target sailing from south to north

4.3 假設艦船目標由東向西航行

此時目標的軸線與正北方向夾角為90°，雷達網對目標的觀測范圍以艦艏為主，利用本文方法計算雷達網對目標的有效探測范圍，結果如圖5 所示.

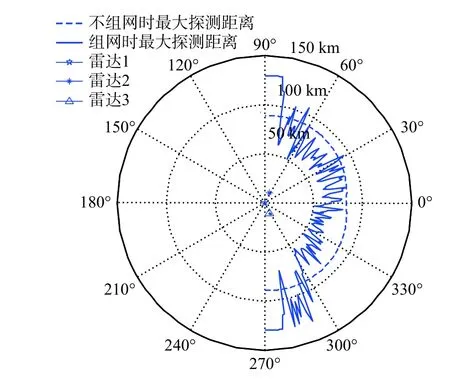
圖5 目標由東向西航行時的有效探測范圍Fig. 5 The effective maximum detection range of the target sailing from east to west

圖5 中，雷達網對目標的有效探測范圍最大值約128 km，最小值約50 km，且在大部分方位上小于90 km. 目標艦艏方向RCS 較小，當其由東向西航行時，雷達網對其有效探測距離較小.

5 結 論

蒸發波導條件下，目標處入射波的強度與高度有關，學者們研究了目標RCS 在高度上的分布對微波超視距雷達最大探測距離的影響，并建立了最大探測距離評估模型. 本文在此基礎上，考慮目標RCS在方位角上的分布，建立了雷達組網時的探測范圍評估模型，計算了三種不同情形下雷達組網后的探測范圍，并通過與不組網時的評估模型相對比得出以下結論：

1)當目標運動姿態未知且兩種評估模型的準確率相同時，雷達組網增大了雷達的探測范圍. 具體而言，雷達組網使雷達的探測范圍增加了11.20%，在特定方向上使探測距離增加了16.67%.

2)當目標運動姿態已知時，在極大提高評估結果準確性的前提下，雷達組網在部分方位角上增大了最大探測距離，同時在部分方位角上減小了最大探測距離. 從探測范圍的角度證明了雷達組網的可行性和優越性，為微波超視距雷達的組網使用提供了理論支撐.

本文使用的艦船目標RCS 高度分布模型較為粗糙，下一步應著重研究艦船目標RCS 在蒸發波導條件下隨高度分布的規律，建立更為精確的高度分布模型，進而提高微波超視距雷達組網探測范圍評估模型的準確性.